Продолжение определения синуса, косинуса, тангенса и котангенса

1.

2.

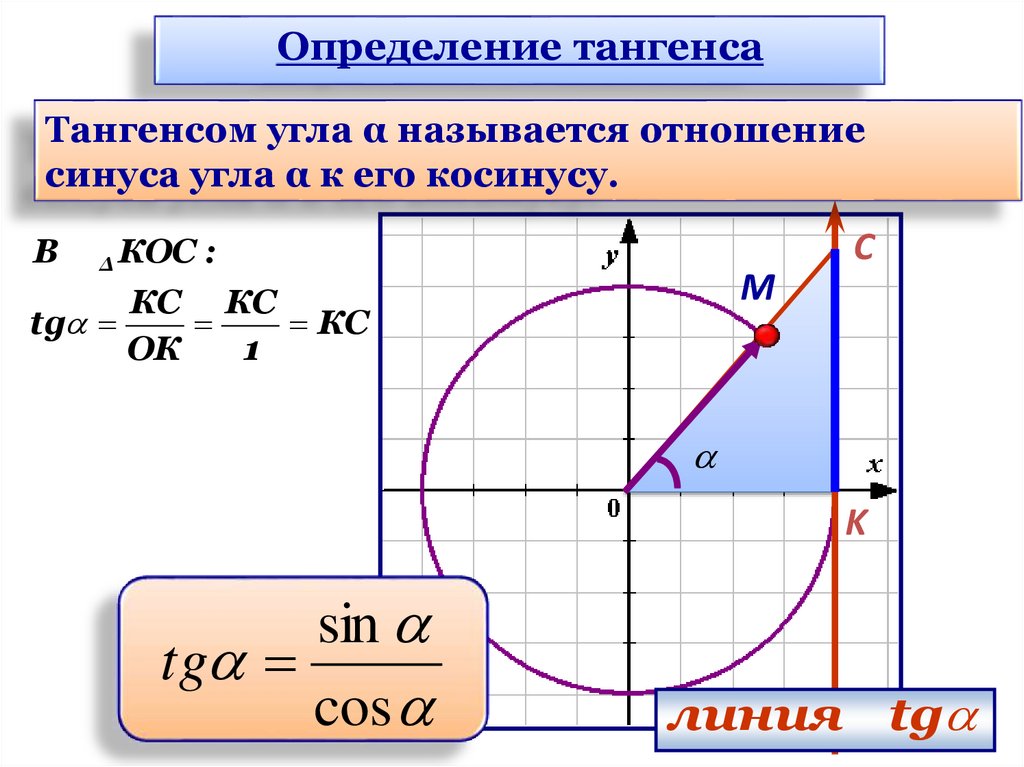
Определение тангенса
Тангенсом угла α называется отношение
синуса угла α к его косинусу.
В
Δ
C
КОС :
M
КС КС
tg
КС
ОК
1
K
sin
tg
cos
линия tg

3.

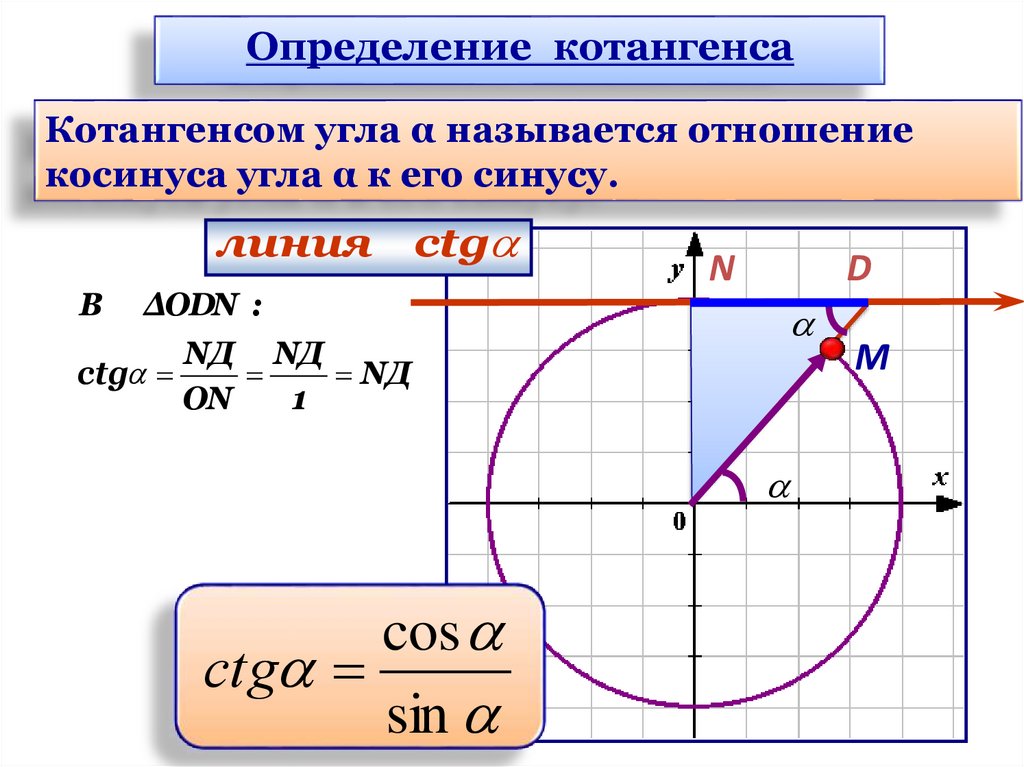
Определение котангенса
Котангенсом угла α называется отношение
косинуса угла α к его синусу.
линия сtg
В
ΔODN :
NД NД
ctg
NД
ОN
1
N
D
cos
сtg
sin
M

4.

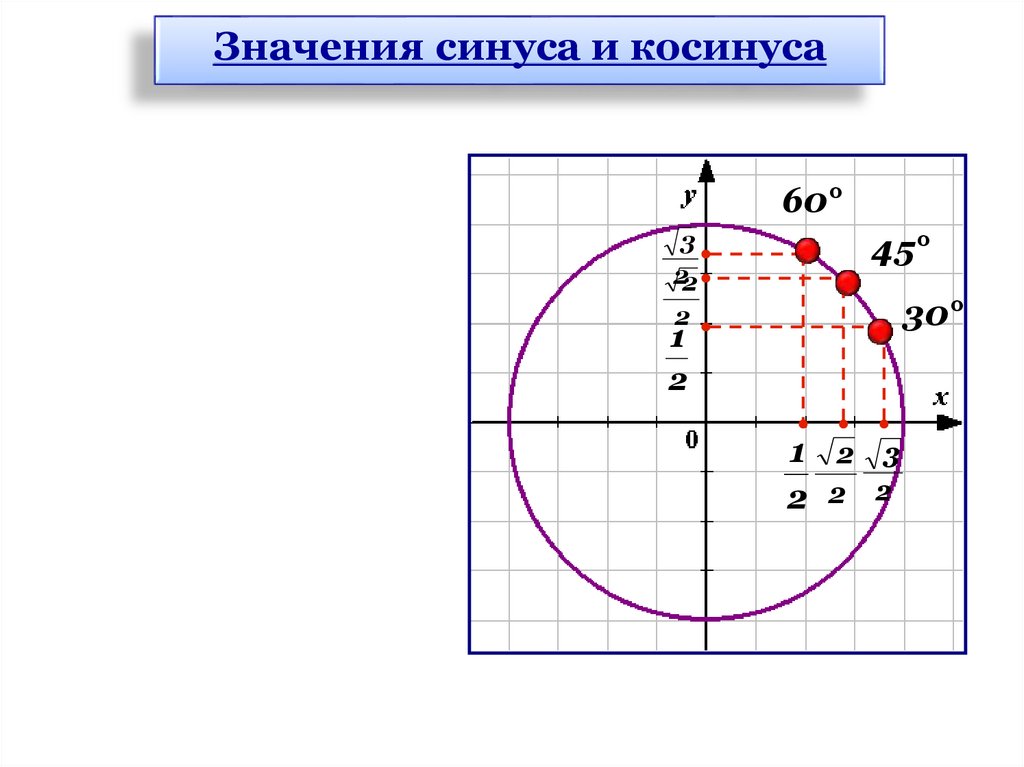
Значения синуса и косинуса
60°
3
22
45°
30°
2
1
2
1 2 3
2 2 2

5.

6.

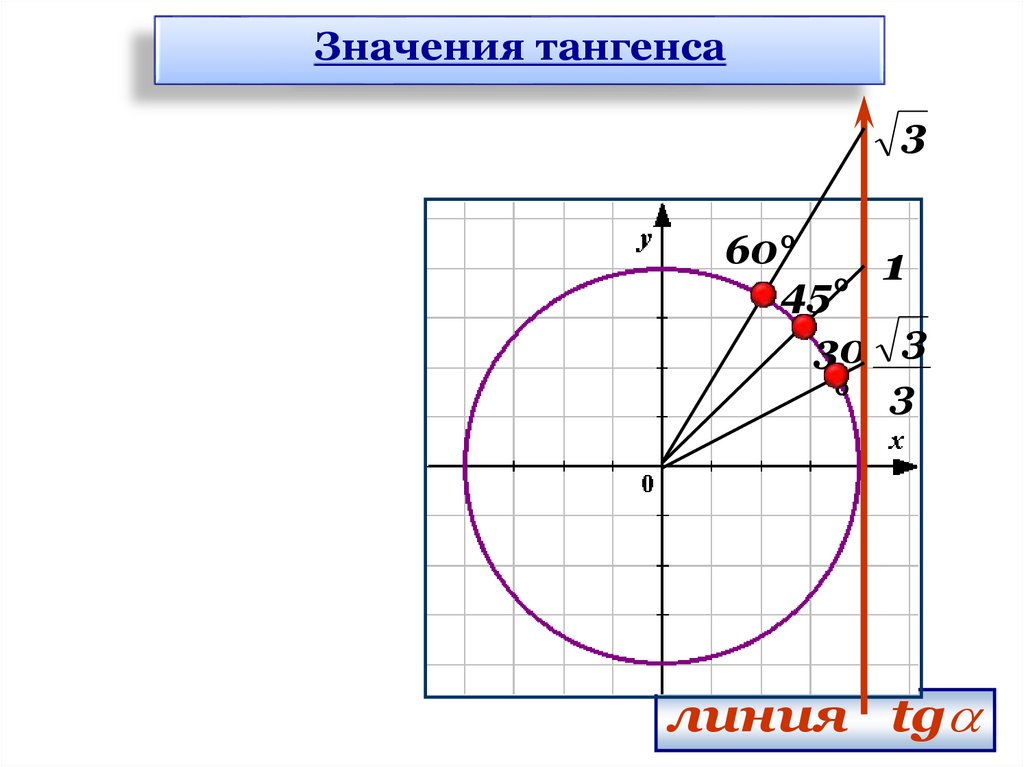
Значения тангенса
3
60°
1
45°
30 3
° 3
линия tg

7.

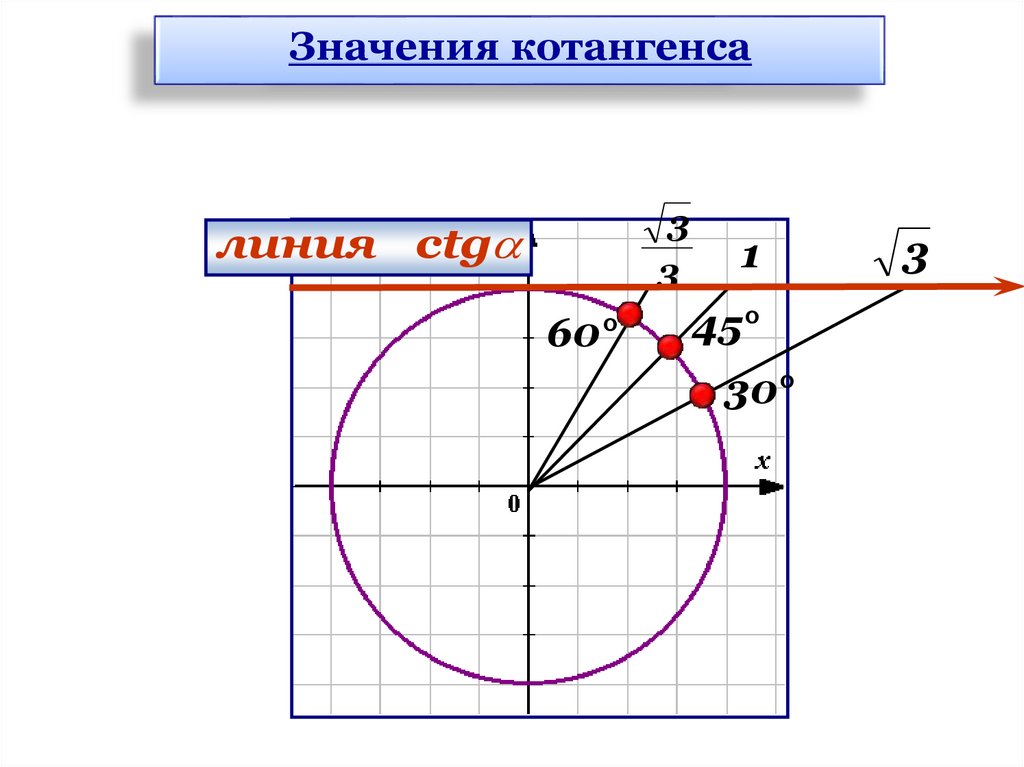
Значения котангенса
3
3
линия сtg
60°
1
45°
30°
3

8.

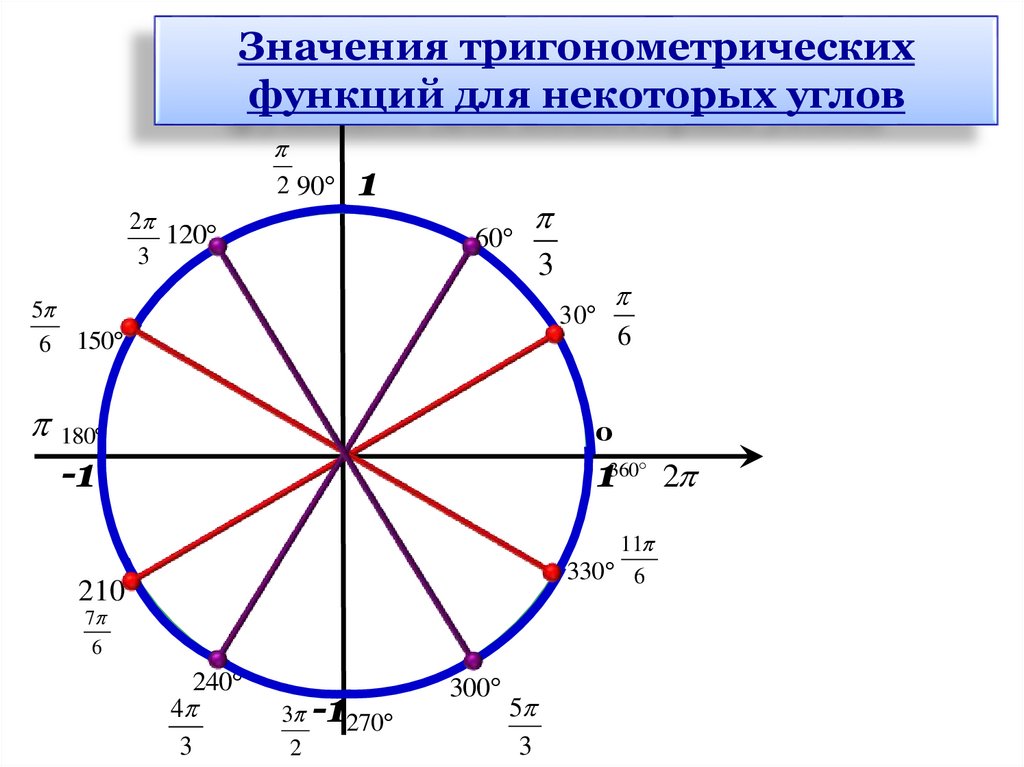
Значения тригонометрических
функций для некоторых углов
2 90
2
120
3
1
60
3
5
6 150
6
30
180
0
-1
1360 2
11
330 6
210
7
6
240
4
3
3
2
-1270
300
5
3

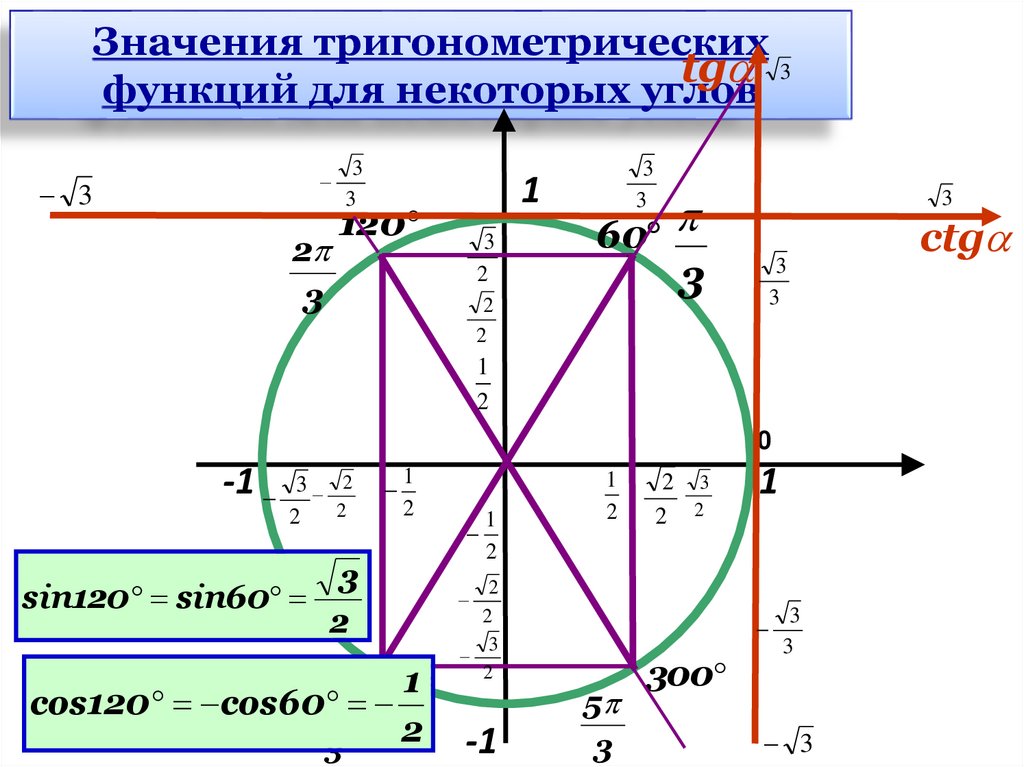
9.

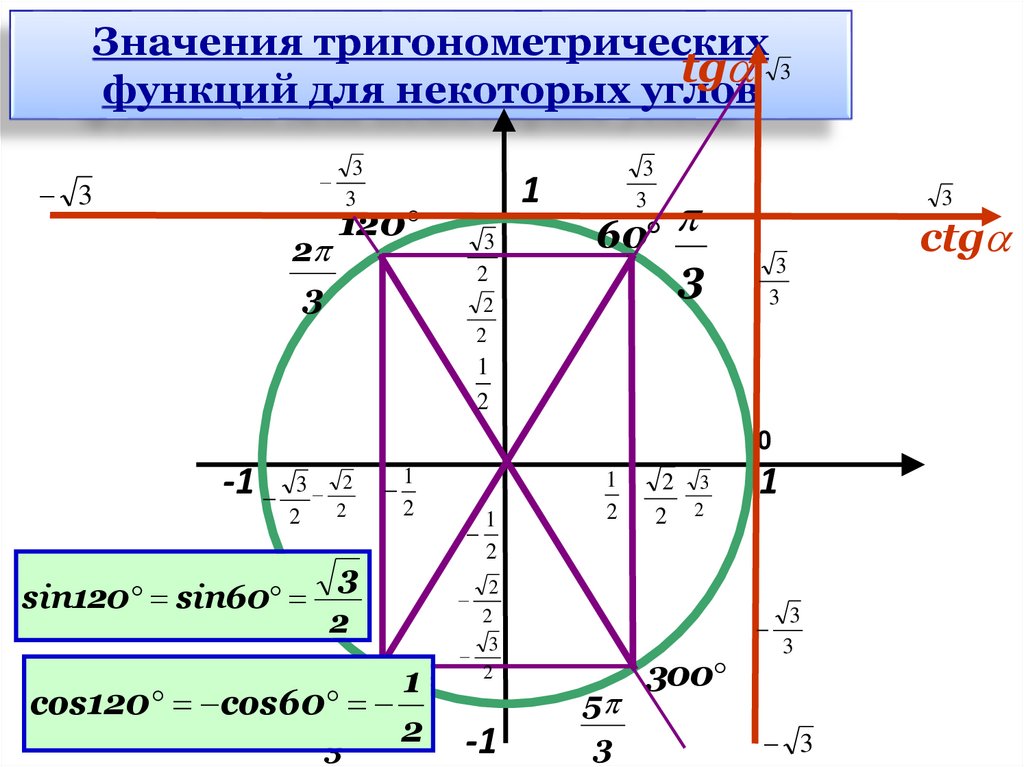
Значения тригонометрических
3
tg
функций для некоторых углов
3
3
3
2
3
1
120
3
2
3
3
60
3
3
2
2
3
3
1
2
0
-1 3 2
2
2
sin120 sin60
3
2
1
2
1
2
2
2
3
2
2 3
2 2
1
1
240
cos120 cos604
3
1
2
2
-1
5
3
300
3
3
3
ctg

10.

Значения тригонометрических
3
tg
функций для некоторых углов
3
3
3
2
3
1
120
3
2
3
3
60
3
3
2
2
3
3
1
2
0
-1 3 2
2
2
sin120 sin60
3
2
1
2
1
2
2
2
3
2
2 3
2 2
1
1
240
cos120 cos604
3
1
2
2
-1
5
3
300
3
3
3
ctg

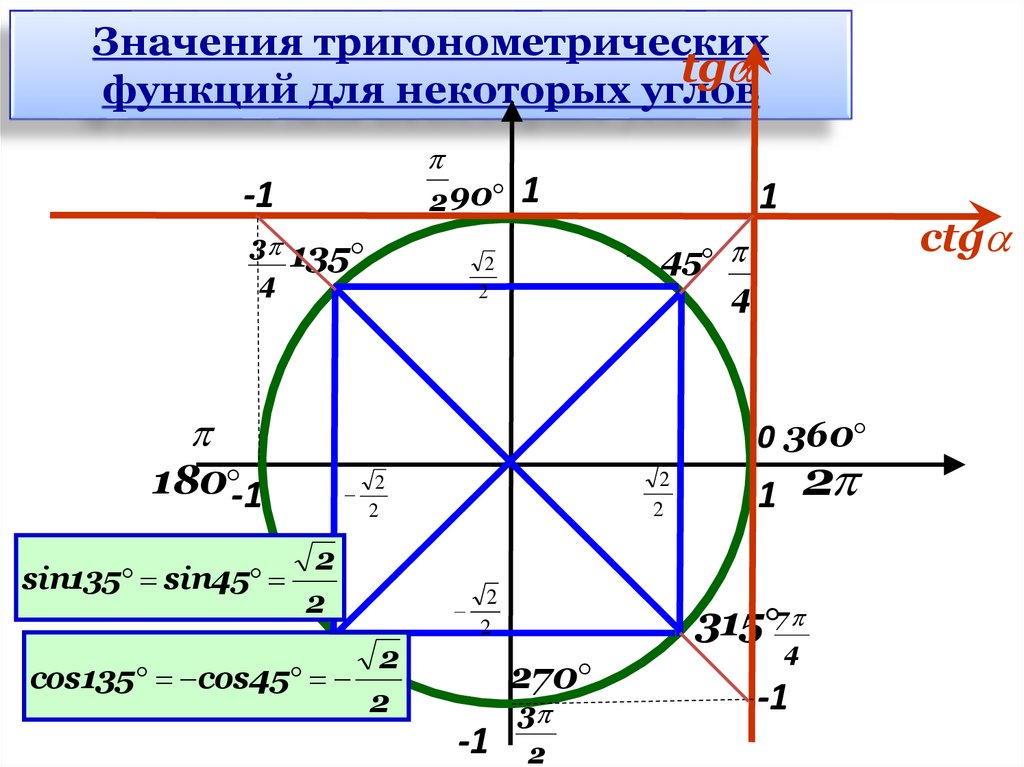
11.

Значения тригонометрических
tg
функций для некоторых углов
2 90 1
-1
3 135
4
180 -1
sin135 sin45
1
ctg
45
4
2
2
0 360
2
2
2
2
2
2
5 225 2
cos135 cos45
4
2
2
2
315 7
270
-1
1 2
3
2
4
-1

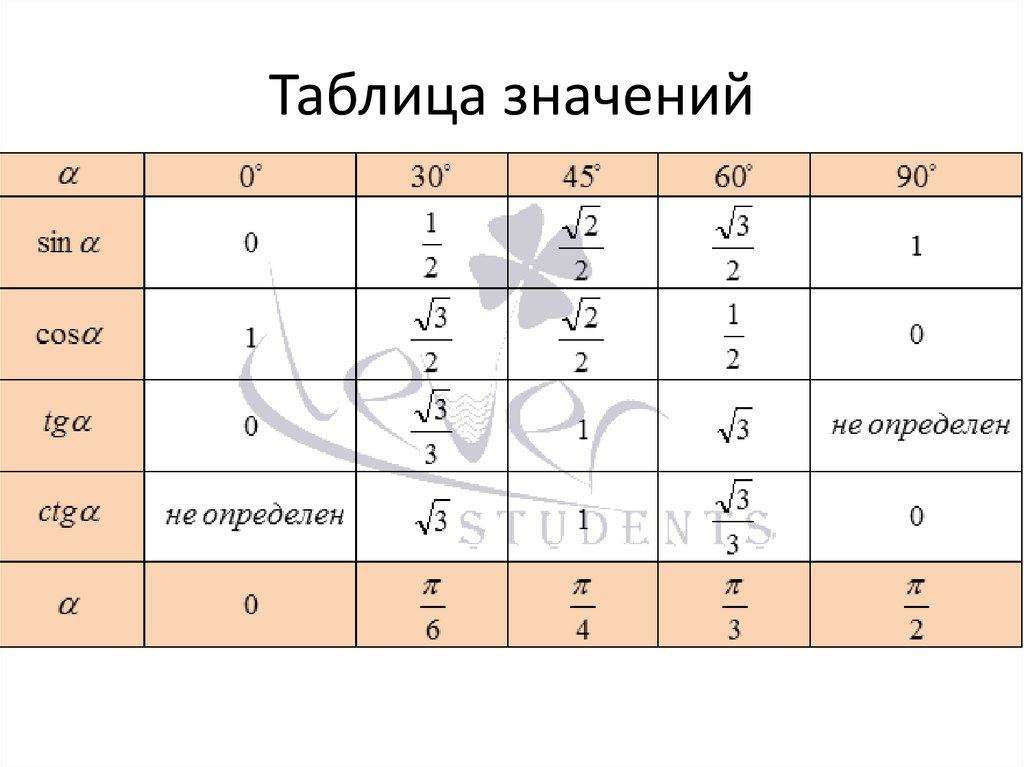
12. Таблица значений

13.

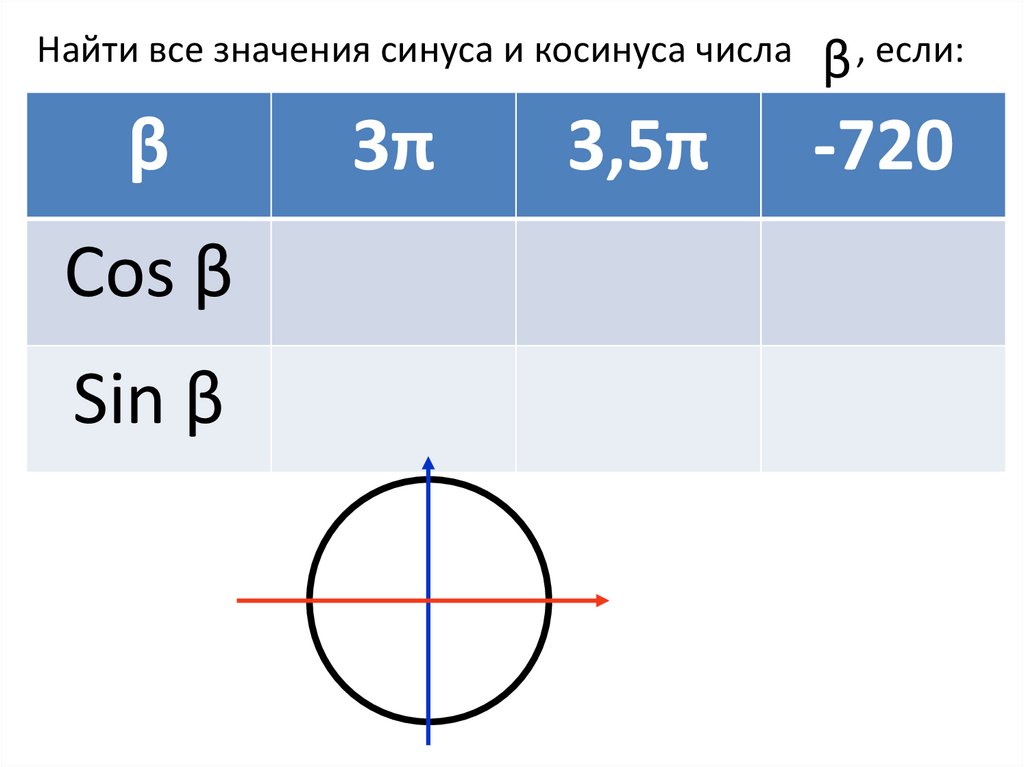
Найти все значения синуса и косинуса числа
β
Cos β
Sin β
3π
3,5π
β , если:
-720

14.

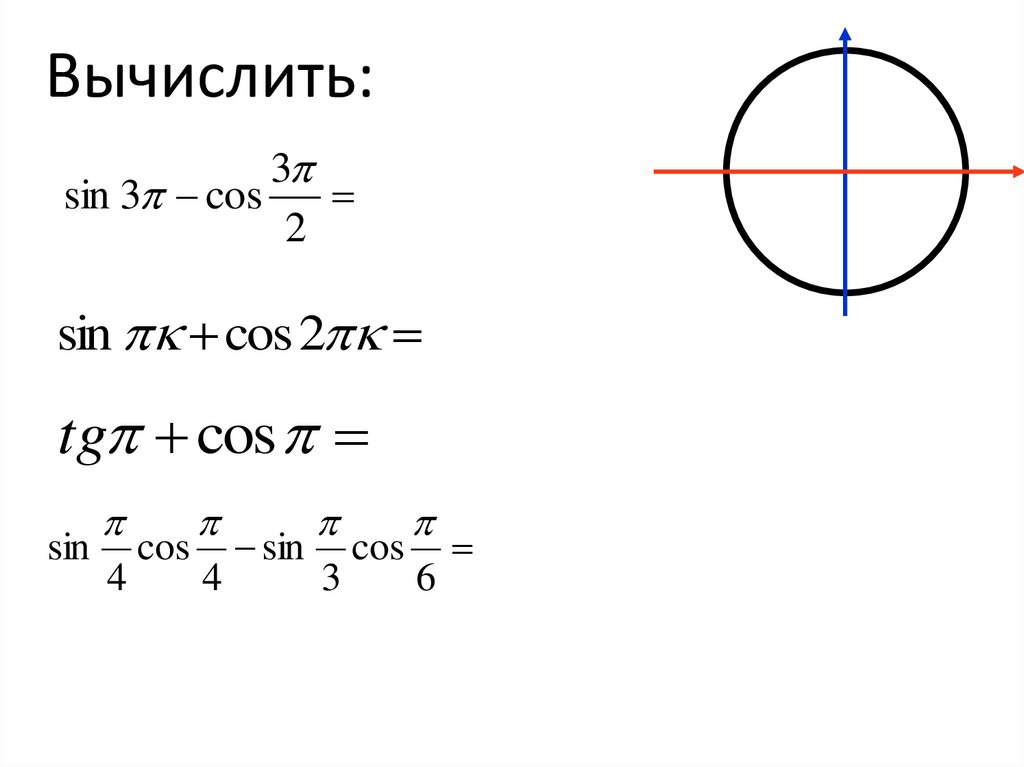
Вычислить:
3
sin 3 cos
2
sin cos 2
tg cos
sin
4
cos
4
sin
3
cos
6