10. ГЕОМЕТРИЧЕСКИЕ ТЕЛА

1. ГЕОМЕТРИЧЕСКИЕ ТЕЛА и точки на поверхностях тел

ГАПОУ СО «Уральский колледж
строительства, архитектуры и предпринимательства»
ГЕОМЕТРИЧЕСКИЕ ТЕЛА
и точки на поверхностях тел
Н.С. Оконишникова
Екатеринбург, 2009

2.

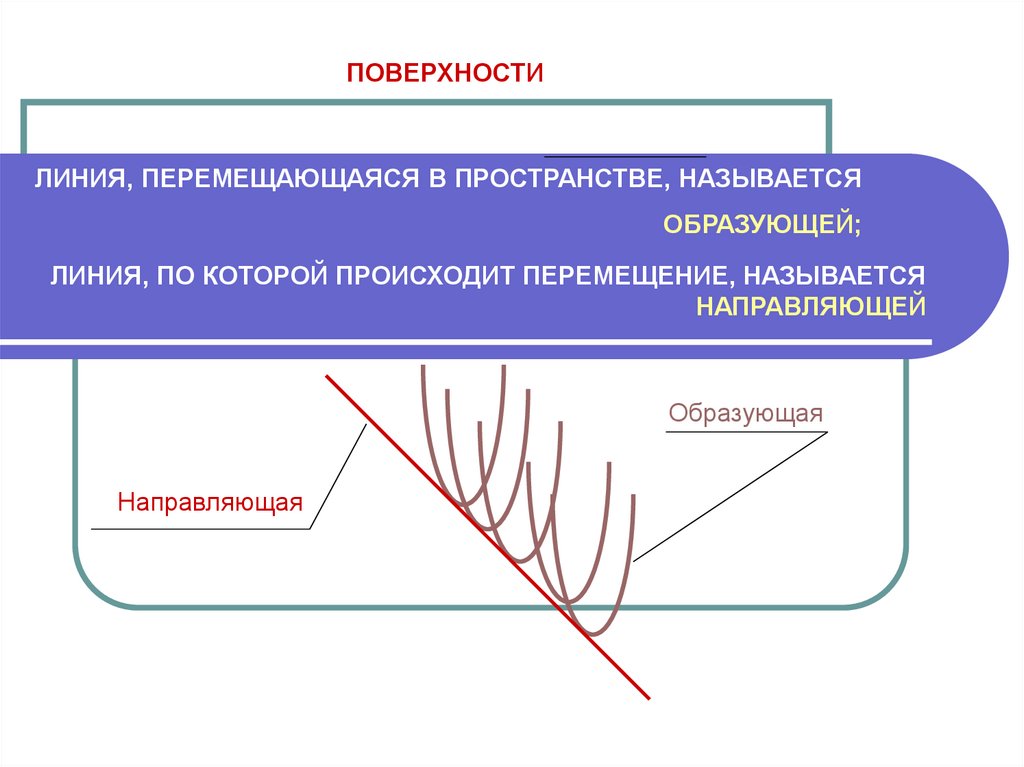
ПОВЕРХНОСТИ
ЛИНИЯ, ПЕРЕМЕЩАЮЩАЯСЯ В ПРОСТРАНСТВЕ, НАЗЫВАЕТСЯ
ОБРАЗУЮЩЕЙ;
ЛИНИЯ, ПО КОТОРОЙ ПРОИСХОДИТ ПЕРЕМЕЩЕНИЕ, НАЗЫВАЕТСЯ
НАПРАВЛЯЮЩЕЙ
Образующая
Направляющая

3. Образование поверхностей

3

4.

ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
Поверхность называется линейчатой, если она может быть
образована перемещением прямой линии.
Поверхность, которая не может быть образована движением
прямой линии, называется нелинейчатой. Например, конус
вращения - линейчатая поверхность, а сфера - нелинейчатая.
Через любую точку линейчатой поверхности можно провести, по
крайней мере, одну прямую, целиком принадлежащую
поверхности. Множество таких прямых представляет собой
непрерывный каркас линейчатой поверхности. Линейчатые
поверхности разделяются на два вида:
1) развертывающиеся поверхности;
2) неразвертывающиеся, или косые поверхности.
Примечание. Все нелинейчатые поверхности являются
неразвертывающимися.
4

5.

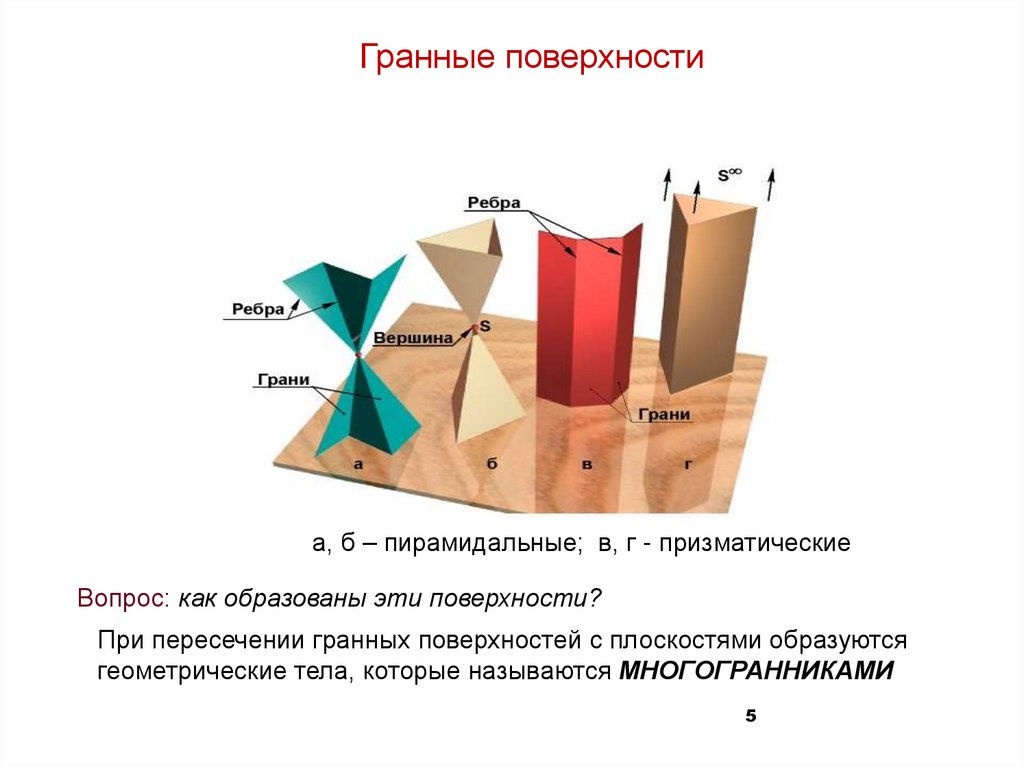
Гранные поверхности
Гранные поверхности
а, б – пирамидальные; в, г - призматические
Вопрос: как образованы эти поверхности?
При пересечении гранных поверхностей с плоскостями образуются
геометрические тела, которые называются МНОГОГРАННИКАМИ
5

6. Поверхности вращения

Поверхности вращения
ось вращения
При пересечении
поверхностей вращения с
плоскостями образуются
геометрические тела,
которые называются
телами вращения
образующая
6

7. Геометрические тела

геометрическим телом называется
часть пространства, ограниченная
со всех сторон поверхностями
7

8. Геометрические тела

Модели изделий
современного производства
состоят из сочетаний
геометрических тел
Вопрос: на поверхности
каких известных вам тел
можно разбить деталь,
изображённую на слайде?
1 – усечённый конус с отверстием;
2 – прямой круговой цилиндр;
3 – четырёхгранная призма;
4 – две четырёхгранные призмы с
отверстием;
5 – полуцилиндр с отверстием.
8

9. Многогранники

Многогранниками называются тела, все поверхности
которых – плоскости.
Плоскости эти называются гранями; различают плоскости основания и
боковых граней.
Пересекаются грани между собой по прямым линиям
– рёбрам (боковым и основания), точки схода рёбер
называются вершинами.
Если в основании многогранника лежит
правильный (равносторонний) многоугольник,
то многогранник называется правильным.
Задание. Найдите на чертеже призмы и назовите:
грани и рёбра оснований; боковые грани и рёбра.
Вопрос: Какое положение занимают рёбра призмы
по отношению к основаниям?
6
4
5
3
1
2
9

10.

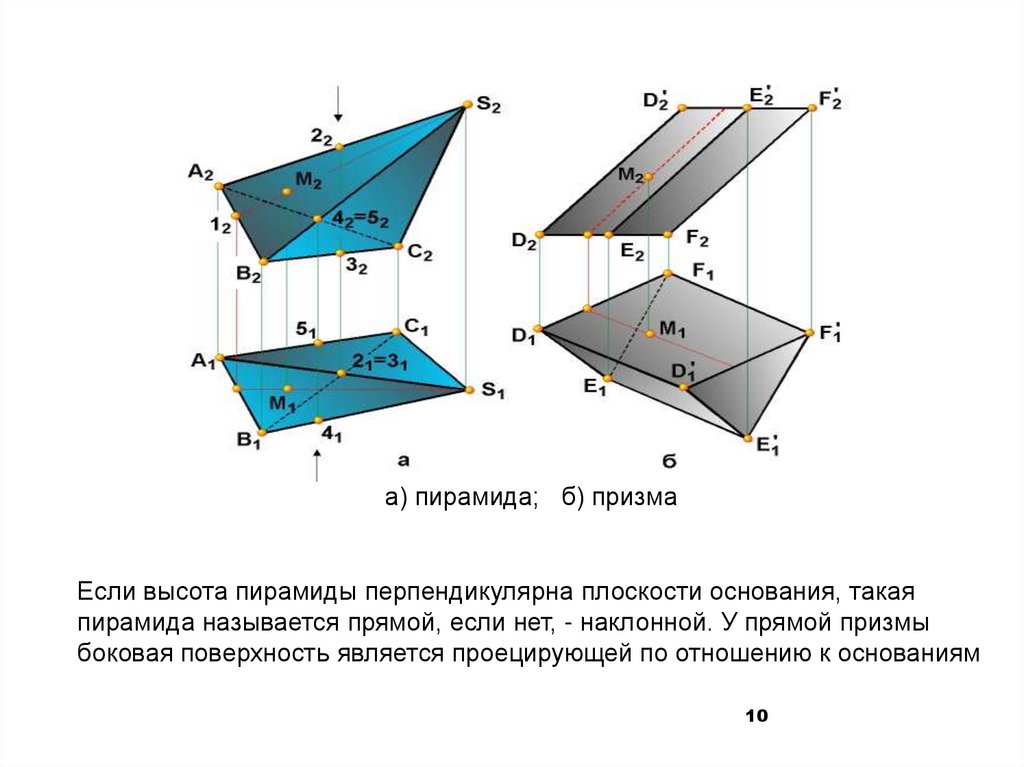
Многогранники
а) пирамида; б) призма
Если высота пирамиды перпендикулярна плоскости основания, такая
пирамида называется прямой, если нет, - наклонной. У прямой призмы
боковая поверхность является проецирующей по отношению к основаниям
10

11. Тела вращения

Прямой круговой цилиндр получается при пересечении круговой
цилиндрической поверхности (образующая перемещается по
замкнутой окружности, при этом оставаясь параллельной себе)
двумя перпендикулярными ей плоскостями.
Боковая поверхность цилиндра является
проецирующей по отношению к основаниям.
11

12. Тела вращения

Прямой круговой конус получается при пересечении круговой
конической поверхности (наклонная образующая перемещается
одним концом по замкнутой окружности, при этом второй конец
неподвижен и находится на оси вращения) одной или двумя
(если конус усечённый) перпендикулярными оси вращения
плоскостями.
При этом высота конуса, совпадающая с
осью вращения, проецируется в центр
основания.
Боковая поверхность конуса не является
проецирующей по отношению к плоскости
основания
12

13. Построение точек на поверхностях геометрических тел

Поверхности геометрических тел, моделирующих изделия, нередко
пересекаются друг с другом. При этом возникают линии
пересечения, состоящие из точек, принадлежащих обеим
пересекающимся поверхностям.
Построение этих линий невозможно без умения построить на
чертеже точку, принадлежащую поверхности тела.
13

14.

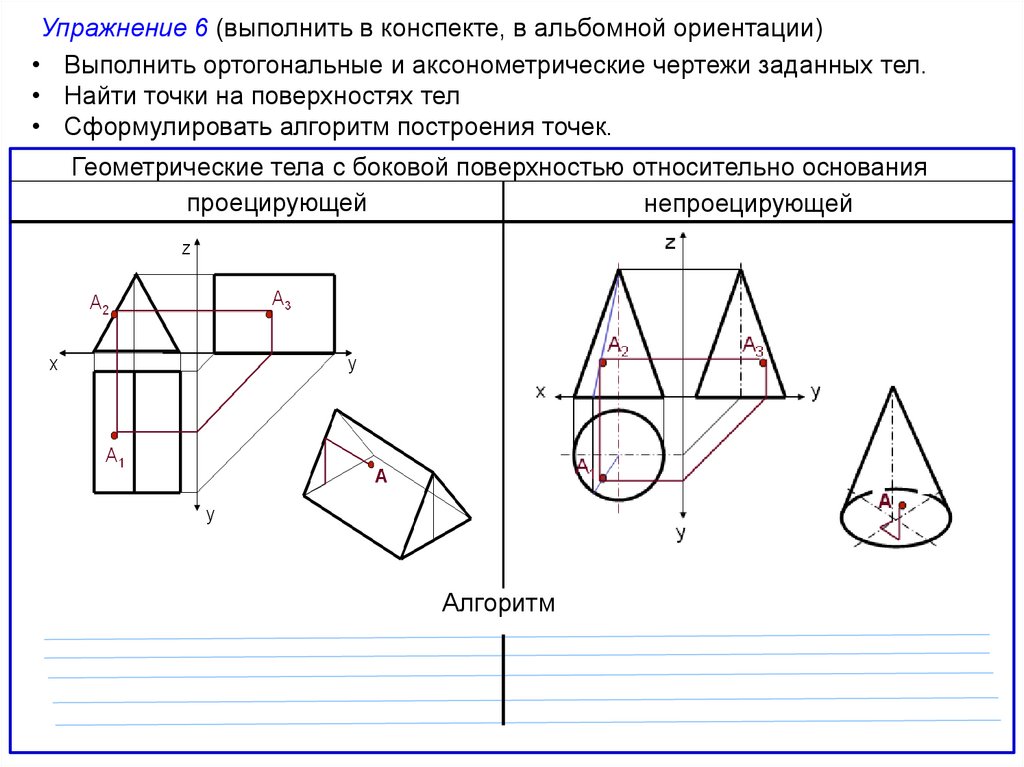
Упражнение 6 (выполнить
в конспекте, в альбомной
ориентации)
ГЕОМЕТРИЧЕСКИЕ
ТЕЛА
Построение точеки на
поверхностях
• Выполнить ортогональные
аксонометрические
и точки на поверхностях телчертежи заданных тел.
• геометрических
Найти точки на поверхностях
телтел
с проецирующей боковой поверхностью с непроецирующей боковой поверхностью
• Сформулировать алгоритм построения точек.
Геометрические тела с боковой поверхностью относительно основания
проецирующей
непроецирующей
Алгоритм

15. Построение эпюра тела с боковой поверхностью, перпендикулярной к плоскости основания (тело с проецирующей боковой поверхностью)

Построение
телаповерхностью,
с боковой поверхностью,
Тела сэпюра
боковой
проецирующей
перпендикулярной к плоскости основания (тело с
по отношению к плоскости основания
проецирующей боковой поверхностью)
z
x
y
y
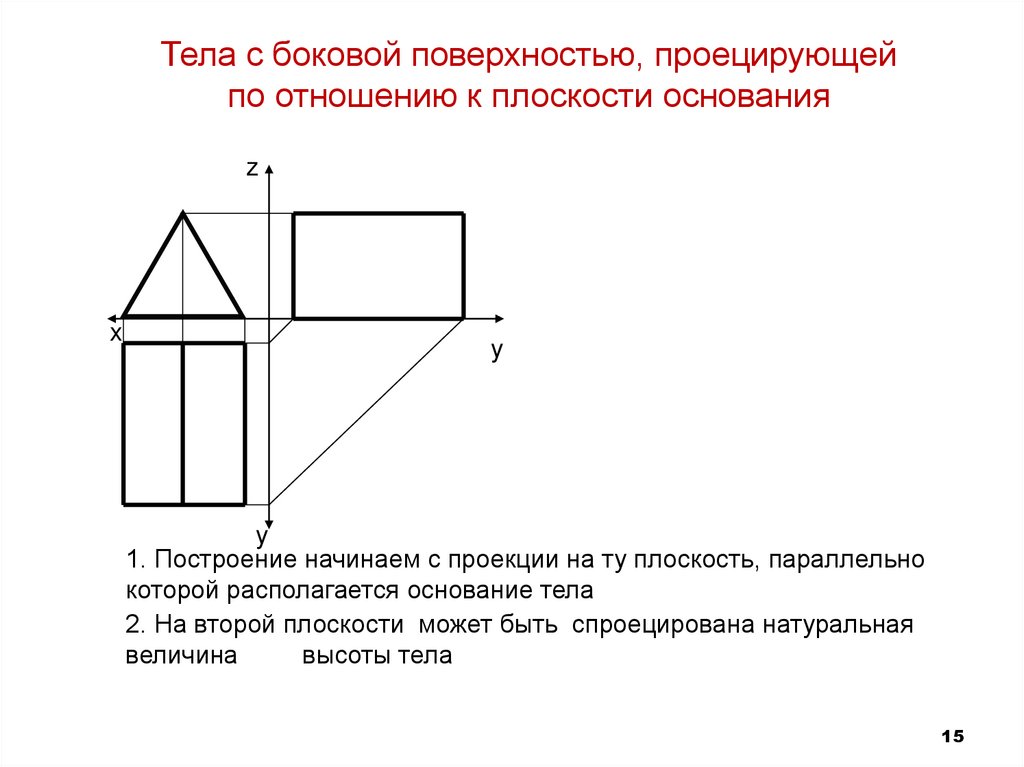
1. Построение начинаем с проекции на ту плоскость, параллельно
которой располагается основание тела
2. На второй плоскости может быть спроецирована натуральная
величина
высоты тела
15

16. Построение изометрической проекции тела с боковой поверхностью, перпендикулярной плоскости основания (тело с проецирующей

Построение
изометрической
проекции тела с проецирующей
боковой
Тела
с боковой поверхностью,
поверхностью, перпендикулярной плоскости основания (тело
по отношению к плоскости основания
с проецирующей боковой поверхностью)
z
x
y
y
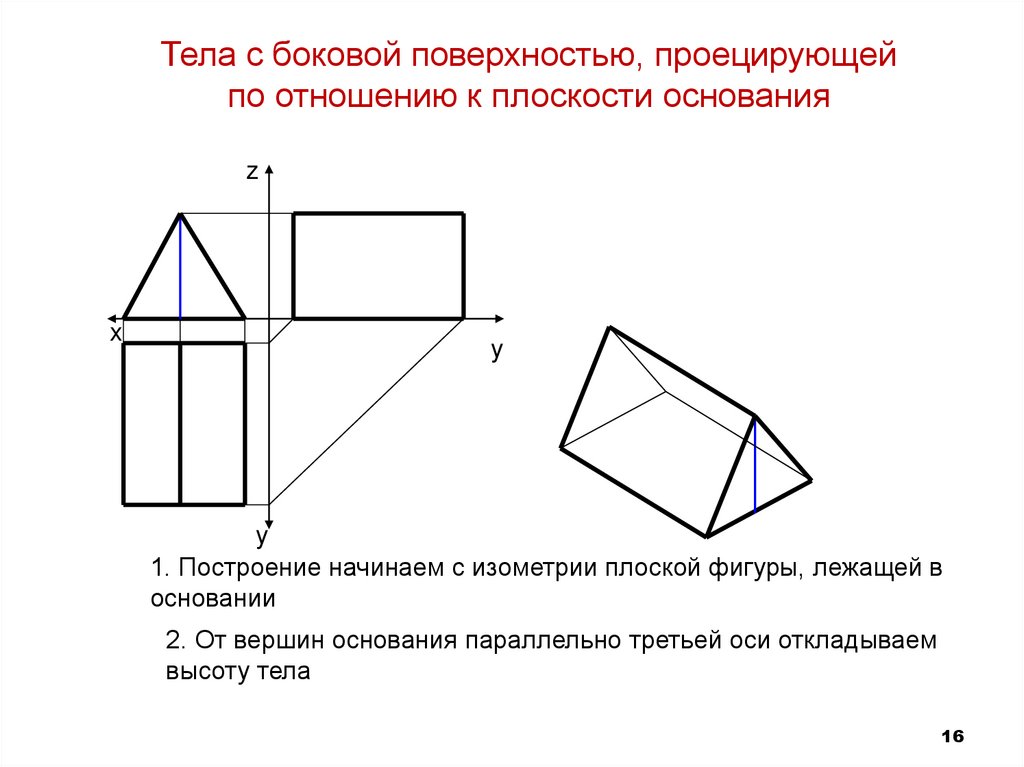
1. Построение начинаем с изометрии плоской фигуры, лежащей в
основании
2. От вершин основания параллельно третьей оси откладываем
высоту тела
16

17. Нахождение точки на поверхности тела с боковой поверхностью, перпендикулярной плоскости основания

Нахождение
точки
на поверхности
тела с боковой
Тела
с боковой
поверхностью,
проецирующей
поверхностью,по
перпендикулярной
плоскости основания
отношению к плоскости
основания
А2
А3
А1
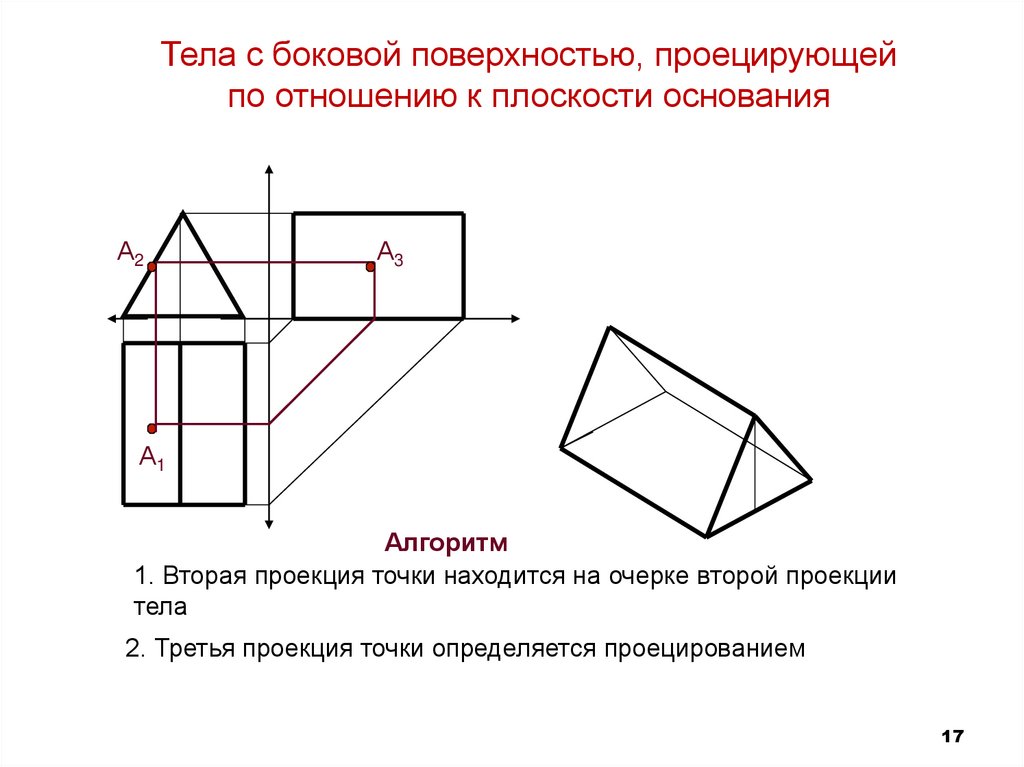
Алгоритм
1. Вторая проекция точки находится на очерке второй проекции
тела
2. Третья проекция точки определяется проецированием
17

18. Нахождение точки на поверхности тела с боковой поверхностью, перпендикулярной плоскости основания (тело с проецирующей боковой

Нахождение
точки
на поверхности
тела с боковой
Тела
с боковой
поверхностью,
проецирующей
поверхностью, перпендикулярной плоскости основания (тело
по отношению к плоскости основания
с проецирующей боковой поверхностью)
z
z
А3
А2
x
x
o y
y
А1
y
Алгоритм
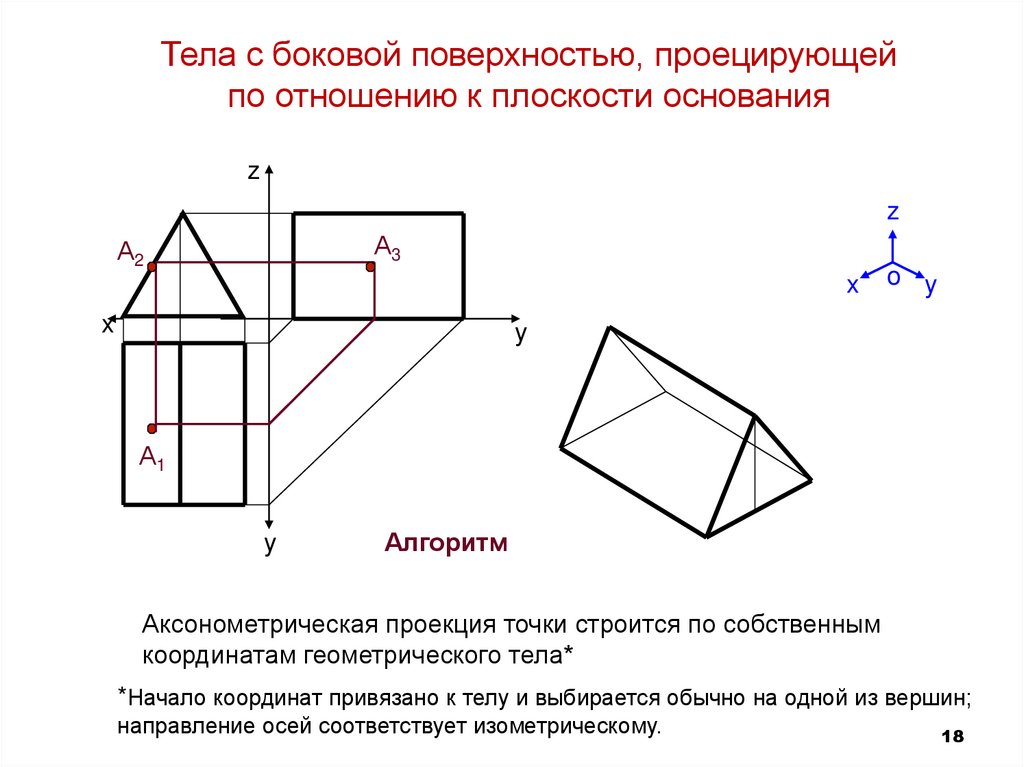
Аксонометрическая проекция точки строится по собственным
координатам геометрического тела*
*Начало координат привязано к телу и выбирается обычно на одной из вершин;
направление осей соответствует изометрическому.
18

19. Нахождение точки на поверхности тела с боковой поверхностью, перпендикулярной плоскости основания (тело с проецирующей боковой

Нахождение точки на поверхности тела с боковой поверхностью,
Тела с боковой поверхностью, проецирующей
перпендикулярной плоскости основания (тело с проецирующей
по отношению к плоскости основания
боковой поверхностью)
z
А3
А2
o2
x
y
o1
z
А
А1
x
o
y
y
Алгоритм
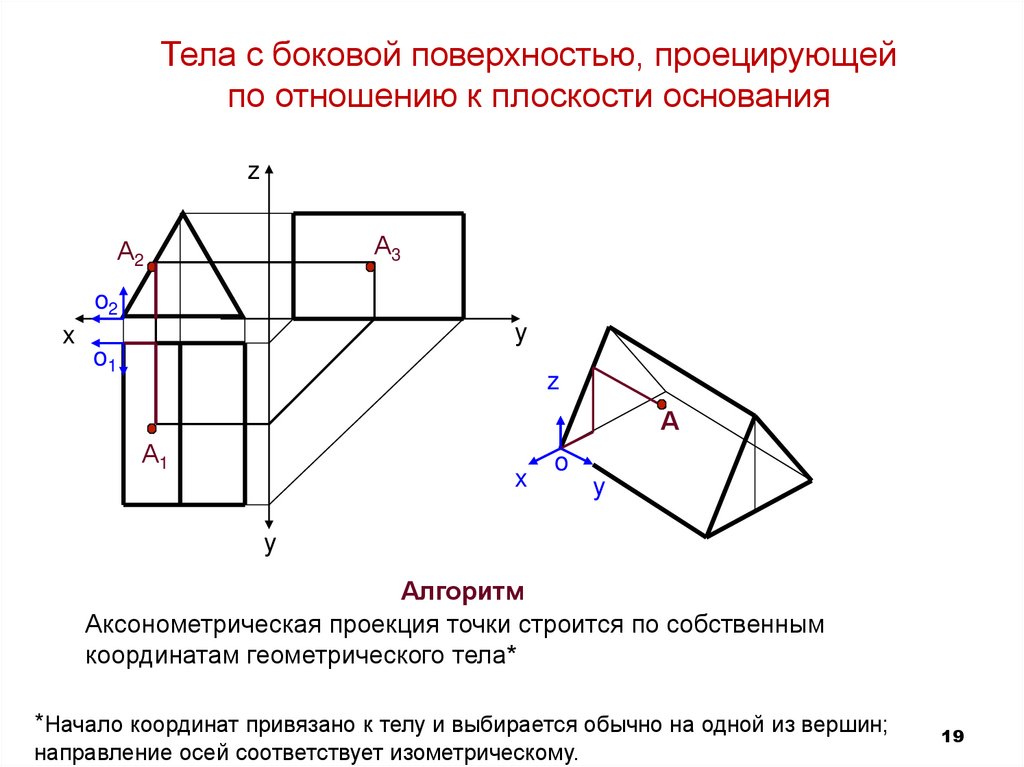
Аксонометрическая проекция точки строится по собственным
координатам геометрического тела*
*Начало координат привязано к телу и выбирается обычно на одной из вершин;
направление осей соответствует изометрическому.
19

20. Нахождение точки на поверхности тела, боковая поверхность которого расположена наклонно к плоскости основания

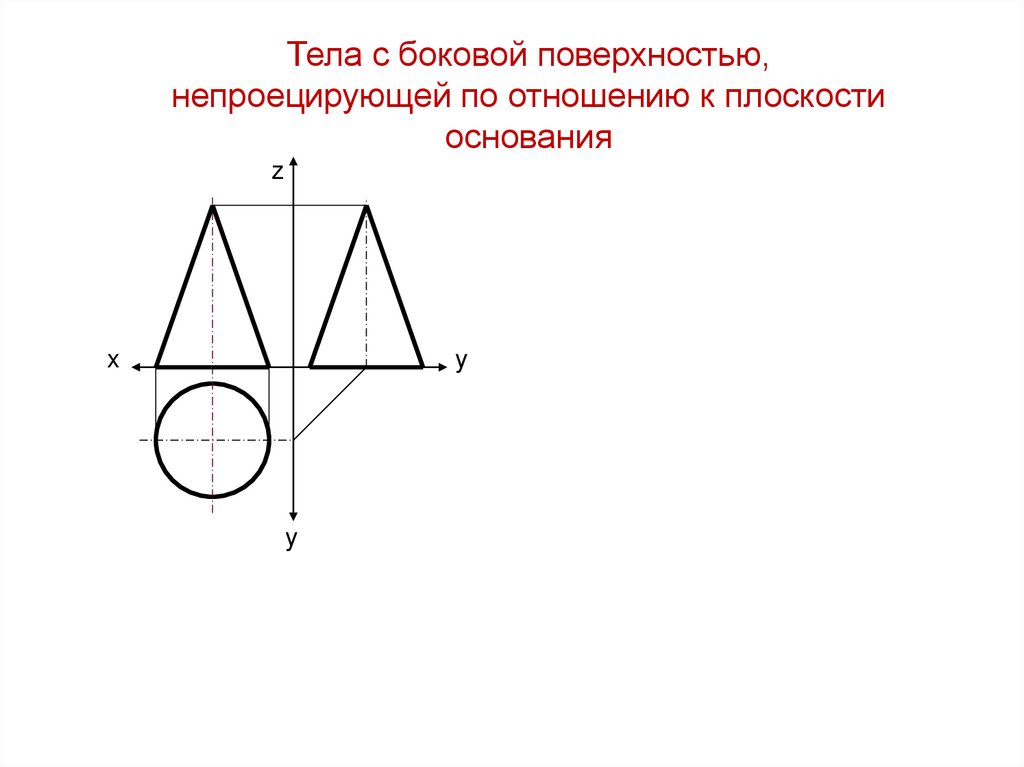
Нахождение точки на поверхности тела, боковая
Тела с боковой поверхностью,
поверхность которого расположена наклонно к
непроецирующей по отношению к плоскости
плоскости основания
основания
z
x
y
y

21. Нахождение точки на поверхности тела, боковая поверхность которого расположена наклонно к плоскости основания (тело с

Нахождение точки наТела
поверхности
тела,поверхностью,
боковая поверхность
с боковой
которого расположена
наклонно к по
плоскости
основания
(тело с
непроецирующей
отношению
к плоскости
нпроецирующей боковой поверхностью)
основания
z
x
y
y

22. Нахождение точки на поверхности тела, боковая поверхность которого расположена наклонно к плоскости основания (тело с

Нахождение точки на поверхности тела, боковая поверхность
Тела с боковой поверхностью,
которого расположена наклонно к плоскости основания (тело с
непроецирующей
по отношению к плоскости
непроеирующей
боковой поверхностью)
основания
z
посредник
А2
x
А3
y
А1
y
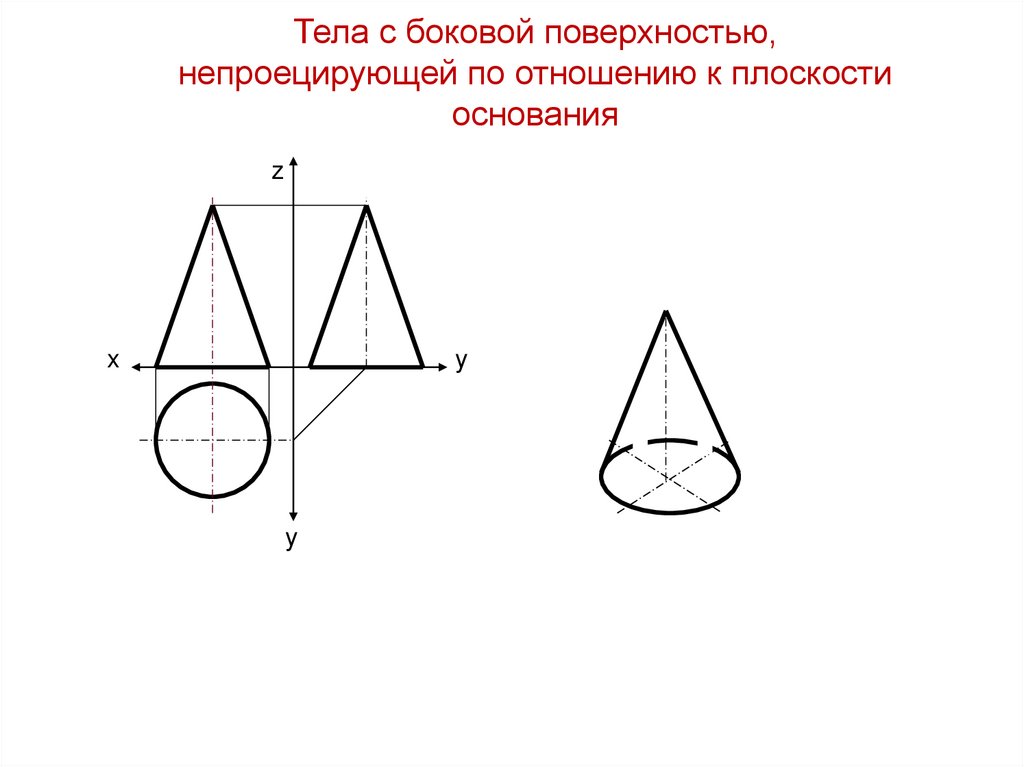
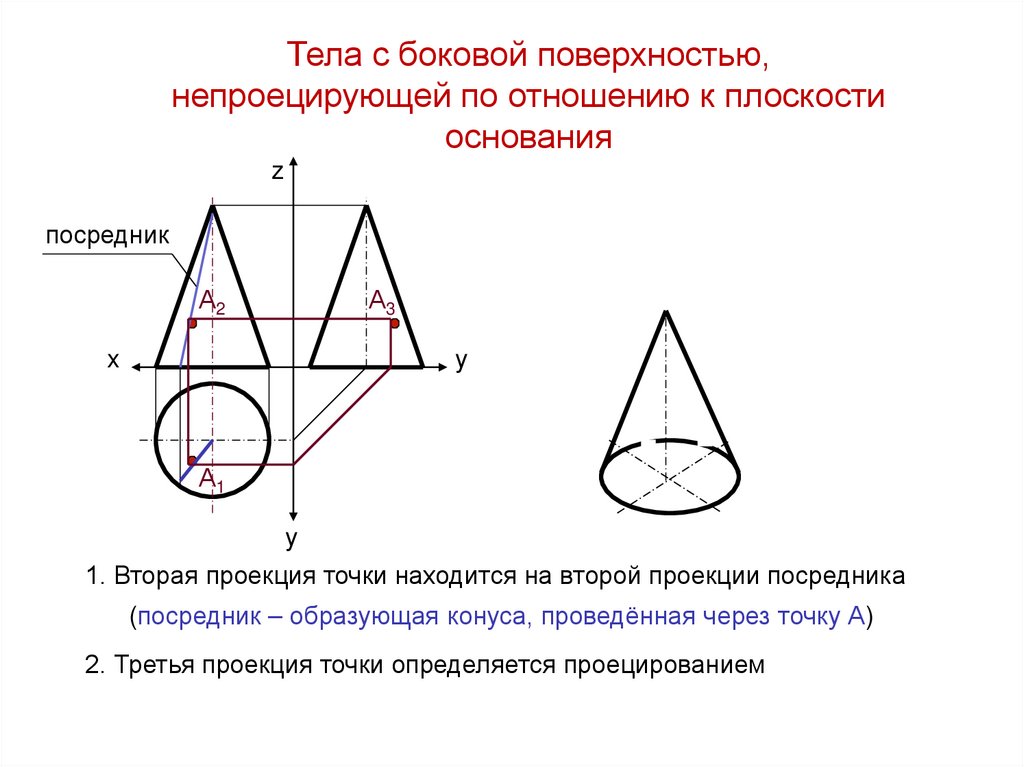
1. Вторая проекция точки находится на второй проекции посредника
(посредник – образующая конуса, проведённая через точку А)
2. Третья проекция точки определяется проецированием

23. Нахождение точки на поверхности тела, боковая поверхность которого расположена наклонно к плоскости основания (тело с

Нахождение точки на поверхности тела, боковая поверхность
Тела с боковой поверхностью,
которого расположена наклонно к плоскости основания (тело с
непроецирующей
по отношению к плоскости
непроецирующей
боковой поверхностью)
основания
z
А2
А3
x
y
z
А1
y
x
y
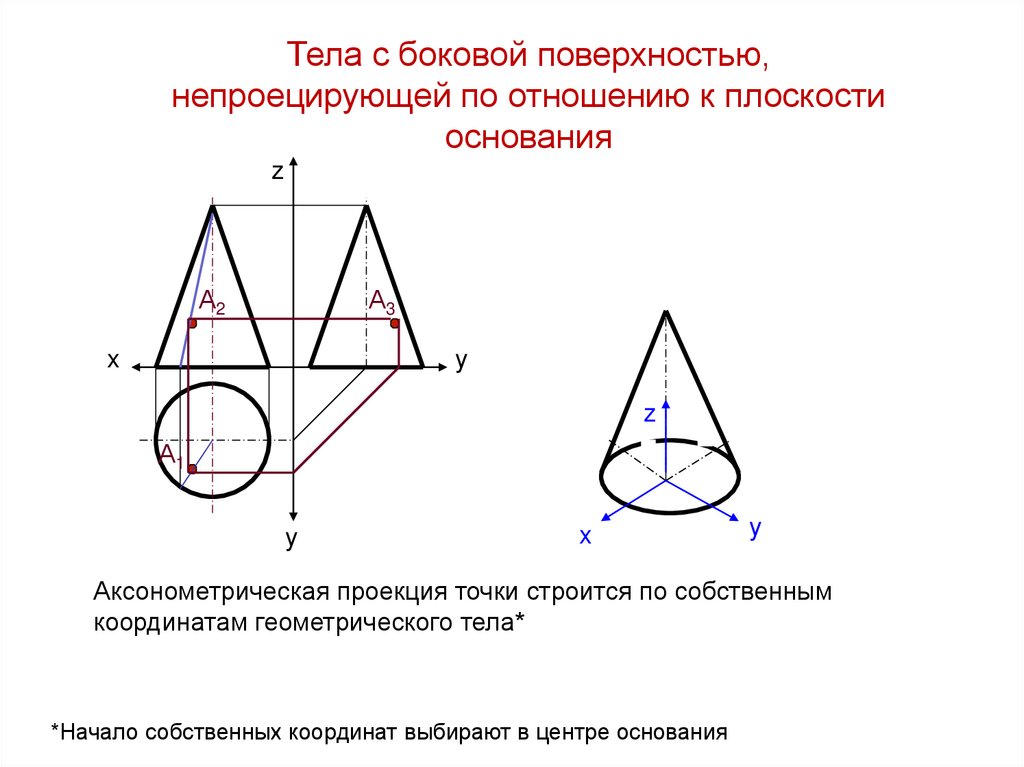
Аксонометрическая проекция точки строится по собственным
координатам геометрического тела*
*Начало собственных координат выбирают в центре основания

24.

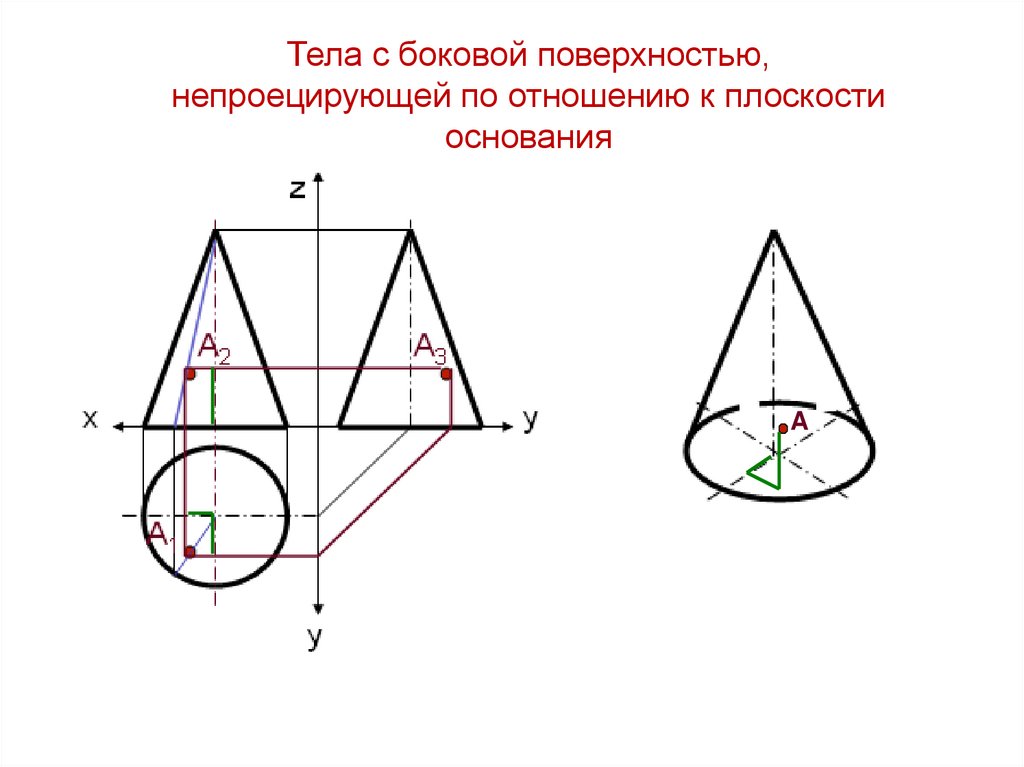
Тела с боковой поверхностью,
непроецирующей по отношению к плоскости
основания
A

25.

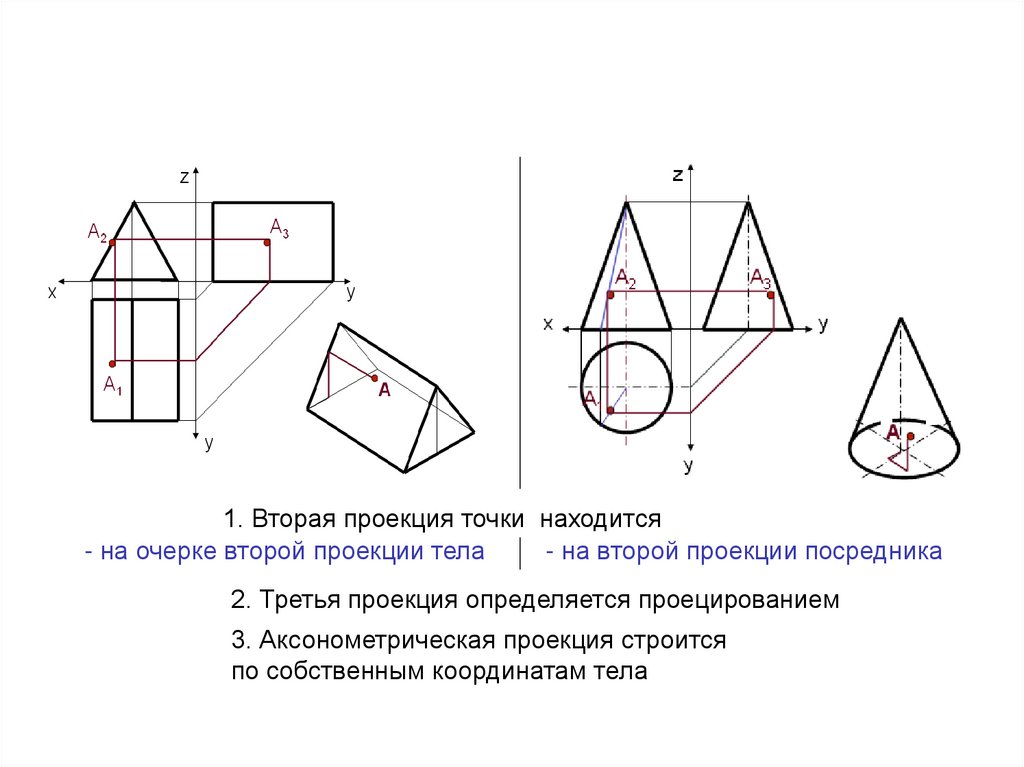
Алгоритм
1. Вторая проекция точки находится
- на очерке второй проекции тела
- на второй проекции посредника
2. Третья проекция определяется проецированием
3. Аксонометрическая проекция строится
по собственным координатам тела

26.

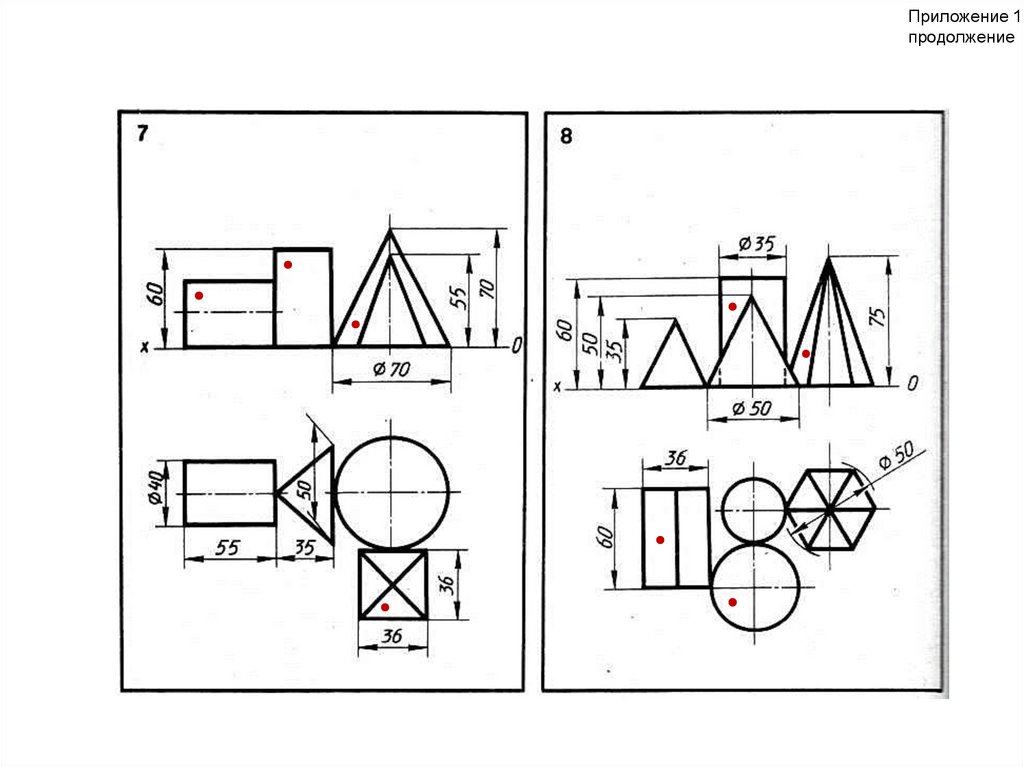
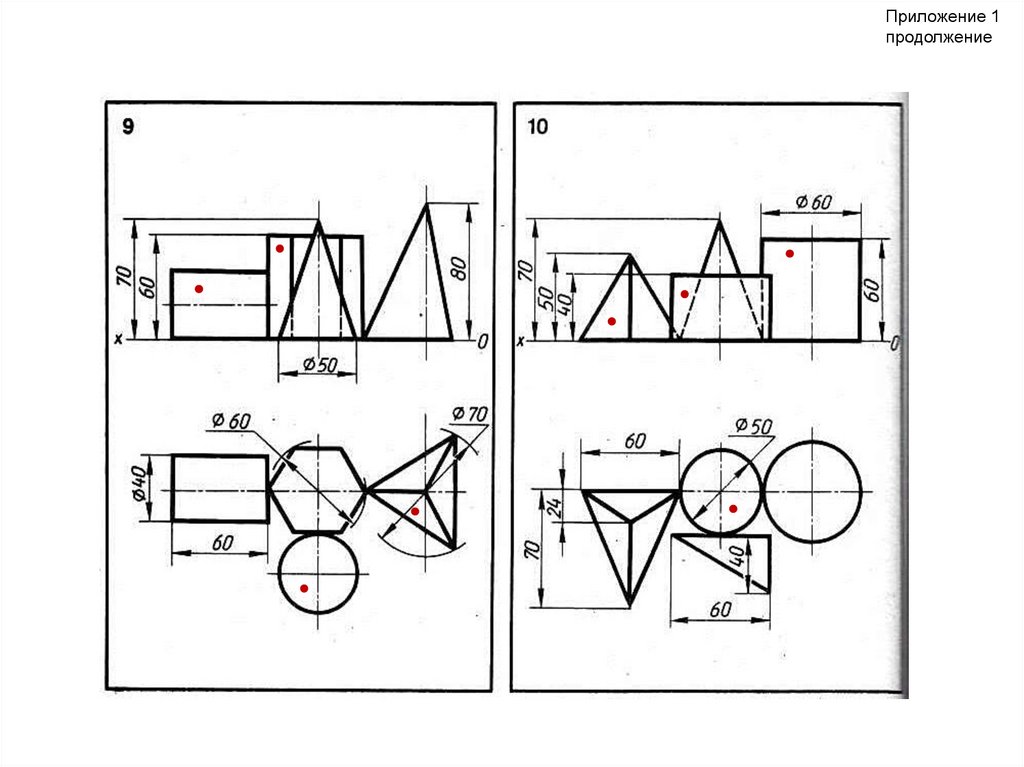
Графическая работа №3 – Проекции группы тел*
(формат А3)
1. Построить три проекции группы из четырёх геометрических тел (призмы,
пирамиды, цилиндра и конуса), сохранив их взаимное расположение
2. Выполнить изометрическую проекцию группы (при недостатке места можно
использовать второй лист формата А3)
3. На боковых поверхностях каждого тела самостоятельно задать и построить на
ортогональном и аксонометрическом чертежах по одной точке. Точки обозначить
латинскими буквами (A, B, C, D), обозначения их ортогональных проекций
дополнить индексом, присвоенным плоскостям проекций (например: А1, A2, A3).
*Варианты задания см. Приложение 1

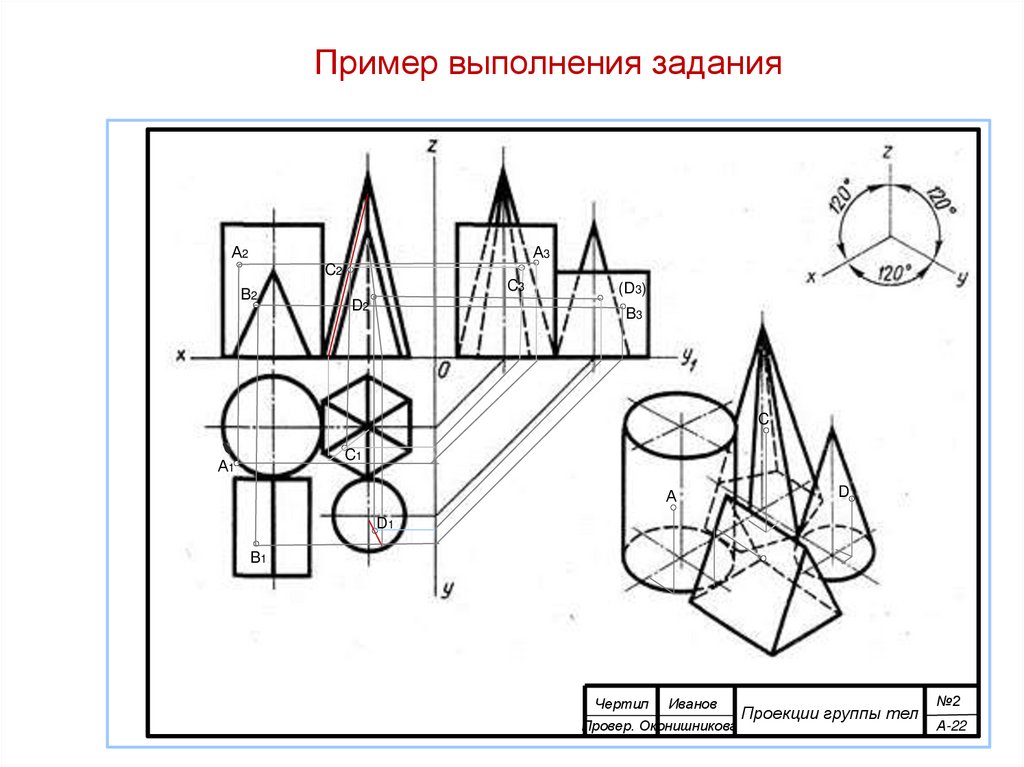
27. Пример выполнения графической работы «Проекции группы тел»

Пример выполнения
графической
Пример выполнения
задания
работы «Проекции группы тел»
А2
А3
C2
B2
C3
D2
(D3)
B3
C
C1
А1
А
D
D1
B1
Чертил
Иванов
Провер. Оконишникова
Проекции группы тел
№2
А-22

28.

Методические указания
1. Перед началом работы изучить теоретический материал.
2. Ознакомиться с заданием на практическую работу. Вариант задания
выбирается по последним двум цифрам студенческого билета (например,
вариант 1 выбирают студенты, у которых две последние цифры 01, 11, 21,
31 и т.д.).
3. Продумать компоновку чертежа, ориентируясь на образец выполнения
задания
4. Вычертить две проекции в соответствии с заданием по заданным
размерам (размеры не проставлять).
5. Выполнить необходимые для решения задачи построения на
ортогональном чертеже, сохраняя все линии проекционной связи.
Невидимые контуры показать штриховой линией.
6. Построить изометрическую проекцию. Невидимые контуры показать
сплошной тонкой линией.
7. Заполнить основную надпись.

29.

Библиография
Библиография
1. Лукинских, С.В. и др. Инженерная графика: Портфель преподавателя
[Электронный ресурс]: Учеб. пособие для студ. вузов. – Екатеринбург:
УГТУ – УПИ, 2009
2. Швайгер, А.М. Начертательная геометрия [Электронный ресурс]:
Учеб. для студ. тех. спец. вузов и тех-мов. – Челябинск: ЮрГУ, 2002

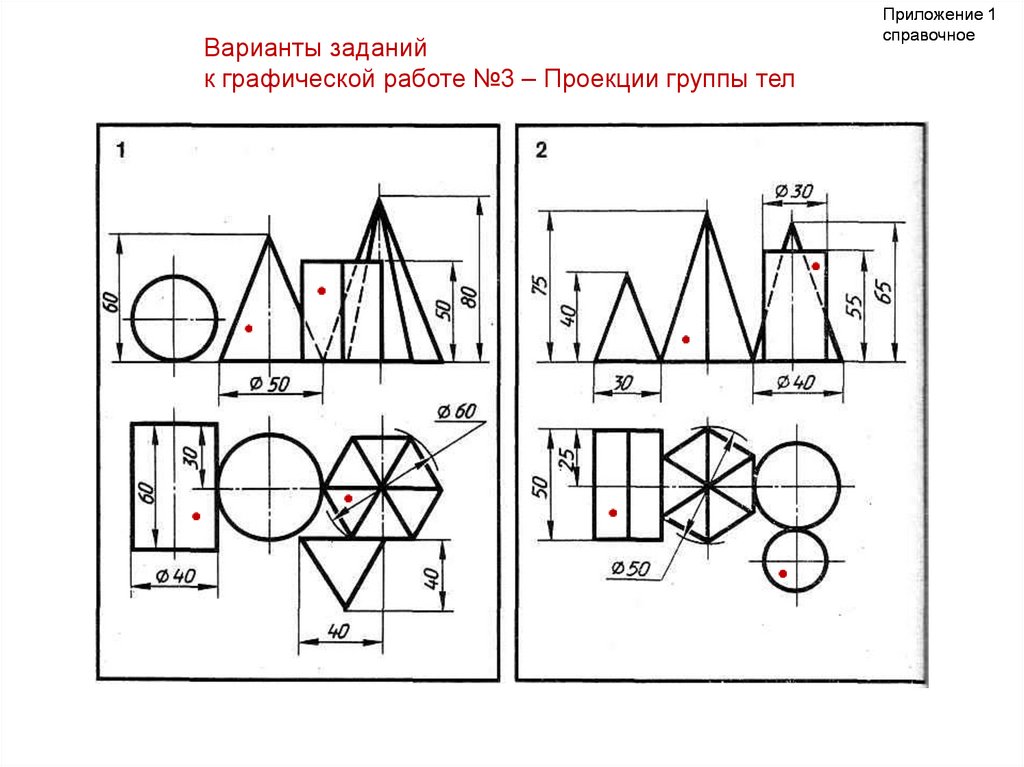
30.

Варианты заданий
к графической работе №3 – Проекции группы тел
Приложение 1
справочное

31.

Приложение 1
справочное

32.

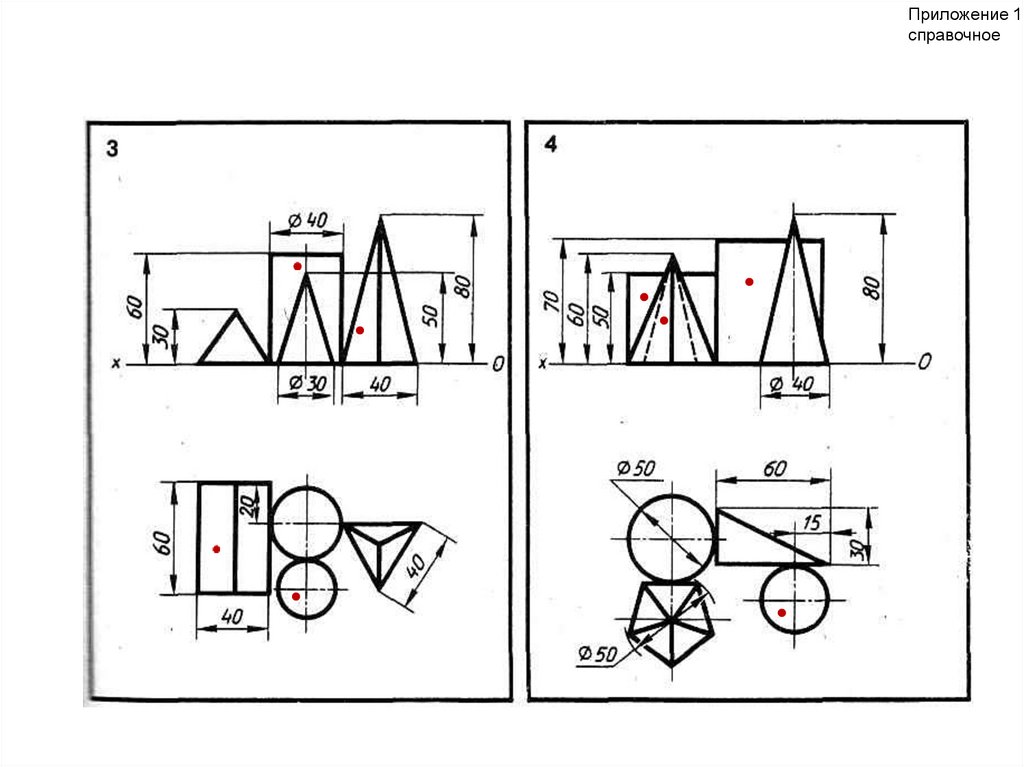
Приложение 1
продолжение

33.

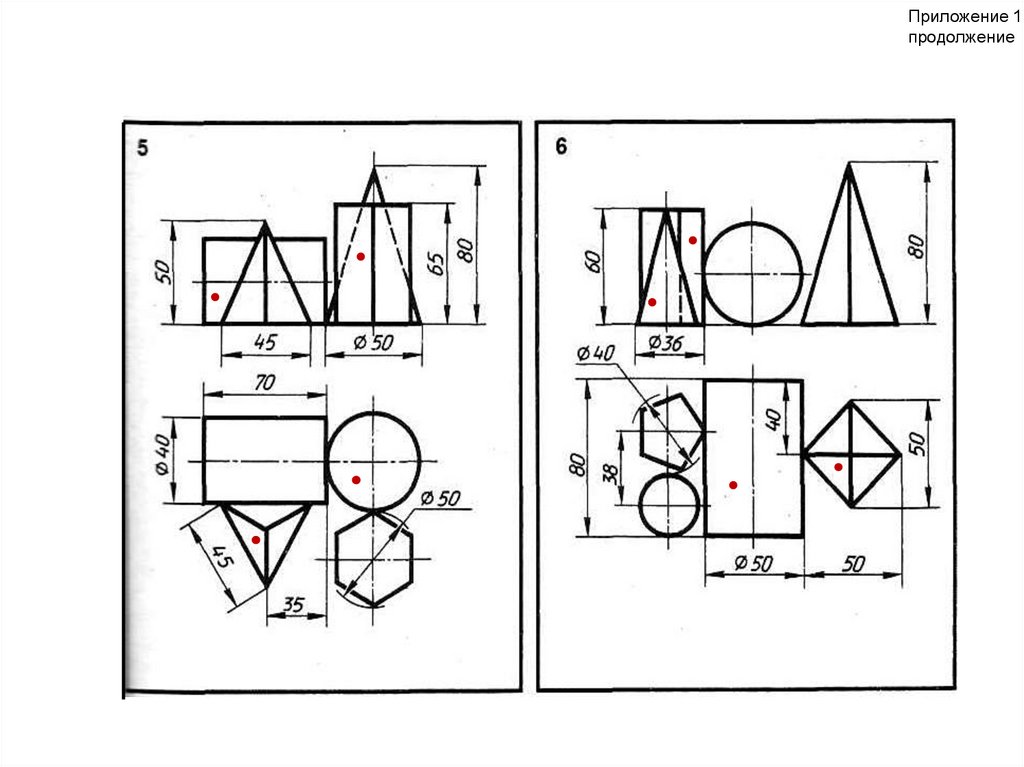
Приложение 1
продолжение

34.

Приложение 1
продолжение