Similar presentations:
Рабочая тетрадь
1.
МГТУ им.Н.Э. Баумана
Рабочая тетрадь
для практических занятий по начертательной геометрии
Задачи для самостоятельной работы студентов
Авторы: доценты, к.т.н. Сенченкова Л.С., к.т.н. Палий Н.В., ст. пр. Белобородова Т.Л.
под редакцией доцента, к.т.н. Боровикова И.Ф.
2.
СОДЕРЖАНИЕПРОЕКЦИИ ТОЧКИ ▼
ЗАДАНИЕ ПРЯМОЙ ЛИНИИ НА ЧЕРТЕЖЕ ▼
ЗАДАНИЕ ПЛОСКОСТИ НА ЧЕРТЕЖЕ. ТОЧКА И ПРЯМАЯ В ПЛОСКОСТИ ▼
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ ▼
ПРОЕКЦИИ МНОГОГРАННИКОВ ▼
СПОСОБЫ ПРЕОБРАЗОВАНИЯ. МЕТРИЧЕСКИЕ ЗАДАЧИ ▼
Способ замены плоскостей проекций ▼
Способ плоскопараллельного перемещения ▼
Способ вращения вокруг проецирующей прямой ▼
Композиция преобразований ▼
7. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТЕЙ ▼
Поверхности вращения ▼
Винтовая поверхность ▼
1.
2.
3.
4.
5.
6.
Для в перехода к нужному разделу требуется нажать знак ▼
3.
СОДЕРЖАНИЕ8.
ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР ▼
Пересечение многогранников проецирующей плоскостью ▼
Пересечение тел вращения проецирующей плоскостью ▼
Пересечение прямой и плоскости, двух плоскостей ▼
Пересечение прямой линии и поверхности ▼
Пересечение поверхностей, одна из которых проецирующая ▼
Пересечение поверхностей с использованием вспомогательных проецирующих плоскостей
▼
Пересечение поверхностей. Частные случаи ▼
9. ПЛОСКОСТЬ, КАСАТЕЛЬНАЯ К ПОВЕРХНОСТИ, НОРМАЛЬ ПОВЕРХНОСТИ ▼
10.
РАЗВЕРТКА ПОВЕРХНОСТЕЙ ▼
11. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ ▼
Для в перехода к нужному разделу требуется нажать знак ▼
4.
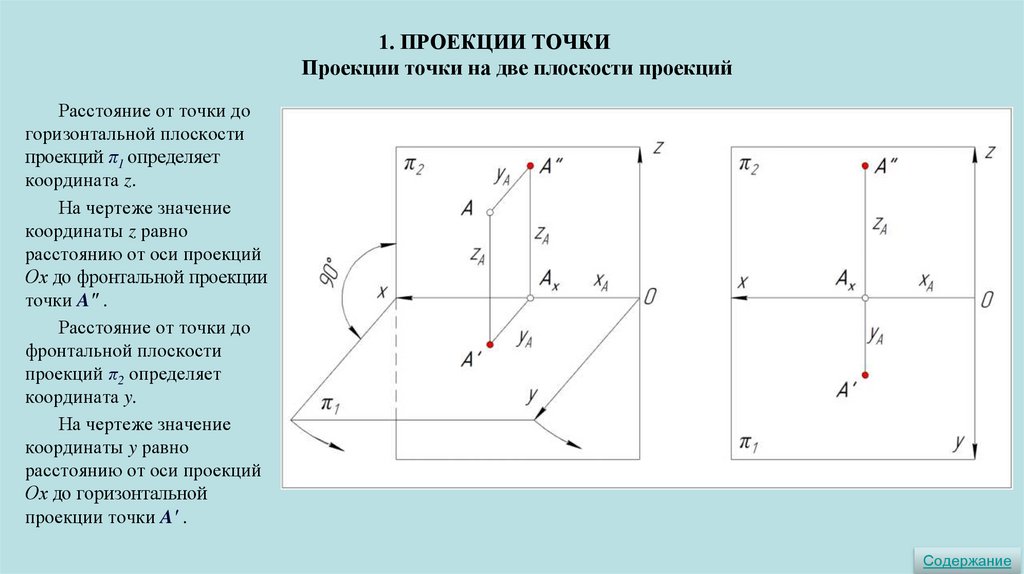
1. ПРОЕКЦИИ ТОЧКИПроекции точки на две плоскости проекций
Расстояние от точки до
горизонтальной плоскости
проекций π1 определяет
координата z.
На чертеже значение
координаты z равно
расстоянию от оси проекций
Оx до фронтальной проекции
точки Aʺ .
Расстояние от точки до
фронтальной плоскости
проекций π2 определяет
координата y.
На чертеже значение
координаты y равно
расстоянию от оси проекций
Оx до горизонтальной
проекции точки A′ .
Содержание
5.
Проекции точки на три плоскости проекцийРасстояние от точки до
профильной плоскости
проекций π3 определяет
координата х.
На чертеже значение
координаты х равно расстоянию
от оси проекций Оz до
фронтальной проекции точки
или от оси проекций Оy до
горизонтальной проекции
точки.
Горизонтальная проекция A′
точки A определяется
координатами х, y.
Фронтальная проекция Aʺ
точки A определяется
координатами х, z.
Профильная проекция A′′′
точки A определяется
координатами y, z.
Содержание
6.
1.8*. Построить проекции точки A, лежащей в плоскости проекций π2 иудаленной от плоскости π1 на расстояние 30 мм, от π3 – на 40 мм.
Горизонтальная проекция A′ точки A
определяется координатами x, y;
Фронтальная проекция Aʺ точки A
определяется координатами x, z;
Профильная проекция A′′′ точки A
определяется координатами у, z.
Расстояние от точки до профильной
плоскости проекций π3 определяет
координата х (xA = 40).
Расстояние от точки до горизонтальной
плоскости проекций π1 определяет
координата z (zA = 30).
Если точка А ∈ π2 , то yA = 0
Для решения задачи воспользуемся
последовательно значениями координат:
xA = 40; yA = 0; zA = 30.
Содержание
7.
1.9*. Построить проекции точки A, лежащей на оси проекций Oх иудаленной от плоскости проекций π3 на расстояние 40 мм.
Расстояние от точки до профильной
плоскости проекций π3 определяет
координата х (xA = 40);
Если точка А ∈ Ох, то yA = 0, zA = 0.
Для решения задачи воспользуемся
последовательно значениями
координат:
A′ (x, y); Aʺ (x, z); A′′′ (у, z),
а именно:
A′ (40, 0); Aʺ (40, 0); A′′′ (0, 0).
Содержание
8.
1.10*. Построить проекции точки В, которая относительно точки Aрасположена на 15 мм дальше от плоскости проекций π1 , на 20 мм
ближе к π2 и на 10 мм дальше от π3 .
Построение с использованием разности
координат можно начинать в следующем
порядке:
– определяем горизонтальную проекцию
точки В′ (xВ ; yВ ):
xВ > xA на 10 мм; xВ = xA + 10 мм;
yВ < yA на 20 мм; yВ = yA – 20 мм;
– определяем фронтальную проекцию
точки Вʺ(xВ ; zВ ):
zВ > zA на 15 мм; zВ = zA + 15 мм.
Профильная
проекция
точки
В′′′
определяется координатами yВ ; zВ .
Содержание
9.
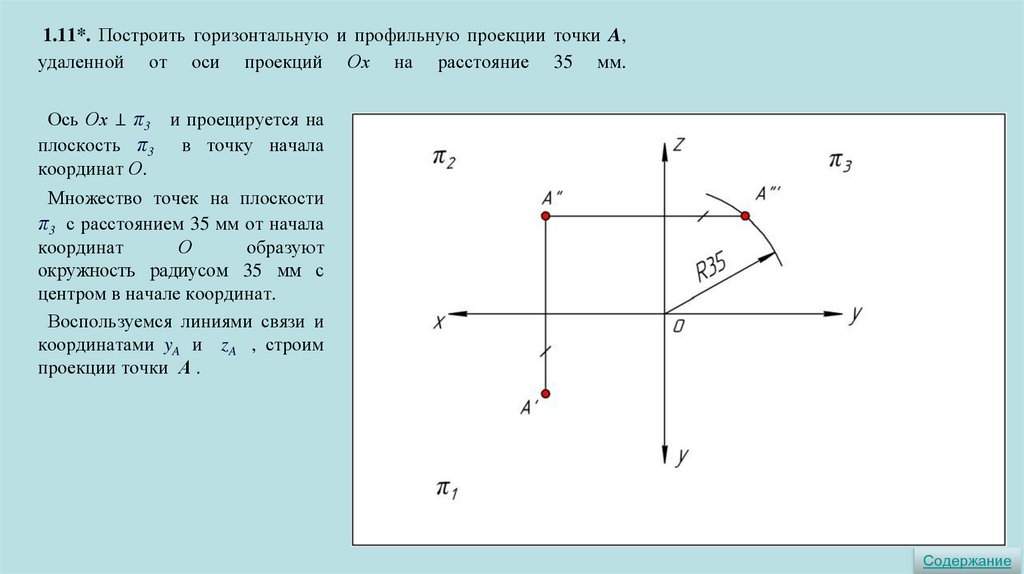
1.11*. Построить горизонтальную и профильную проекции точки A,удаленной от оси проекций Oх на расстояние 35 мм.
Ось Ох ⊥ π3 и проецируется на
плоскость π3 в точку начала
координат О.
Множество точек на плоскости
π3 с расстоянием 35 мм от начала
координат
О
образуют
окружность радиусом 35 мм с
центром в начале координат.
Воспользуемся линиями связи и
координатами yA и zA , строим
проекции точки А .
Содержание
10.
2. ЗАДАНИЕ ПРЯМОЙ ЛИНИИ НА ЧЕРТЕЖЕ2.2. д* Построить проекции отрезка MN. Отрезок MN равен 15 мм и перпендикулярен фронтальной
плоскости проекций
Используя проекции М′ и М′′′ с
помощью линий связи строим
фронтальную проекцию Мʺ конца
отрезка.
Так как отрезок MN ⊥ π2 , то на
плоскость π2 он проецируется в точку
Мʺ ≡ Nʺ.
Из условия, что отрезок MN⊥π2 (MN//π1)
и равен 15 мм, определяем положение
проекции N′( M′N′ =15 мм).
Профильную проекцию точки N′′′
строим, используя координату уN .
Соединяя одноименные проекции точек
М и N, получим проекции отрезка МN.
Содержание
11.
2.2. е* Построить проекции отрезка ST. Точка S отрезка ST лежит на оси Ох.Используя координату у точки Т,
строим горизонтальную проекцию Т′
конца отрезка.
Так как точка S∈Ох, то фронтальная
и горизонтальная проекции точки S
совпадают (Sʺ ≡ S′), а ее профильная
проекция совпадает с началом
координат.
Соединяя одноименные проекции
точек Т и S, получим проекции
отрезка ST.
Содержание
12.
2.6*. Построить проекции прямой d, параллельной прямой а ипересекающей прямые b и с.
Обозначим искомые точки пересечения
прямой d с прямыми b и с:
d ∩ c → M; d ∩ b → K .
Так как M∈d и M∈c, то M’’≡ c’’ (c⊥π2
и проецируется в точку на π2 )
D’’// a’’– строим фронтальную
проекцию прямой d ’’ ;
d ∩ b → K;
Так как К∈d , К∈b, то через К’
строим проекцию d’ (d’// a’ ) → M’.
При решении используем свойство
параллельности прямых.
Содержание
13.
2.8*. Построить проекции прямой с, пересекающей прямые а и b подпрямым углом.
Так как прямая a⊥π1 , то
перпендикулярная к ней прямая с // π1 ,
т.е. горизонтальная прямая. По теореме
о проекциях прямого угла угол между
горизонтальными проекциями с′ и b′ –
прямой.
Фронтальная проекция прямой
сʺ// оси Ох, т.к. прямая с – горизонталь
(с ∩ a → M; с ∩ b → K).
Содержание
14.
2.9*. Построить проекции отрезка BD, перпендикулярного отрезку AC, если точка пересечения этих отрезковделит их пополам, точка B принадлежит фронтальной плоскости проекций, а точка D равноудалена от
плоскостей проекций.
AC – горизонтальная прямая;
BD ⊥ AC; BD ∩ AC → K; AK=KC.
Так как точка B∈π2 , то ее
горизонтальная
проекция
B’∈Ох
(координата yB = 0); BK=KD.
Проекцию точки Dʺ строим из условия,
что yD = zD (равное удаление от π1 и π2 ).
Используя линию связи строим
проекцию Bʺ.
Содержание
15.
3. ЗАДАНИЕ ПЛОСКОСТИ НА ЧЕРТЕЖЕ. ТОЧКА И ПРЯМАЯ В ПЛОСКОСТИ3.4*. Построить недостающие проекции прямых а и b, если прямые а, b, c и точка А лежат в одной плоскости.
Так как прямые принадлежат одной
плоскости, то при пересечении
проекций а′ и с′ получаем
горизонтальную проекцию М′, а затем
фронтальную проекцию Мʺ точки
пересечения прямых а и с и
фронтальную проекцию прямой аʺ.
аʺ∩ bʺ → Kʺ, проекция K′∈ а′.
Проекцию прямой b′ строим
параллельно с′, исходя из условия
задачи и используя свойство
параллельности прямых.
Содержание
16.
4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ4.2*. Достроить горизонтальную проекцию треугольника АВС, плоскость которого параллельна прямой а.
На основании признака
параллельности прямой и плоскости
построим в плоскости, заданной
треугольником АВС, прямую d // a .
Начнем с фронтальной проекции dʺ,
далее M ∈ АС; В∈d .
Содержание
17.
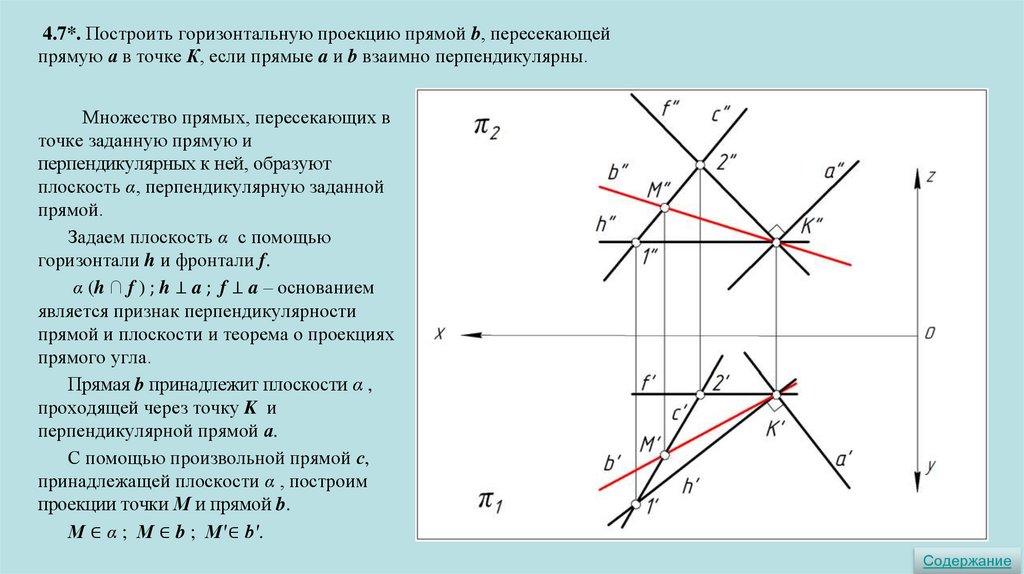
4.7*. Построить горизонтальную проекцию прямой b, пересекающейпрямую а в точке К, если прямые a и b взаимно перпендикулярны.
Множество прямых, пересекающих в
точке заданную прямую и
перпендикулярных к ней, образуют
плоскость α, перпендикулярную заданной
прямой.
Задаем плоскость α с помощью
горизонтали h и фронтали f.
α (h ∩ f ) ; h ⊥ a ; f ⊥ a – основанием
является признак перпендикулярности
прямой и плоскости и теорема о проекциях
прямого угла.
Прямая b принадлежит плоскости α ,
проходящей через точку K и
перпендикулярной прямой а.
С помощью произвольной прямой с,
принадлежащей плоскости α , построим
проекции точки М и прямой b.
М ∈ α ; М ∈ b ; М′∈ b′.
Содержание
18.
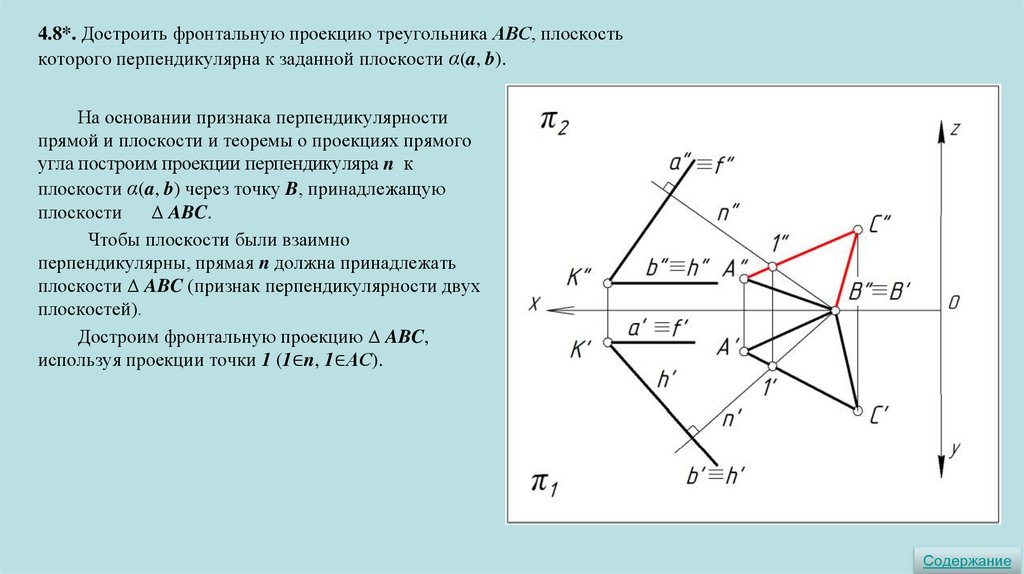
4.8*. Достроить фронтальную проекцию треугольника АВС, плоскостькоторого перпендикулярна к заданной плоскости α(a, b).
На основании признака перпендикулярности
прямой и плоскости и теоремы о проекциях прямого
угла построим проекции перпендикуляра n к
плоскости α(a, b) через точку B, принадлежащую
плоскости
Δ ABC.
Чтобы плоскости были взаимно
перпендикулярны, прямая n должна принадлежать
плоскости Δ ABC (признак перпендикулярности двух
плоскостей).
Достроим фронтальную проекцию Δ ABC,
используя проекции точки 1 (1∈n, 1∈АС).
Содержание
19.
5. ПРОЕКЦИИ МНОГОГРАННИКОВДля решения представленных задач построения проекций многогранников сначала надо
определить расположение плоскостей граней и оснований и положение ребер относительно
плоскостей проекций.
Затем задача сводится к построению проекций отрезков прямых, которые являются либо
боковыми ребрами, либо сторонами оснований многогранников.
Содержание
20.
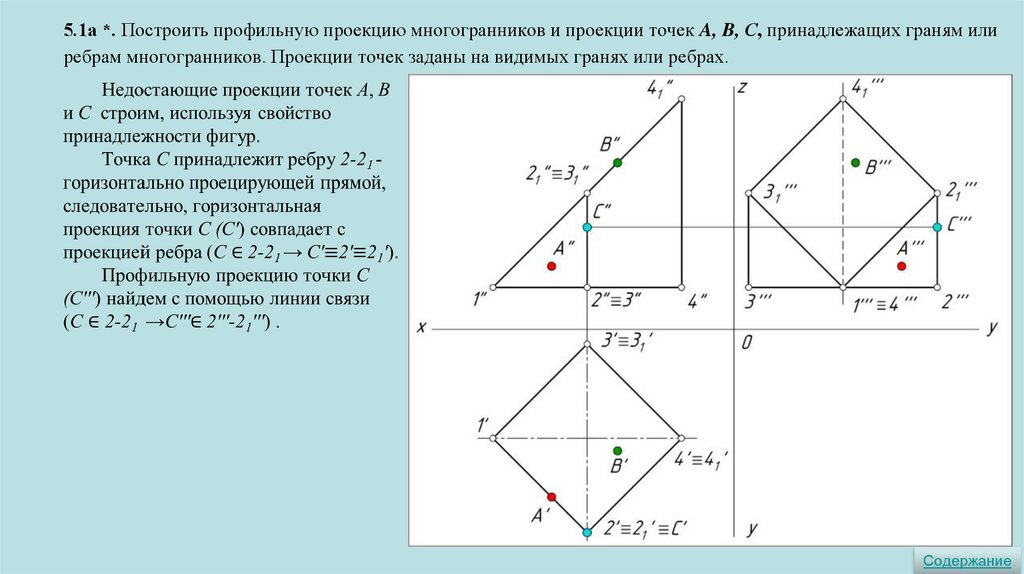
5.1а *. Построить профильную проекцию многогранников и проекции точек A, B, С, принадлежащих граням илиребрам многогранников. Проекции точек заданы на видимых гранях или ребрах.
Верхняя часть прямой
четырёхугольной призмы срезана
фронтально проецирующей плоскостью.
Нижнее основание призмы
параллельно π1, и следовательно
перпендикулярно π2 и π3.
Боковые рёбра принадлежат
горизонтально проецирующим прямым,
следовательно, параллельны плоскостям
π2 и π3.
Боковые грани перпендикулярны π1.
Для построения профильной
проекции используем координаты y и z.
Содержание
21.
5.1а *. Построить профильную проекцию многогранников и проекции точек A, B, С, принадлежащих граням илиребрам многогранников. Проекции точек заданы на видимых гранях или ребрах.
Содержание
22.
5.1а *. Построить профильную проекцию многогранников и проекции точек A, B, С, принадлежащих граням илиребрам многогранников. Проекции точек заданы на видимых гранях или ребрах.
Содержание
23.
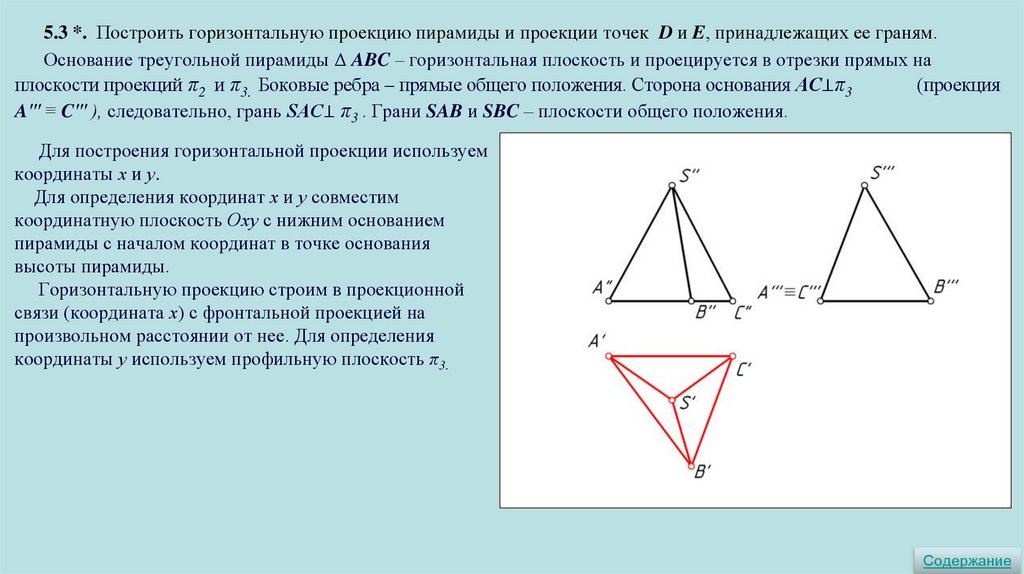
5.3 *. Построить горизонтальную проекцию пирамиды и проекции точек D и E, принадлежащих ее граням.Основание треугольной пирамиды Δ ABC – горизонтальная плоскость и проецируется в отрезки прямых на
плоскости проекций π2 и π3. Боковые ребра – прямые общего положения. Сторона основания АС⊥π3
(проекция
A′′′ ≡ C′′′ ), следовательно, грань SАС⊥ π3 . Грани SAB и SBC – плоскости общего положения.
Для построения горизонтальной проекции используем
координаты х и у.
Для определения координат х и у совместим
координатную плоскость Оху с нижним основанием
пирамиды с началом координат в точке основания
высоты пирамиды.
Горизонтальную проекцию строим в проекционной
связи (координата х) с фронтальной проекцией на
произвольном расстоянии от нее. Для определения
координаты у используем профильную плоскость π3.
Содержание
24.
5.3 *. Построить горизонтальную проекцию пирамиды и проекции точек D и E, принадлежащих ее граням.Основание треугольной пирамиды Δ ABC – горизонтальная плоскость и проецируется в отрезки прямых на
плоскости проекций π2 и π3. Боковые ребра – прямые общего положения. Сторона основания АС⊥π3
(проекция
A′′′ ≡ C′′′ ), следовательно, грань SАС⊥ π3 . Грани SAB и SBC – плоскости общего положения.
Для построения горизонтальной проекции используем
координаты х и у.
Для определения координат х и у совместим
координатную плоскость Оху с нижним основанием
пирамиды с началом координат в основании высоты
пирамиды.
Горизонтальную проекцию строим в проекционной
связи (координата х) с фронтальной проекцией на
произвольном расстоянии от нее. Для определения
координаты у используем профильную плоскость π3.
Проекции точек: D ∈ SBC; E ∈ SAB.
Проекции точек, принадлежащих плоскостям общего
положения, построим с помощью прямых линий,
принадлежащих этим плоскостям.
Так как стороны основания пирамиды являются
горизонталями для боковых граней, то для построения
проекций точек удобно воспользоваться горизонталями
плоскостей SAB и SBC, проходящими через точки D и E
.
Содержание
25.
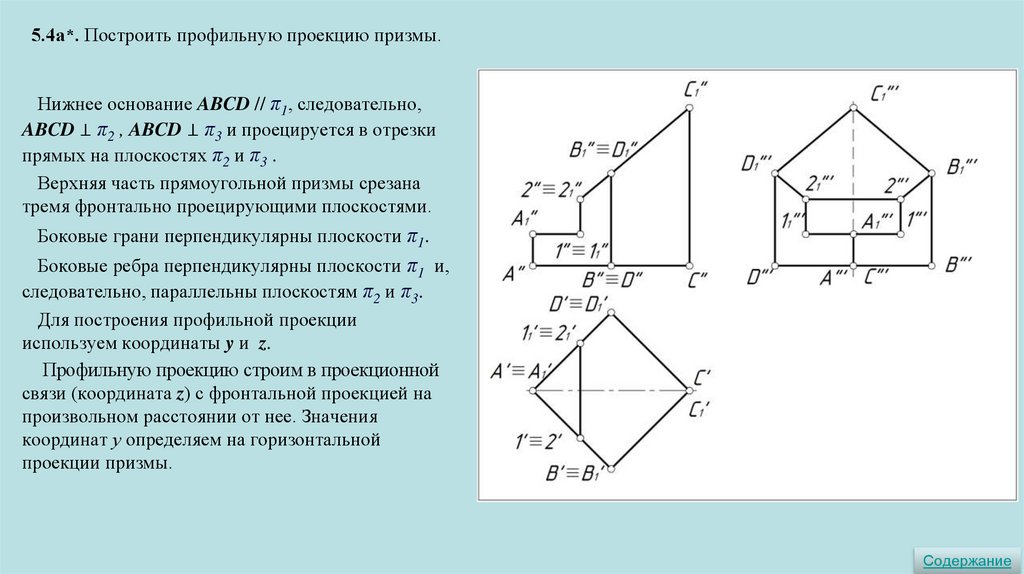
5.4а*. Построить профильную проекцию призмы.Нижнее основание ABCD // π1, следовательно,
ABCD ⊥ π2 , ABCD ⊥ π3 и проецируется в отрезки
прямых на плоскостях π2 и π3 .
Верхняя часть прямоугольной призмы срезана
тремя фронтально проецирующими плоскостями.
Боковые грани перпендикулярны плоскости π1.
Боковые ребра перпендикулярны плоскости π1 и,
следовательно, параллельны плоскостям π2 и π3.
Для построения профильной проекции
используем координаты y и z.
Профильную проекцию строим в проекционной
связи (координата z) с фронтальной проекцией на
произвольном расстоянии от нее. Значения
координат у определяем на горизонтальной
проекции призмы.
Содержание
26.
6. СПОСОБЫ ПРЕОБРАЗОВАНИЯ. МЕТРИЧЕСКИЕ ЗАДАЧИСпособ замены плоскостей проекций
6.1*. Построить проекции отрезка АВ=30 мм, принадлежащего прямой а, применив способ
замены плоскостей проекций.
Содержание
27.
6.2 *. Построить проекции перпендикуляра, опущенного из точки А на прямую b. Применить прирешении способ замены плоскостей проекций.
Содержание
28.
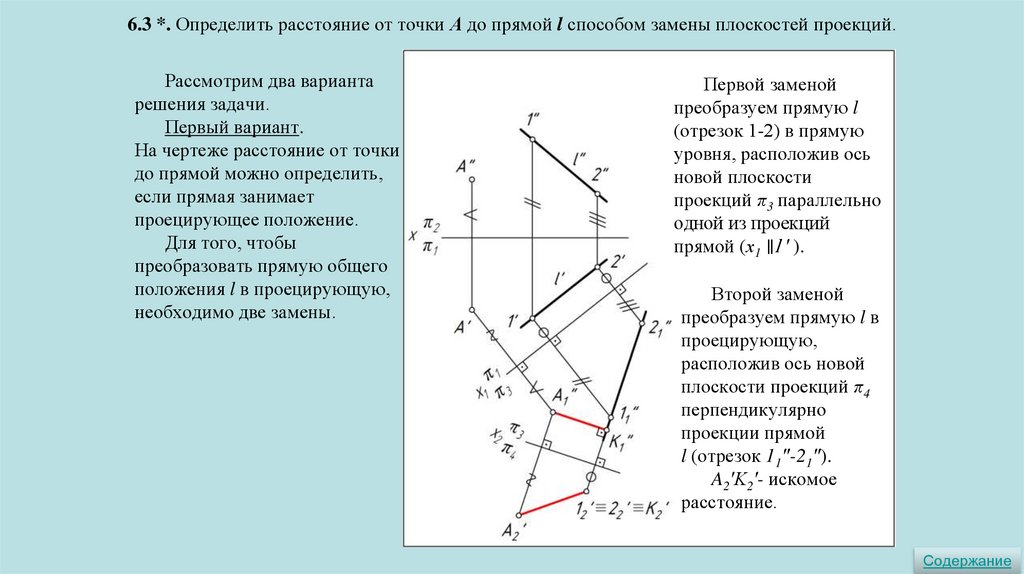
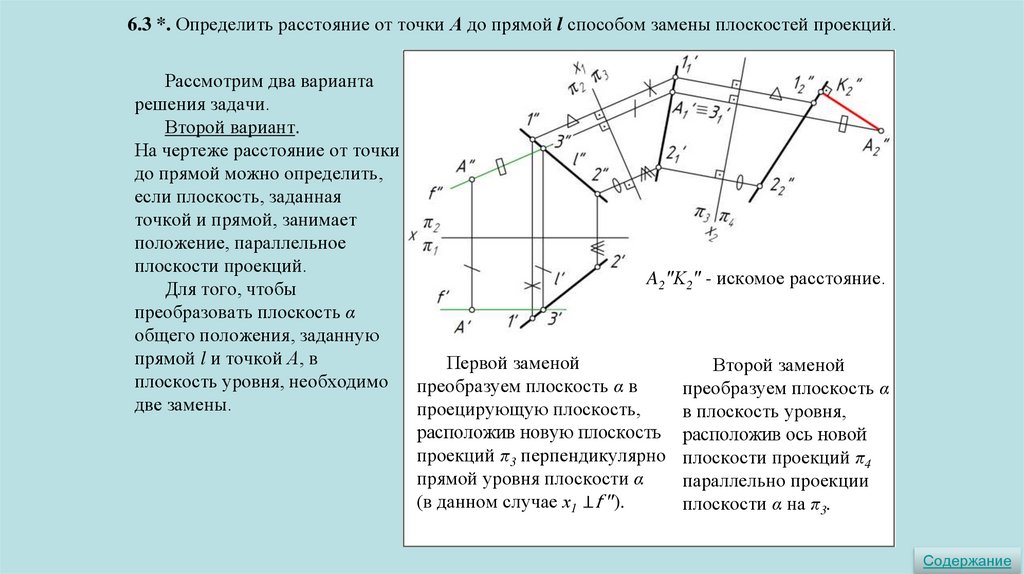
6.3 *. Определить расстояние от точки А до прямой l способом замены плоскостей проекций.Рассмотрим два варианта
решения задачи.
Первый вариант.
На чертеже расстояние от точки
до прямой можно определить,
если прямая занимает
проецирующее положение.
Для того, чтобы
преобразовать прямую общего
положения l в проецирующую,
необходимо две замены.
Первой заменой
преобразуем прямую l
(отрезок 1-2) в прямую
уровня, расположив ось
новой плоскости
проекций π3 параллельно
одной из проекций
прямой (х1 ∥l ′ ).
Второй заменой
преобразуем прямую l в
проецирующую,
расположив ось новой
плоскости проекций π4
перпендикулярно
проекции прямой
l (отрезок 11ʺ-21ʺ).
A2′K2′- искомое
расстояние.
Содержание
29.
6.3 *. Определить расстояние от точки А до прямой l способом замены плоскостей проекций.Рассмотрим два варианта
решения задачи.
Второй вариант.
На чертеже расстояние от точки
до прямой можно определить,
если плоскость, заданная
точкой и прямой, занимает
положение, параллельное
плоскости проекций.
A2ʺK2ʺ - искомое расстояние.
Для того, чтобы
преобразовать плоскость α
общего положения, заданную
прямой l и точкой А, в
Первой заменой
Второй заменой
плоскость уровня, необходимо преобразуем плоскость α в
преобразуем плоскость α
две замены.
проецирующую плоскость,
в плоскость уровня,
расположив новую плоскость расположив ось новой
проекций π3 перпендикулярно плоскости проекций π4
прямой уровня плоскости α
параллельно проекции
(в данном случае х1 ⊥f ʺ).
плоскости α на π3.
Содержание
30.
6.5 *. Определить расстояние от точки А до плоскости α(АВС), применив способзамены плоскостей проекций. Построить проекции отрезка, определяющего это
расстояние.
На чертеже расстояние от
Фронтальную
точки до плоскости можно
проекцию точки К (Кʺ)
определить, если плоскость
определим с помощью
занимает проецирующее
координаты z.
положение.
Горизонтальная
Одно преобразование
проекция A′K′⊥C′D′
необходимо, чтобы плоскость
(признак
общего положения перевести в
перпендикулярности
положение, перпендикулярное
прямой и плоскости и
плоскости проекций.
теорема о проекциях
Выполним замену плоскостей
прямого угла ).
проекций, используя линию
уровня плоскости общего
положения. В данной задаче
используем горизонталь CD.
Новая ось проекций x1⊥C′D′.
Плоскость ΔBCD
спроецируется в прямую линию
на новую плоскость проекций π3.
Искомое расстояние – отрезок
А1ʺК1ʺ.
Построим проекции перпендикуляра в исходной системе плоскостей.
Содержание
31.
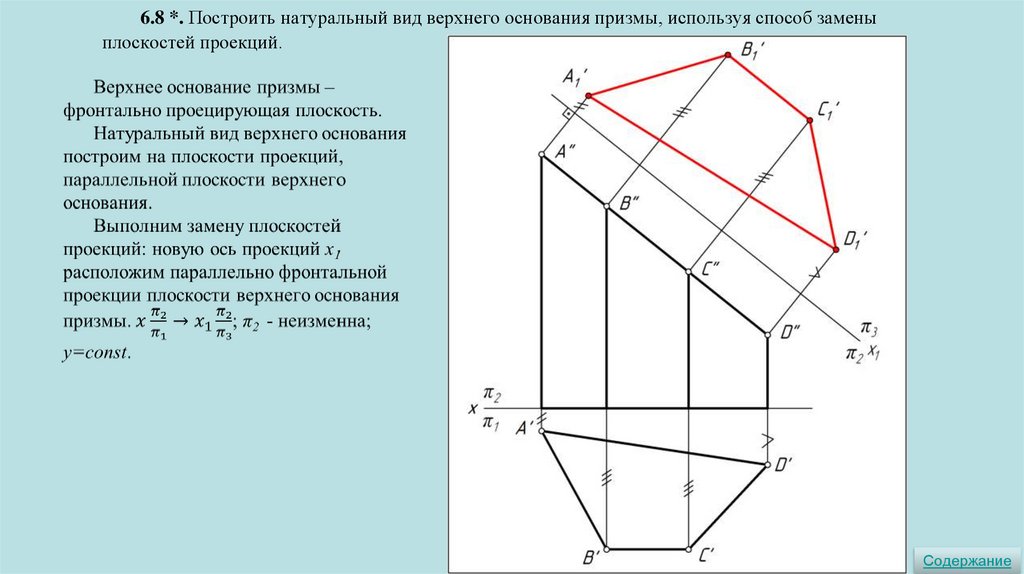
6.8 *. Построить натуральный вид верхнего основания призмы, используя способ заменыплоскостей проекций.
Содержание
32.
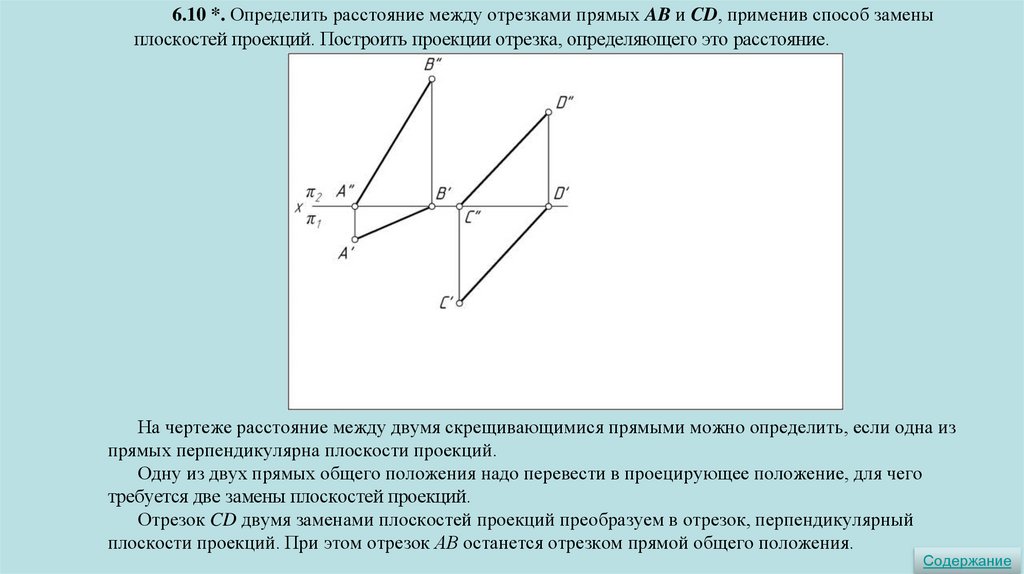
6.10 *. Определить расстояние между отрезками прямых AB и CD, применив способ заменыплоскостей проекций. Построить проекции отрезка, определяющего это расстояние.
На чертеже расстояние между двумя скрещивающимися прямыми можно определить, если одна из
прямых перпендикулярна плоскости проекций.
Одну из двух прямых общего положения надо перевести в проецирующее положение, для чего
требуется две замены плоскостей проекций.
Отрезок CD двумя заменами плоскостей проекций преобразуем в отрезок, перпендикулярный
плоскости проекций. При этом отрезок АВ останется отрезком прямой общего положения.
Содержание
33.
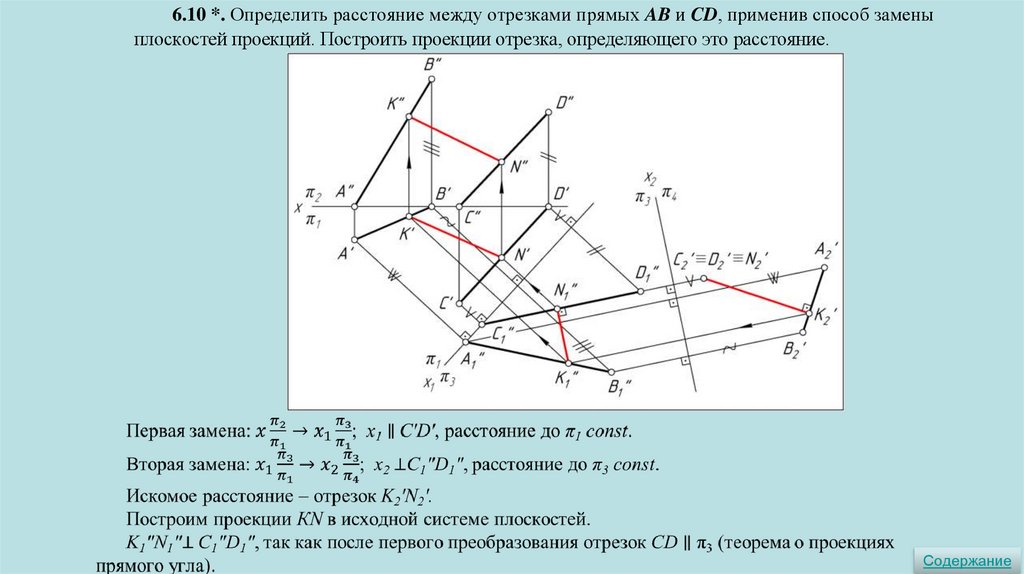
6.10 *. Определить расстояние между отрезками прямых AB и CD, применив способ заменыплоскостей проекций. Построить проекции отрезка, определяющего это расстояние.
Содержание
34.
Способ плоскопараллельного перемещения6.11 *. С помощью плоскопараллельного перемещения построить проекции отрезка АB=20 мм
на прямой a.
Отрезок прямой проецируется без
искажений на плоскость проекций, если
прямая параллельна плоскости проекций.
При этом одна проекция прямой (отрезка)
параллельна оси проекций.
Чтобы прямая общего положения заняла
положение, параллельное плоскости
проекций, надо выполнить одно
преобразование.
На прямой а зададим произвольную
точку С.
Плоскопараллельным движением относительно горизонтальной плоскости проекций переместим
отрезок АС в положение параллельное фронтальной плоскости проекций (при этом А1′С1′ ∥ х).
При этом А1ʺС1ʺ - натуральная величина отрезка АС.
Отложив 20 мм (А1ʺВ1ʺ = 20 мм), получим проекцию точки В (В1ʺ).
Переместив отрезок плоскопараллельным движением (параллельно π1) в исходное положение,
получим проекции отрезка (Аʺ1ʺ и А′В′) длиной 20 мм.
Задача решается аналогично, если перемещать отрезок параллельно фронтальной плоскости
проекций.
Содержание
35.
6.12 *. Определитьрасстояние от точки А до прямой l
способом плоскопараллельного
перемещения.
На чертеже расстояние от точки до
прямой можно определить, если
прямая занимает проецирующее
положение.
Для того, чтобы преобразовать
прямую общего положения l в
проецирующую прямую, необходимо
два преобразования:
Искомое расстояние – отрезок А2ʺK2ʺ
1) преобразуем прямую l (отрезок ВС) в прямую уровня. Для этого переместим отрезок ВС
параллельно фронтальной плоскости проекций до положения, когда он будет параллелен
горизонтальной плоскости (В1ʺС1ʺ ∥ х), перемещаем также точку А;
2) преобразуем прямую l (отрезок ВС) в проецирующую прямую. Для этого переместим отрезок ВС
параллельно горизонтальной плоскости проекций до положения, когда он будет перпендикулярен
фронтальной плоскости (В2′С2′ ⊥ х), перемещаем и точку А.
Второй вариант решения задачи (аналогично задаче 6.3) - плоскость, заданную точкой А и
прямой l, нужно преобразовать в плоскость уровня.
Содержание
36.
6.13 *. Определить расстояние от точки А до плоскости, заданной двумя пересекающимися прямыми,способом плоскопараллельного перемещения.
На чертеже расстояние от точки до
плоскости можно определить, если
плоскость занимает проецирующее
положение.
Одно преобразование необходимо,
чтобы плоскость общего положения
перевести в положение,
перпендикулярное плоскости проекций.
В данной задаче используем
горизонталь 1-2.
Плоскопараллельным движением относительно горизонтальной плоскости проекций переместим
плоскость α (a,b) так, чтобы её горизонталь 1-2 заняла положение, перпендикулярное плоскости π2.
Перемещаем также точку А. В этом положении плоскость α (a,b)⊥π2 (признак перпендикулярности
двух плоскостей).
Искомое расстояние – отрезок А1ʺN1ʺ .
Задачу можно решить аналогично с использованием фронтали.
Содержание
37.
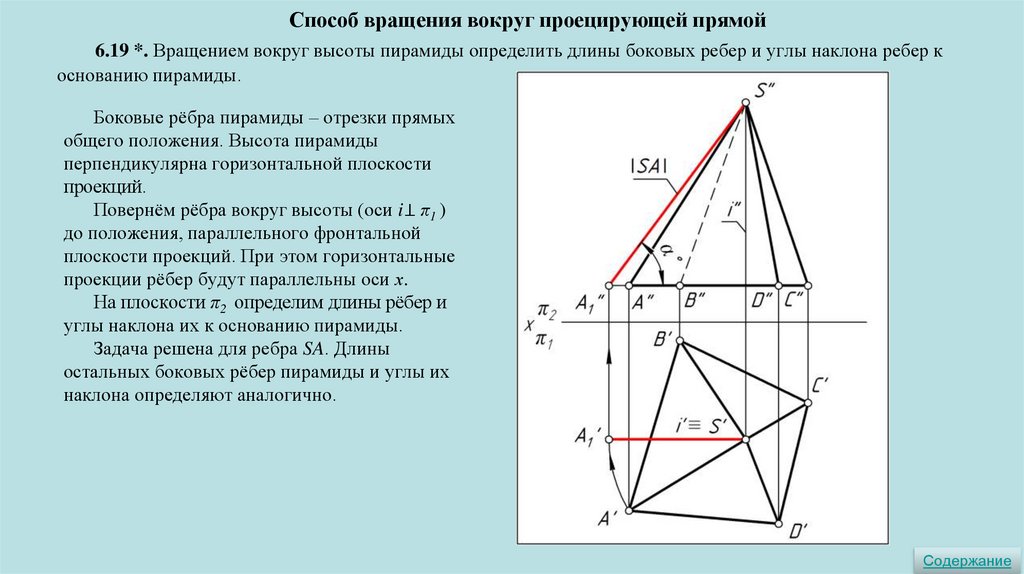
Способ вращения вокруг проецирующей прямой6.19 *. Вращением вокруг высоты пирамиды определить длины боковых ребер и углы наклона ребер к
основанию пирамиды.
Боковые рёбра пирамиды – отрезки прямых
общего положения. Высота пирамиды
перпендикулярна горизонтальной плоскости
проекций.
Повернём рёбра вокруг высоты (оси i⊥ π1 )
до положения, параллельного фронтальной
плоскости проекций. При этом горизонтальные
проекции рёбер будут параллельны оси х.
На плоскости π2 определим длины рёбер и
углы наклона их к основанию пирамиды.
Задача решена для ребра SA. Длины
остальных боковых рёбер пирамиды и углы их
наклона определяют аналогично.
Содержание
38.
Композиция преобразований6.20 *. Определить угол φ между прямой с и плоскостью α(a ⋂ b), применив способ
плоскопараллельного перемещения и способ замены плоскостей проекций.
На прямой с зададим произвольную точку К.
Из точки К опустим перпендикуляр n на плоскость α(a ⋂ b).
Содержание
39.
Композиция преобразований6.20 *. Определить угол φ между прямой с и плоскостью α(a ⋂ b), применив способ
плоскопараллельного перемещения и способ замены плоскостей проекций.
Определим величину угла ψ, образованного прямыми с и n:
1) способом плоскопараллельного перемещения преобразуем плоскость общего
положения γ(с ⋂ n) в проецирующую, перпендикулярную π2, используя горизонталь h.
Содержание
40.
Композиция преобразований6.20 *. Определить угол φ между прямой с и плоскостью α(a ⋂ b), применив способ
плоскопараллельного перемещения и способ замены плоскостей проекций.
2) способом замены плоскостей проекций расположим фронтально проецирующую
плоскость γ(с ⋂ n) параллельно новой плоскости проекций π3.
Определим величину угла ψ. Искомый угол φ будет дополнительным до 90° к углу ψ.
Содержание
41.
6.22 *. Определить угол φ между плоскостями α(ABC) и β(a ⋂ b), применив способплоскопараллельного перемещения и вращение вокруг проецирующей прямой
Из произвольно выбранной точки К опустим перпендикуляры n и l на плоскости
β(a ⋂ b) и α(ABC) соответственно.
Содержание
42.
6.22 *. Определить угол φ между плоскостями α(ABC) и β(a ⋂ b), применив способплоскопараллельного перемещения и вращение вокруг проецирующей прямой
Определим величину угла ψ, образованного перпендикулярами n и l:
1) способом плоскопараллельного перемещения преобразуем плоскость общего
положения γ(n ⋂ l) в проецирующую, перпендикулярную π1, используя фронталь f ;
2) вращением вокруг проецирующей прямой i≡f расположим плоскость γ(n ⋂ l)
параллельно плоскости проекций π2.
Определим величину угла ψ. Искомый угол φ будет дополнительным до 180° к углу ψ.
Содержание
43.
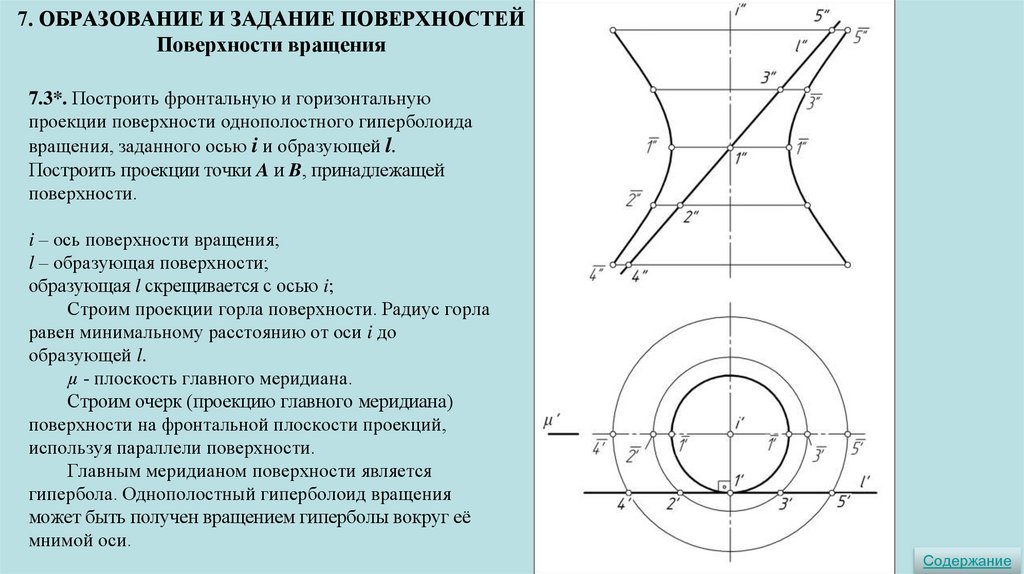
7. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТЕЙПоверхности вращения
7.3*. Построить фронтальную и горизонтальную
проекции поверхности однополостного гиперболоида
вращения, заданного осью i и образующей l.
Построить проекции точки A и B, принадлежащей
поверхности.
i – ось поверхности вращения;
l – образующая поверхности;
образующая l скрещивается с осью i;
Строим проекции горла поверхности. Радиус горла
равен минимальному расстоянию от оси i до
образующей l.
µ - плоскость главного меридиана.
Строим очерк (проекцию главного меридиана)
поверхности на фронтальной плоскости проекций,
используя параллели поверхности.
Главным меридианом поверхности является
гипербола. Однополостный гиперболоид вращения
может быть получен вращением гиперболы вокруг её
мнимой оси.
Содержание
44.
Однополостный гиперболоид вращения имеет двасемейства прямолинейных образующих –
последовательных положений образующей l и
симметричной ей прямой k.
Построим образующую первого семейства в
следующем положении l1 при вращении вокруг оси i.
Построим образующую второго семейства в двух
положениях k и k1. симметрично l и l1 относительно оси.
Образующие одного семейства между собой не
пересекаются, а образующие разных семейств
пересекаются.
Вдоль оси поверхность гиперболоида бесконечна.
Ограничим поверхность гиперболоида сверху и снизу
произвольными параллелями.
Содержание
45.
Построим недостающие проекции точек, принадлежащихповерхности однополостного гиперболоида вращения.
Для построения горизонтальной проекции точки А можно
воспользоваться только параллелью.
Для построения фронтальной проекции точки В можно
воспользоваться параллелью или образующей.
Содержание
46.
Винтовая поверхность7.4*. Построить фронтальную и горизонтальную проекции
поверхности правого косого закрытого геликоида с осью i,
образующей АВ и ходом Ph . Построить недостающие
проекции точек М и К, принадлежащих поверхности.
При вращении образующей вокруг оси получается
коническая поверхность с углом при вершине 2α°
(направляющий конус).
Если образующая вращается и одновременно
перемещается вдоль оси, то в каждом положении
образующие gi параллельны соответствующим образующим
направляющего соосного конуса.
При сечении этой поверхности плоскостью,
перпендикулярной оси i, получается кривая - спираль
Архимеда. Поверхность называется Архимедов винт.
Построим горизонтальную проекцию точки К,
используя спираль Архимеда.
Построим горизонтальную проекцию точки М,
используя образующую.
Содержание
47.
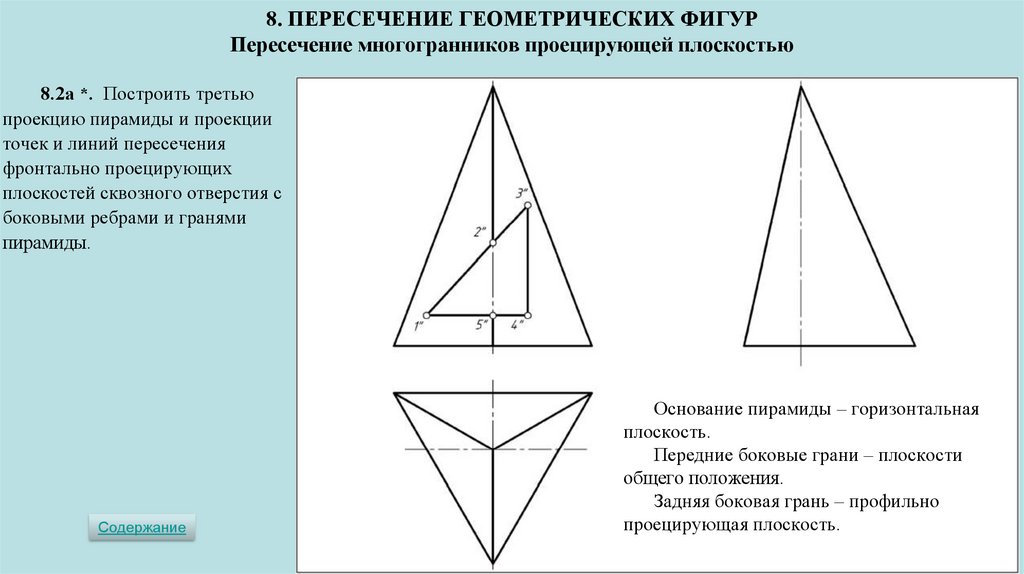
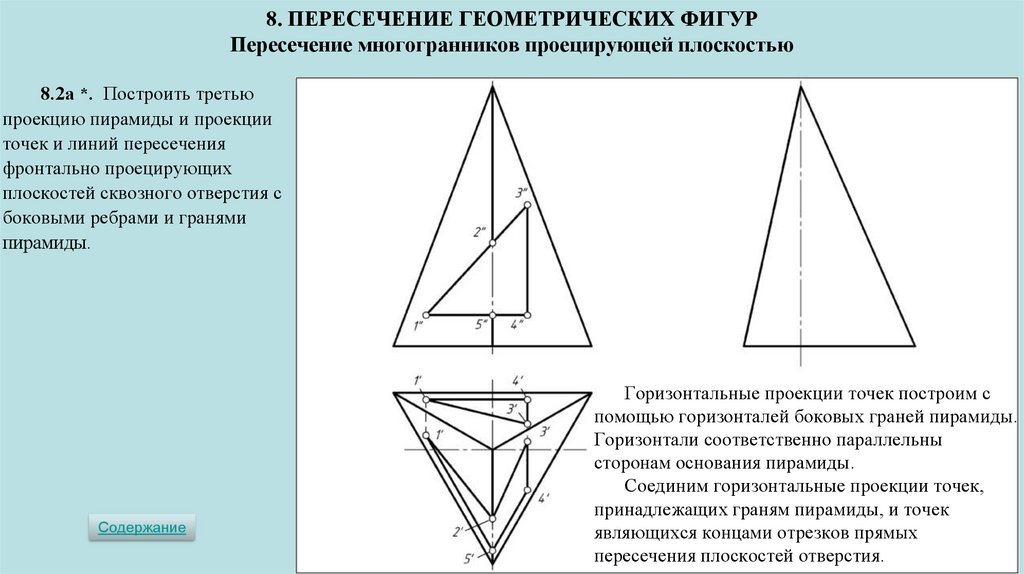
8. ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУРПересечение многогранников проецирующей плоскостью
8.2а *. Построить третью
проекцию пирамиды и проекции
точек и линий пересечения
фронтально проецирующих
плоскостей сквозного отверстия с
боковыми ребрами и гранями
пирамиды.
Содержание
Основание пирамиды – горизонтальная
плоскость.
Передние боковые грани – плоскости
общего положения.
Задняя боковая грань – профильно
проецирующая плоскость.
48.
8. ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУРПересечение многогранников проецирующей плоскостью
8.2а *. Построить третью
проекцию пирамиды и проекции
точек и линий пересечения
фронтально проецирующих
плоскостей сквозного отверстия с
боковыми ребрами и гранями
пирамиды.
Содержание
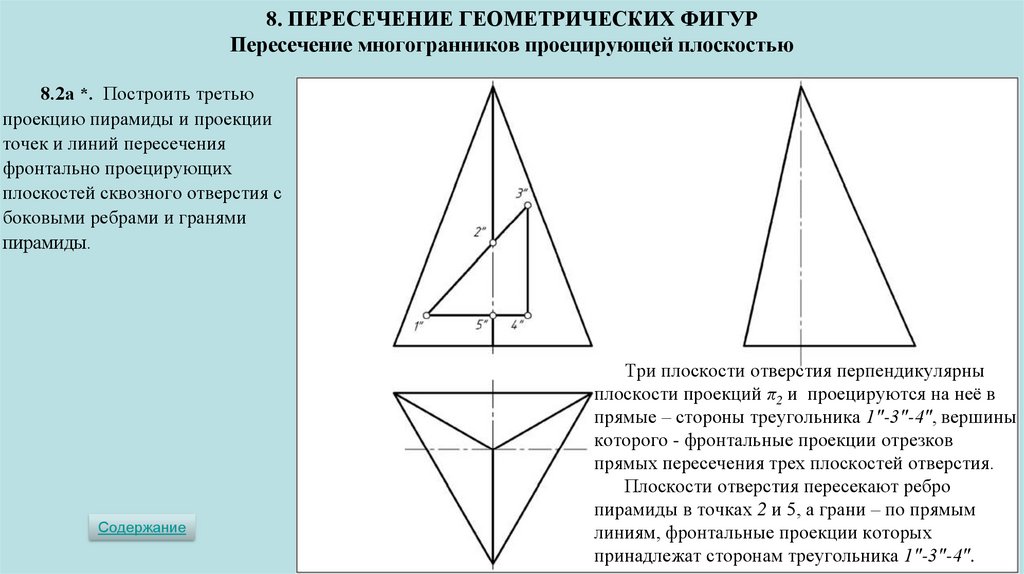
Три плоскости отверстия перпендикулярны
плоскости проекций π2 и проецируются на неё в
прямые – стороны треугольника 1ʺ-3ʺ-4ʺ, вершины
которого - фронтальные проекции отрезков
прямых пересечения трех плоскостей отверстия.
Плоскости отверстия пересекают ребро
пирамиды в точках 2 и 5, а грани – по прямым
линиям, фронтальные проекции которых
принадлежат сторонам треугольника 1ʺ-3ʺ-4ʺ.
49.
8. ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУРПересечение многогранников проецирующей плоскостью
8.2а *. Построить третью
проекцию пирамиды и проекции
точек и линий пересечения
фронтально проецирующих
плоскостей сквозного отверстия с
боковыми ребрами и гранями
пирамиды.
Содержание
Горизонтальные проекции точек построим с
помощью горизонталей боковых граней пирамиды.
Горизонтали соответственно параллельны
сторонам основания пирамиды.
Соединим горизонтальные проекции точек,
принадлежащих граням пирамиды, и точек
являющихся концами отрезков прямых
пересечения плоскостей отверстия.
50.
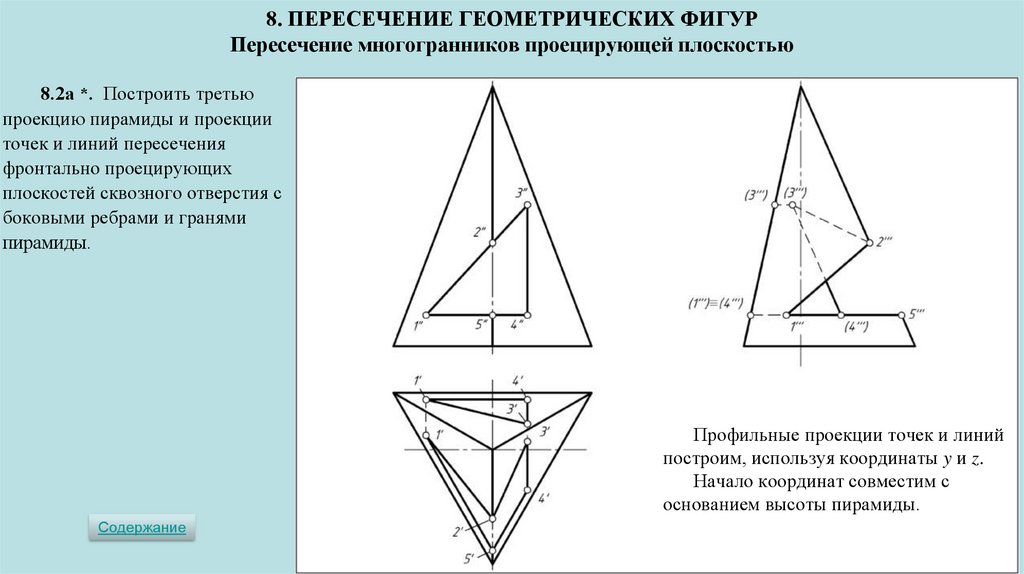
8. ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУРПересечение многогранников проецирующей плоскостью
8.2а *. Построить третью
проекцию пирамиды и проекции
точек и линий пересечения
фронтально проецирующих
плоскостей сквозного отверстия с
боковыми ребрами и гранями
пирамиды.
Профильные проекции точек и линий
построим, используя координаты y и z.
Начало координат совместим с
основанием высоты пирамиды.
Содержание
51.
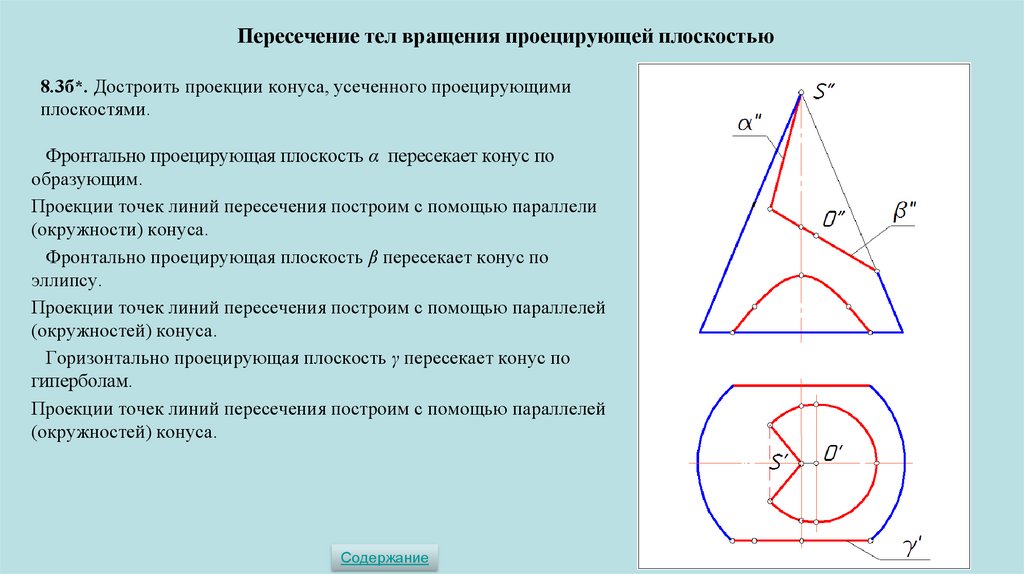
Пересечение тел вращения проецирующей плоскостью8.3б*. Достроить проекции конуса, усеченного проецирующими
плоскостями.
Фронтально проецирующая плоскость α пересекает конус по
образующим.
Проекции точек линий пересечения построим с помощью параллели
(окружности) конуса.
Фронтально проецирующая плоскость β пересекает конус по
эллипсу.
Проекции точек линий пересечения построим с помощью параллелей
(окружностей) конуса.
Горизонтально проецирующая плоскость γ пересекает конус по
гиперболам.
Проекции точек линий пересечения построим с помощью параллелей
(окружностей) конуса.
Содержание
52.
8.3 в*. Достроить проекции конуса, усеченного проецирующимиплоскостями.
Фронтально проецирующая плоскость α пересекает конус по
окружности.
Проекцию линии пересечения построим с помощью параллели
(окружности) конуса.
Фронтально проецирующая плоскость β пересекает конус по
параболе.
Проекции точек линий пересечения построим с помощью
параллелей (окружностей) конуса.
Содержание
53.
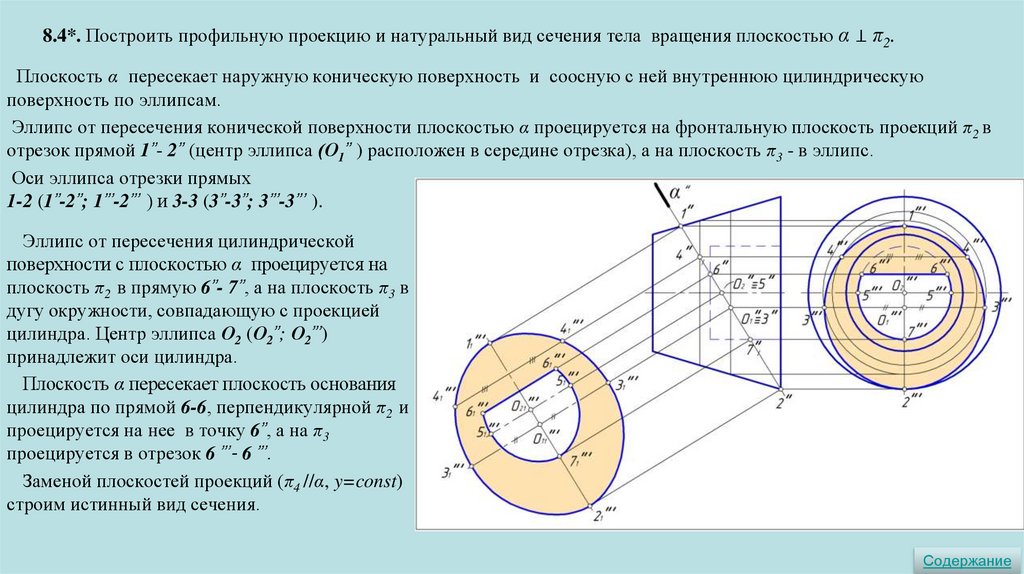
8.4*. Построить профильную проекцию и натуральный вид сечения тела вращения плоскостью α ⊥ π2.Плоскость α пересекает наружную коническую поверхность и соосную с ней внутреннюю цилиндрическую
поверхность по эллипсам.
Эллипс от пересечения конической поверхности плоскостью α проецируется на фронтальную плоскость проекций π2 в
отрезок прямой 1”- 2” (центр эллипса (О1” ) расположен в середине отрезка), а на плоскость π3 - в эллипс.
Оси эллипса отрезки прямых
1-2 (1”-2”; 1”’-2”’ ) и 3-3 (3”-3”; 3”’-3”’ ).
Эллипс от пересечения цилиндрической
поверхности с плоскостью α проецируется на
плоскость π2 в прямую 6”- 7”, а на плоскость π3 в
дугу окружности, совпадающую с проекцией
цилиндра. Центр эллипса О2 (О2”; О2”’)
принадлежит оси цилиндра.
Плоскость α пересекает плоскость основания
цилиндра по прямой 6-6, перпендикулярной π2 и
проецируется на нее в точку 6”, а на π3
проецируется в отрезок 6 ”’- 6 ”’.
Заменой плоскостей проекций (π4 //α, y=const)
строим истинный вид сечения.
Содержание
54.
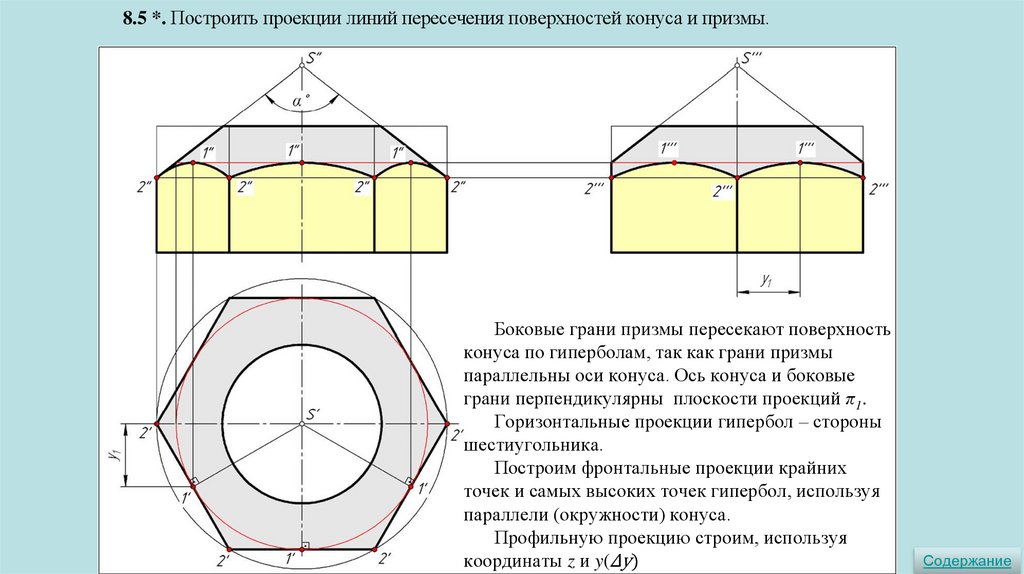
8.5 *. Построить проекции линий пересечения поверхностей конуса и призмы.Боковые грани призмы пересекают поверхность
конуса по гиперболам, так как грани призмы
параллельны оси конуса. Ось конуса и боковые
грани перпендикулярны плоскости проекций π1.
Горизонтальные проекции гипербол – стороны
шестиугольника.
Построим фронтальные проекции крайних
точек и самых высоких точек гипербол, используя
параллели (окружности) конуса.
Профильную проекцию строим, используя
координаты z и y(Δy)
Содержание
55.
Пересечение прямой и плоскости, двух плоскостей8.9*. Через точку А построить проекции прямой, пересекающей прямую а под прямым углом.
Прямая, перпендикулярная прямой общего
положения a, будет также прямой общего
положения. Прямой угол между ними
проецируется с искажением на плоскости
проекций.
Воспользуемся плоскостью α ⊥ а, как
множеством прямых, проходящих через точку А
и перпендикулярных прямой а.
Зададим плоскость α горизонталью h и
фронталью f.
Заключим прямую а в проецирующую
плоскость γ ⊥ π2.
Плоскость γ ∩ α (h, f ) по прямой 1 -2.
Прямая а ∩ 1- 2 в точке К.
Построим проекции прямой АК, пересекающей
прямую а под прямым углом и проходящей
через точку А.
Содержание
56.
Пересечение прямой линии и поверхности8.14*. Построить проекции точек пересечения прямой a со сферой,
используя способ замены плоскостей проекций.
Содержание
57.
8.15*. Построить проекции точек пересечения прямой a с поверхностью тора,применив способ вращения вокруг проецирующей прямой.
Ось вращения i тора перпендикулярна плоскости π1.
Прямая а пересекает ось вращения i в точке А.
Точка А ∈ i , неподвижна.
Повернем прямую а вокруг оси тора до ее совмещения
с плоскостью окружности m.
Для этого возьмем на прямой а произвольно точку М.
Определим проекции точек пересечения прямой а1 и
окружности m – точки 11 и 21 .
Повернув прямую в первоначальное положение
получим искомые проекции точек пересечения 1 и 2.
Содержание
58.
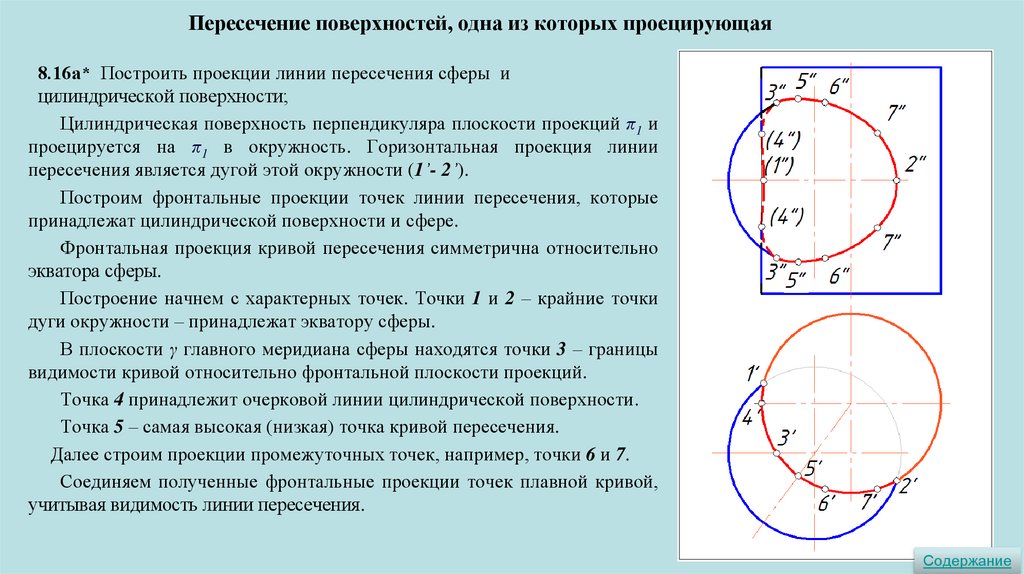
Пересечение поверхностей, одна из которых проецирующая8.16а* Построить проекции линии пересечения сферы и
цилиндрической поверхности;
Цилиндрическая поверхность перпендикуляра плоскости проекций π1 и
проецируется на π1 в окружность. Горизонтальная проекция линии
пересечения является дугой этой окружности (1’- 2’).
Построим фронтальные проекции точек линии пересечения, которые
принадлежат цилиндрической поверхности и сфере.
Фронтальная проекция кривой пересечения симметрична относительно
экватора сферы.
Построение начнем с характерных точек. Точки 1 и 2 – крайние точки
дуги окружности – принадлежат экватору сферы.
В плоскости γ главного меридиана сферы находятся точки 3 – границы
видимости кривой относительно фронтальной плоскости проекций.
Точка 4 принадлежит очерковой линии цилиндрической поверхности.
Точка 5 – самая высокая (низкая) точка кривой пересечения.
Далее строим проекции промежуточных точек, например, точки 6 и 7.
Соединяем полученные фронтальные проекции точек плавной кривой,
учитывая видимость линии пересечения.
Содержание
59.
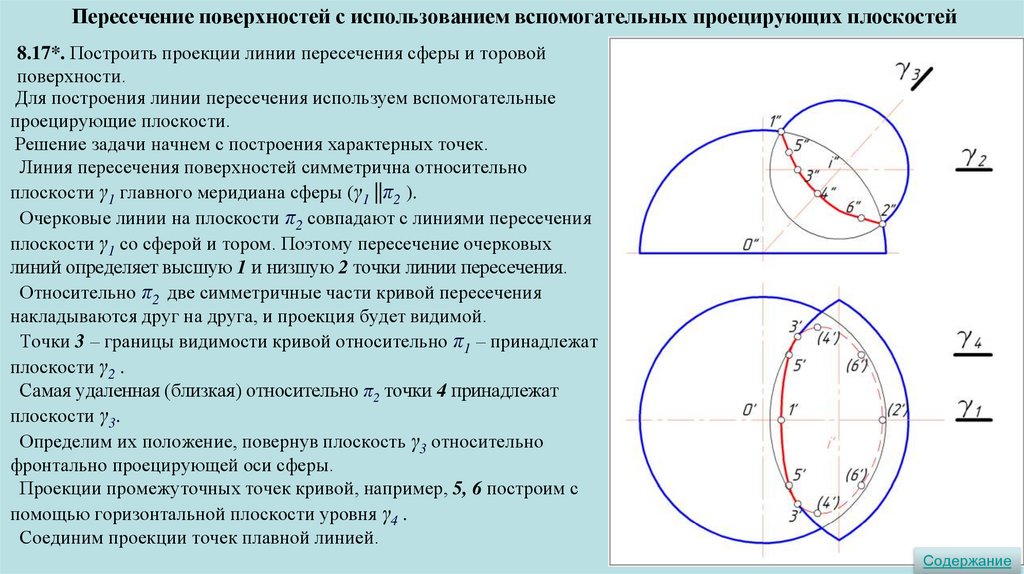
Пересечение поверхностей с использованием вспомогательных проецирующих плоскостей8.17*. Построить проекции линии пересечения сферы и торовой
поверхности.
Для построения линии пересечения используем вспомогательные
проецирующие плоскости.
Решение задачи начнем с построения характерных точек.
Линия пересечения поверхностей симметрична относительно
плоскости γ1 главного меридиана сферы (γ1 ||π2 ).
Очерковые линии на плоскости π2 совпадают с линиями пересечения
плоскости γ1 со сферой и тором. Поэтому пересечение очерковых
линий определяет высшую 1 и низшую 2 точки линии пересечения.
Относительно π2 две симметричные части кривой пересечения
накладываются друг на друга, и проекция будет видимой.
Точки 3 – границы видимости кривой относительно π1 – принадлежат
плоскости γ2 .
Самая удаленная (близкая) относительно π2 точки 4 принадлежат
плоскости γ3.
Определим их положение, повернув плоскость γ3 относительно
фронтально проецирующей оси сферы.
Проекции промежуточных точек кривой, например, 5, 6 построим с
помощью горизонтальной плоскости уровня γ4 .
Соединим проекции точек плавной линией.
Содержание
60.
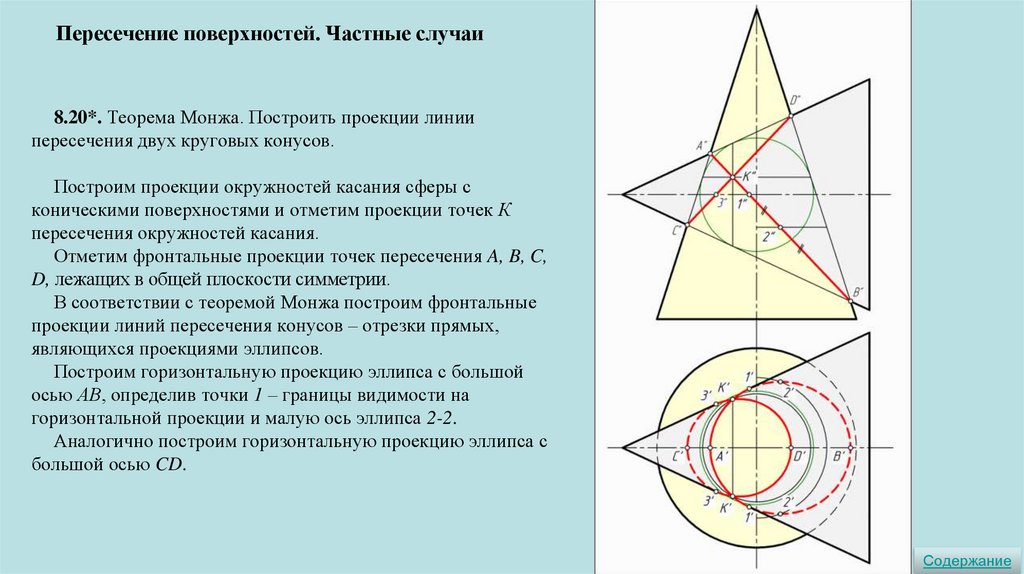
Пересечение поверхностей. Частные случаи8.20*. Теорема Монжа. Построить проекции линии
пересечения двух круговых конусов.
Построим проекции окружностей касания сферы с
коническими поверхностями и отметим проекции точек К
пересечения окружностей касания.
Отметим фронтальные проекции точек пересечения A, B, C,
D, лежащих в общей плоскости симметрии.
В соответствии с теоремой Монжа построим фронтальные
проекции линий пересечения конусов – отрезки прямых,
являющихся проекциями эллипсов.
Построим горизонтальную проекцию эллипса с большой
осью АВ, определив точки 1 – границы видимости на
горизонтальной проекции и малую ось эллипса 2-2.
Аналогично построим горизонтальную проекцию эллипса с
большой осью CD.
Содержание
61.
9. ПЛОСКОСТЬ, КАСАТЕЛЬНАЯ К ПОВЕРХНОСТИ, НОРМАЛЬ ПОВЕРХНОСТИ9.1 а*. В точке А построить касательную плоскость и нормаль
поверхности.
Построим горизонтальную проекцию А’ точки А с помощью
образующей S1.
Проекции касательной плоскости.
Заданный конус имеет в горизонтальных плоскостях сечения –
окружности. Построим проекции такой окружности m (m ‘, m”) через
точку A.
Прямая t1 (t1‘, t1”) касательной плоскости касается окружности в точке А.
Вторая прямая t2 (t2‘, t2”) касательной плоскости является образующей
конуса, проходящей через точку А (t2 ≡ S1).
Проекции нормали.
Прямая t1 – горизонталь касательной плоскости, поэтому
горизонтальная проекция нормали n‘ ⊥ t1‘ .
Фронтальная проекция нормали n” должна быть перпендикулярна
фронтальной проекции фронтали касательной плоскости.
Построим произвольную фронталь касательной плоскости. Например,
фронтали S2.
Проекция нормали n‘‘⊥ S‘’2‘’.
Содержание
62.
9.3*. В точке А построить касательную плоскость и нормаль поверхности тора.Проекции касательной плоскости. Построим фронтальную проекцию А”
точки А, используя параллель (окружность m) тора.
Через точку А построим проекцию второй окружности l кругового сечения
тора, проходящего через ось тора. Отметим, что на фронтальную
плоскость π2 окружность m проецируется в прямую m”, а окружность l –
в эллипс l ” .
Построим касательные tm и tl к этим окружностям в точке А.
Горизонтальные проекции прямых tm’ и tl’, соответственно касательные к
окружностям m и l в точке А, образуют горизонтальную проекцию
касательной плоскости.
Для упрощения построений фронтальной проекции касательной плоскости
воспользуемся вращением вокруг проецирующей прямой – оси тора.
Переместим окружность l в положение, параллельное плоскости π2
lo (lo ’, lo “ ). В этом положении построим проекции прямой to , касательной
к окружности lo .
Фронтальную проекцию касательной tl“ построим, используя вершину Sk
конуса касательных.
Проекции нормали. Прямая tm является горизонтальной касательной
плоскости, поэтому горизонтальная проекция нормали n‘ ⊥ tm‘ и n’ ≡ tl
’.
Фронтальную проекцию нормали n” построим, используя вершину Sn
Содержание
63.
10. РАЗВЕРТКА ПОВЕРХНОСТЕЙ10.2*. Построить развертку призмы с использованием нормальных сечений.
Развертку призмы можно выполнить, используя нормальное сечение (сечение перпендикулярное боковым ребрам и
граням призмы).
Боковые ребра призмы
расположены параллельно
плоскости проекций π2.
Задаем плоскость нормального
сечения γ ⊥ π2 .
Истинный вид нормального сечения
получим, используя способ замены
плоскостей проекций.
На горизонтальной прямой
«разложим» действительные
величины сторон треугольника
сечения 1-2-3
На вертикальных прямых отложим
величины ребер, используя их
фронтальные проекции.
Соединим конечные точки.
Построим треугольники оснований.
Содержание
64.
10.3*. Построить условную развертку полусферы с использованием цилиндрических поверхностей.Построим условную развертку сферы, используя аппроксимацию сферы отсеками цилиндрических поверхностей.
Пересечем сферу горизонтально проецирующими плоскостями, проходящими через центр сферы. Сфера таким
образом может быть «разрезана» на 6, 8, 12 равных частей.
Каждую часть сферы заменим отсеком цилиндрической поверхности, касательной к экватору сферы и
перпендикулярной фронтальной плоскости проекций. Фронтальная проекция цилиндрической поверхности
совпадает с главным меридианом сферы.
Развернем участок цилиндрической поверхности, заменяя дуги окружности цилиндрической поверхности хордами и
откладывая соответствующие образующие цилиндра.
Содержание
65.
11. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ11.1*. Достроить горизонтальную проекцию пирамиды и построить ее изометрическую проекцию.
Достроим горизонтальную
проекцию пирамиды (треугольник
сечения 1-2-3).
Построим проекцию высоты
пирамиды и точки S.
Используя координаты x и y ,
построим аксонометрическую
проекцию основания АВС.
Аксонометрическую проекцию
треугольника сечения строим,
используя координаты x и y точек
1, 2, 3.
Через полученные вторичные
проекции точек 1, 2, 3 проводим
прямые, параллельные оси z до
пересечения с соответствующими
ребрами пирамиды. Соединяем
проекции точек 1, 2, 3.
Содержание









































 drafting
drafting








