Similar presentations:
Пересечение поверхностей плоскостями
1. Пересечение поверхностей плоскостями
2.
• Определить сечение прямой призмыплоскостью общего положения и истинную
величину этого сечения
3.
Ребра прямой призмыперпендикулярны
горизонтальной
плоскости и проектируются в
точки. В эти же точки
проецируются
и вершины сечения ABC.
Обозначим горизонтальные
проекции этих вершин
4.
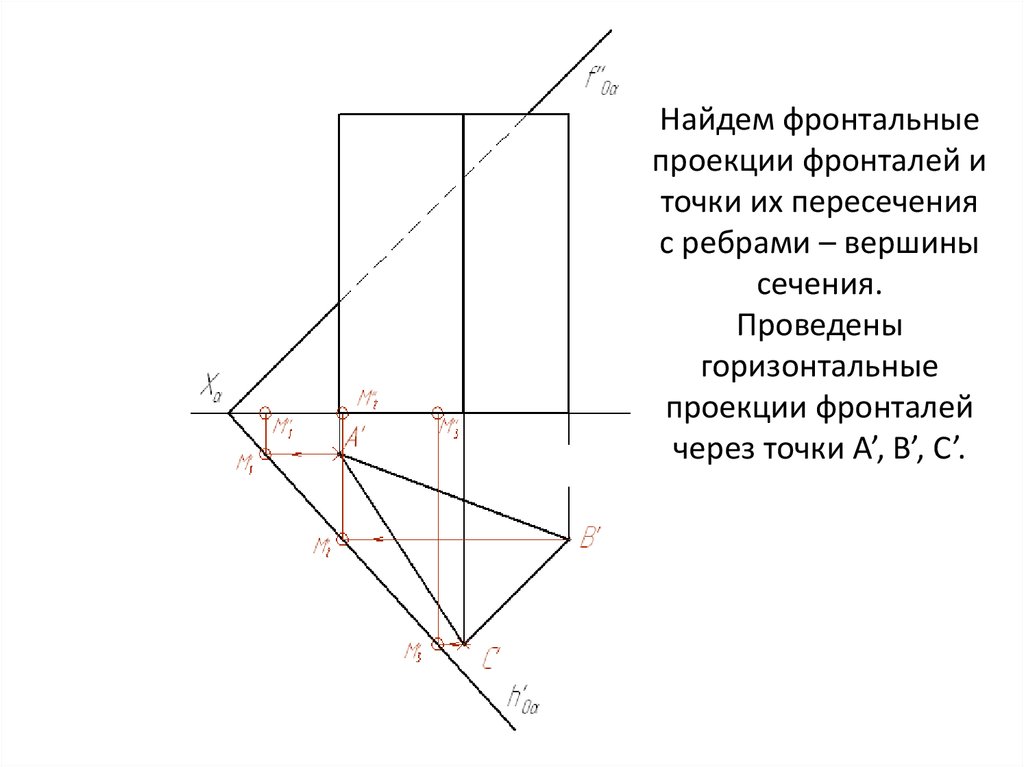
Найдем фронтальныепроекции фронталей и
точки их пересечения
с ребрами – вершины
сечения.
Проведены
горизонтальные
проекции фронталей
через точки A’, B’, C’.
5.
A’’,B’’,C’’ - фронтальные проекциивершин сечения в точках пересечения
ФПФ с соответствующими ребрами
пирамиды.
Истинную величину сечения
найдем вращением его вокруг
горизонтали h’0α (следа плоскости
сечения). При этом вся
плоскость α совмещается с пл. π1,
равно как и все элементы,
заключенные в этой плоскости.
На следе f’’0α выделим точку
N(N’’,N’’), и построим фронтальные
проекции горизонталей
через вершины многоугольника
сечения, а также проекции их
фронтальных следов (N’’3 , N’’1 , N’’2 ).
6.
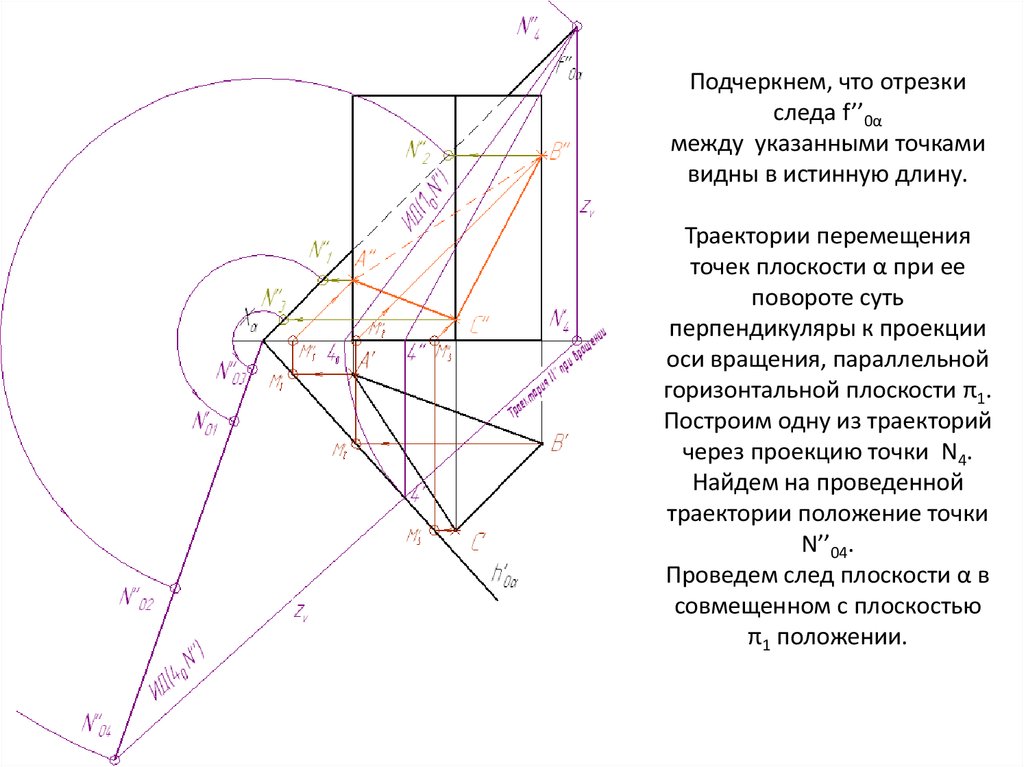
Подчеркнем, что отрезкиследа f’’0α
между указанными точками
видны в истинную длину.
Траектории перемещения
точек плоскости α при ее
повороте суть
перпендикуляры к проекции
оси вращения, параллельной
горизонтальной плоскости π1.
Построим одну из траекторий
через проекцию точки N4.
Найдем на проведенной
траектории положение точки
N’’04.
Проведем след плоскости α в
совмещенном с плоскостью
π1 положении.
7.
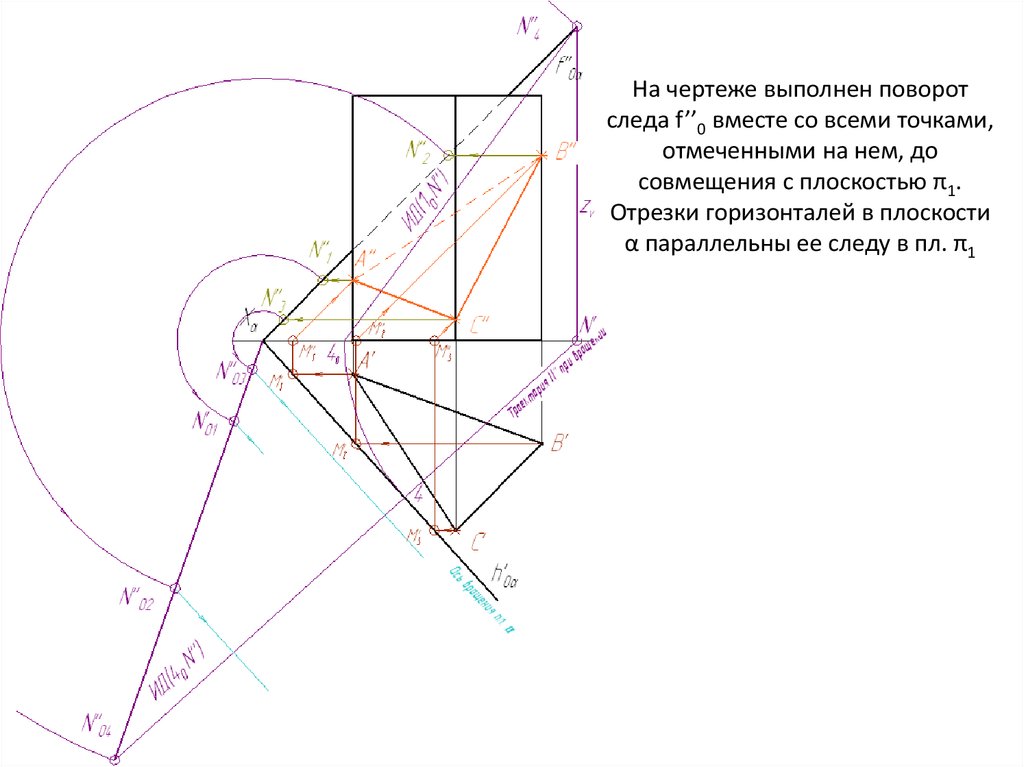
На чертеже выполнен поворотследа f’’0 вместе со всеми точками,
отмеченными на нем, до
совмещения с плоскостью π1.
Отрезки горизонталей в плоскости
α параллельны ее следу в пл. π1
8.
Построены фронтальныепроекции горизонталей в
совмещенной с плоскостью π1
положении.
Построены траектории
горизонтальных проекций
вершин сечения призмы и
определено их положение в
совмещенной плоскости.
С использованием точки 4
пересечения траектории точки
с горизонтальным следом
плоскости h’0α , показана
альтернативная возможность
определения истинной длины
отрезка «4N’’» - 40 N’’4
9.
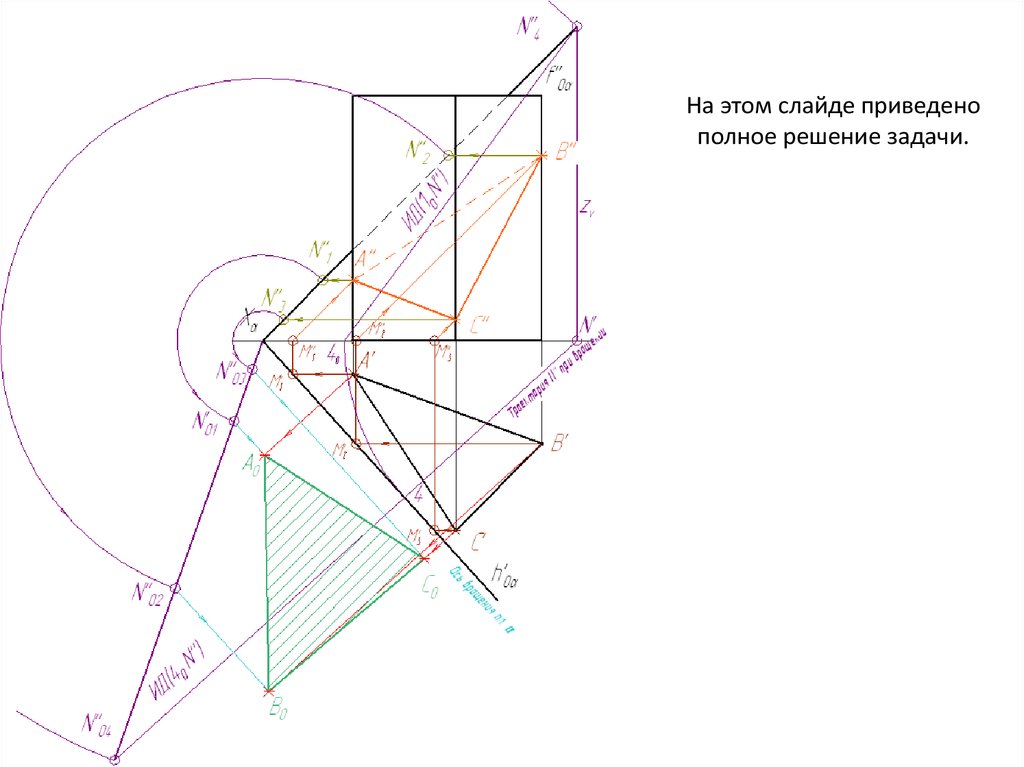
На этом слайде приведенополное решение задачи.
10.
• Пересечение правильной пирамидыпроецирующей плоскостью
Основание пирамиды заключено в горизонтальную плоскость.
Секущая плоскость проецирует на фронтальную плоскость
проекций. На этой плоскости фронтальная проекция сечения
располагается на фронтальном следе заданной плоскости
11.
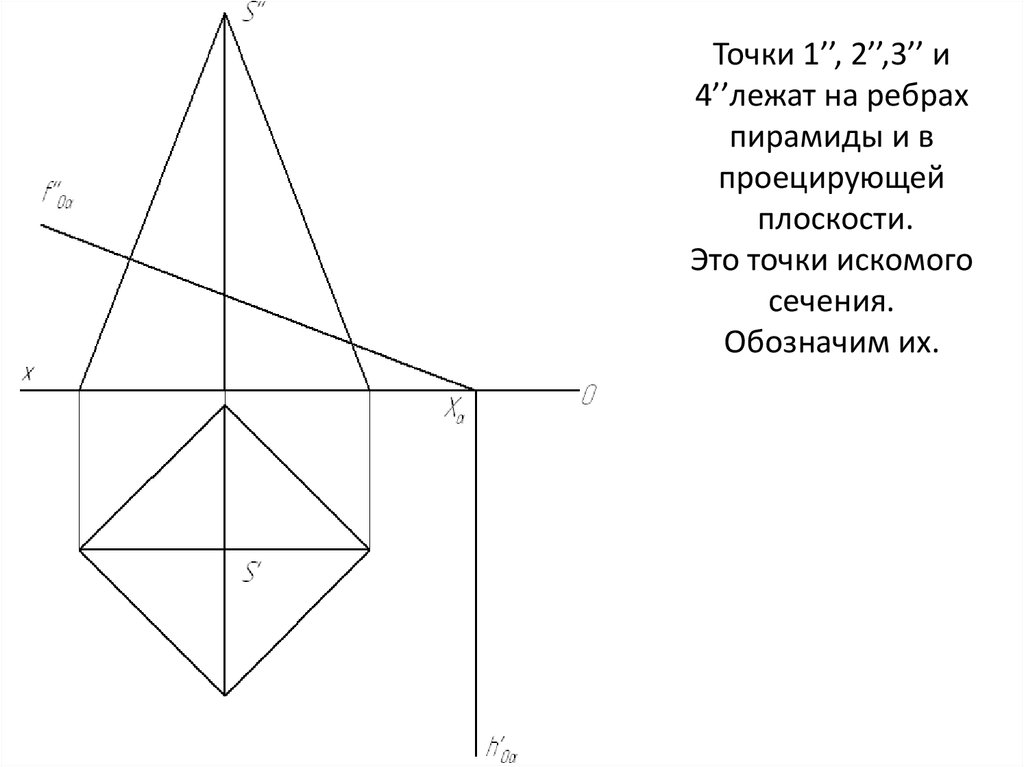
Точки 1’’, 2’’,3’’ и4’’лежат на ребрах
пирамиды и в
проецирующей
плоскости.
Это точки искомого
сечения.
Обозначим их.
12.
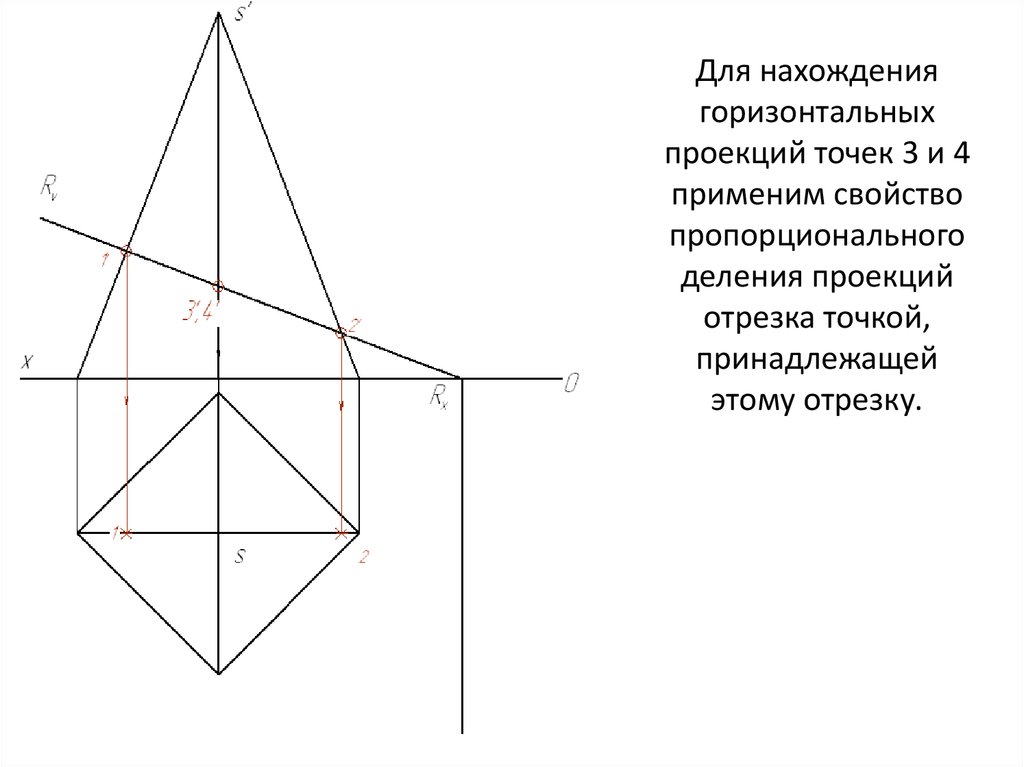
Для нахождениягоризонтальных
проекций точек 3 и 4
применим свойство
пропорционального
деления проекций
отрезка точкой,
принадлежащей
этому отрезку.
13.
Отрезок 3’’5’’ делитребро S5 том же
отношении, в котором
точки 3’ и 4’ делят ребра
S3 и S4.
Используя это свойство
проецирования, найдем
горизонтальные
проекции точек сечения.
В каждой грани
пирамиды имеем по
две точки,
определяющие
отрезки ломаной
линии контура
сечения.
14.
Истинную величину сечениянайдем методом его вращения
вокруг фронтали, в качестве
которой выберем фронтальный
след плоскости α.
Траектории перемещения точек
сечения и горизонтальных следов
фронталей, проведенных через
горизонтальные проекции этих
точек, есть перпендикуляры
к фронтальному следу плоскости.
15.
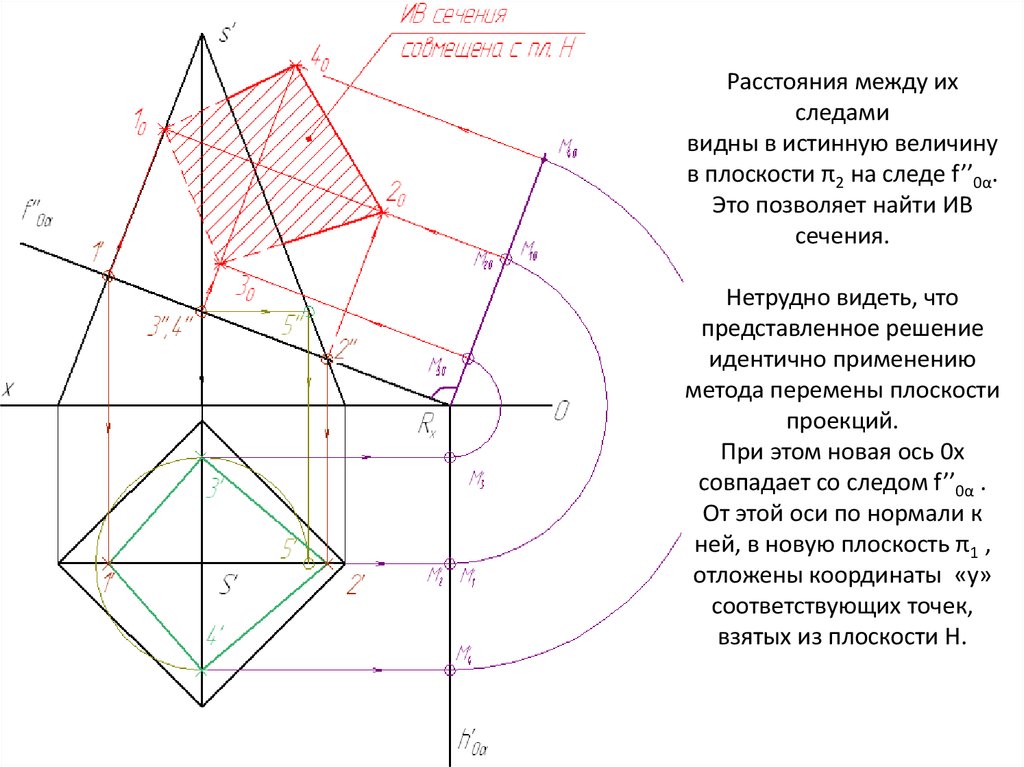
Расстояния между ихследами
видны в истинную величину
в плоскости π2 на следе f’’0α.
Это позволяет найти ИВ
сечения.
Нетрудно видеть, что
представленное решение
идентично применению
метода перемены плоскости
проекций.
При этом новая ось 0x
совпадает со следом f’’0α .
От этой оси по нормали к
ней, в новую плоскость π1 ,
отложены координаты «y»
соответствующих точек,
взятых из плоскости H.
16.
• Построить сечение наклонного цилиндрагоризонтально проецирующей плоскостью
17.
Найдем наивысшуюточку искомого
сечения (ВТС),
лежащую
на образующей
поверхности
цилиндра. След этой
образующей
удален от
горизонтального
следа проецирующей
плоскости на
наибольшее
расстояние.
18.
На горизонтальнойпроекции линии
пересечения
обозначим
проекции точек
на пл.π1
19.
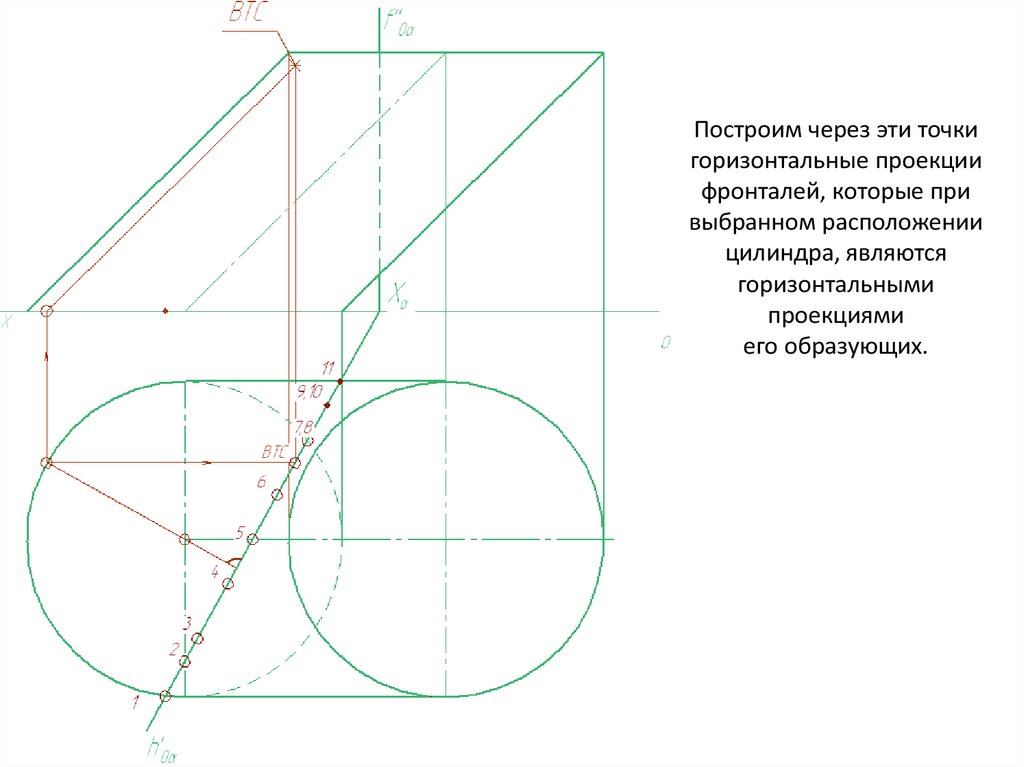
Построим через эти точкигоризонтальные проекции
фронталей, которые при
выбранном расположении
цилиндра, являются
горизонтальными
проекциями
его образующих.
20.
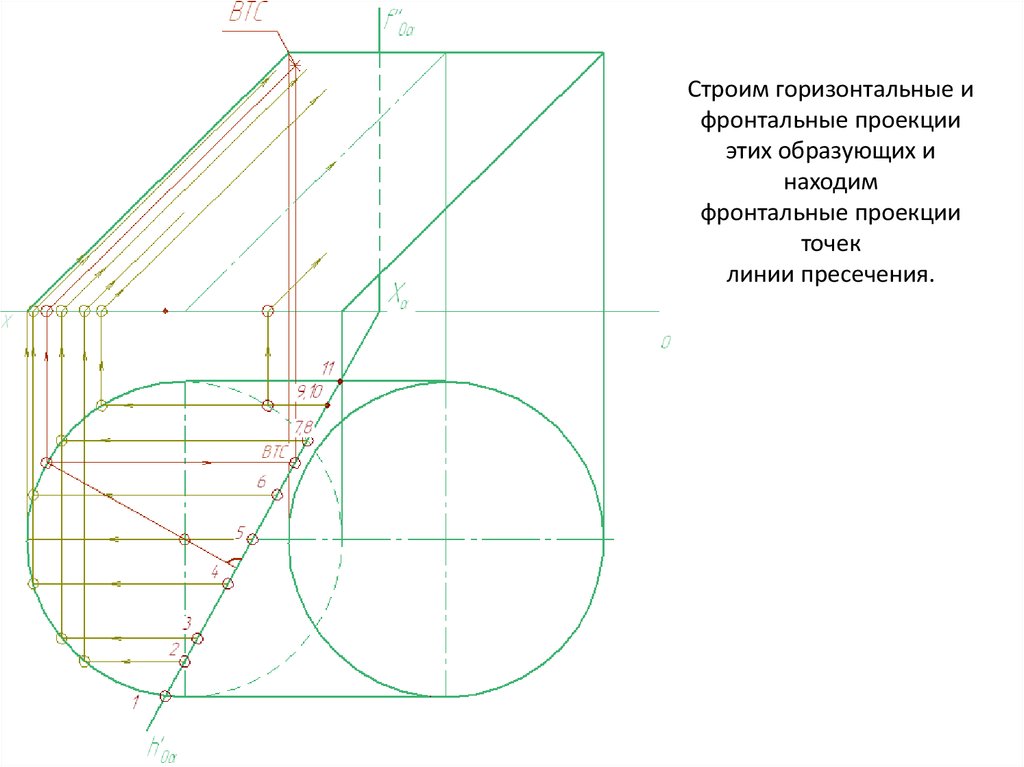
Строим горизонтальные ифронтальные проекции
этих образующих и
находим
фронтальные проекции
точек
линии пресечения.
21.
Строим фронтальнуюпроекцию линии
пересечения.
22.
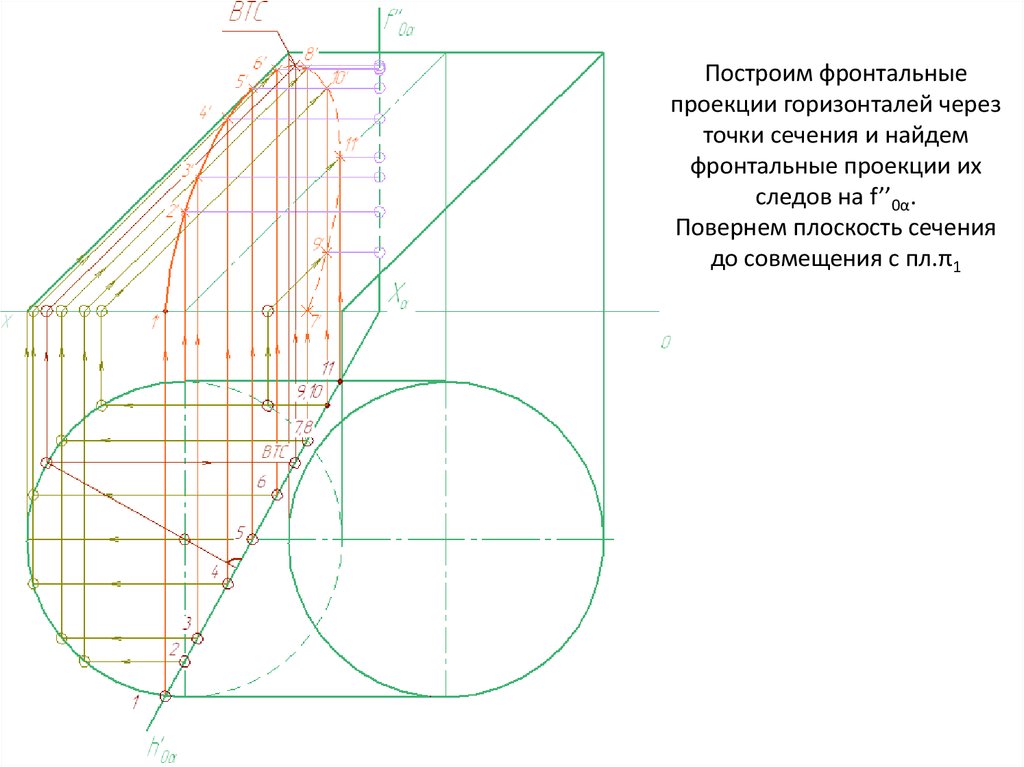
Построим фронтальныепроекции горизонталей через
точки сечения и найдем
фронтальные проекции их
следов на f’’0α.
Повернем плоскость сечения
до совмещения с пл.π1
23.
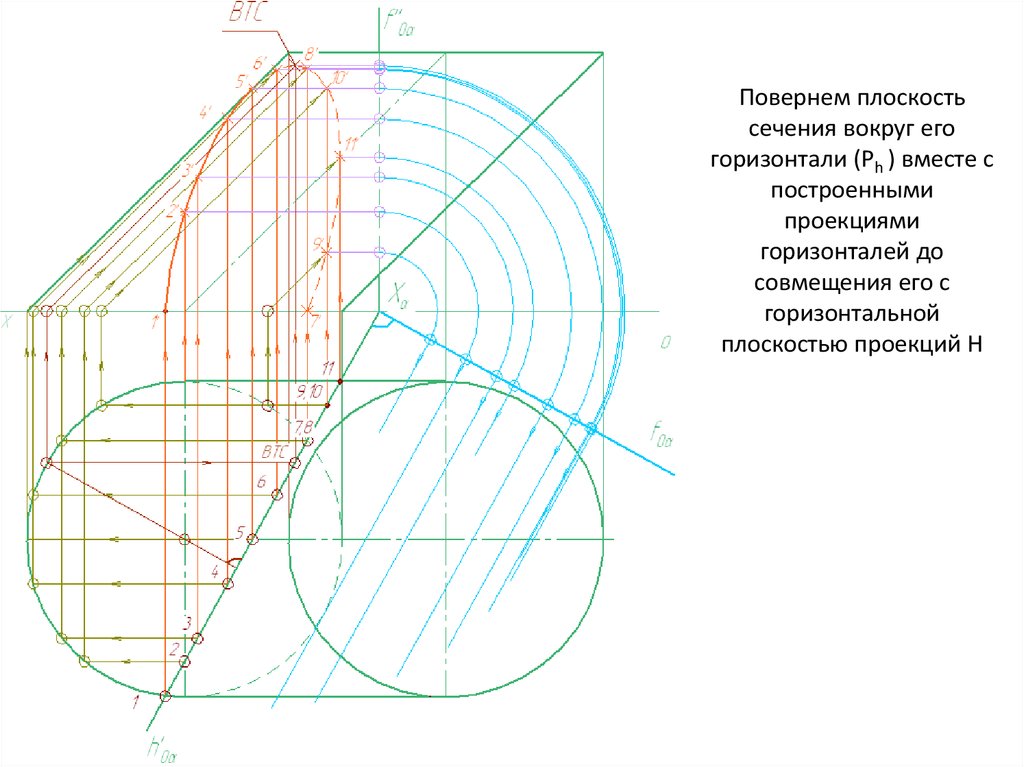
Повернем плоскостьсечения вокруг его
горизонтали (Ph ) вместе с
построенными
проекциями
горизонталей до
совмещения его с
горизонтальной
плоскостью проекций H
24.
Траектории обозначенныхточек сечения в
горизонтальной
плоскости проекций суть
перпендикуляры к следу
пл.π1.
Находим точки пересечения
траекторий с
соответствующими
горизонталями и
строим истинную
величину сечения.
25.
• Сечение наклонного конуса горизонтальнопроецирующей плоскостью
Наклонный конус основанием опирается на пл.π1
26.
Найдем наивысшую точкуискомого сечения (ВТС),
лежащую
на образующей поверхности
конуса. След этой образующей
удален от горизонтального
следа проецирующей
плоскости на наибольшее
расстояние.
27.
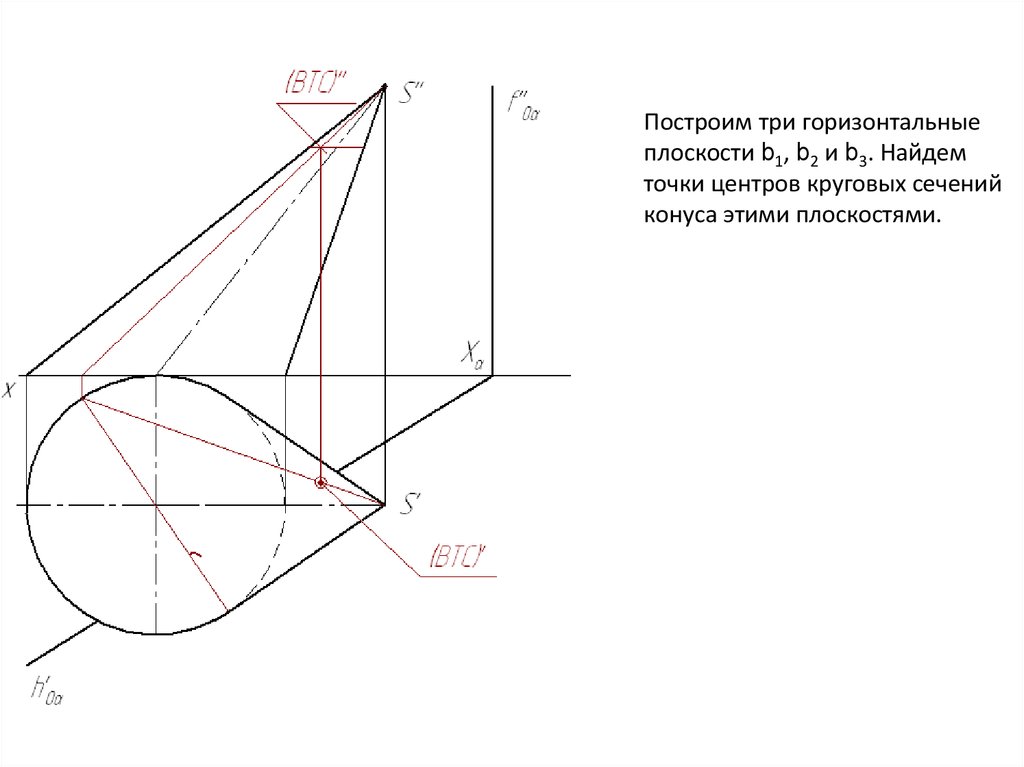
Построим три горизонтальныеплоскости b1, b2 и b3. Найдем
точки центров круговых сечений
конуса этими плоскостями.
28.
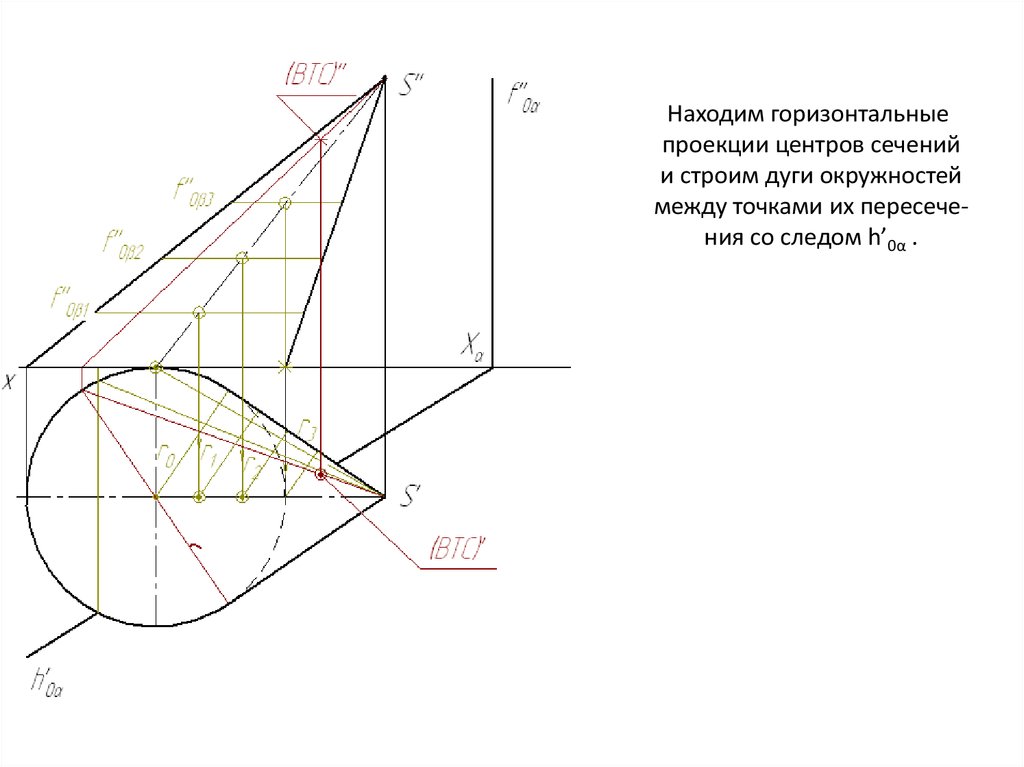
Находим горизонтальныепроекции центров сечений
и строим дуги окружностей
между точками их пересечения со следом h’0α .
29.
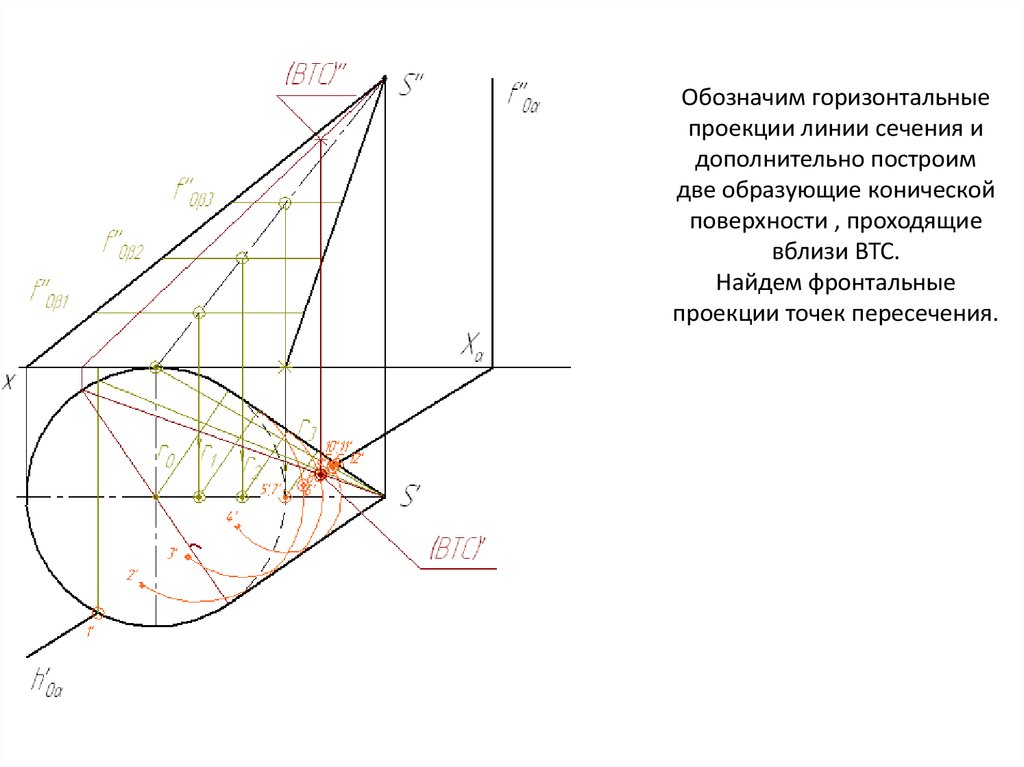
Обозначим горизонтальныепроекции линии сечения и
дополнительно построим
две образующие конической
поверхности , проходящие
вблизи ВТС.
Найдем фронтальные
проекции точек пересечения.
30.
Обозначим фронтальныепроекции точек сечения и
построим контур сечения
во фронтальной плоскости
31.
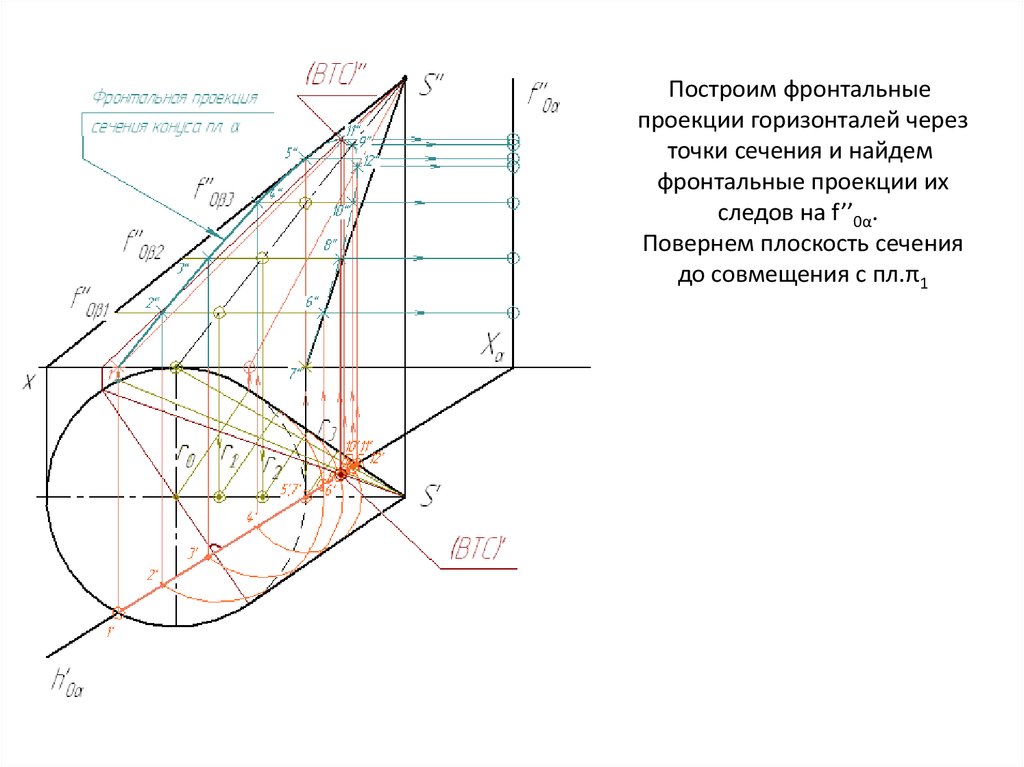
Построим фронтальныепроекции горизонталей через
точки сечения и найдем
фронтальные проекции их
следов на f’’0α.
Повернем плоскость сечения
до совмещения с пл.π1
32.
Повернем плоскостьсечения вокруг его
горизонтали (f’0α ) вместе с
построенными
проекциями горизонталей
до совмещения её с
горизонтальной
плоскостью проекций π1
33.
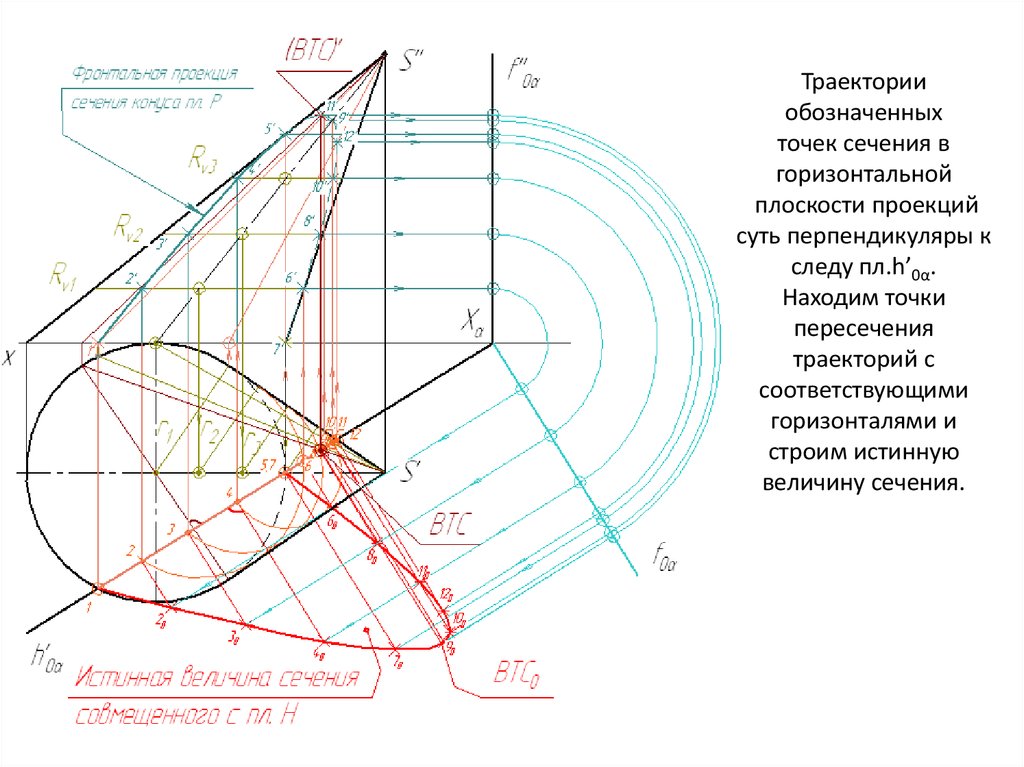
Траекторииобозначенных
точек сечения в
горизонтальной
плоскости проекций
суть перпендикуляры к
следу пл.h’0α.
Находим точки
пересечения
траекторий с
соответствующими
горизонталями и
строим истинную
величину сечения.

















 drafting
drafting








