Similar presentations:
Рабочая тетрадь для практических занятий по начертательной геометрии
1.
МГТУ им.Н.Э. Баумана
Рабочая тетрадь
для практических занятий по начертательной геометрии
Задачи для самостоятельной работы студентов
Авторы: доценты, к.т.н. Сенченкова Л.С., к.т.н. Палий Н.В., ст. пр. Белобородова Т.Л.
под редакцией доцента, к.т.н. Боровикова И.Ф.
2.
СОДЕРЖАНИЕПРОЕКЦИИ ТОЧКИ ▼
ЗАДАНИЕ ПРЯМОЙ ЛИНИИ НА ЧЕРТЕЖЕ ▼
ЗАДАНИЕ ПЛОСКОСТИ НА ЧЕРТЕЖЕ. ТОЧКА И ПРЯМАЯ В ПЛОСКОСТИ ▼
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ ▼
ПРОЕКЦИИ МНОГОГРАННИКОВ ▼
СПОСОБЫ ПРЕОБРАЗОВАНИЯ. МЕТРИЧЕСКИЕ ЗАДАЧИ ▼
Способ замены плоскостей проекций ▼
Способ плоскопараллельного перемещения ▼
Способ вращения вокруг проецирующей прямой ▼
Композиция преобразований ▼
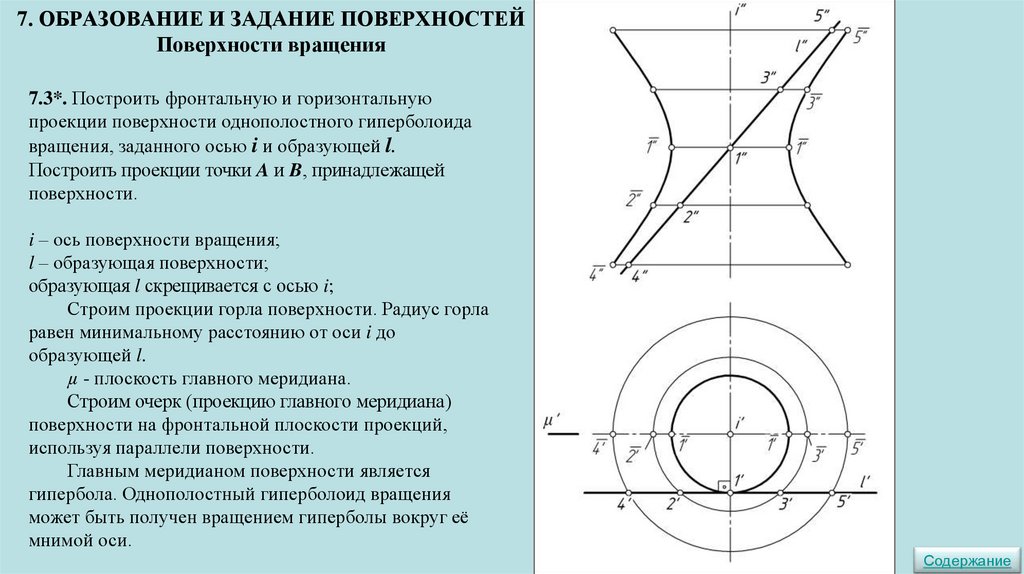
7. ОБРАЗОВАНИЕ И ЗАДАНИЕ ПОВЕРХНОСТЕЙ ▼
Поверхности вращения ▼
Винтовая поверхность ▼
1.
2.
3.
4.
5.
6.
Для в перехода к нужному разделу требуется нажать знак ▼
3.
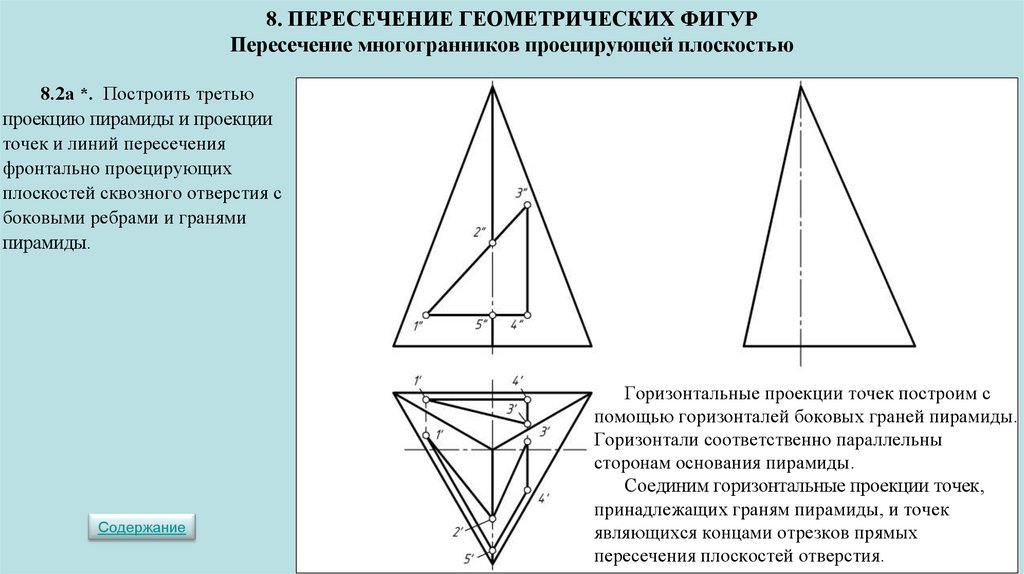
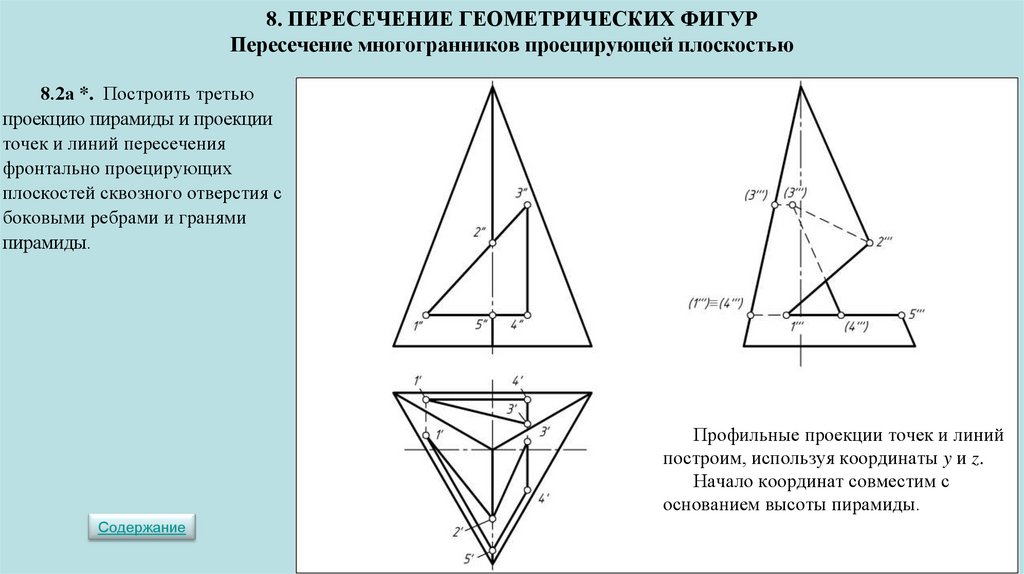
СОДЕРЖАНИЕ8. ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР ▼
Пересечение многогранников проецирующей плоскостью ▼
Пересечение тел вращения проецирующей плоскостью ▼
Пересечение прямой и плоскости, двух плоскостей ▼
Пересечение прямой линии и поверхности ▼
Пересечение поверхностей, одна из которых проецирующая ▼
Пересечение поверхностей с использованием вспомогательных проецирующих плоскостей ▼
Пересечение поверхностей. Частные случаи ▼
9. ПЛОСКОСТЬ, КАСАТЕЛЬНАЯ К ПОВЕРХНОСТИ, НОРМАЛЬ ПОВЕРХНОСТИ ▼
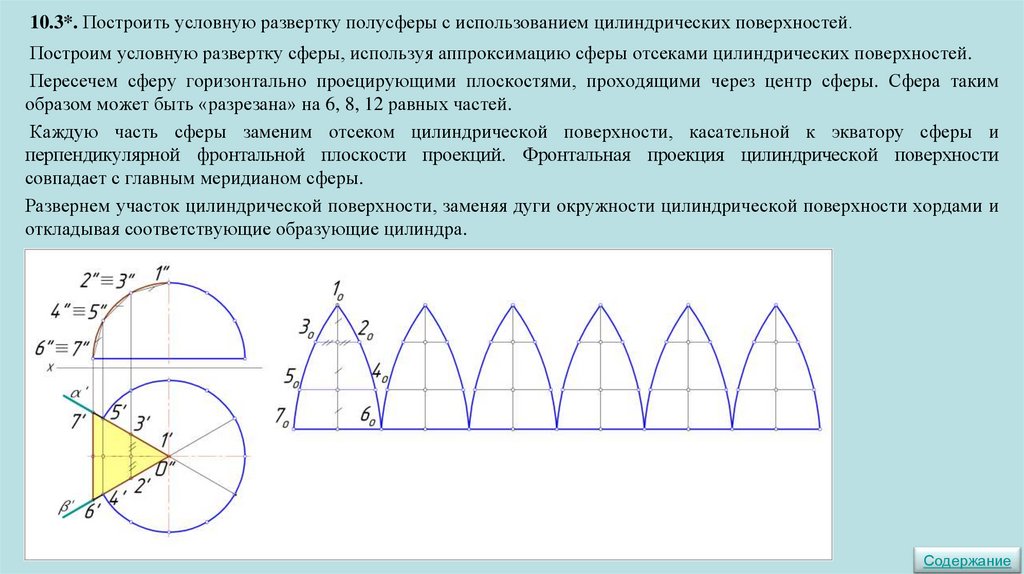
10. РАЗВЕРТКА ПОВЕРХНОСТЕЙ ▼
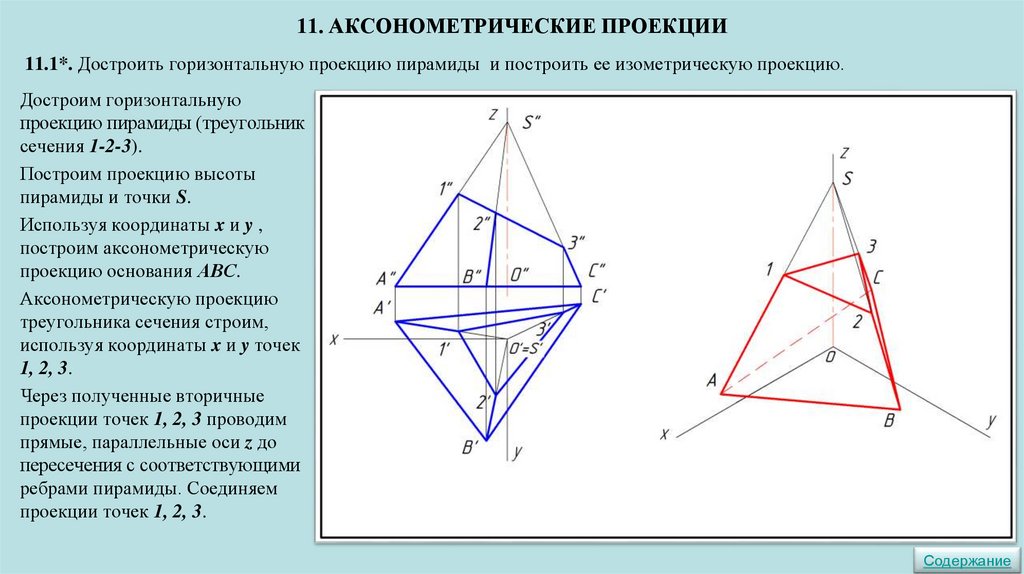
11. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ ▼
Для в перехода к нужному разделу требуется нажать знак ▼
4.
1. ПРОЕКЦИИ ТОЧКИПроекции точки на две плоскости проекций
Расстояние от точки до
горизонтальной плоскости
проекций 1 определяет
координата z.
На чертеже значение
координаты z равно
расстоянию от оси проекций
Оx до фронтальной проекции
точки Aʺ .
Расстояние от точки до
фронтальной плоскости
проекций 2 определяет
координата y.
На чертеже значение
координаты y равно
расстоянию от оси проекций
Оx до горизонтальной
проекции точки A′ .
Содержание
5.
Проекции точки на три плоскости проекцийРасстояние от точки до
профильной плоскости
проекций 3 определяет
координата х.
На чертеже значение
координаты х равно расстоянию
от оси проекций Оz до
фронтальной проекции точки
или от оси проекций Оy до
горизонтальной проекции
точки.
Горизонтальная проекция A′
точки A определяется
координатами х, y.
Фронтальная проекция Aʺ
точки A определяется
координатами х, z.
Профильная проекция A′′′
точки A определяется
координатами y, z.
Содержание
6.
1.8*. Построить проекции точки A, лежащей в плоскости проекций 2 иудаленной от плоскости 1 на расстояние 30 мм, от 3 – на 40 мм.
Горизонтальная проекция A′ точки A
определяется координатами x, y;
Фронтальная проекция Aʺ точки A
определяется координатами x, z;
Профильная проекция A′′′ точки A
определяется координатами у, z.
Расстояние от точки до профильной
плоскости проекций 3 определяет
координата х (xA = 40).
Расстояние от точки до горизонтальной
плоскости проекций 1 определяет
координата z (zA = 30).
Если точка А 2 , то yA = 0
Для решения задачи воспользуемся
последовательно значениями координат:
xA = 40; yA = 0; zA = 30.
Содержание
7.
1.9*. Построить проекции точки A, лежащей на оси проекций Oх иудаленной от плоскости проекций 3 на расстояние 40 мм.
Расстояние от точки до профильной
плоскости проекций 3 определяет
координата х (xA = 40);
Если точка А Ох, то yA = 0, zA = 0.
Для решения задачи воспользуемся
последовательно значениями
координат:
A′ (x, y); Aʺ (x, z); A′′′ (у, z),
а именно:
A′ (40, 0); Aʺ (40, 0); A′′′ (0, 0).
Содержание
8.
1.10*. Построить проекции точки В, которая относительно точки Aрасположена на 15 мм дальше от плоскости проекций 1 , на 20 мм
ближе к 2 и на 10 мм дальше от 3 .
Построение с использованием разности
координат можно начинать в следующем
порядке:
– определяем горизонтальную проекцию
точки В′ (xВ ; yВ ):
xВ > xA на 10 мм; xВ = xA + 10 мм;
yВ < yA на 20 мм; yВ = yA – 20 мм;
– определяем фронтальную проекцию
точки Вʺ(xВ ; zВ ):
zВ > zA на 15 мм; zВ = zA + 15 мм.
Профильная
проекция
точки
В′′′
определяется координатами yВ ; zВ .
Содержание
9.
1.11*. Построить горизонтальную и профильную проекции точки A,удаленной от оси проекций Oх на расстояние 35 мм.
Ось Ох 3 и проецируется на
плоскость 3 в точку начала
координат О.
Множество точек на плоскости
3 с расстоянием 35 мм от начала
координат
О
образуют
окружность радиусом 35 мм с
центром в начале координат.
Воспользуемся линиями связи и
координатами yA и zA , строим
проекции точки А .
Содержание
10.
2. ЗАДАНИЕ ПРЯМОЙ ЛИНИИ НА ЧЕРТЕЖЕ2.2. д* Построить проекции отрезка MN. Отрезок MN равен 15 мм и перпендикулярен фронтальной
плоскости проекций
Используя проекции М′ и М′′′ с
помощью линий связи строим
фронтальную проекцию Мʺ конца
отрезка.
Так как отрезок MN 2 , то на
плоскость 2 он проецируется в точку
Мʺ Nʺ.
Из условия, что отрезок MN 2 (MN 1)
и равен 15 мм, определяем положение
проекции N′( M′N′ =15 мм).
Профильную проекцию точки N′′′
строим, используя координату уN .
Соединяя одноименные проекции точек
М и N, получим проекции отрезка МN.
Содержание
11.
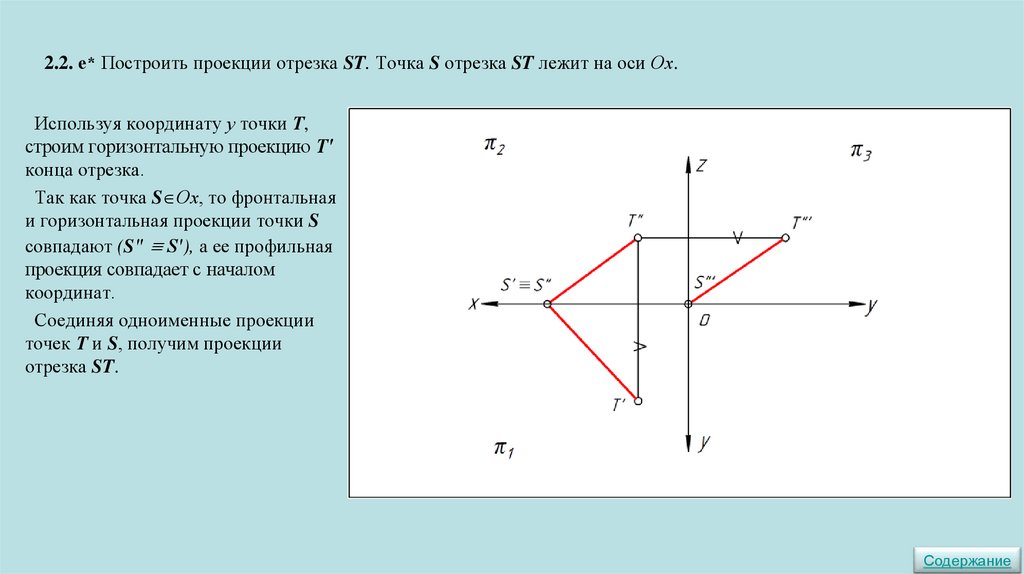
2.2. е* Построить проекции отрезка ST. Точка S отрезка ST лежит на оси Ох.Используя координату у точки Т,
строим горизонтальную проекцию Т′
конца отрезка.
Так как точка S Ох, то фронтальная
и горизонтальная проекции точки S
совпадают (Sʺ S′), а ее профильная
проекция совпадает с началом
координат.
Соединяя одноименные проекции
точек Т и S, получим проекции
отрезка ST.
Содержание
12.
2.6*. Построить проекции прямой d, параллельной прямой а ипересекающей прямые b и с.
Обозначим искомые точки пересечения
прямой d с прямыми b и с:
d c M; d b K .
Так как M d и M c, то M’’ c’’ (c 2
и проецируется в точку на 2 )
D’’ a’’– строим фронтальную
проекцию прямой d ’’ ;
d b K;
Так как К d , К b, то через К’
строим проекцию d’ (d’ a’ ) M’.
При решении используем свойство
параллельности прямых.
Содержание
13.
2.8*. Построить проекции прямой с, пересекающей прямые а и b подпрямым углом.
Так как прямая a 1 , то
перпендикулярная к ней прямая с 1 ,
т.е. горизонтальная прямая. По теореме
о проекциях прямого угла угол между
горизонтальными проекциями с′ и b′ –
прямой.
Фронтальная проекция прямой
сʺ оси Ох, т.к. прямая с – горизонталь
(с a M; с b K).
Содержание
14.
2.9*. Построить проекции отрезка BD, перпендикулярного отрезку AC, если точка пересечения этих отрезковделит их пополам, точка B принадлежит фронтальной плоскости проекций, а точка D равноудалена от
плоскостей проекций.
AC – горизонтальная прямая;
BD AC; BD AC K; AK=KC.
Так как точка B 2 , то ее
горизонтальная
проекция
B’ Ох
(координата yB = 0); BK=KD.
Проекцию точки Dʺ строим из условия,
что yD = zD (равное удаление от 1 и 2 ).
Используя линию связи строим
проекцию Bʺ.
Содержание
15.
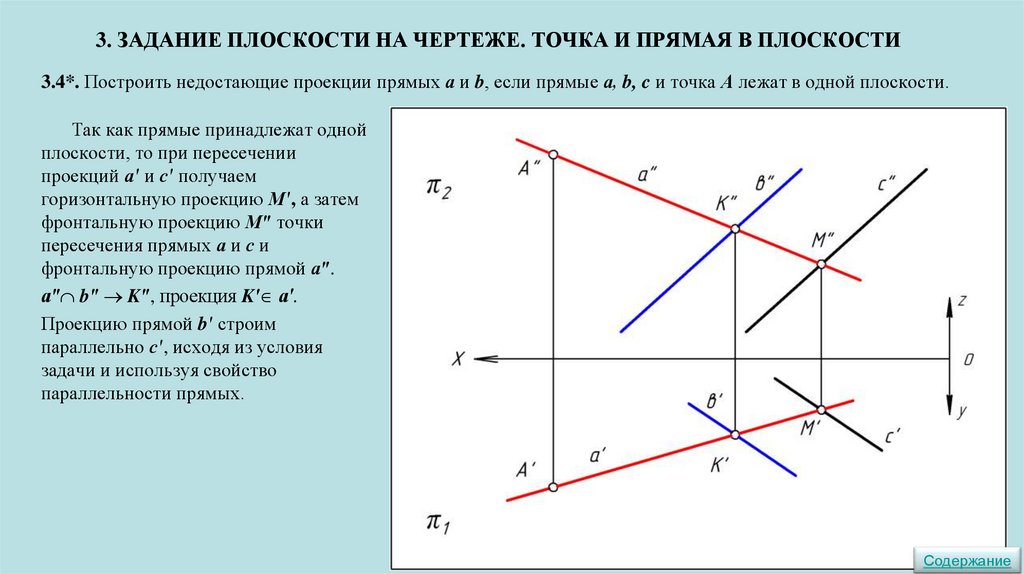
3. ЗАДАНИЕ ПЛОСКОСТИ НА ЧЕРТЕЖЕ. ТОЧКА И ПРЯМАЯ В ПЛОСКОСТИ3.4*. Построить недостающие проекции прямых а и b, если прямые а, b, c и точка А лежат в одной плоскости.
Так как прямые принадлежат одной
плоскости, то при пересечении
проекций а′ и с′ получаем
горизонтальную проекцию М′, а затем
фронтальную проекцию Мʺ точки
пересечения прямых а и с и
фронтальную проекцию прямой аʺ.
аʺ bʺ Kʺ, проекция K′ а′.
Проекцию прямой b′ строим
параллельно с′, исходя из условия
задачи и используя свойство
параллельности прямых.
Содержание
16.
4. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ4.2*. Достроить горизонтальную проекцию треугольника АВС, плоскость которого параллельна прямой а.
На основании признака
параллельности прямой и плоскости
построим в плоскости, заданной
треугольником АВС, прямую d a .
Начнем с фронтальной проекции dʺ,
далее M АС; В d .
Содержание
17.
4.7*. Построить горизонтальную проекцию прямой b, пересекающейпрямую а в точке К, если прямые a и b взаимно перпендикулярны.
Множество прямых, пересекающих в
точке заданную прямую и
перпендикулярных к ней, образуют
плоскость , перпендикулярную заданной
прямой.
Задаем плоскость с помощью
горизонтали h и фронтали f.
(h f ) ; h a ; f a – основанием
является признак перпендикулярности
прямой и плоскости и теорема о проекциях
прямого угла.
Прямая b принадлежит плоскости ,
проходящей через точку K и
перпендикулярной прямой а.
С помощью произвольной прямой с,
принадлежащей плоскости , построим
проекции точки М и прямой b.
М ; М b ; М′ b′.
Содержание
18.
4.8*. Достроить фронтальную проекцию треугольника АВС, плоскостькоторого перпендикулярна к заданной плоскости α(a, b).
На основании признака перпендикулярности
прямой и плоскости и теоремы о проекциях прямого
угла построим проекции перпендикуляра n к
плоскости α(a, b) через точку B, принадлежащую
плоскости
ABC.
Чтобы плоскости были взаимно
перпендикулярны, прямая n должна принадлежать
плоскости ABC (признак перпендикулярности двух
плоскостей).
Достроим фронтальную проекцию ABC,
используя проекции точки 1 (1 n, 1 АС).
Содержание
19.
5. ПРОЕКЦИИ МНОГОГРАННИКОВДля решения представленных задач построения проекций многогранников сначала надо
определить расположение плоскостей граней и оснований и положение ребер относительно
плоскостей проекций.
Затем задача сводится к построению проекций отрезков прямых, которые являются либо
боковыми ребрами, либо сторонами оснований многогранников.
Содержание
20.
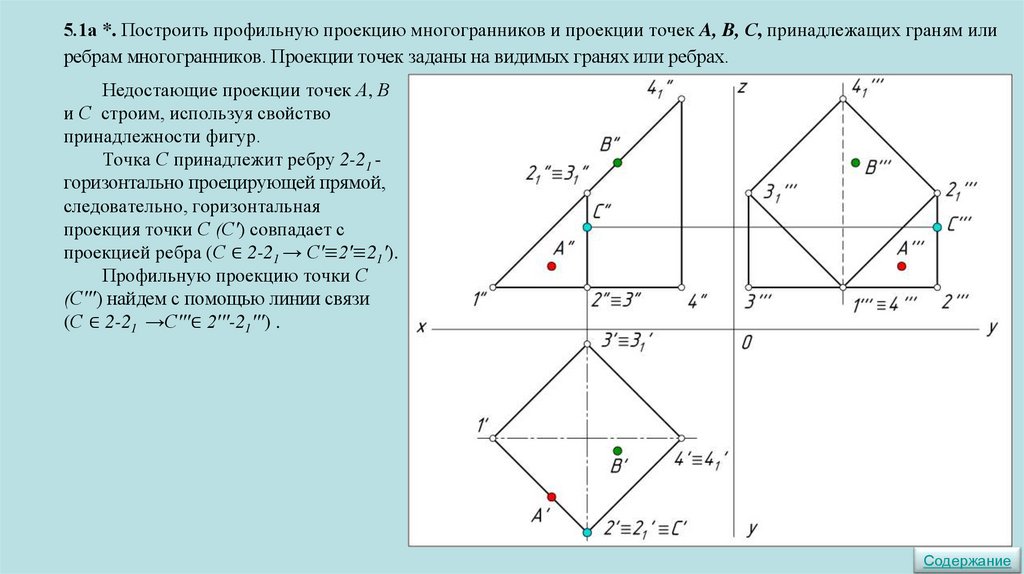
5.1а *. Построить профильную проекцию многогранников и проекции точек A, B, С, принадлежащих граням илиребрам многогранников. Проекции точек заданы на видимых гранях или ребрах.
Верхняя часть прямой
четырёхугольной призмы срезана
фронтально проецирующей плоскостью.
Нижнее основание призмы
параллельно π1, и следовательно
перпендикулярно π2 и π3.
Боковые рёбра принадлежат
горизонтально проецирующим прямым,
следовательно, параллельны плоскостям
π2 и π3.
Боковые грани перпендикулярны π1.
Для построения профильной
проекции используем координаты y и z.
Содержание
21.
5.1а *. Построить профильную проекцию многогранников и проекции точек A, B, С, принадлежащих граням илиребрам многогранников. Проекции точек заданы на видимых гранях или ребрах.
Недостающие проекции точек А, В
и С строим, используя свойство
принадлежности фигур.
Точка А принадлежит боковой
грани призмы 1-2-21 - горизонтально
проецирующей плоскости,
следовательно, горизонтальную
проекцию точки А (А′) найдем с
помощью линии связи
(А ∈ 1-2-21 →А′∈ 1′ -2′ -21′).
Профильную проекцию точки А
(А′′′) найдем с помощью координаты yА.
Точка В принадлежит фронтально
проецирующей плоскости 1-21 -31 -41 ,
следовательно, фронтальную проекцию
точки В (В′′) найдем с помощью линии
связи
(В ∈ 1-21 -31 -41 →В′′∈ 1′′-21 ′′-31 ′′-41 ′′).
Профильную проекцию точки В
(В′′′) найдем с помощью координаты yВ.
Содержание
22.
5.1а *. Построить профильную проекцию многогранников и проекции точек A, B, С, принадлежащих граням илиребрам многогранников. Проекции точек заданы на видимых гранях или ребрах.
Недостающие проекции точек А, В
и С строим, используя свойство
принадлежности фигур.
Точка С принадлежит ребру 2-21 горизонтально проецирующей прямой,
следовательно, горизонтальная
проекция точки С (С′) совпадает с
проекцией ребра (С ∈ 2-21 → С′≡2′≡21′).
Профильную проекцию точки С
(С′′′) найдем с помощью линии связи
(С ∈ 2-21 →С′′′∈ 2′′′-21′′′) .
Содержание
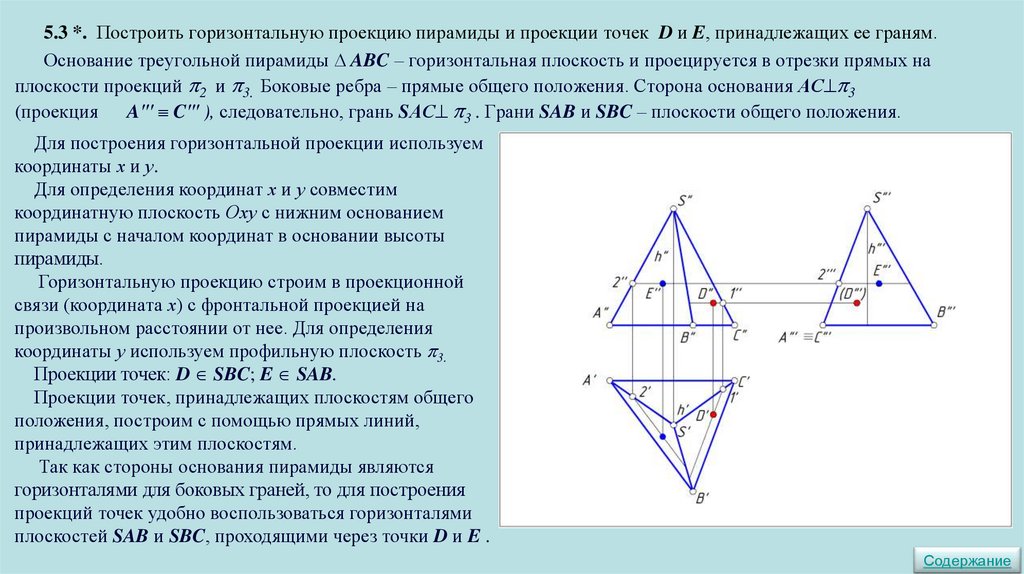
23.
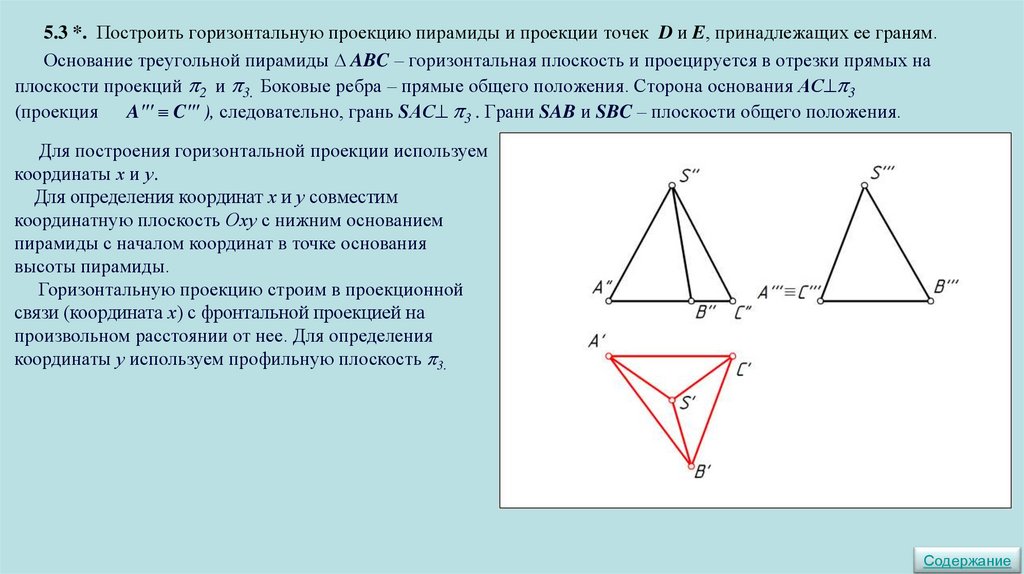
5.3 *. Построить горизонтальную проекцию пирамиды и проекции точек D и E, принадлежащих ее граням.Основание треугольной пирамиды ABC – горизонтальная плоскость и проецируется в отрезки прямых на
плоскости проекций 2 и 3. Боковые ребра – прямые общего положения. Сторона основания АС 3
(проекция A′′′ C′′′ ), следовательно, грань SАС 3 . Грани SAB и SBC – плоскости общего положения.
Для построения горизонтальной проекции используем
координаты х и у.
Для определения координат х и у совместим
координатную плоскость Оху с нижним основанием
пирамиды с началом координат в точке основания
высоты пирамиды.
Горизонтальную проекцию строим в проекционной
связи (координата х) с фронтальной проекцией на
произвольном расстоянии от нее. Для определения
координаты у используем профильную плоскость 3.
Содержание
24.
5.3 *. Построить горизонтальную проекцию пирамиды и проекции точек D и E, принадлежащих ее граням.Основание треугольной пирамиды ABC – горизонтальная плоскость и проецируется в отрезки прямых на
плоскости проекций 2 и 3. Боковые ребра – прямые общего положения. Сторона основания АС 3
(проекция A′′′ C′′′ ), следовательно, грань SАС 3 . Грани SAB и SBC – плоскости общего положения.
Для построения горизонтальной проекции используем
координаты х и у.
Для определения координат х и у совместим
координатную плоскость Оху с нижним основанием
пирамиды с началом координат в основании высоты
пирамиды.
Горизонтальную проекцию строим в проекционной
связи (координата х) с фронтальной проекцией на
произвольном расстоянии от нее. Для определения
координаты у используем профильную плоскость 3.
Проекции точек: D SBC; E SAB.
Проекции точек, принадлежащих плоскостям общего
положения, построим с помощью прямых линий,
принадлежащих этим плоскостям.
Так как стороны основания пирамиды являются
горизонталями для боковых граней, то для построения
проекций точек удобно воспользоваться горизонталями
плоскостей SAB и SBC, проходящими через точки D и E .
Содержание
25.
5.4а*. Построить профильную проекцию призмы.Нижнее основание ABCD 1, следовательно,
ABCD 2 , ABCD 3 и проецируется в отрезки
прямых на плоскостях 2 и 3 .
Верхняя часть прямоугольной призмы срезана
тремя фронтально проецирующими плоскостями.
Боковые грани перпендикулярны плоскости 1.
Боковые ребра перпендикулярны плоскости 1 и,
следовательно, параллельны плоскостям 2 и 3.
Для построения профильной проекции
используем координаты y и z.
Профильную проекцию строим в проекционной
связи (координата z) с фронтальной проекцией на
произвольном расстоянии от нее. Значения
координат у определяем на горизонтальной
проекции призмы.
Содержание
26.
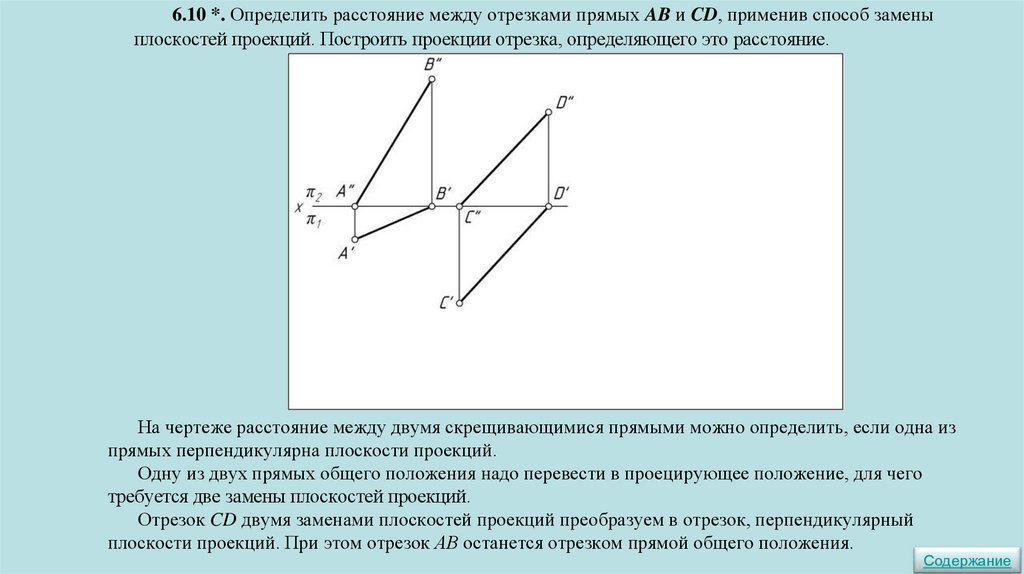
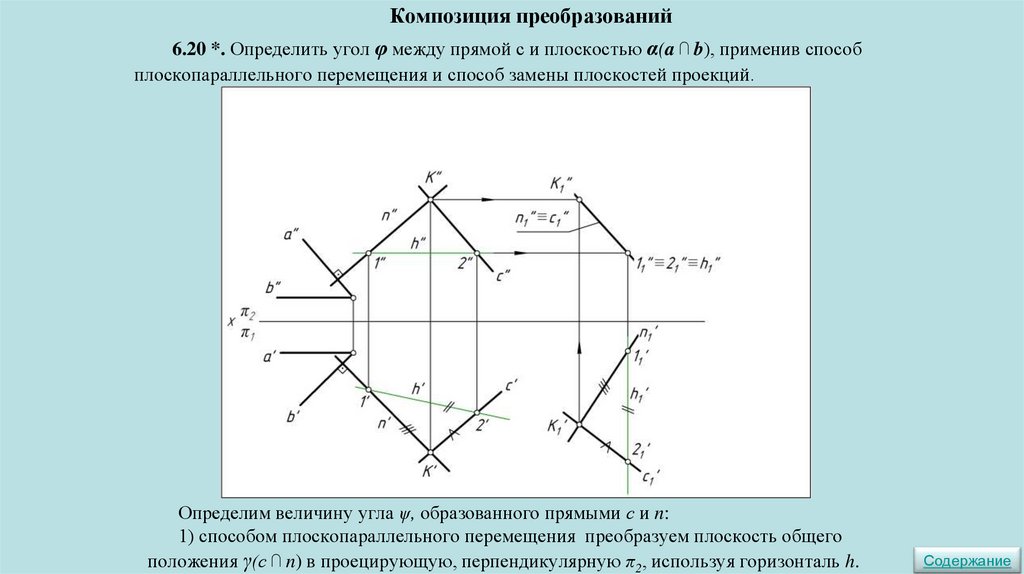
6. СПОСОБЫ ПРЕОБРАЗОВАНИЯ. МЕТРИЧЕСКИЕ ЗАДАЧИСпособ замены плоскостей проекций
6.1*. Построить проекции отрезка АВ=30 мм, принадлежащего прямой а, применив способ
замены плоскостей проекций.
Отрезок прямой проецируется без искажений на
плоскость проекций, если прямая параллельна плоскости
проекций. При этом одна проекция прямой (отрезка)
параллельна оси проекций.
Чтобы прямая общего положения заняла положение,
параллельное плоскости проекций, надо выполнить одно
преобразование.
На прямой а зададим произвольную точку С.
Заменим плоскости проекций так, чтобы новая ось
проекций х1 заняла положение, параллельное горизонтальной























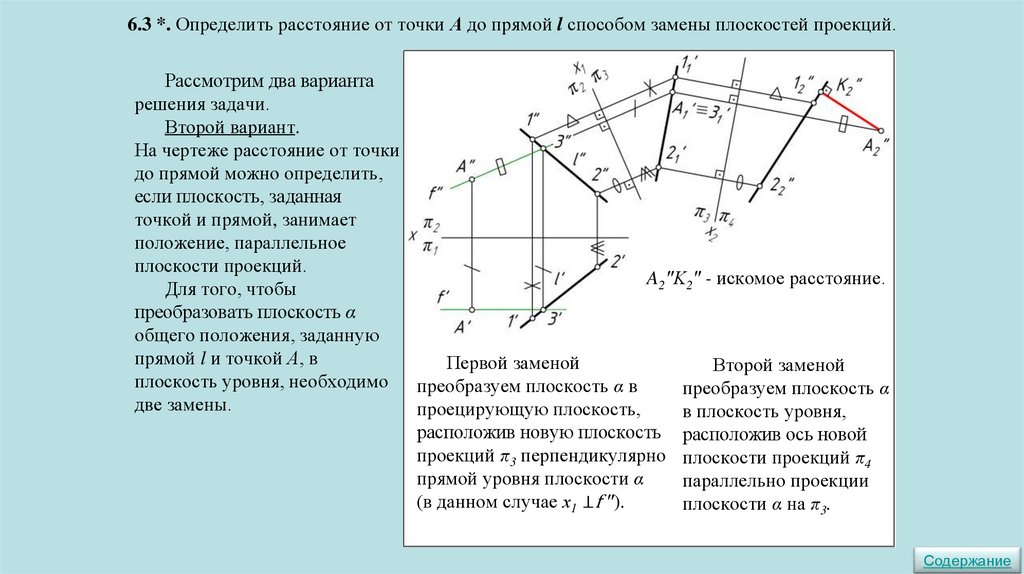





























 drafting
drafting








