Геометрические тела. Построение фигур на 3 плоскости, точка на поверхности

1. ГЕОМЕТРИЧЕСКИЕ ТЕЛА

Геометрическим телом называют часть
пространства, ограниченной
геометрическими поверхностями.
Все геометрические тела можно разделить
на две группы:
Многогранники
Тела вращения

2. Многогранники

Многогранники-тела, ограниченные со
всех сторон плоскостями.
Многогранники различают в зависимости
от формы и количества граней.

3. Призма

Призма - многогранник, у которого боковые грани
– прямоугольники или параллелограммы, а
основаниями служат два равных
многоугольника.
Если у призмы основания - правильные
многоугольники, а высота перпендикулярна
основанию, то призма – правильная и прямая.
В зависимости от количества сторон основания
призмы бывают треугольные, четырехугольные
и т. д.

4. Прямая четырехгранная призма (параллелепипед)

Верхнее основание
Боковая грань
Высота
Боковые ребра
Нижнее основание
Ребра основания

5.

Плоские фигуры, ограничивающие
многогранник, называются гранями.
Грани пересекаются между собой по
прямым линиям, которые называются
ребрами многогранника.
Ребра пересекаются в точках-вершинах
многогранника.

6. Пирамида

Пирамида-многогранник, у которого боковые
грани представляют собой треугольники,
имеющие общую вершину.
В основании у пирамиды – многоугольник. В
зависимости от количества сторон основания
пирамида называется трех-, четырех-,
пятиугольной и т. д.
Если у пирамиды основание правильный
многоугольник, а высота перпендикулярна
основанию, то пирамида правильная и прямая

7. Прямая правильная шестигранная пирамида

Боковые
Вершина
ребра
Высота
Боковая грань
Основание
Ребра основания

8. Тела вращения

Тела вращения – тела, ограниченные
поверхностью вращения

9. Прямой круговой цилиндр

Основания цилиндра – круги.
Цилиндрическая поверхность образуется
от вращения образующей вокруг оси
цилиндра.
Цилиндр, ось которого перпендикулярна к
горизонтальной плоскости проекций
называется прямым.

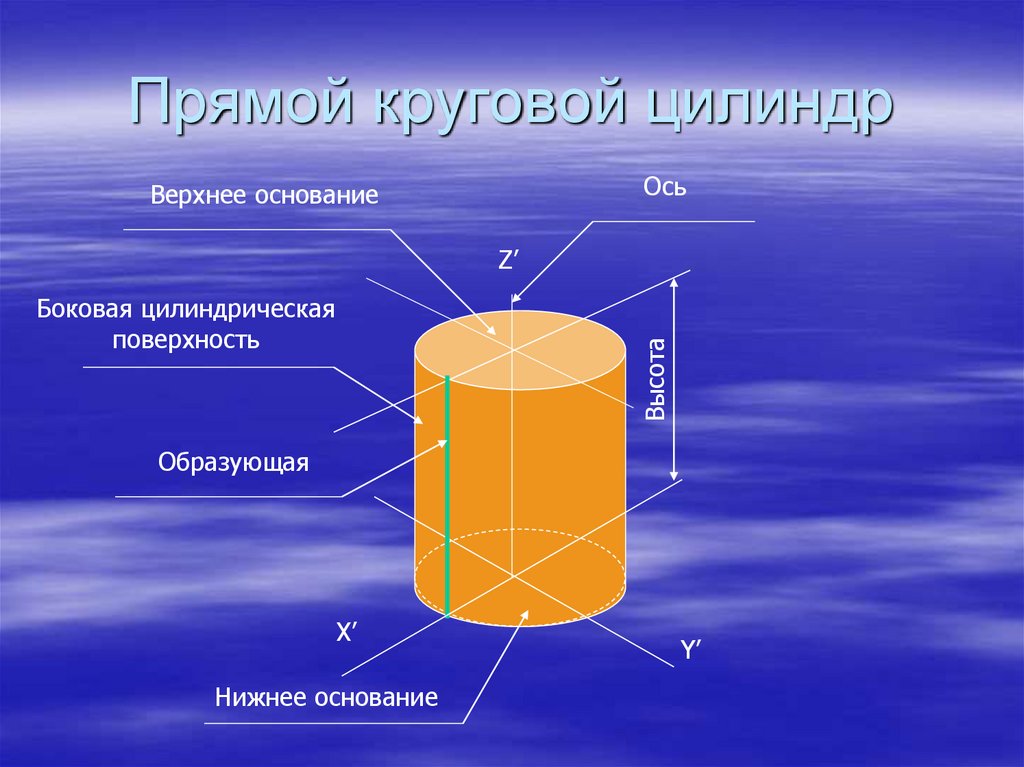
10. Прямой круговой цилиндр

Ось
Верхнее основание
Z’
Высота
Боковая цилиндрическая
поверхность
Образующая
Х’
Нижнее основание
Y’

11. Прямой круговой конус

Прямой круговой конус – тело вращения, ограниченное
конической поверхностью и плоскостью,
перпендикулярной к оси вращения.
У прямого кругового конуса коническая поверхность
образована вращением прямой линии (образующей),
пересекающей ось вращения в точке (вершине),
вокруг этой оси вращения.
Конус, ось которого перпендикулярна к горизонтальной
плоскости проекций, называется прямым.

12. Прямой круговой конус

Вершина
ось
Высота
Боковая коническая
поверхность
Z’
Образующая
X’
Основание конуса
Y’

13. Построение проекций прямого кругового конуса

Построение проекций прямого
кругового zконуса
S’
S”
х
у’
S
у

14. Построение проекций прямого кругового цилиндра

Z
х
Y’
y

15. Построение проекций правильной прямой шестигранной призмы

z
x
Y’
y

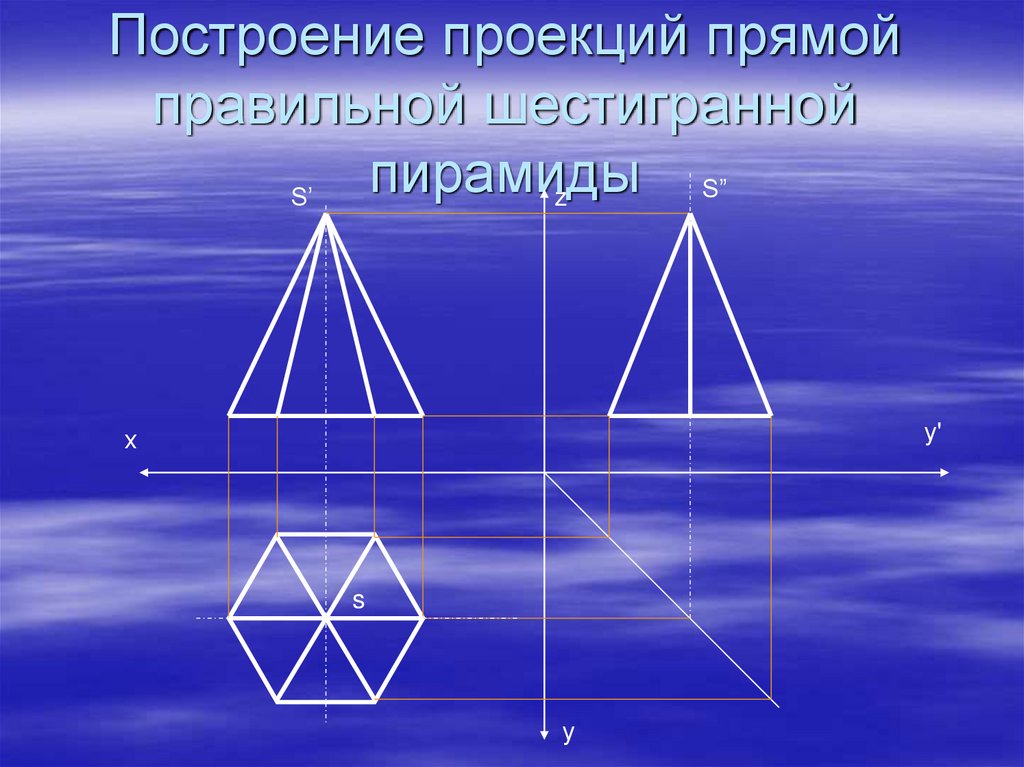
16. Построение проекций прямой правильной шестигранной пирамиды

S”
S’
z
у'
х
s
у

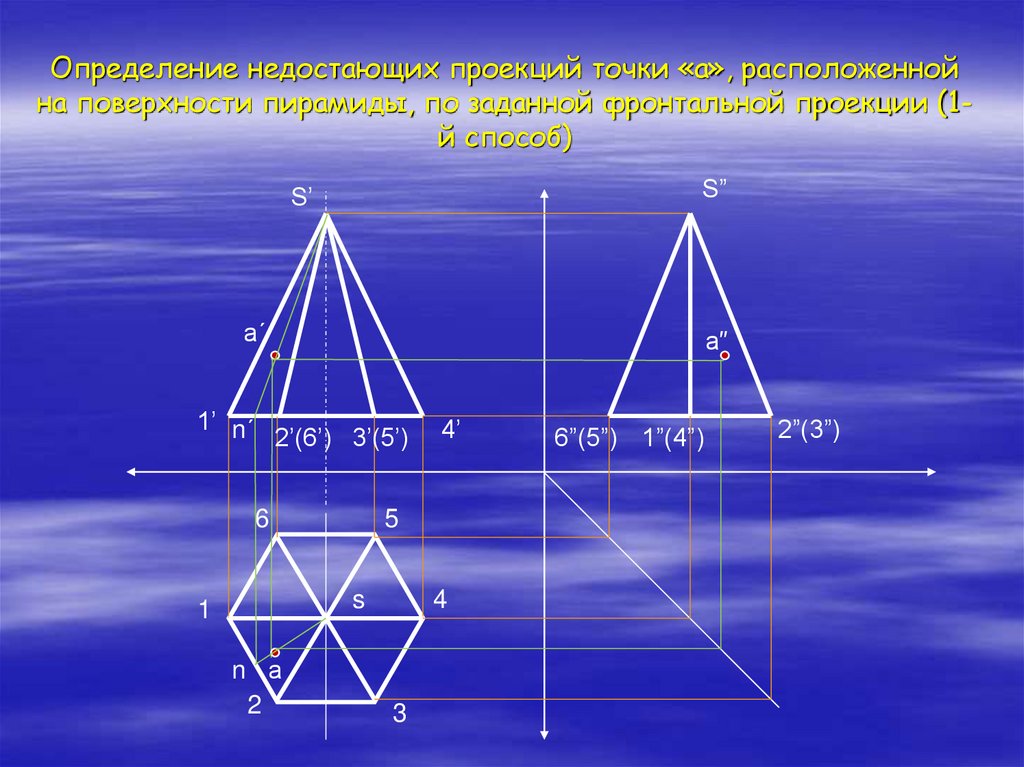
17. Определение недостающих проекций точки «а», расположенной на поверхности пирамиды, по заданной фронтальной проекции (1-й

Определение недостающих проекций точки «а», расположенной
на поверхности пирамиды, по заданной фронтальной проекции (1й способ)
S”
S’
а´
1’ n´
а″
2’(6’) 3’(5’)
6
5
s
1
n а
2
4’
4
3
6”(5”) 1”(4”)
2”(3”)

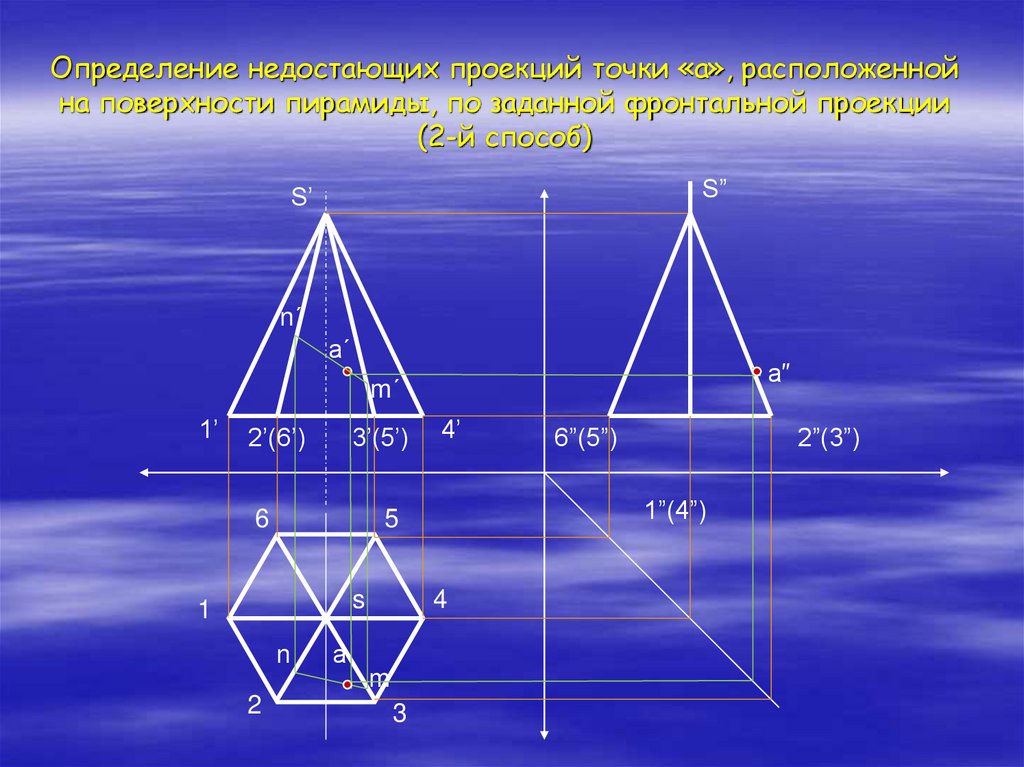
18. Определение недостающих проекций точки «а», расположенной на поверхности пирамиды, по заданной фронтальной проекции (2-й

способ)
S”
S’
n´
а´
а″
m´
1’
2’(6’)
3’(5’)
6
5
s
1
n
а
3
6”(5”)
2”(3”)
1”(4”)
4
m
2
4’

19. Определение недостающих проекций точки «а», расположенной на поверхности конуса, по заданной фронтальной проекции (1-й способ)

s’
b’
s’’
a’
c’
х
a’’
Y’
b
s
a
c

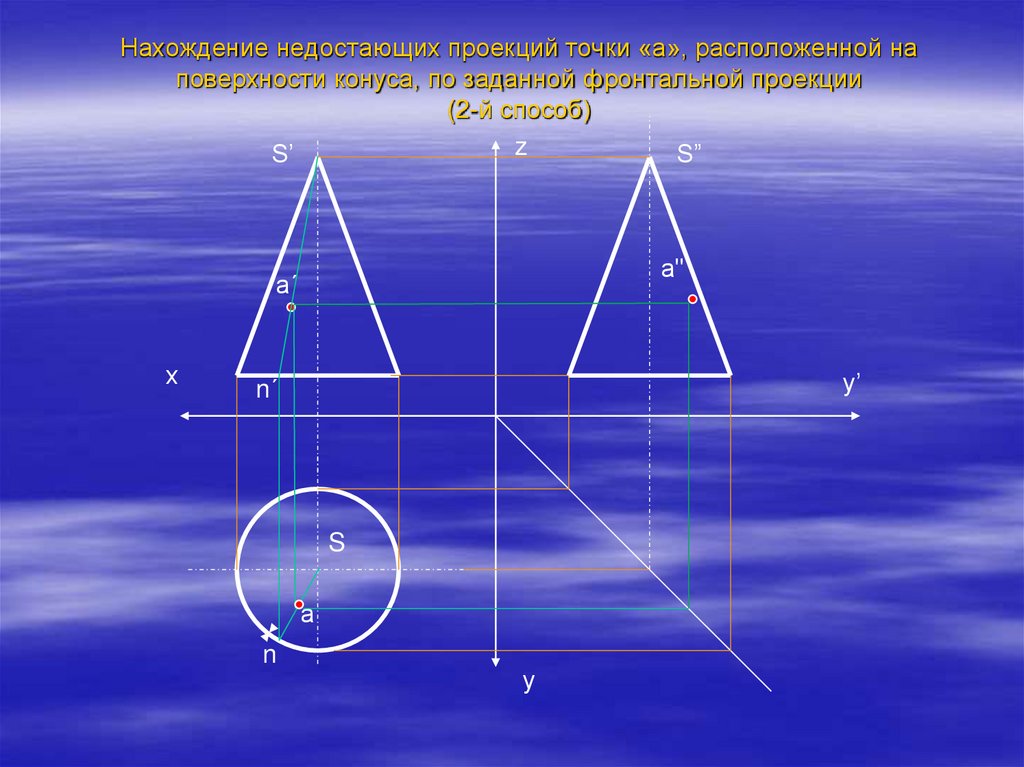
20. Нахождение недостающих проекций точки «а», расположенной на поверхности конуса, по заданной фронтальной проекции (2-й способ)

z
S’
S”
а"
а´
х
у’
n´
S
а
n
у

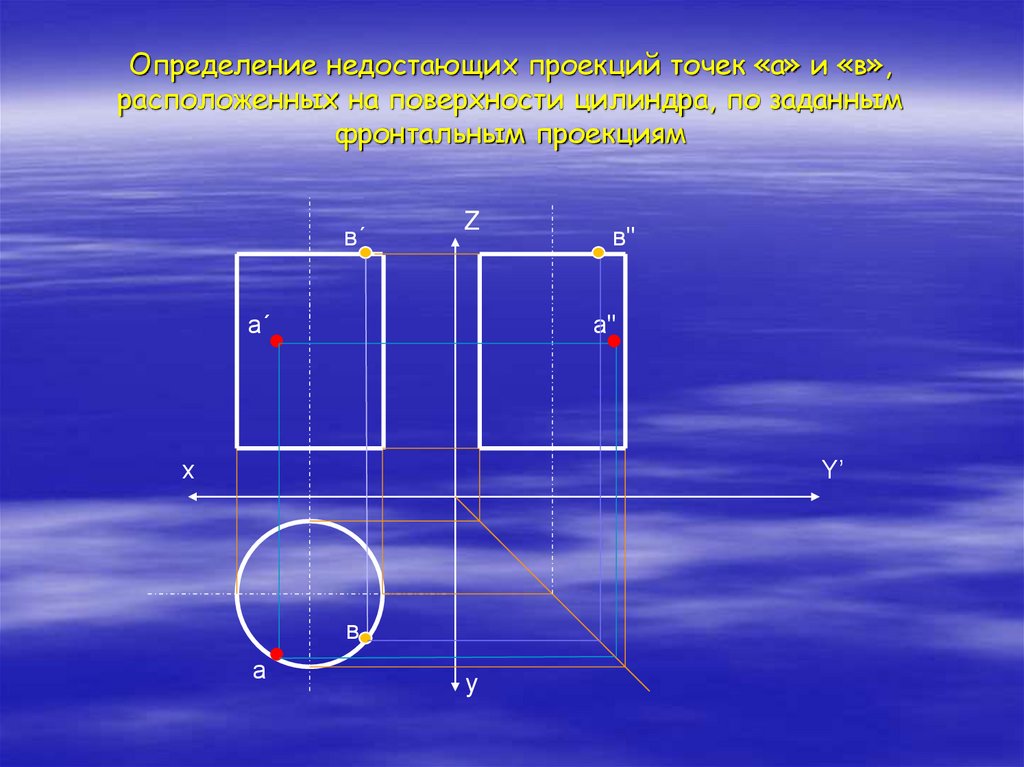
21. Определение недостающих проекций точек «а» и «в», расположенных на поверхности цилиндра, по заданным фронтальным проекциям

в´
Z
а´
в"
а"
х
Y’
в
а
y

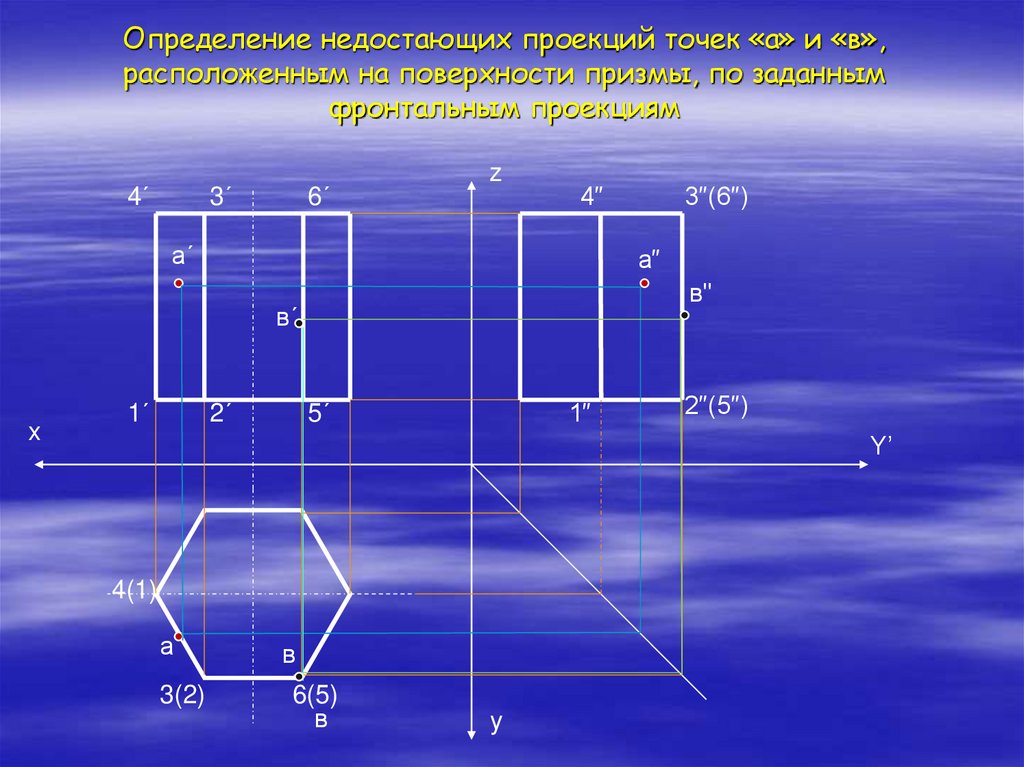
22. Определение недостающих проекций точек «а» и «в», расположенным на поверхности призмы, по заданным фронтальным проекциям

4´
3´
6´
z
4″
а´
а″
в"
в´
x
1´
3″(6″)
2´
1″
5´
2″(5″)
Y’
4(1)
а
в
3(2)
6(5)
в
y