ПЗ 12 ФР 26.11.25

1. Матричные градиентные методы: функция релаксации

x
k 1
x H J ( x )
k
k
Понятие функции релаксации позволяет
установить условие релаксационности
метода, т.е. условие монотонного убывания
ИУС
J(x):
J (x
k 1
) J (x )
k

2. Основное определение

Пусть H( ,h) есть скалярная зависимость,
отвечающая матричной функции H(J'', h) в
общей схеме градиентных методов. Здесь h
является скалярным параметром (см.,
например, МНС).
Тогда функцией релаксации метода
называется скалярная зависимость
ИУС
Rh ( ) 1 H ( , h)

3. Условие релаксационности

Для параболоида f(x) согласно общей схеме
градиентных методов имеем:
n
f ( x ) 0.5 i
k
i 1
2
i ,k
n
R ( )
k 1
ИУС
f ( x ) 0.5
i 1
2
i ,k
2
i
i

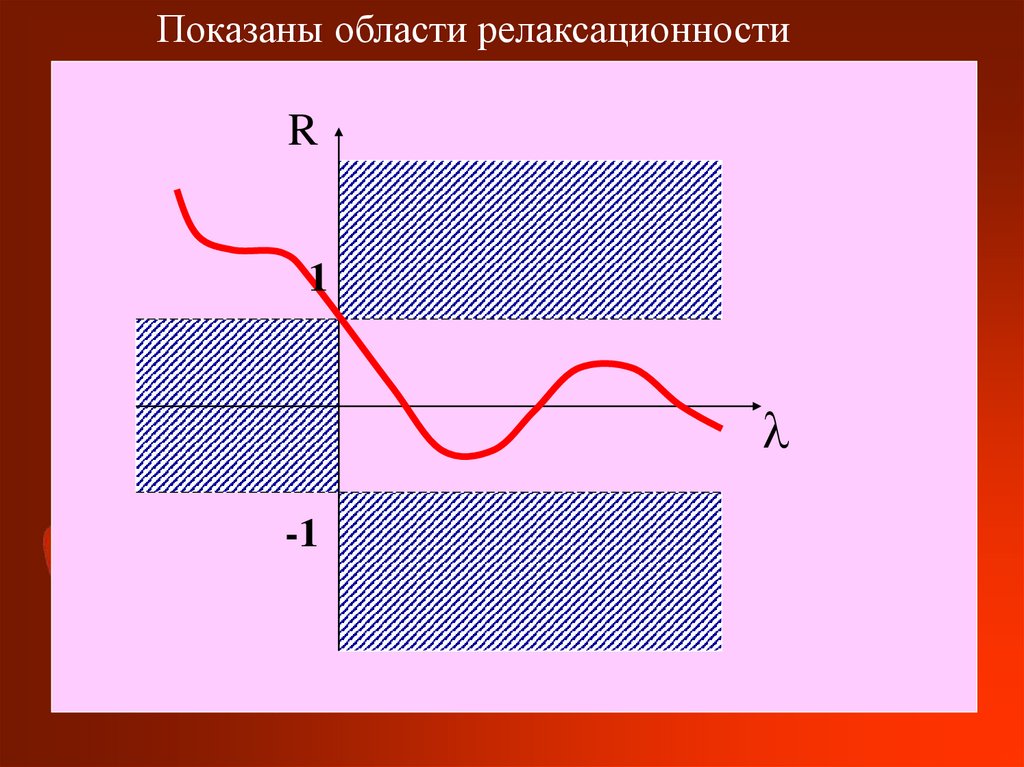
4.

Показаны области релаксационности
R
1
-1
ИУС

5. Функции релаксации классических градиентных методов

1. Простой градиентный спуск (ПГС)
R( ) 1 h
2. Метод Ньютона
R ( ) 0
3. Метод
Левенберга (метод Маркуардта,
ИУС
регуляризованный метод Ньютона)
R ( ) h /( h )

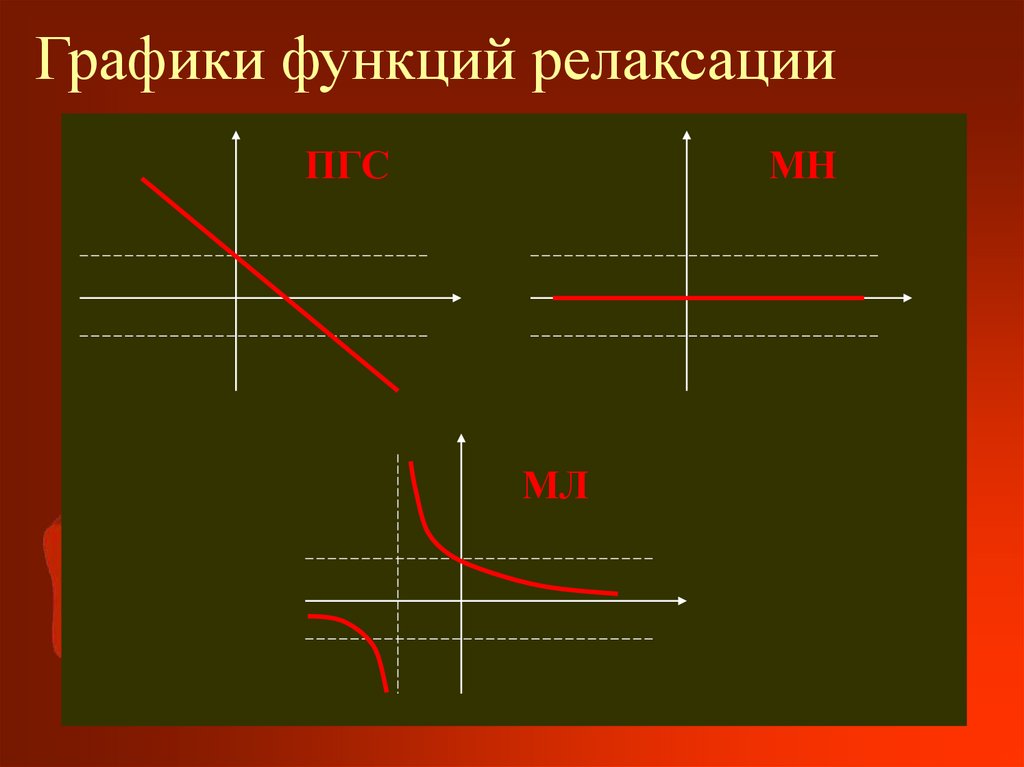
6. Графики функций релаксации

ПГС
МН
МЛ
ИУС

7. Метод Левенберга (стр. 238)

По заданной функции релаксации
R ( ) h /( h )
легко восстановить формулу самого метода:
H (1 R) (h )
1
x
k 1
ИУС
k
1
1
x (hE J ( x )) J ( x )
''
k
'
k

8. Обсуждение

• Реализация всех методов ньютоновского типа
выполняется с помощью решения систем
линейных алгебраических уравнений
• Операция обращения матрицы является
неустойчивой и редко используется в
реальных вычислениях
• Функция
релаксации является не только
ИУС
средством анализа градиентных методов, но и
средством синтеза новых методов

9. Анализ скорости сходимости метода ПГС на основе функции релаксации

1
R 1 h
m
x
ИУС
f (x
k
m i ( A) M , m 0
f ( x ) i
k 1
'
1 h i 1, i 1,..., n
-1
k
x hJ ( x )
k
Пусть J – параболоид
c А > 0:
M
1/h
k 1
2
i
) R ( i )
2
i i
2
h 2/ M

10.

Итак, имеем:
f ( x )
k
2
i i
R (1 h )
2
Если
f (x
2
h 2/ M
ИУС 2
k 1
) R ( i )
2
i i
2
- множители затухания
,
то для малых i
R 1 (см. рис.)

11. Обсуждение

• Метод ПГС сходится, вообще говоря,
медленно из-за близких к 1
множителей релаксации, отвечающих
малым собственным числам
• Чем выше степень овражности, тем
медленнее сходимость
• Были ИУС
придуманы различные методы
ускорения сходимости ПГС

12. Основное задание

• Построить матричный градиентный
метод по заданной функции релаксации
• Построить график функции релаксации
• Дать анализ сходимости и
работоспособности построенного метода
ИУС h
k
R
, h
,
h
k 10
k номер по списку