Методы оптимизации. Теория принятия решений ИУС

1.

Выбор вариантов
Часть 1. Методы оптимизации
Часть 2. Теория принятия решений
ИУС

2. Целенаправленная деятельность – это деятельность, направленная на достижение определенной цели или целей (пример с заводом)

Целенаправленная
деятельность – это
деятельность, направленная
ИУС
на достижение определенной
цели или целей (пример с заводом)

3. Схема целенаправленной деятельности

Шаг 2
Шаг 1
Шаг 3
ИУС
Многоэтапный процесс принятия
решений (выбора вариантов)

4. Современные информационные технологии (IT) и программные системы (PS) являются средством реализации различных видов и этапов

целенаправленной
деятельности
ИУС

5. Примеры целенаправленной деятельности в области разработки программных систем и информационных технологий

Примеры
целенаправленной
деятельности в области
разработки программных
систем
ИУСи информационных
технологий

6. 1. Выбор наилучшего варианта распределения ресурсов Распределение финансовых , людских и иных ресурсов между отдельными

работами,
составляющими программный
проект, с целью минимизации
ИУС
затрат и времени разработки –
основная задача менеджера
программного проекта

7.

Пример 1
…
SW Project
1. Необходимо выполнить N работ или задач,
составляющих проект
2. Каждая работа может быть начата при условии
завершения
каких-то других работ (см. рис.)
ИУС
3. Время выполнения каждой работы определяется
выделяемыми для ее выполнения средствами
(ресурсами)

8. Пример сетевого графика разработки программного проекта

Пример сетевого графика
Пример 1
разработки программного проекта
Показан критический путь
2
5
3
0
10
1
20
30
4
8
6
40
10
50
60
70
80
7
1. В кружках
показаны номера работ проекта
ИУС
2. Полное время завершения проекта определяется
критическими работами
3. Хорошо известная система Microsoft Project дает
возможность найти критический путь (анализ)
t
дни
9

9.

Пример 1
1. Оптимизируемый объект:
сетевой график разработки программного
проекта
2. Целевые (выходные) характеристики:
y1- время завершения проекта
y2- стоимость выполнения проекта
3. Выбираемые параметры:
xi – средства,
выделяемые для выполнения
ИУС
i - ой работы
Сумма xi = y2

10. Основная проблема: Как выбрать общий ресурс проекта y2, и затем распределить его между отдельными работами, чтобы выполнить

Пример 1
Основная проблема: Как выбрать
общий ресурс проекта y2, и затем
распределить его между отдельными
работами, чтобы выполнить
следующие требования
y1 < 80 дней
ИУСy < $100,000
2

11. Альтернативная формулировка основной проблемы

Имеем систему неравенств:
yi < ti
yi = Fi (X)
или:
zi > 0
ИУС
Здесь:
z i = ti – y i > 0

12. Соответствующая задача оптимизации:

J(x) = min zi
max
i
Требования к выходным
характеристикам не выполнены
z4
z3
ИУС
Выбор X
x
Требования к выходным
характеристикам выполнены
0
z1
z
z2 z5
Здесь z4 = min zi
i

13. Стандартная задача оптимизации (однокритериальная конечномерная оптимизация)

x1
x2
Объект
оптимизации
xn
J(x)
ИУС
min
x
Если имеем K(x)
max ,
то полагаем J(x) = - K(x)
и опять: J(x)
min
J(x)

14. 2. Задача оптимального проектирования Программный модуль (PM) и сама PS имеет характеристики, определяющие их качество и

соответствие спецификациям.
Предполагается, что мы можем влиять
на эти характеристики, изменяя
внутренние параметры модулей и PS.
ИУС
Требуется произвести оптимальный
выбор этих параметров.

15.

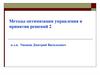
Пример 2
x1
x2
PS, PM
xn
Внутренние
(управляемые)
параметры PS (PM)
ИУС
Спецификации:
Опять неравенства !
yi < t i
y1
y2
ym
Выходные
(целевые)
характеристики,
определяющие
соответствие
спецификациям

16. 3. Выбор оптимального варианта инвестиций Заказчик требует разработать советующую программную систему, осуществляющую расчет

оптимальных инвестиций по годам
с целью
получения максимальной
ИУС
прибыли через заданный
промежуток времени

17. 4. Вообще очень часто заказчики требуют разработки программных систем, решающих определенные прикладные задачи оптимальным

образом. И из всех возможных
вариантов подобных систем и
вариантов
ИУС реализаций требуется
выбрать наилучшие (по крайней
мере, по стоимости!)

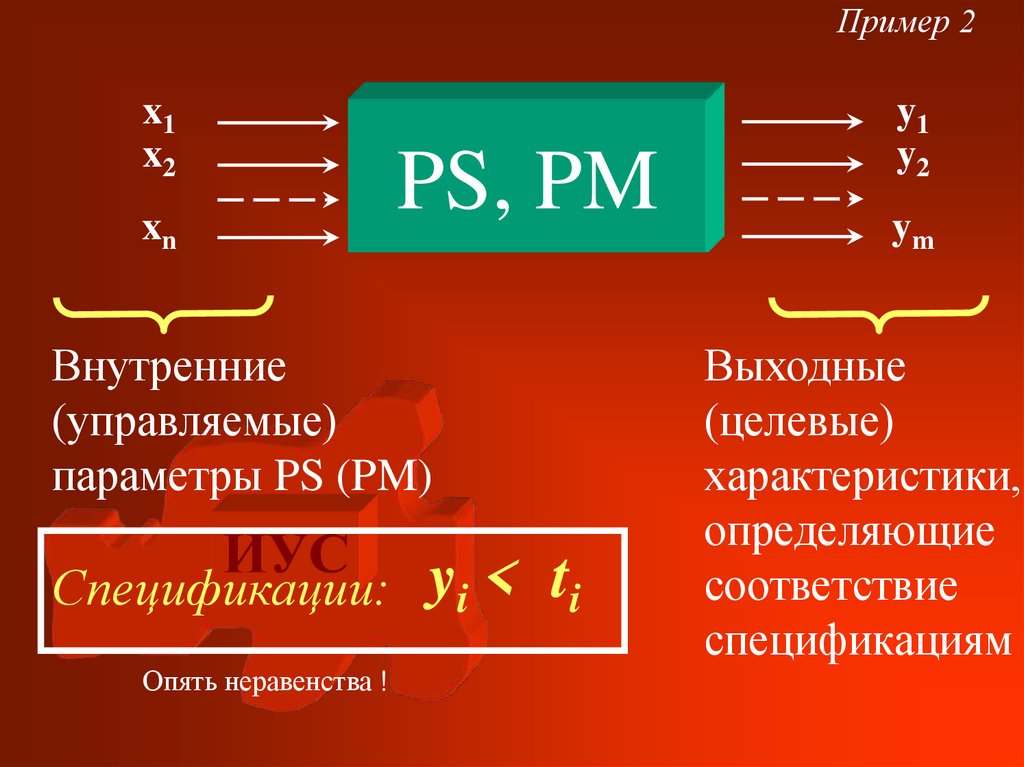
18. Состав современной информационной технологии (IT) и программной системы (PS)

IT, PS
ИУС
HW
SW
BW

19. Вы – создатели и конструкторы современных информационных технологий и программных систем

Вы – создатели и
конструкторы
современных
информационных
технологий
и
ИУС
программных систем

20. Три составляющие учебного плана:

BW – brainware: теоретическая подготовка
в области алгоритмики, математические методы,
моделирование и исследование операций
SW – software : современные технологии,
среды и средства разработки программных
проектов ИУС
HW – hardware: основы моделирования и
использования современной IT - аппаратуры

21. Аналогия с процессом приготовления пищи

IT или PS – блюдо, которое вы
готовите как повар
HW - кухонное оборудование
ИУС
SW- продукты
(мясо, молоко, овощи)
и средства их производства
BW- рецепт приготовления блюда

22. Учебный план – BW

• Численный анализ, исследование операций
• Системный анализ, моделирование,
идентификация, имитационное
моделирование
• Методы синтеза, управления и
оптимизации в теории систем,
компьютерное проектирование
• СистемыИУС
поддержки решений, системы
основанные на знаниях, экспертные
системы
• Обработка сигналов, фильтрация и т.д.

23. ЧАСТЬ 1 МЕТОДЫ ОПТИМИЗАЦИИ

ИУС

24. Основные определения

1. Оператор, отображение, функция
Однозначность
f
f
A
A
B
B
2. Функционал – частный случай функции
ИУС
A
R -множество вещественных
чисел
A
f
R

25. Постановка задачи

Задача 1.
Найти u* (минимизатор) :
u* U, J(u*) J(u), u U
J
J
min
min
ИУС
U
u
U
u

26.

Задача 2. Найти минимизирующую
последовательность {u k },
uk U :
lim J(u ) = inf J(u), k
k
J
ПРИМЕР.
ИУС
J = exp(u)
u
а) МИНИМИЗАТОР НЕ СУЩЕСТВУЕТ (задача 1 не
имеет смысла)
б) inf J(U) СУЩЕСТВУЕТ И РАВЕН НУЛЮ

27. Сходимость и некорректность

Сходимость по аргументу: lim u = u*, k
(если u* существует)
Сходимость по функционалу: lim J( uk ) = inf J(u),
J
ПРИМЕР.
u*=0
k
Из 1 следует 2
но не наоборот
ИУС
k
k
u
{u = k}- сходится по функционалу
и расходится по аргументу

28. Когда нужна сходимость по аргументу?

1. Задачи аппроксимации
ПРИМЕР : задача оптимального проектирования
x1
x2
xn
Объект
проектирования
ИУС
J(x)
min
x
J(x)
x D

29.

Точки X1 X2 одинаково
хороши по критерию J
J
J(x)
X1
X2
min
x
D
ИУС
Во множестве D выполняются все функциональные
ограничения (спецификации)
Достаточно сходимости по функционалу !

30. 2. Задачи идентификации

• Возникают, когда нас интересует именно u*, а
значение J(u) лишь косвенно отражает степень
приближения к минимизатору
• Основная цель – хорошая оценка u*
• Обычно полученная оценка u* используется далее в
других математических моделях, не связанных с
функционалом J(u)
• ПРИМЕР : оптимизация процесса полимеризации
• ЗАДАЧИИУС
ИДЕНТИФИКАЦИИ НА ПРАКТИКЕ
ВОЗНИКАЮТ ЗНАЧИТЕЛЬНО РЕЖЕ ЧЕМ
ЗАДАЧИ АППРОКСИМАЦИИ , И НАС ОБЫЧНО
ИНТЕРЕСУЕТ СХОДИМОСТЬ ПО
ФУНКЦИОНАЛУ !