Введение в дисциплину "Методы принятия управленческих решений"

1.

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ
УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ
МЕТОДЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ
РЕШЕНИЙ
Сергеев Виктор Леонидович, д.т.н., профессор кафедры АСУ
1

2.

ВВЕДЕНИЕ В ДИСЦИПЛИНУ МЕТОДЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ
РЕШЕНИЙ
Принятие управленческих решений (ПУР) рассматривается как составная часть
любой управленческой функции («подфункция» функций управления) и как
циклический (итерационный) процесс, выполняющийся по определенным
правилам:
1. Сбор, обработка и анализ информации о состоянии объекта или системы,
факторах внешней среды.
2. Обнаружение проблемы. Проблемная ситуация.
3. Идентификации проблемы. Выявление причин.
4. Определение цели функционирование системы управления (на данном
этапе выявленная проблема - причина формируется в виде цели (целей)
управленческого решения).
5. Определение критериев выбора (формирование показателей качества и критерия
эффективности либо оптимальности, разработка альтернатив).
6. Выбор оптимального решения (корректировка целей, выбор наилучшей
альтернативы, решение оптимизационных задач, оценка качества решения).
7. Реализация решения, изменения в системе управления.
8. Контроль и оценка результатов.
1,2,3,4,7 – слабо формализуемые этапы.
2

3.

ОБЩАЯ ХАРАКТЕРИСТИКА УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
Отличительные характеристики управленческих решений:
1. Цели (решение проблем конкретной организации).
2. Последствия (решение менеджера могут существенно повлиять на деятельность
организации, ее развитие, на жизнь многих людей и т.д.).
3. Разделение труда (одни менеджеры заняты, анализом ситуации, выявлением
проблем, другие постановкой целей и принятием решений, третьи их реализацией,
исполнением и контролем ).
4. Профессионализм (принятия решений в организации требует специальной
подготовки, поскольку это сложный и ответственный процесс).
Проблема принятия решений имеет междисциплинарный характер. Для
понимания сущности управленческого решения необходимо рассматривать
его основные аспекты:
1. Психологический.
2. Информационный.
3. Юридический.
4. Организационный.
3

4.

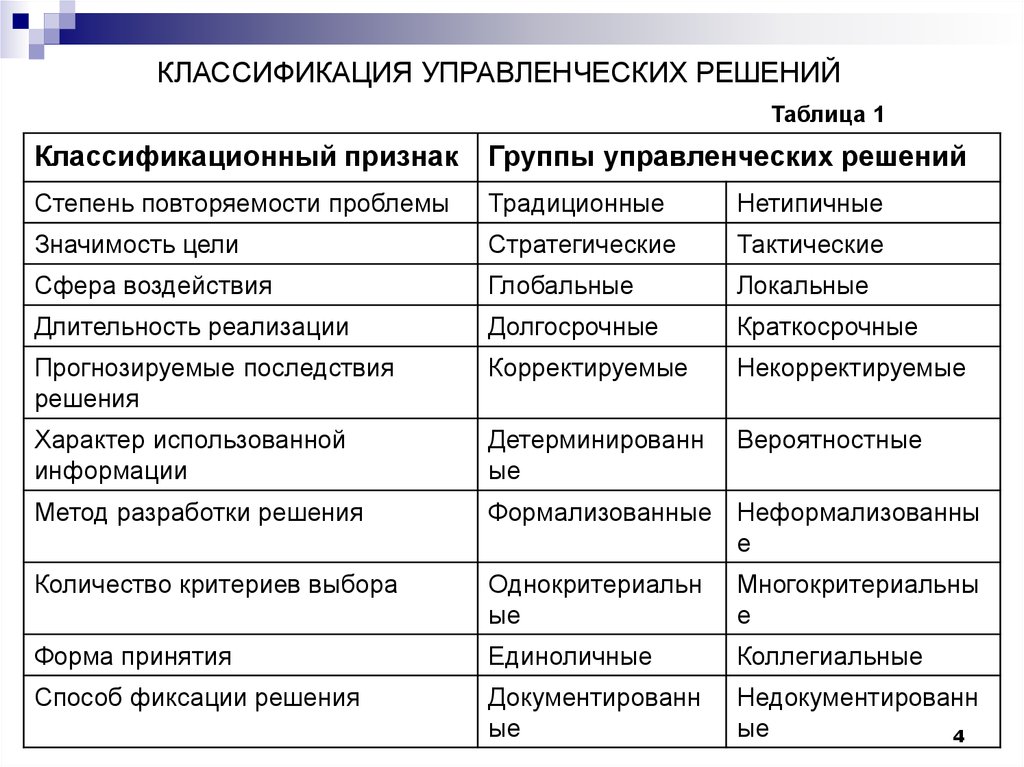
КЛАССИФИКАЦИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
Таблица 1
Классификационный признак
Группы управленческих решений
Степень повторяемости проблемы
Традиционные
Нетипичные
Значимость цели
Стратегические
Тактические
Сфера воздействия
Глобальные
Локальные
Длительность реализации
Долгосрочные
Краткосрочные
Прогнозируемые последствия
решения
Корректируемые
Некорректируемые
Характер использованной
информации
Детерминированн
ые
Вероятностные
Метод разработки решения
Формализованные Неформализованны
е
Количество критериев выбора
Однокритериальн
ые
Многокритериальны
е
Форма принятия
Единоличные
Коллегиальные
Способ фиксации решения
Документированн
ые
Недокументированн
ые
4

5.

КАЧЕСТВО И ЭФФЕКТИВНОСТЬ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
Характеристики качества управленческих решений:
1. Научная обоснованность(системный подход, компетентность и квалификация
ЛПР, достоверность информации, знание методов принятия решений).
2. Непротиворечивость(согласованность) - преемственность решений, их
соответствие стратегии, целям, ранее принятым решениям.
3. Своевременность ( учет фактора времени – например, соответствие времени
принятия решений производственным циклам).
4. Адаптивность(необходима для поддержания убывающей эффективности
решения в связи с изменением внутренних факторов и внешней среды).
5. Реальность ( учет объективных возможностей организации, ее потенциала).
1.
2.
3.
4.
5.
6.
7.
8.
Основные факторы эффективности управленческого решения:
Качество разработки (проектирования) решения.
Компетентность и опыт работы принимающего решения.
Степень информированности ЛПР.
Уровень коллегиальности в процессе разработки решения.
Удельный вес контролируемых решений.
Степень непосредственного участия руководителей и специалистов
разрабатывавших решение, в его реализации.
Мотивация исполнителей.
5
Характер и степень ответственности руководителей за результаты решения.

6. АТРИБУТЫ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ

1. Проблема. Проблемная ситуация . Цели управления.
2. Системные основы управленческих решений.
3. Интегрированные информационные среды и модели объектов
управления.
4. Показатели и критерии качества и эффективности (оптимальности).
5. Модели и алгоритмы принятия управленческих решений.
6. Системы поддержки принятия управленческих решений.
6

7. 1. ПРОБЛЕМА. ПРОБЛЕМНАЯ СИТУАЦИЯ. ЦЕЛИ УПРАВЛЕНИЯ

Проблемы не являются непосредственно
наблюдаемыми объектами. Проблемы
являются абстракциями, извлекаемые из
опыта с помощью анализа.
Рассел .Л. Акофф.
Цель – это желаемое состояние объекта управления (организации), идеальное
описание результата деятельности.
Проблемная ситуация - это состояние организации оцениваемое ее целями.
Проблема – это противоречие цели и ситуации, несоответствие целевых
показателей деятельности предприятия запланированным либо желаемым
показателям.
Типовые проблемы организации [2 ]:
1. Результаты функционирования организации в настоящий момент не
обеспечивают достижения поставленной цели.
2. Функционирование организации в будущем не обеспечит достижения
цели (целей).
3.
Изменение внешней среды или внутренних возможностей организации требует
изменение целей ее деятельности, структуры и перераспределение ресурсов.
7

8.

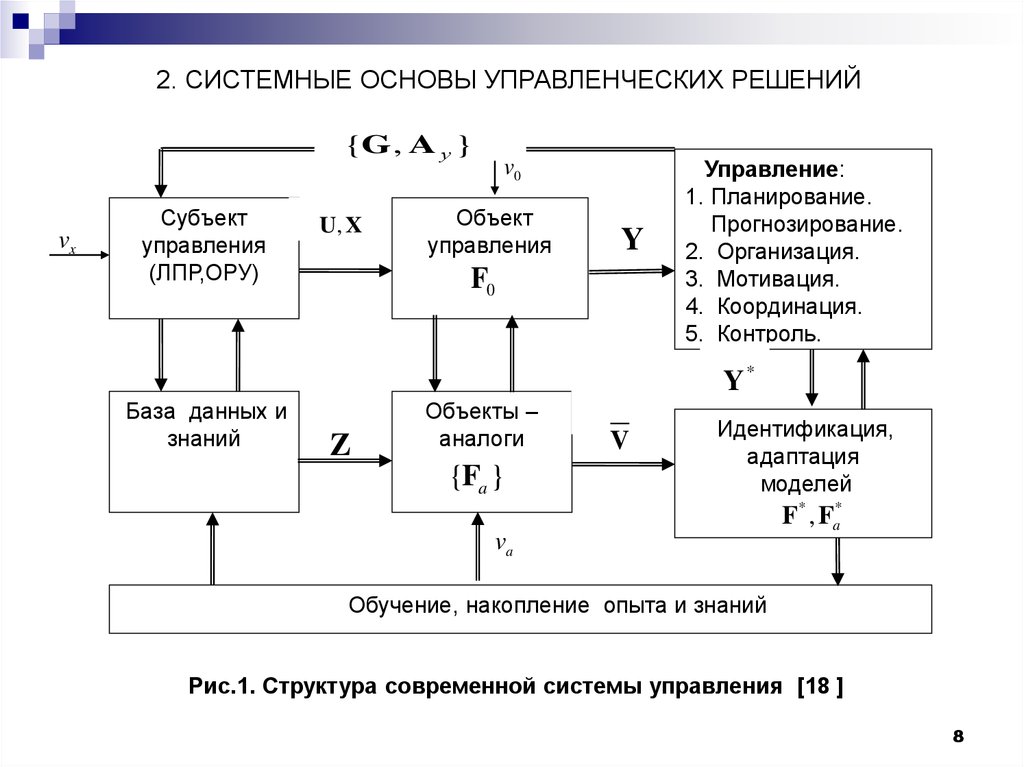
2. СИСТЕМНЫЕ ОСНОВЫ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
{G , A у }
vx
Субъект
управления
(ЛПР,ОРУ)
U, X
v0
Объект
управления
Y
F0
Управление:
1. Планирование.
Прогнозирование.
2. Организация.
3. Мотивация.
4. Координация.
5. Контроль.
Y*
База данных и
знаний
Z
Объекты –
аналоги
{Fa }
V
Идентификация,
адаптация
моделей
va
F * , Fa*
Обучение, накопление опыта и знаний
Рис.1. Структура современной системы управления [18 ]
8

9.

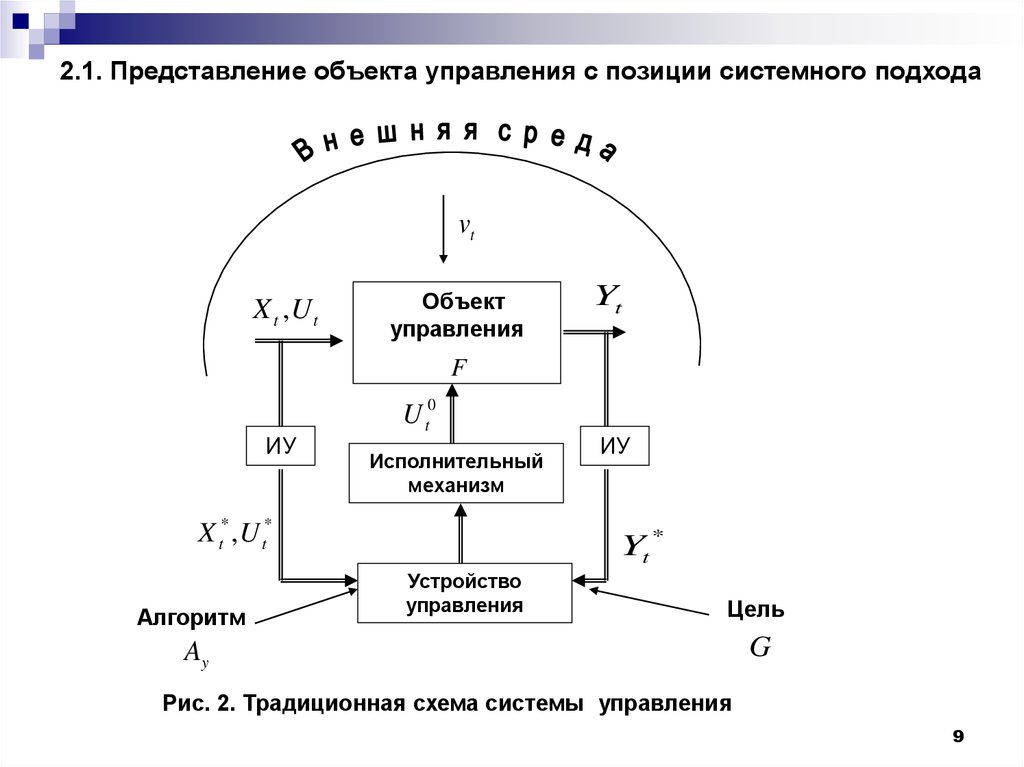
2.1. Представление объекта управления с позиции системного подхода
vt
X t ,U t
Объект
управления
Yt
F
ИУ
U t0
Исполнительный
механизм
X t* , U t*
Алгоритм
ИУ
Yt *
Устройство
управления
Цель
Ay
G
Рис. 2. Традиционная схема системы управления
9

10.

f yz
2.2. Модели объекта управления
1. Функциональная модель объекта управления (ОУ)(традиционное представление в
виде многополюсника )
(t )
X (t ),U (t )
Объект управления
Y (t )
F
Yt F (t , X (dt ),U (dt ), v, dt [t0 , t ], )
Многообразие моделей ОУ определяется многообразием оператора
(2.1)
F.
Традиционное описание системы в пространстве состояний включает пять
составляющих [10]:
1. X (t ) X t - входной сигнал как конечное множество функций времени;
2. Y (t ) Yt
3.
4.
5.
- выходной сигнал, представляющий собой конечное множество функций;
Z (t ) Z t
fy
fz
- переменные состояния;
- функционал задающий текущее состояние выходного сигнала ;
- функционал задающий значение внутреннего состояния .
Уравнение состояния и уравнение наблюдения системы:
Zt f z ( Z (t0 ), X (dt ), U (dt ), dt [t0 , t ]);
Yt f y (t , Z , X ,U , v).
(2.2)
10

11.

2.2. Модели объекта управления
Классификация моделей[5, стр. 8-14]:
1. Статические.
2. Динамические.
3. Линейные.
4. Нелинейные.
5. Непрерывные.
6. Дискретные.
7. Детерминированные.
8. Стохастические.
9. Параметрические.
10.Непараметрические.
Пример модели объекта управления:
yt* yt vt 0 u1a1 (t ) u2a2 (t ),..., umam (t ) vt ,
u j (t ), j 1, m
yt*
- факторы производства (затраты труда, капитала, информации и т. д.),
- результат производства (объем произведенной либо реализованной продукции,
потребительские свойства товара и т.п. ).
a j , j 1, m
vt
(2.3)
- параметры модели,
- случайные неконтролируемые факторы.
11

12.

2.2. Модели объекта управления
Семантическая модель современной системы управления и принятия решений
S * (t , Z ) {t ,Wf* ,Ws , G, Ty ( Ay , K y ), Р0 },
где
1. W *
f
(2.4)
{t , Y , X ,U , D* (dt ), dt [t0 , t ], v, F} - компонента (подмодель) функционального
представления ОУ;
D* (dt ) (Y * (dt ), X * (dt ),U * (dt )) - исходные данные о переменных ОУ и внешней
среды, полученные за время
12.
3.
4.
Ws
G
- компонента, определяющая структуру ОУ ;
Ty
- технология управления (ТУ) и принятия решений (ПР);
dt [t0 , t ] ;
- подсистема целей (иерархия, дерево целей);
Aу {Z , Opt (Ф, К opt )}- алгоритм управления и принятия решений;
ZФ
множество альтернатив;
Opt - критерий качества (эффективности) либо
принцип оптимальности;
- вектор существенных свойств системы;
альтернативы
z Z ;
0
K opt
- правило выбора наилучшей
K y - комплекс условий, обеспечивающий качество и эффективность алгоритма Ay ;
5.
P0 - предикат целостности, определяющий назначение системы, семантику ее
компонент.
12

13.

3. ПРОБЛЕМА ИНТЕГРАЦИИ ИНФОРМАЦИИ. ПОНЯТИЕ ОБЪЕКТА – АНАЛОГА
В процессе управления и принятия решений должна быть использована
разнообразная информация:
(*)
1. Исходные данные Y * , X * ,U * .
2. Дополнительные априорные сведения, знания и опыт ЛПР (экспертные оценки,
косвенные наблюдения переменных ОУ и внешней среды и т.п.) Y , X , U .
3. Информация о структуре оператора ОУ и объектах - аналогах F0 , Fa .
4. Информация о статистических характеристиках случайных неконтролируемых
переменных vx , v0 , va .
Для интеграции и учета всей имеющейся информации (*) требуется развитие
семантической модели системы управления (2.4 см. слайд 12).
Семантическая интегрированная система моделей объекта управления:
*
S
o
,t So (t , Z o ),
*
Su (t , m)
{So* (t , Z o ), S a , j (t , Z a , j ), j 1, m}, (3.1)
S a ,t S a (t , So (t , Z o ), Z a ).
Sa,t (t , S aj , j 1, m)
- семантические информационные модели объектов- аналогов, представляющих
дополнительную априорную информацию, накопленный опыт и знания;
m - параметр сложности модели; Z o , Z a - переменные (в общем случае подсистемы) ОУ и АО.
13

14.

3. ПРОБЛЕМА ИНТЕГРАЦИИ ИНФОРМАЦИИ. ПОНЯТИЕ ОБЪЕКТА – АНАЛОГА
vo , t
X t* ,U t*
ОБЪЕКТ УПРАВЛЕНИЯ
Система (3.2) следует из (3.1) при:
Yt *
F0 (t , X * ,U * )
*
*
1. So,t Yt .
2. So F .
3. Z o ( X t ,U t , o ).
Z a ,t
ОБЪЕКТ- АНАЛОГ
Fa (t , Z a )
va ,t
Vt
4.
Sa V.
5.
Sa Fa .
6. Z a Z a .
Рис. 3. Представление объекта управления и объекта аналога
Интегрированная система моделей ОУ и объекта- аналога (ОА) ([ 5] стр. 15-17):
*
*
*
Y
(
t
)
F
(
t
,
X
,
U
, v0 ),
0
V t Fa (t , Z 0 , Z a , va ),
(3.2)
F0 , Fa - модели (операторы) объекта управления и объекта аналога;
Z0 (Y , X ,U ), Z a - входные переменные объекта управления и объекта – аналога;
V t - дополнительные априорные данные;
vo ,t , va ,t
- случайные факторы.
14

15.

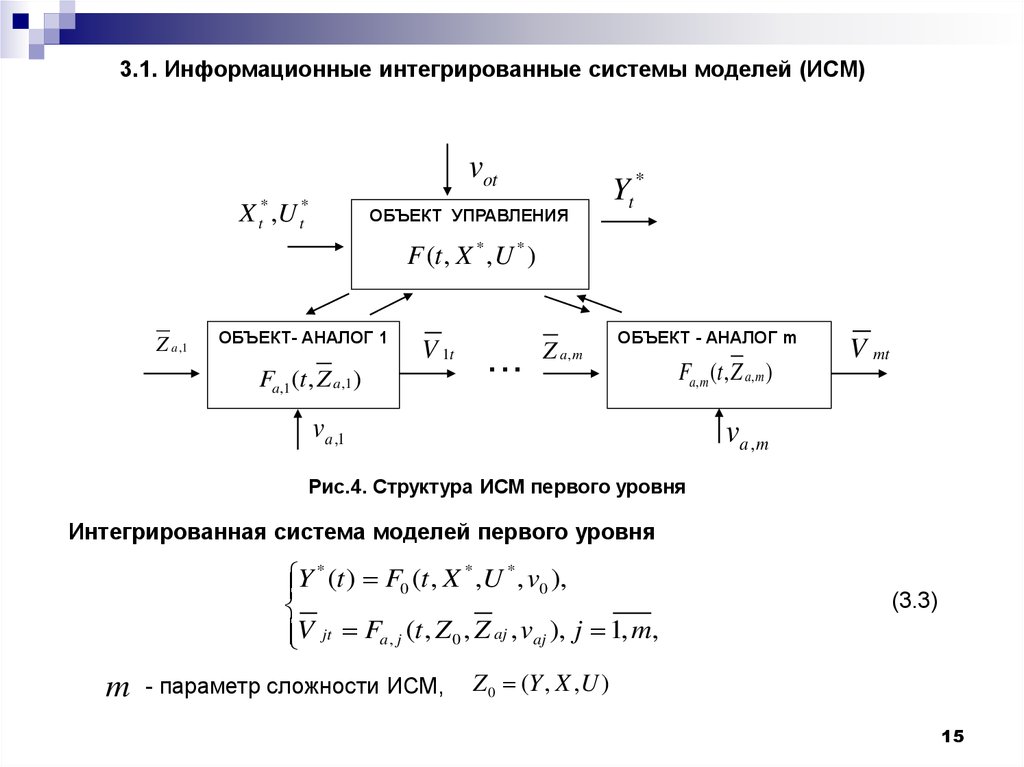
3.1. Информационные интегрированные системы моделей (ИСМ)
vot
X t* ,U t*
ОБЪЕКТ УПРАВЛЕНИЯ
Yt *
F (t , X * , U * )
Z a ,1
ОБЪЕКТ- АНАЛОГ 1
V 1t
Fa,1 (t , Z a,1 )
...
Z a,m
ОБЪЕКТ - АНАЛОГ m
Fa, m (t, Z a,m )
va ,1
V mt
va , m
Рис.4. Структура ИСМ первого уровня
Интегрированная система моделей первого уровня
*
*
*
Y (t ) F0 (t , X ,U , v0 ),
V jt Fa , j (t , Z 0 , Z aj , vaj ), j 1, m,
m
- параметр сложности ИСМ,
(3.3)
Z0 (Y , X ,U )
15

16.

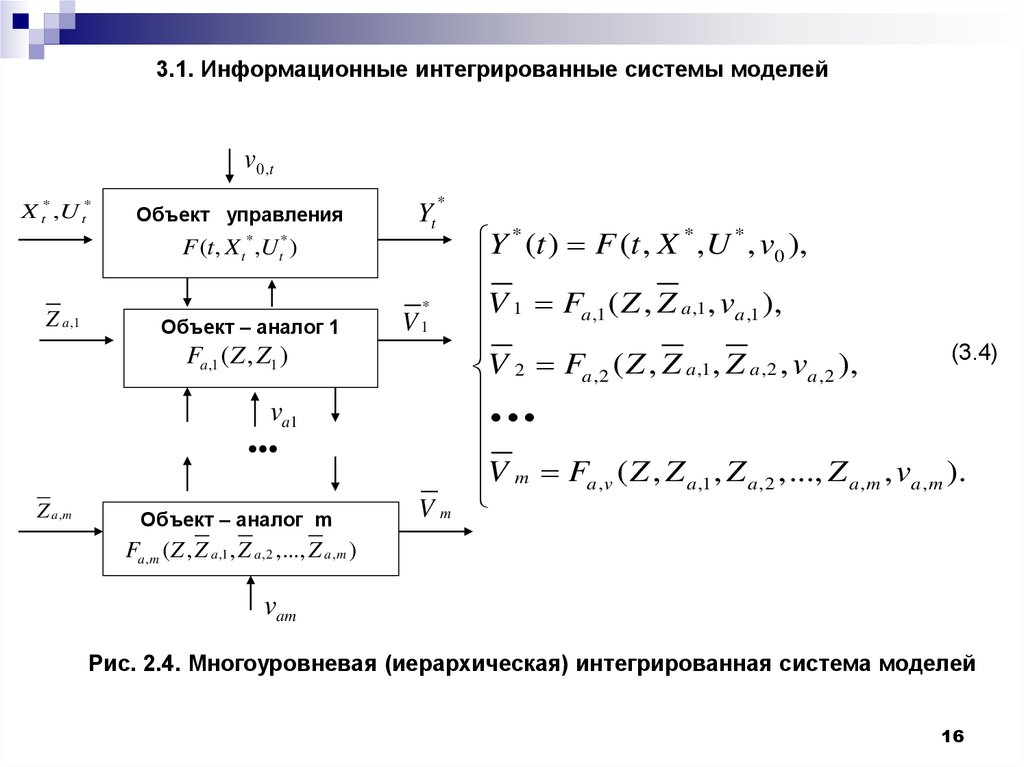
3.1. Информационные интегрированные системы моделей
v0,t
X t* ,U t*
Объект управления
Yt
*
F (t, X t * ,Ut* )
Z a ,1
Объект – аналог 1
V
*
1
Fa ,1F(1Z( Z, Z1 )1 )
va1
●●
Z a,m
Объект – аналог m
Vm
Y * (t ) F (t , X * , U * , v0 ),
V 1 Fa ,1 ( Z , Z a ,1 , va ,1 ),
(3.4)
V 2 Fa ,2 ( Z , Z a ,1 , Z a ,2 , va ,2 ),
V F ( Z , Z , Z ,..., Z , v ).
m
a ,v
a ,1
a ,2
a ,m
a ,m
Fa , m ( Z , Z a ,1 , Z a ,2 ,..., Z a ,m )
vam
Рис. 2.4. Многоуровневая (иерархическая) интегрированная система моделей
16

17.

3.2. Интегрированные системы моделей показателей деятельности предприятия
(ПДП) с учетом факторов внешней среды
Модельная основа ПДП. Многоуровневая интегрированная динамическая система
моделей (многоагентная, многомодельная информационная среда - ММИС) [15])
Yt * F (t , Y * (dt ), X * (dt ), U * (dt ), v0 ),
(3.5)
V 1, j ,t F1 j (t , V 1, j (dt ), Z 1, j (dt ), Z o (dt ), va , j ), j 1, m,
V 2, j , k F2, j , k (t , V 2, j , k (dt ), Z 2, j , k (dt ), Z 1 j ( dt ), Z o ( dt ), va , j ,k ), k 1, l j , dt [t0 , t ]
Примеры моделей ПДП.
1. Интегрированная система моделей производственных функций:
yt* f (t , U , a ) 0 u1 1 (t ) u2 2 (t ),..., um m (t ) v0t , t 1, n,
T
V j f (t , U , a ) d t va ,1, j , y t k f (t n k , U , a ) va ,2 , j 1, m, k 1, l ,
t0
V j , j 1, m
(3.6)
- экспертные оценки емкости рынка;
y n k , k 1, l - экспертные оценки прогнозных значений объемов реализованной
продукции.
17

18.

f (t , α)
3.2. Системы моделей показателей деятельности предприятия (ПДП) с учетом
факторов внешней среды
2. Интегрированная система моделей жизненного цикла товара с учетом экспертных
оценок емкости рынка [5,16-17]:
yt* yt v0t f (t , a ) v0t , t 1, n,
T
V j V (a ) vaj f (t , a )dt vaj , j 1, l ,
t0
(3.7)
f (t , a) a1 exp( a2t )t a3 - малопараметрическая модель жизненного цикла товара (пример).
3. Интегрированная система моделей добычи нефти с учетом экспертных оценок
извлекаемых запасов имеет вид 3.7 где:
yt* Qí* (t ) - фактические значения добычи нефти ;
V j , j 1, l - экспертные оценки извлекаемых запасов.
4. Интегрированная система моделей текущей емкости рынка
экспертных (прогнозных) оценок [17]:
Vt * Vt v0t , t 1, n,
V (tn k ) V (tn k ) ak , k 1, l.
Vt с учетом
(3.8)
18

19.

4. ПОКАЗАТЕЛИ И КРИТЕРИИ КАЧЕСТВА И ЭФФЕКТИВНОСТИ (ОПТИМАЛЬНОСТИ)
Показатель – характеристика отражающая качество системы (алгоритма) управления и
принятия решений или целевую направленность процесса принятия решений (операции).
Примеры показателей качества (либо эффективности) :
1. Выходные (зависимые) переменные объекта управления (объем выпускаемой
продукции, ее качество, объем продаж, услуг, темп роста объема продаж и т.д.)
Y (t ) ( yk (t ), k 1, n).
4.1
2. Выходные переменные объектов - аналогов (емкость рынка, прогнозные значения
объемов реализованной продукции, прогноз цен, текущая емкости рынка и т.д.)
V (V j , j 1, m)
4.2
3. Функции (функционалы) от переменных объектов управления, объектов –
аналогов, исходных данных и дополнительных априорных сведений (целевые функции,
функции качества, эффективности, полезности, выигрыша, потерь и т.д.)
Фk (Z ) Фк (t , Y , X ,U , D* ,V , G), k 1, l.
4.3
Обобщенный показатель качества системы управления представляет вектор ее
существенных свойств
Ф (Фk (Z ), k 1, l ).
4.4
19

20.

4. ПОКАЗАТЕЛИ И КРИТЕРИИ КАЧЕСТВА И ЭФФЕКТИВНОСТИ (ОПТИМАЛЬНОСТИ)
Примеры показателей существенных свойств систем управления[10]:
1. Показатели качества:
1.1. общесистемные свойства - целостность, устойчивость, наблюдаемость,
управляемость, открытость, динамичность и др.;
1.2. структурные свойства - состав, связность, организация, сложность, масштабность,
централизованность, объем и др.;
2. Показатели эффективности:
функциональные (поведенческие, операционные) свойства – результативность (Э) ,
ресурсоемкость(r), оперативность (O),мощность, мобильность, производительность и др.
Уровни качества систем управления и принятия решений в порядке возрастания их
сложности [10]:
1. Устойчивость (прочность, стойкость к воздействиям(робастность), живучесть).
2. Помехоустойчивость(надежность, пропускная способность, эффективное кодирование/
декодирование).
3. Управляемость (точность, гибкость, наблюдаемость);
4. Способность – потенциальная эффективность функционирования идеальной системы
(результативность (производительность, мощность), ресурсоемкость, оперативность);
5. Самоорганизация(свобода выбора решений, адаптируемость, самообучаемость, способность к
20
распознаванию ситуаций, накопление опыта и знаний ).

21.

4. ПОКАЗАТЕЛИ И КРИТЕРИИ КАЧЕСТВА И ЭФФЕКТИВНОСТИ (ОПТИМАЛЬНОСТИ)
Нормированные показатели качества систем:
yk (t )
y (t ) * , k 1, n,
yk (t )
4.4
н
k
yk* (t )
- «идеальное» значение показателя .
Подходы к выбору нормированных показателей:
1. Предпочтение ЛПР.
2.
3.
yk* (t ) max yk (t ).
yk* (t ) max yk (t ) min( yk (t ).
Определение идеальной системы (алгоритма) при заданном комплексе условий
K opt : Ф( z 0 ) Opt (Фk ( z), k 1, l )
K y0
4.5
z Z
В (4.5) все частные показатели качества достигают оптимума (максимальны либо
минимальны) .
Для вероятностной (стохастической) системы
K opt : MФ( z 0 ) Opt (MФk ( z ), k 1, l ),
z Z
M- символ математического ожидания.
4.6
Opt Фk ( z ) max Фk ( z )[min Фk ( z )]
z Z
z Z
z Z
21

22.

4. ПОКАЗАТЕЛИ И КРИТЕРИИ КАЧЕСТВА И ЭФФЕКТИВНОСТИ (ОПТИМАЛЬНОСТИ)
Критерий пригодности системы
К приг : Фk ( z* ) kдоп
Фkдоп Фk0
, k 1, l ,
0
Фk
4.7
k - радиус области пригодности(адекватности);
Фkдоп , Фk0 Фk0 ( z 0 )
- допустимые и оптимальные значения частных показателей качества.
22

23.

4. ПОКАЗАТЕЛИ И КРИТЕРИИ КАЧЕСТВА И ЭФФЕКТИВНОСТИ (ОПТИМАЛЬНОСТИ)
Эффективность процесса управления и принятия решений определяется
степень его приспособленности к достижению цели – исхода операции
(эффективность зависит как от свойств системы управления, так и от внешней среды)
Пример обобщенного показателя эффективности (ПЭ) - исхода операции
Фэф ( Z ) (Фэ ( Z ), Фr ( Z ), Ф0 ( Z )),
Фэ ( Z ) - результативность, Фr ( Z ) - ресурсоемкость, Ф0 (Z ) - оперативность.
4.8
Типы показателей качества (ПК) и эффективности систем управления:
1. Детерминированные (ПК и ПЭ - неслучайные величины).
2. Вероятностные (ПК и ПЭ - случайные величины с известными законами распределения).
3. Неопределенные (ПК и ПЭ- случайные величины с неизвестными законами распределения).
Требования к показателям качества и эффективности:
1. Соответствие цели (для каждой цели должен быть показатель(показатели) эффективности).
2. Полнота (ПК и ПЭ должны отражать как желательные (целевые) так и нежелательные (побочные)
последствия операции).
3. Измеримость составляющих ПК и ПЭ с помощью натурного эксперимента либо модели операции.
4. Ясность физического смысла(измерение с помощью доступных для восприятия количественных
мер).
5. Неизбыточность (стремление к минимизации размерности ПК и ПЭ).
6. Чувствительность к изменениям значений управляемых характеристик.
23

24.

4. ПОКАЗАТЕЛИ И КРИТЕРИИ КАЧЕСТВА И ЭФФЕКТИВНОСТИ (ОПТИМАЛЬНОСТИ)
1. Показатели, критерии качества и эффективности в условиях определенности
Общая задача векторной оптимизации:
Ф( z* ) Opt (Фk ( z ), k 1, l ).
4.9
z Z
Задача (4.9) решается путем использования разных методов устранения
многокритериальности (например, свертывания векторного критерия в скалярный):
l
Ф( z ) Opt (Ф( z ) h jФнj ( z ))
*
z Z
4.10
j 1
h j - параметр важности («вес») частного нормированного показателя качества
Фнj ( z)
Форма представления оптимального решения [5,6]
z * arg min(max)Ф( z );
z Z
Ф( z * ) min(max)Ф( z ).
z Z
4.11
Примеры частных показателей эффективности (средних потерь) :
T
1
Ф( z ) r ( у (t ) z (t ))dt
Т 0
r ( x)
1 n
Ф( z ) r ( у (ti ) z (ti ))
n i 1
- функция потерь ( r ( x) x2 , r ( x) x ) .
4.12
24

25.

4. ПОКАЗАТЕЛИ И КРИТЕРИИ КАЧЕСТВА И ЭФФЕКТИВНОСТИ (ОПТИМАЛЬНОСТИ)
1.1. Основные методы решения задач векторной оптимизации [6,10,11] :
1. Метод выделения главного критерия - условная оптимизация(назначается главный
показатель, остальные выводятся в состав ограничений):
Ф( z* ) Opt Ф1 ( z ); Фi ( z ) Ci , i 2, 3,..., l.
(*)
z Z
2. Метод лексикографической оптимизации(2.1. все частные показатели качества упорядочены
по важности в порядке возрастания их номеров –
Ф( r ) , r 1, 2, 3,..., l;
2.2. поиск решения осуществляется по схеме:
Z
*
(1)
Z
*
(2)
Z , Ф( z*(1) ) OptФ(1) ( z);
z Z
z (1) , Ф( z (2) ) Opt Ф(2) ( z );
*
*
(**)
z Z *(1)
Z
*
(l )
z *( l 1) , Ф( z *( m ) ) Opt Ф( l ) ( z );
z Z *(l 1)
Z (*r ) - наилучшее решение по показателю Ф( r ) .
3. Метод последовательных уступок - 3.1. для каждого частного критерия назначается
допустимое отклонение Ф( r ) deltar , r 1, 2, 3,..., m; 3.2. поиск решения осуществляется по схеме (**).
4. Методы свертывания векторного критерия в скалярный (наиболее часто используется
аддитивная свертка векторного показателя качества в скалярный (4.10)).
5. Нахождение паретовского множества (способ состоит в отказе от поиска единственной
«наилучшей» альтернативы : в результате попарного сравнения все худшие по всем критериям
25
альтернативы отбрасываются)[11].

26.

4. ПОКАЗАТЕЛИ И КРИТЕРИИ КАЧЕСТВА И ЭФФЕКТИВНОСТИ (ОПТИМАЛЬНОСТИ)
2. Показатели и критерии качества и эффективности в условиях риска
Операции выполняемые в условиях риска являются вероятностными ( однозначность
исходов нарушается)
Общая задача векторной оптимизации в условиях риска:
Pr Ф( z* ) Opt (Pr Фk ( z ), k 1, l )
4.13
z Z
Pr ( M , D, P, f ,...) - символы вероятностной операции - среднего, дисперсии, вероятности и т.п.
Частных показатели и критерии в вероятностных операциях (примеры) :
m
Pr Ф( z ) ( р( уk / zi )r ( уk zi ), i 1, n)
p( уk / zi )
k 1
- условная вероятность исхода операции y (tк ) ;
Pr Ф( z ) f ( у1 , y2 ,..., уm / z )
f
- функция правдоподобия случайных величин
4.15
yi , i 1, n .
z 0 arg max f ( z )
z Z
z0
4.14
- оптимальная альтернатива (оценка) метода максимального правдоподобия.
4.16
26

27.

4. ПОКАЗАТЕЛИ И КРИТЕРИИ КАЧЕСТВА И ЭФФЕКТИВНОСТИ (ОПТИМАЛЬНОСТИ)
3. Показатели и критерии качества и эффективности в условиях неопределенности
Общая задача векторной оптимизации в условиях неопределенности:
Ф( z* ) Opt (Фk* ( z, x), k 1, l ),
z Z
4.17
Фk* ( z , x) - оценки показателей качества (эффективности) Фk ( z , x) ;
x ( x1 , x2 ,..., xn )
- переменные состояние среды.
Показатели качества и критерии оптимизации в условиях неопределенности (примеры) :
1. Показатели качества моделей жизненного цикла продукции (3.8) с учетом экспертных оценок
емкости рынка:
n
l
Ф(a) ( J 0 , J a ) ( ( yt* f (t , a))2 , h j (V j V (a)) 2 ).
t 1
j 1
4.18
Матричная форма (4.18)
2
Ф(a) ( Y* F(t , a) , (V S (T , a))T W (h)(V S (a))),
Y* , F, V - векторы, X
- норма X ; W (h) diag (h j , j 1, m) - диагональная матрица.
n
Ф(a) ( y f (t , a) ,
t 1
*
t
l
V
j 1
j
S (a) ).
4.19
27

28.

4. ПОКАЗАТЕЛИ И КРИТЕРИИ КАЧЕСТВА И ЭФФЕКТИВНОСТИ (ОПТИМАЛЬНОСТИ)
4.1. Критерии качества и эффективности в условиях неопределенности [6,10,11] :
1. Критерий Лапласа (состояния среды равновероятные)
K
opt
: Ф( z ) max(
*
i
p
Ф( z , x
n
1
i
j 1
j
4.20
).
2. Максиминный критерий (критерий осторожного наблюдателя Вальда - выбор «наименьшего из зол»)
K opt : Ф( z * ) max min Ф( zi , x j ), i 1, m, j 1, p).
4.21
j
i
3. Критерий минимального риска (Сэвиджа)
K opt : Ф( z * ) max min[ Ф( zi , x j ) (max Ф( zi , x j ) Ф( zi , x j )), i 1, m, j 1, p)].
j
i
i
4. Критерий пессимизма- оптимизма (критерий Гурвица)
K opt : Ф( z * ) max[ a max Ф( zi , x j ) (1 a ) min Ф( zi , x j )].
i
4.22
4.23
j
j
Матрица эффективности программных продуктов
Таблица 2
Фj
zi
z1
z2
z3
1.
Критерий Лапласа
Ф1
Ф2
Ф3
Ф4
2.
Критерий Вальда
0,1
0,5
0,1
0,2
3.
Критерий Сэвиджа
0,2
0,3
0,2
0,4
4.
Критерий Гурвица
0,1
0,4
0,4
0,3
z * z3
z * z2
z * z3
z * z1
28

29.

4. ПОКАЗАТЕЛИ И КРИТЕРИИ КАЧЕСТВА И ЭФФЕКТИВНОСТИ (ОПТИМАЛЬНОСТИ)
Математический аппарат решения задач ПУР. Классификация.
1. В условиях определенности:
1.1. Теория математического программирования, исследование операций.
1.2. Вариационное исчисление.
1.3. Теория оптимальных систем.
2. В условиях риска:
2.1. Теория вероятностей и математическая статистика.
2.2. Теория случайных процессов.
2.3. Статистическая динамика систем управления.
2.4. Адаптивные системы.
3. В условия неопределенности. Сложные системы.
3.1. Системные анализ ,теория систем.
3.2. Теория игр.
3.3. Интеллектуальные системы:
3.3.1. Многомодельные многоагентные информационные среды – МИС.
3.3.2. Экспертные системы.
3.3.3. Нейронные сети.
3.3.4. Нечеткие системы.
3.3.5. Эволюционное моделирование, генетические алгоритмы.
29

30.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.1. Элементы и структура базисной модели ПУР. Принятие управленческих решений
можно представить как процесс проектирования лучшей системы альтернатив
при решении проблем(задач) управления:
{zn* ( h, m)}
{zn* (h, m)} {arg Opt (Ф(n, z, h, Ф0 , Фm },
5.1
z Z
Ф0 , Фm - векторы показателей качества моделей ОУ и ОА. В частном случае для ИСМ (3.3)
Ф0 J 0 ( z), Фm ( J k ( z), k 1, m);
5.2
m - параметр сложности ИСМ объекта управления и объектов аналогов;
h - вектор параметров значимости (веса) показателей качества ОА;
n
- объем фактических данных на ОУ.
Условия улучшающего вмешательства в проблемные ситуации:
{zn* (h, m)}
{ z 0 } - идеальная система альтернатив
5.3
1) n , m ; 2) n , m C;3) n C , m
Система альтернатив (5.1) при определенных условиях на параметры n, h, m соответствует системе
альтернатив полученной в условиях:
*
*
*
*
1). определенности {z0 (0)} ; 2) риска {zn (m C )};3) неопределенности {z0 ( h, m)} , {zn ( h, m)}.
30

31.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
Принятие решений в задачах управления (примеры):
1. планирование (прогнозирование)
5.4
g * arg Opt (Ф( g );
g G
2. идентификация (адаптация)
*
f , f n , an* , hn* arg
*
n
(Ф(n, f (a), f (a), h, g * );
Opt
5.5
f FL , f F L , an R , h R
3. оперативное управление (регулирование)
*
un* arg Opt (Ф(n, u , g n* , f n* , f n , a* , h* ).
u U
5.6
(5.5),(5.6) –задача дуального оперативного управления с идентификацией.
(5.4)- (5.6)- задача управления с самоорганизацией - стратегическое планирование и
оперативного управления с идентификацией).
*
{zn* (m)} {n, m, g * , f * , f n , a* , h* , u *} - лучшая системы альтернатив полученная при
решении задач стратегического планирования
и оперативного управления с идентификацией.
31

32.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.2. Долгосрочное прогнозирование на основе модели жизненного цикла продукции
(текущей емкости рынка) с учетом факторов внешней среды:
y * (ti ) f (ti , a ) v0 (ti ), i 1, n,
T
V j V (a ) vaj f (t , a ) dt vaj , j 1, l.
t0
5.7
Основные этапы процесса принятия решений при идентификации жизненного
цикла продукции (текущей емкости рынка) (пример):
1.
2.
Формирование исходных данных и дополнительных априорных сведений, выбор модели жизненного
цикла f k из банка моделей f1 , f 2 ,..., f m .
Формирование (выбор) комбинированного показателя качества
n
l
Ф(a, h, n) ( J 0 (a) ( y (ti ) f k (ti , a)) h j (V j V (a)) 2 ).
*
3.
2
t 1
Решение оптимизационных задач
an* (h) arg Opt (Ф(a, h, n),
a R
5.9
j 1
hn* arg Opt ( J 0 (an* (h)).
h R
4. Вычисление прогнозных значений реализованной продукции
ошибки прогноза
*
( )
5.8
y (tn1 ) y (tn1 )
y (tn1 )
*
5. Возврат, при необходимости, к пунктам 3,2,1.
5.10
y (tn1 ) на время и определение
eps, n1 n.
5.11
32

33.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.3. Атрибуты интегрированных систем управления и принятия решений в
условиях риска и неопределенности.
Системные основы:
1. Открытость.
2. Взаимодействие.
3. Идентификация (адаптация) систем в условиях неопределенности.
Уровни качества:
1. Устойчивость.
2. Помехоустойчивость.
3. Управляемость.
4. Способность (потенциальная эффективность).
5. Самоорганизация (интеграция всей имеющейся информации, стратегическое и оперативное
управление, идентификация (адаптация), принятие решений в условиях неопределенности).
Интеллектуальные технологии управления и математический аппарат:
1. Модельная основа - Многомодельные (многоагентные) информационные среды - МИС и
интегрированные системы моделей ОУ и ОА - ИСМ.
2. Многокритериальные задачи проектирования лучшей системы альтернатив с
использованием методов теории вероятностей, математической статистики, оптимизации,
имитационного моделирования.
Процесс принятия решений рассматривается в единстве с процессом управления и
! направлен
на повышения качества и эффективности систем управления.
33

34.

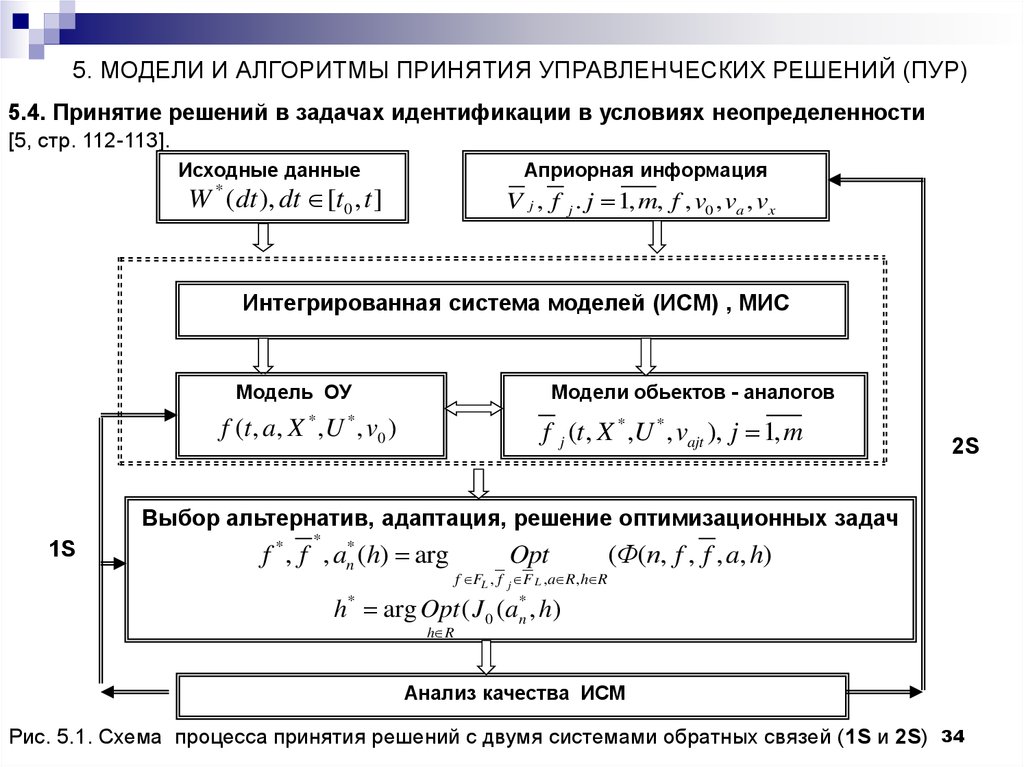
5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.4. Принятие решений в задачах идентификации в условиях неопределенности
[5, стр. 112-113].
Исходные данные
Априорная информация
W (dt ), dt [t0 , t ]
*
V j , f j . j 1, m, f , v0 , va , vx
Интегрированная система моделей (ИСМ) , МИС
Модель ОУ
Модели обьектов - аналогов
f j (t , X * ,U * , vajt ), j 1, m
f (t , a, X * , U * , v0 )
2S
Выбор альтернатив, адаптация, решение оптимизационных задач
1S
*
f * , f , an* (h) arg
Opt
(Ф(n, f , f , a, h)
f FL , f j F L , a R , h R
*
0
n
h* arg Opt ( J (a , h)
h R
Анализ качества ИСМ
Рис. 5.1. Схема процесса принятия решений с двумя системами обратных связей (1S и 2S)
34

35.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.5. Интегрированные системы моделей (ИСМ) . Классификация [ 5, стр.18-23 ].
1. Линейные ИСМ .
2. Нелинейные ИСМ.
3. Непараметрические ИСМ.
4. Комбинированные ИСМ(линейные, нелинейные, непараметрические).
1. Линейные ИСМ (пример):
m
*
yi xij a j v0i , i 1, n,
j 1
m
a j
rjk ak vaj , j , k 1, m.
k 1
Матричная форма
*
y
Fa v 0 ,
a Ra v a .
5.12
Fnm ( xij , i 1, n, j 1, m); R mm (rjk , j, k 1, m) - матрицы;
y* , a, a, v0 , va
- векторы.
Общий вид матрицы
F
(5.9) :
Fnm ( f j ( xij ), i 1, n, j 1, m), где
f j , j 1, m - функции (функционалы).
35

36.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
2. Нелинейные ИСМ (малопараметрическая система моделей добычи нефти с учетом экспертных
оценок извлекаемых запасов) [ 5, стр. 93-95]:
Q* (ti ) f (ti , a) v0i , i 1, n,
T
V j V (a) vaj f (t , a) d t vaj , j 1, l
0
Q* (ti ), i 1, n - фактические значения добычи нефти;
Матричная форма
*
Qн fн (a) v 0 ,
V V ( a ) v a ,
5.13
V j , j 1, l - экспертные оценки извлекаемых запасов.
Добыча нефти в тоннах
Q*н (Q* (ti ), i 1, n)T ;
500000
450000
400000
350000
300000
250000
200000
150000
100000
50000
0
}
V (V (a) j , j 1, l )T ;
a (a1 , a2 ,..., am )T ;
V
fн (a) ( f (ti , a), i 1, n)T ;
v 0 (v01 , v02 ,..., v0 n )T ;
1 3
5 7
9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49
Число лет разработки
Извлекаемые запасы
Фактические значения добычи нефти
Рис. 5.2
v a (va1 , va 2 ,..., van )T ;
T - символ транспонирования.
36

37.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
3. Нелинейные ИСМ (малопараметрическая система моделей добычи нефти с учетом экспертных
оценок извлекаемых запасов и прогнозных значений добычи):
Матричная форма
Q* (t ) f (t , a ) v , i 1, n,
i
i
0i
T
V j f (t , a )dt va1 j , j 1, l 1 ,
t0
Q (tn j ) f (tn j , a ) a 2 j , j 1, l 2 .
Q*н f н (a ) v 0 ,
V V (a ) v a1 ,
Q dt f dt (a) v a 2 .
Q* (ti ), i 1, n - фактические значения добычи нефти;
V j , j 1, l 1 - экспертные оценки извлекаемых запасов;
Q(tn j ), j 1, l 2 - прогнозные значения добычи нефти.
5.14
Q dt (Q í (tn j ), j 1, l 2 )T ,
fdt (a) ( f (tn j , a), j 1, l 2 )T .
Малопараметрические модели добычи нефти (примеры):
a1 exp( a2t )t a3
f (t , a)
;
a4 a5t
Модель извлекаемых запасов:
a1 exp( a2t )t a3
f (t , a)
.
a4 exp(a5t )
T
V (a ) f (t , a )dt.
t0
37

38.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.6. Показатели качества и критерии оптимальности в задачах идентификации.
Для интегрированной системы моделей
*
Y
(ti ) f (ti , a, U , X ) v0 (ti ), i 1, n,
V j f j (a, U , X ) vaj , j 1, l ,
5.15
*
процедура идентификации - проектирование (выбора) лучшей системы альтернатив {zm (l )}
заключается в решении задачи векторной оптимизации:
*
{zm* (l )} { f * , f j , an* , hn*} arg
(Ф(n, f , f , a, J 0 , h, J ).
Opt
f FL , f j F L , a Rm , h R
5.16
l
Процедура идентификации (5.16) сводится к решению задач параметрической и
структурной оптимизации :
1. определение вектора неизвестных параметров модели (5.15)
5.17
a (h, l ) arg Opt (Ф(n, f , f k , a, J 0 , hk , J k , k 1, l );
*
n
a Rm
2. определение управляющих параметров (весовых коэффициентов)
hn* arg Opt J 0 (n, an* , h);
5.18
h n Rl
3. определение оптимальной структуры модели объекта управления и объектов-аналогов
*
f * , f arg Opt (Ф(n, f , f k , an* , hn* ).
f FL , f F L
5.19
38

39.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.6. Показатели качества и критерии оптимальности в задачах идентификации.
Устранение многокритериальности в (5.17)-(5.19) осуществляется с использованием
метода свертывания векторного критерия в скалярный
m
Ф(a) J 0 (a) hk J k (a).
5.20
k 1
Частные показатели качества J 0 (a), J k (a) формируются с использованием априорной
информации о статистических характеристиках случайных величин v0 , va .
Примеры:
1. Нормальное распределение
v0 , va
2
2
J 0 (a) y f (a) , J k (a) V k f (a, Z k ) , k 1, m.
*
5.21
2. Распределение Лапласа
n
m
J 0 (a) y f (t , a,U ) , J k (a ) V kt f k (t , a, Z k ) .
t 1
*
t
5.22
k 1
39

40.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.7. Проектирование оптимальных решений в линейных системах идентификации.
Процедура проектирования (выбора) оптимальных решений в линейных системах
идентификации сводится к решению задач параметрической оптимизации [5, стр.29-35]:
l
a (h) arg min[Ф(a, h) J 0 ( a) hk J k ( a)],
*
n
a Rm
*
n
5.23
k 1
*
n
h arg min J 0 (n, a (h)),
h Rl
5.24
Задача (5.23) с использованием частных квадратичных критериев качества вида (5.21)
сводится к решению системы линейных алгебраических уравнений (СЛУ)([5, стр.30]):
*
a n (h) (F T F R T Wh R ) 1 (F T y* R T Wh a)
5.25
Wh diag (hk , k 1, m) - диагональная матрица управляющих параметров.
При Wh h I
I
решение задачи (5.24) значительно упрощается,
- единичная матрица
*
n
*
n
2
h arg min[ J 0 (n, a (h)) y f (a (h)) ].
*
n
h R1
*
5.26
40

41.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.7. Выбор оптимальных решений в линейных системах идентификации.
5.7.1. Примеры:
Матричная форма
y 1 2 ( xi xср ) v0i , i 1, n,
1 1 va1 , 2 2 va 2
*
i
*
y
Fa v0 ,
a a va
5.27
n
xср xi / n
y* , a, a, v0 , va - векторы.
i 1
Fn 2 - матрица.
Оптимальные оценки параметров([ 5, стр. 34-35 ]):
a* arg min(Ф J 0 h1 J 1 h2 J 2 ),
a
n
( h1 )
*
1
y
i 1
*
i
n
h1 1
n h1
2* (h2 )
,
( xi xср ) yi* h2 1
i 1
n
2
(
x
x
)
i ср h2
5.28
.
i 1
n
J 0 ( y 1 2 ( xi xср )) ,
i 1
*
i
2
2
J k hk ( k k ) 2
k 1
41

42.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.7. Выбор оптимальных решений в линейных системах идентификации.
5.7.2. Примеры:
yi* 1 2 ( xi xср ) v0i , i 1, n,
1 v ,
1
a1
2 2 va 2 ,
y n j 1 2 ( x n j x ср ) vaxj , j 1, m,
Матричная форма показателей
качества J 0 , J 1 , J 2 :
2
Матричная форма
y * Fa v0 ,
a a va ,
y Fa vax ,
Оптимальные оценки параметров:
2
J1 a a
2
a arg min(Ф J 0 h1k J 1k h2 k J 2 k ).
a
k 1
Оптимизационная задача (5.30) сводится к
решению системы линейных уравнений(СЛУ):
J2 y F
A a* B,
5.31
A F F W1 (h) F W2 (h)F,
(y F) W2 (h)(y F).
B F y W1 (h)a F W2 (h)y.
T
T
T
T
*
T
W2 ( h )
W1 (h) diag (h11 , h12 )
5.30
k 1
(a a)T W1 (h)(a a),
W1 ( h )
2
m
*
J 0 y Fa ,
*
5.29
W2 (h) diag (h2 j , j 1, m)
42

43.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.7. Выбор оптимальных решений в линейных системах идентификации.
5.7.1. Примеры:
Решение СЛУ (5.31)(доказательство по аналогии с 5, стр. 30):
n
1* (h1 , h 2 )
y
i 1
i
m
h11 1 h2 j y n j
j 1
m
n h11 h2 j
n
, 2* (h1 , h 2 )
y (x x
i 1
i
ср
i
(x x
i
j 1
m
) h12 2 h2 j y n j ( x n j x ср )
ср
j 1
m
) 2 h12 h2 j ( x n j x ср ) 2
. 5.32
j 1
Оптимизационная задача по определению управляющих параметров :
n
h , h arg min( J 0 (h1 , h2 ) ( yi* 1* ( h1 , h 2 ) 2* (h1 , h 2 )( xi xср )) 2 ).
*
1
*
2
h1 , h2
5.33
i 1
Упрощение оптимизационной задачи (5.33):
1. h11 h12 h1 , h2 j h2 , j 1, m,
2. h2 j h1K ( j / h2 ), j 1, m,
K ( x)
- весовая функция.
43

44.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.8. Выбор оптимальных решений в нелинейных системах идентификации
(на примере интегрированной малопараметрической системы моделей (ИСМ) добычи нефти с
учетом экспертных оценок извлекаемых запасов и прогнозных значений добычи (5.14)):
*
Q
н f н (a) v 0 ,
V V (a ) v a1 , Q dt f dt (a) v a 2 ,
Q*í (Q* (ti ), i 1, n) -
V (V j , j 1, l1 ) -
5.34
вектор фактические значения добычи нефти;
вектор экспертные оценки извлекаемых запасов;
Qdt (Q(tn j ), j 1, l 2 ) - вектор прогнозные значения добычи нефти.
Процедура проектирования ( выбора) оптимальных решений в нелинейной ИСМ (5.34)
сводится к решению задач параметрической и структурной оптимизации [5, стр. 27-28]:
l1
l2
a (h1 , h2 ) arg min[Ф( f , a, h) J 0 (a) h1k J 1k (a) h2 k J 2k (a)],
*
n
a Rm
k 1
*
5.35
k 1
*
n
h arg min J 0 ( f , a (h)), h h1 h2 ,
5.36
h
*
f * arg Opt (Ф( f , an* (h )).
5.37
f FL
FL ( f1 , f2 , ..., fm ) - множество альтернативных моделей добычи нефти.
44

45.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.8. Выбор оптимальных решений в нелинейных системах идентификации
(на примере ИСМ добычи нефти с учетом экспертных оценок извлекаемых запасов и прогнозных
значений добычи (5.34)).
Задача параметрической оптимизации (5.35) при использовании частных квадратичных
показателей качества и метода Гаусса- Ньютона сводится к последовательному решению
СЛУ [ 5, стр. 44-46,93-99] :
i
i 1
i 1
a
a
r
a
, i 1, 2,3,...,
i
5.38
i 1 i 1
i 1
A
a
B
,
T
Ai 1 (DT D D W1 (h1 )D DTpW2 (h2 )D p )i 1; B
D (
f (ti , a)
, i 1, n, j 1, m);
a j
V (a)
D (
j 1, m)T ;
a j
Dp (
i 1
T
(D T e D W1 (h1 )e DTpW2 (h 2 )e p )i 1;
f (tn k , a)
, k 1, l 2 , j 1, m) - матрицы;
a j
e (Q*í fí (a)); e p (V V (a))
- векторы;
W1 (h1 ) (diag (h1k , k 1, l1 )); W2 (h2 ) (diag (h2k , k 1, l 2 )) - диагональные матрицы управляющих
параметров
h1 , h 2 .
45

46.

5. МОДЕЛИ И АЛГОРИТМЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ (ПУР)
5.8. Выбор оптимальных решений в нелинейных системах идентификации
(на примере ИСМ добычи нефти с учетом экспертных оценок извлекаемых запасов и прогнозных
значений добычи (5.35)).
Варианты упрощения задачи (5.36) по определению управляющих параметров:
1. В ИСМ добычи нефти (5.34) использовать усредненную экспертную оценку
извлекаемых запасов, например:
l2
V
1
V k.
l2 k 1
5.39
2. В силу убывающей достоверности прогнозных значений добычи нефти Q(tn j ) (5.34),
размерность вектора управляющих параметров h2 (h2 k , k 1, l 2 ) можно сократить
используя функцию K ( x):
5.40
h h K ( j / h ), j 1, l ,
2j
1
2
2
( K ( x) e x ) пример весовой функции.
2
Результат допущений (5.39),(5.40) :
Сокращение размерности вектора управляющих параметров с l1 l2 до трех
*
*
h (h1 , h2 , h3 )
h arg min J 0 ( f , a (h )),
5.41
h
Для решения оптимизационной задачи (5.41) целесообразно использовать методы
оптимизации без вычисления производных (метод деления отрезка пополам, метод
деформированного многогранника [12 ] и т.п.)
46

47.

6. СИСТЕМЫ ПОДДЕРЖКИ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
6.1. Проектирование систем поддержки принятие решений. Основные этапы проекта:
1.Техническое задание (ТЗ) (содержит: 1) цели и задачи проекта; 2) модели, алгоритмы и
программные средства,3) требование к комплексу программ; 4) содержание пояснительной
записки;5) исходные данные для тестовых примеров; 6) список литературы.
ТЗ предоставляется заказчиком (руководителем проекта) на основе которого осуществляется
проектирование и реализация системы.
2. Разработка комплекса алгоритмов и программ (включает: 1) модели и алгоритмы
необходимые для достижения целей и решения поставленных задач; 2) используемые и
разработанные программные продукты; 3) обоснование целесообразности использования
предлагаемых моделей, алгоритмов и программных средств. Показатели качества и
эффективности.
3. Тестирование программ, определение потенциальной эффективности моделей,
алгоритмов управления и принятия решений ( включает: 1) примеры решения
предложенных в ТЗ тестовых задач; 2) примеры, демонстрирующие работоспособность, качество
и эффективность моделей, алгоритмов и программ.
4. Пояснительная записка к проекту (оформляется в соответствии с требованиями ТЗ).
5. Защита проекта и его этапов (защита этапов проекта производится согласно планyграфикy работ).
47

48.

6. СИСТЕМЫ ПОДДЕРЖКИ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
6.1. Проектирование систем поддержки принятия решений
Проекты по теме
« Системы мониторинга и прогноза промыслово-технологических показателей
(ТПР ) объектов разработки месторождений углеводородов»:
1. Формирование базы данных технологических показателей объектов разработки
нефтяных месторождений.
2. Прогнозирование ТПР (добычи флюидов, извлекаемых запасов и коэффициента
извлечения нефти - КИН) с учетом априорной информации:
2.1. Долгосрочное прогнозирование ТПР с использованием малопараметрических
промыслово - технологических моделей и экспертных оценок.
2.1.1. Прогнозирование ТПР на основе малопараметрических моделей добычи нефти.
2.1.2. Прогнозирование ТПР на основе малопараметрических моделей накопленной
добычи нефти.
2.2. Краткосрочное прогнозирование добычи нефти и оценка технологической
эффективности геолого - технических мероприятий (ГТМ);
2.2.1. Прогнозирование добычи нефти и оценка эффективности ГТМ на основе
характеристик обводнения и экспертных оценок.
2.2.2. Прогнозирование добычи нефти и оценка эффективности ГТМ на основе моделей
фильтрации флюидов и экспертных оценок.
48

49.

6. СИСТЕМЫ ПОДДЕРЖКИ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
6.1. Проектирование систем поддержки принятия решений
Проекты по теме
«Системы идентификации параметров залежей углеводородов по результатам
гидродинамических исследований скважин (ГДИС):
1. Идентификация параметров нефтяных и газовых залежей углеводородов по
результатам ГДИС с учетом априорной информации:
1.1. Метод интегрированных моделей кривой восстановления давления (КВД).
1.2. Метод детерминированных моментов.
1.3. Метод касательных.
1.4. Метод интегрированных моделей индикаторной кривой (ИК).
1.5. Метод интегрированных моделей комбинированных ГДИС(ИК и КВД).
2. Адаптивная идентификация параметров нефтяных и газовых залежей в процессе
ГДИС с учетом априорной информации :
2.1. Адаптивный метод интегрированных моделей КВД.
2.2. Адаптивный метод детерминированных моментов.
2.3. Адаптивный метод касательных.
2.4. Адаптивный метод идентификация параметров пластов в процессе нормальной
эксплуатации скважин (без их остановки) с использованием промысловотехнологических моделей и экспертных оценок.
49

50.

6. СИСТЕМЫ ПОДДЕРЖКИ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ
6.1. Проектирование систем принятия управленческих решений
Проекты по темам
1. Информационная система менеджмента обучающейся организации:
1.1. Подсистема «Принятие управленческих решений».
1.2. Подсистема «Системный анализ в управлении и менеджменте» .
1.3. Подсистема «Управление знаниями» .
2. Информационная система прогнозирование показателей деятельности
фирмы (ПДФ) с учетом экспертных оценок:
2.1. Подсистема долгосрочного прогнозирования ПДФ на основе моделей жизненного
цикла продукции c учетом экспертных.
2.2. Подсистема долгосрочного прогнозирования ПДФ на основе текущей емкости
рынка экспертных оценок.
2.3. Подсистема краткосрочное прогнозирования ПДФ с учетом экспертных оценок и
оценка эффективности мероприятий по стимулированию спроса.
3. Информационная система прогнозирование ПДФ и планирования затрат на
основе моделей производственных функций с учетом экспертных оценок.
50

51.

Литература
Основная
1. Осипов Ю.М. Основы менеджмента. Учебное пособие – Томск: Томский
межвузовский центр дистанционного образования, 2001. - 144 стр. (электронный
вариант).
2. Гончаров В.И. Основы менеджмента. ООО «Современная школа», 2006.-281с.
( электронный вариант глав 5,6,8,9,10,11).
3. Акимова Т.А. Теория организации. Учебное пособие.- М.ЮНИТИ-ДАНА,2003.-367 с.
4. Литвак Б.Г. Разработка управленческого решения. Учебник. М.: ДЕЛО, 2006.- 440 с.
5. Сергеев В.Л. Адаптивные системы идентификации. Учебное пособие. – Томск:
Томск. ун-т систем упр. и радиоэлектроники, 2007. -236 с. (библиотека ТУСУРа).
51

52.

Литература
Дополнительная
6. Балдин К.В., Воробьев С.Н., Уткин В.Т. Управленческие решения. Учебник- 2-е изд.М.: Издательско - торговая корпорация. «Дашков и Кo», 2006.- 496 с.
7. Фатхутдинов р.А. Управленческие решения. Учебник. 5-е изд., перераб. и доп. – М.:
ИНФРА-М.-2002 .-314 с.
8. Турунтаев Л.П. Теория принятия решений. Учебное пособие - ТУСУР, 2002.- 224 с.
9. Веснин В.Р. Менеджмент. Учебник. Изд- во Проспект, 2004. – 504 с.
10. Анфилатов В. С., Емельянов А.А., Кукушкин А.А. Системный анализ в
управлении.- М.: «Финансы и статистика», 2002.-368 с.
11. Перегудов Ф.И., Тарасенко Ф.П. Введение в системный анализ. Учебник.- М.:
Высшая школа, 1989.
12. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах.М.:«Высшая школа», 2002.- 544 с. (библиотека ТУСУРа)
13. Рельян Я.Р. Аналитическая основа принятия управленческих решений. М.
«Финансы и статистика», 1989.- 206 с.
52

53.

Литература
Статьи, тезисы докладов, презентации
14. Кориков А.М., Севостьянов Д.В., Сергеев В.Л., Сергеев П.В. Адаптивные
интегрированные системы идентификации и управления. Вопросы проектирования и
развития //Электронные средства и системы управления: Труды Международной
научно–практической конференции. Часть 2. – Томск, изд-во ИОА СО РАН, 2005. – С. 58
– 61(электронный вариант).
15. Адаптивная система прогноза и стратегического планирования производственных
показателей фирмы с учетом факторов внешней среды. Научная сессия ТУСУР, 2008
г.(электронный вариант).
16. Алгоритмы идентификации жизненного цикла продукции и стратегического прогноза
с учетом экспертных оценок. Научная сессия ТУСУР, 2008 г. (электронный вариант).
17. Алгоритмы идентификации моделей текущей емкости рынка для прогноза и оценки
эффективности решений. Научная сессия ТУСУР, 2008 г. (электронный вариант).
18. Информационная обучающая система менеджмента организации. Научная сессия
ТУСУР, 2008 г. (электронный вариант).
19. Сергеев В.Л. Принятия управленческих решений. Презентация курса лекций.- Томск,
Томск. ун-т систем упр. и радиоэлектроники, 2011.
53