Диффузия водорода в металлах

1. Лекция 3

Диффузия водорода в металлах
1

2.

Много различных методов было использовано для
измерения диффузии водородных изотопов в металлах,
предоставивших информации относительно: a) химического
коэффициента диффузии D*, который описывает поток
атомов
растворенного
вещества
в
присутствии
концентрационного
градиента;
b)
коэффициента
самодиффузии D, который описывает случайное блуждание
индивидуальных атомов растворенного вещества в
отсутствии концентрационного градиента. Другими словами,
D* измеряет коллективное движение неразличимых частиц,
которое имеет место при неравновесных условиях, в то
время как D измеряет движение каждой различимой
частицы, которая происходит даже при равновесным
распределением атомов растворенного вещества..
Таким образом, необходимо делать четкое различие между
этими двумя коэффициентами диффузии.
2

3.

При конечных температурах атом растворенного
вещества будет находиться в непрерывном движении под
воздействием
колебания,
взаимодействуя
с
окружающими атомами и, в последствии, перемещаясь
от одного места до другого способом, который мог бы
быть описан только в статистических терминах.
Рассмотрим вероятность того, что атом растворенного
вещества, первоначально находящийся в положении R =
0, t = 0, находится около R в течение времени t, Gs (R,
t)dR
на поверхности сферы радиуса R. Условие
нормировки можно записать так
G R , t dR 1.
(5.1)
S
3

4.

=
Поскольку движение вызвано случайными силами, каждая
траектория для многих таких событий будет различна, но
распределение
вероятности
может,
однако,
быть
определено как математическое ожидание таких событий.
Учитывая, что частица теряет память о прошлом
положении на каждом шаге своего движения, мы можем
записывать
G S ( R , t ) G S R s , t G S s , ds
(5.2)
Принимая s, отвечающими настолько малым
приращениям R, t, и преобразовывая (5.2), мы получаем
.
GS R, t 1
2
GS s, s grad Gs R, t ds
t
2
s2 2
G s R , t .
6
(5.3)
4

5.

В изотропных
диффузии (5.3)
средах,
упрощается
форма
s 2 s 2 G s R , t ds ,
уравнения
(5.4)
s2
D
,
6
(5.5)
если D можно считать константой. Это последнее условие
хорошо удовлетворяется для t's больше, чем период, в
течение которого сохраняется память о предыдущем
,
движении. Распределение вероятности получено
как
уравнения диффузии:
G S R , t
1
4 Dt
3/ 2
e
R 2 / 4 Dt
.
(5.6)
Когда беспорядочное движение частицы может быть описано
классически, рассуждения, основанные на уравнении
Ланжевена, приводят к так называемому соотношению
Эйнштейна
5
D kTB ,
(5.7)

6.

где B, подвижность, определяемая из
BF ;
а именно, v – это коэффициент, который (5.8)
дает среднюю
скорость частицы под воздействием среднего числа скачков
под действием силы F. При использовании подвижности B,
поток частицы, вызванный средним значением движущей
силы F, может быть записан как
(5.9)
J B F ,
где - плотность частицы в единицу объема. В случае
неоднородного распределение атомов растворенного
вещества, движущая сила возникает как градиент
химического потенциала, вызывая поток
J B
grad
D grad .
(5.10)
(5.11)
6

7.

D* называется химическим коэффициентом диффузии (или
коэффициент диффузии Фика). В разбавленных регулярных
растворах, химический потенциал может быть написан как
h kT ln
(5.12)
0
и, следовательно
,
,
D kTB D
0 ,
(5.13)
то есть, химический коэффициент диффузии приближается к
коэффициенту самодиффузии, по меньшей мере, при низких
концентрациях водорода.
В реальных системах, всегда существуют некоторые
корреляции между атомными скачками, и в выражения,
приведенные выше, должны быть внесены для этого случая
соответствующие
изменения,
учитывающие
такую
7
корреляцию в движении атомов.

8.

В диффузии (коррелированной), геометрическая корреляция
существует между последовательными скачками: атом, который
только что перешел, имеет большую вероятность обратного
перехода, чем переход к другим возможным местам
локализации. Этот результат учитывается введением
коэффициента корреляции f1(0 < f1 < 1) в (5.5).
s2
D ft
.
6
(5.14)
Коэффициент корреляции f1 приближается к единице в
низкоконцентрированных твердых растворах внедрения.
В
химической
диффузии,
корреляция
в
движении
неразличимых частиц описана в терминах корреляционного
коэффициента подвижности fM так что
J f M B F .
(5.15)
Таким образом, fM описывает вклад в полный поток J, когда
последующие скачки вызывают перестройку близлежащих
атомов.
8

9.

Химический коэффициент диффузии теперь становится равным
D f M B
.
(5.16)
Отношение D* к D может быть написано в форме
D
1
,
D
H R kT
(5.17)
f therm
.
где HR= f1/ fM – так называемое отношение Гавани.
Отношение Гавани всегда меньше чем единица, потому что
атом, который только что перешел из-за воздействия
градиента потенциала, имеет тенденцию для скачка,
который
противодействует
увеличению
вероятности,
которую атомы имели перед этим, двигаясь вдоль
направления падения градиента, и заселяют место, которое
было
оставлено
предыдущими
атомами.
Второй
коэффициент в (5.17), известный как термодинамический
фактор ftherm, может быть рассчитан, если (5.12)
использовать для :
0
(5.18)
9
kT
0

10.

Как HR, так и ftherm оба стремятся к единице в
низкоконцентрированных твердых растворах внедрения
атомов растворенного вещества, и с учетом этого получается
значение отношения коэффициентов D*/D.
При конечных концентрациях растворенного вещества,
переходящий атом может часто попадать в определенное
положение, блокированное присутствием других атомов
растворенного вещества. Этот влияние отражает
доступностью его местоположения, и выражается множители
pv, который является вероятностью целевого местообитания,
доступного для данного атома. Тогда, среднее время
пребывания в этом состоянии, , связано со средним
временем между скачками o,
0 / pV .
(5.19)
10

11.

В простой модели блокировки одиночного нахождения, pv
для композиции x = [M] / [H] pv может быть написано как
1 x
pv 1 x / 2
1 x / 6
для
0 октапор в ГЦК,
для
Т тетрапор ГЦК
для
Т тетрапор в ОЦК
(5.20)
,
11

12.

Рис.3.1. Коэффициенты диффузии Н и С в
ванадии (V) и коэффициент самодиффузии
в ванадии
12

13.

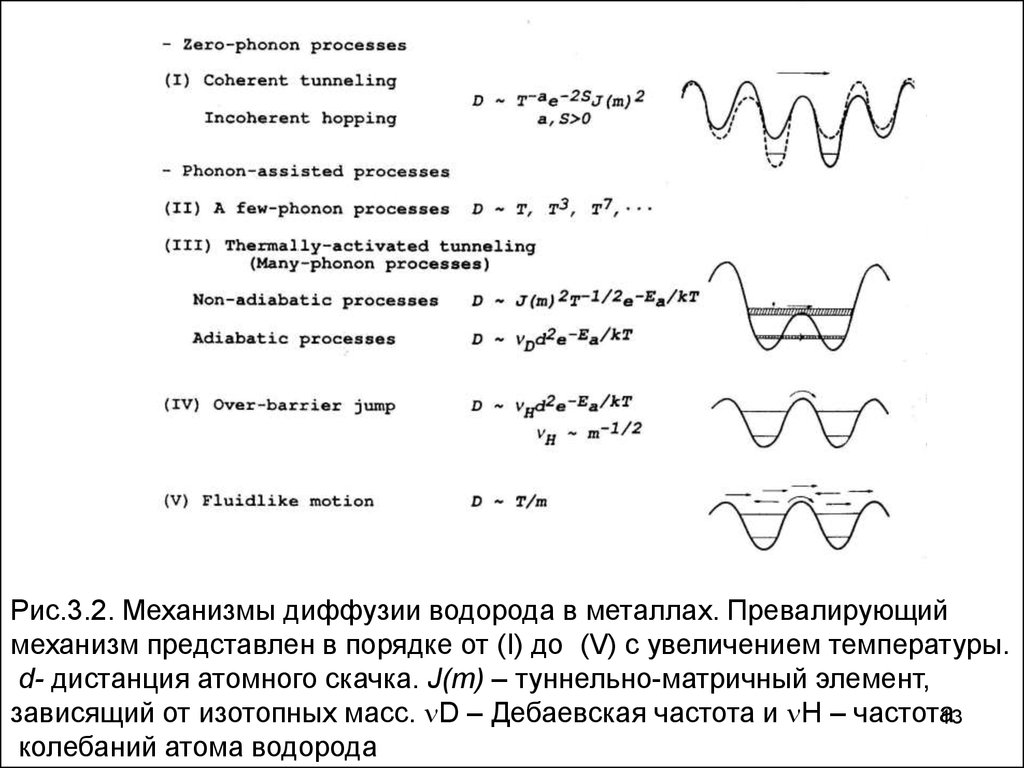
Рис.3.2. Механизмы диффузии водорода в металлах. Превалирующий
механизм представлен в порядке от (I) до (V) с увеличением температуры.
d- дистанция атомного скачка. J(m) – туннельно-матричный элемент,
зависящий от изотопных масс. D – Дебаевская частота и H – частота
13
колебаний атома водорода

14.

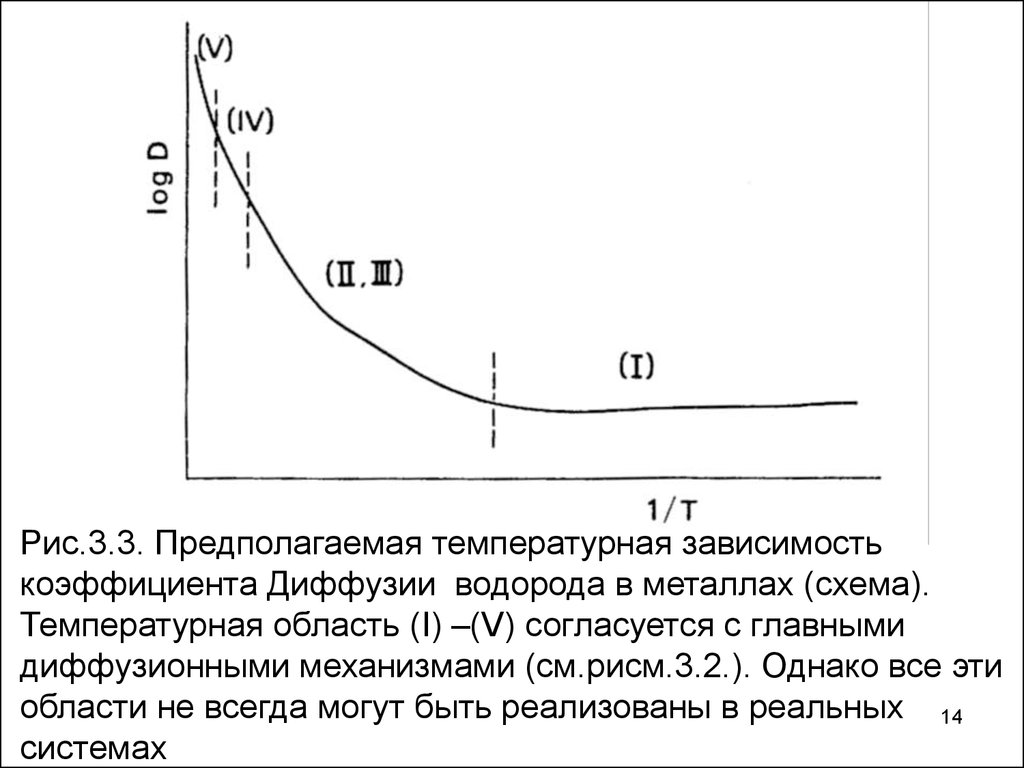
Рис.3.3. Предполагаемая температурная зависимость
коэффициента Диффузии водорода в металлах (схема).
Температурная область (I) –(V) согласуется с главными
диффузионными механизмами (см.рисм.3.2.). Однако все эти
области не всегда могут быть реализованы в реальных 14
системах

15.

Таблица 3.1.
Параметры коэффициентов диффузии изотопов водорода в некоторых
ОЦК металлах (значения Dо для D в Fe оставлены).
Металл
Изотопы
Т (К)
Dо (10-4 cm2s-1)
Ea (eV)
Fe
H
290-1040
4,2
0,040
D
273-317
4,2
0,063
H
143-667
3,1 0,8
0,045 0,004
810-1380
8,9
0,113
D
176-573
3,8 0,8
0,073 0,004
T
133-353
4,9 1,0
0,092 0,004
H
108-250
0,9 0,2
0,068 0,004
250-560
5,0 1,0
0,106 0,006
873-1390
10
0,114
D
148-560
5,2 1,0
0,127 0,006
T
159-283
4,6 1,0
0,135 0,006
H
90-190-
0,028 0,012
0,042 0,006
250-573
4,2 1,2
0,136 0,010
986-1386
10
0,167
146-573
3,8 1,2
V
Nb
Ta
D
0,152 0,00815

16.

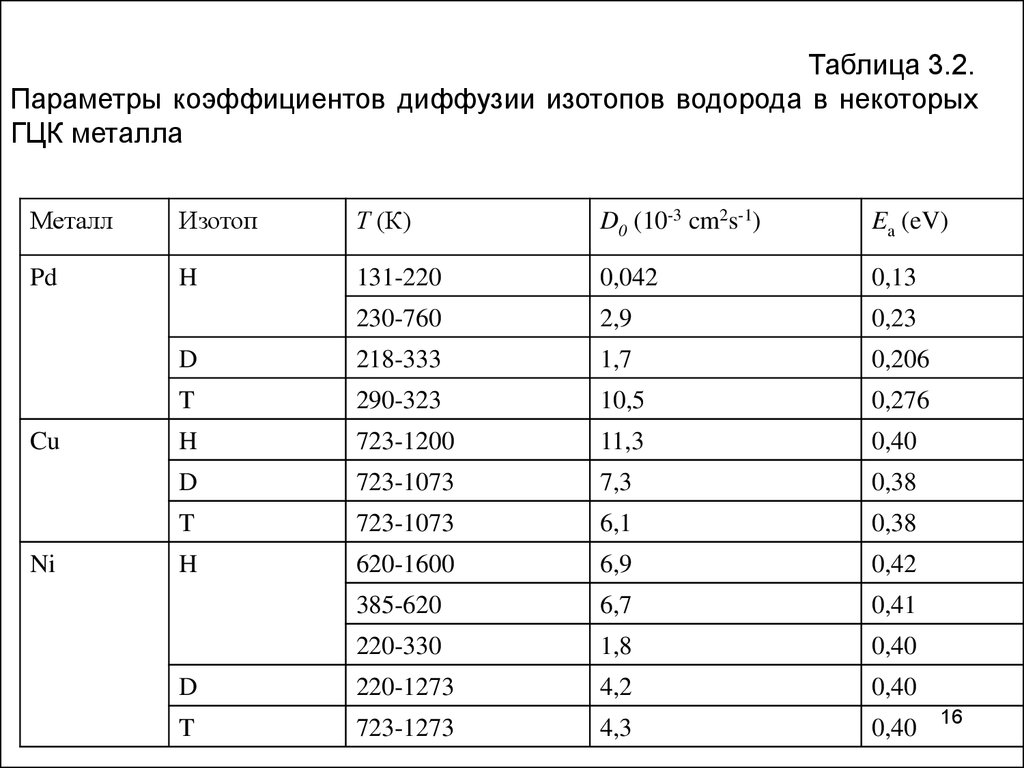
Таблица 3.2.
Параметры коэффициентов диффузии изотопов водорода в некоторых
ГЦК металла
Металл
Изотоп
Т (К)
D0 (10-3 cm2s-1)
Ea (eV)
Pd
H
131-220
0,042
0,13
230-760
2,9
0,23
D
218-333
1,7
0,206
T
290-323
10,5
0,276
H
723-1200
11,3
0,40
D
723-1073
7,3
0,38
T
723-1073
6,1
0,38
H
620-1600
6,9
0,42
385-620
6,7
0,41
220-330
1,8
0,40
D
220-1273
4,2
0,40
T
723-1273
4,3
0,40
Cu
Ni
16

17.

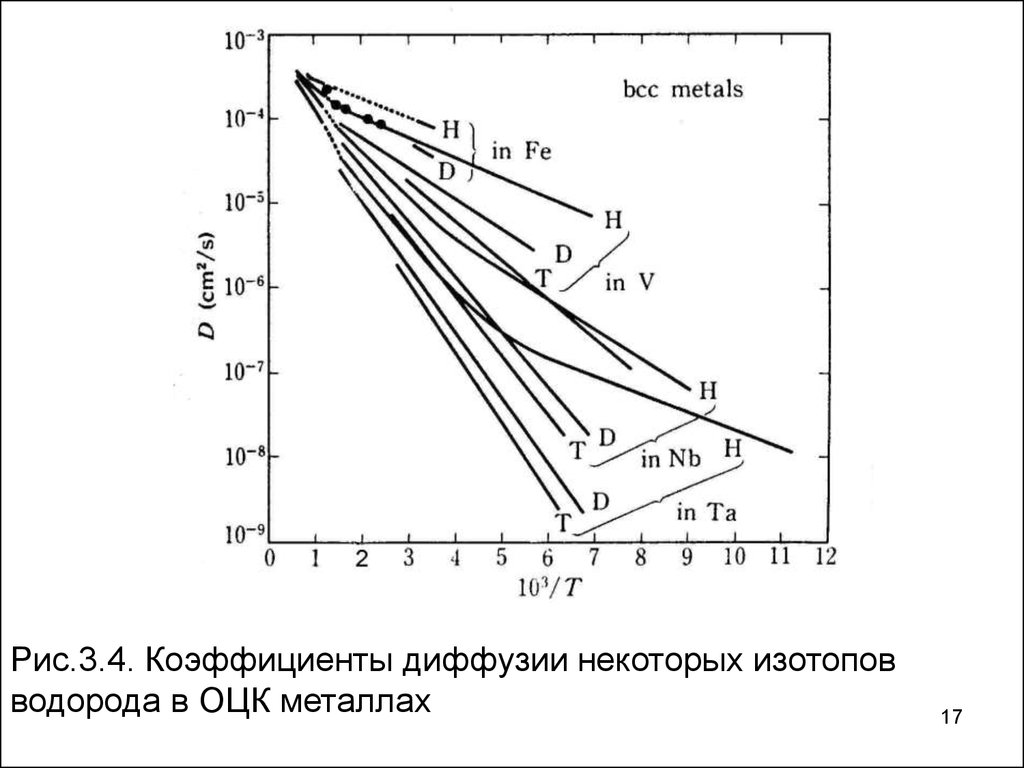
Рис.3.4. Коэффициенты диффузии некоторых изотопов
водорода в ОЦК металлах
17

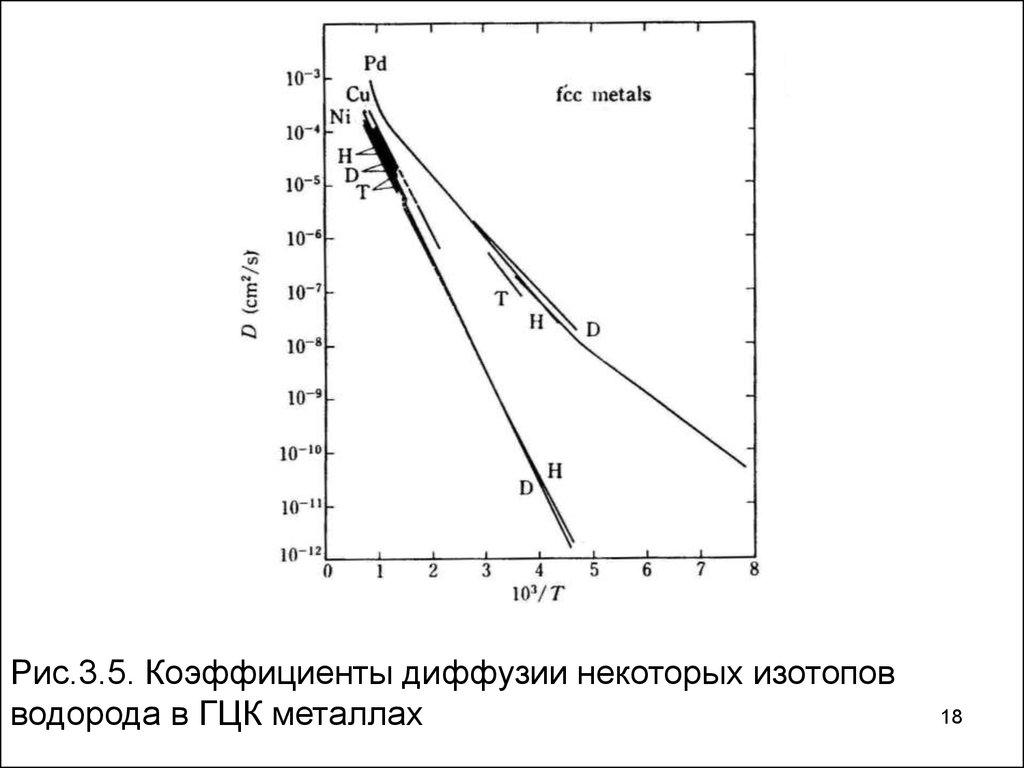
18.

Рис.3.5. Коэффициенты диффузии некоторых изотопов
водорода в ГЦК металлах
18

19.

Рис.3.6. Коэффициенты диффузии водорода в Pd0.47Cu0.53.
Диффузия много больше в ОЦК фазе (равновесной), чем в
ГЦК (закаленной) фазе
19

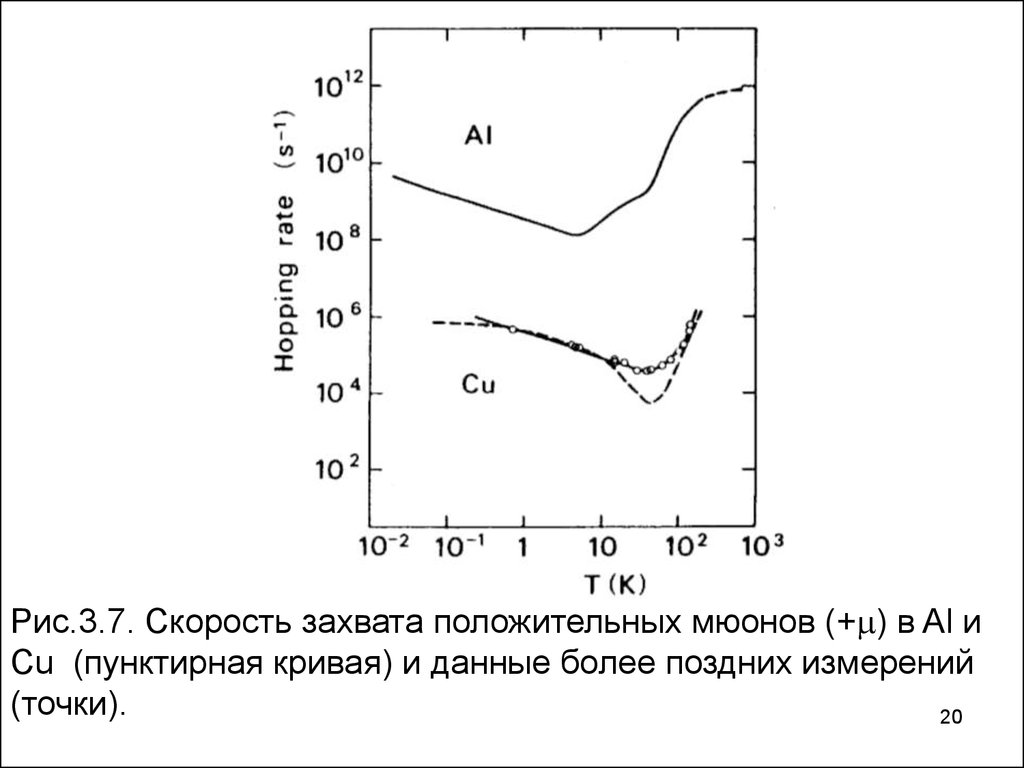
20.

Рис.3.7. Скорость захвата положительных мюонов (+ ) в Al и
Cu (пунктирная кривая) и данные более поздних измерений
(точки).
20

21.

Рис.3.8. Скорость возврата после закалки электросопротивления для Н, D
и T в Ta как функция температуры отжига. Отношение
электросопротивлений и водородная концентрация даны во вставке.
Температурная шкала для D и T смещена на 21/2 и 31/2 соответственно
21
относительно шкалы для H

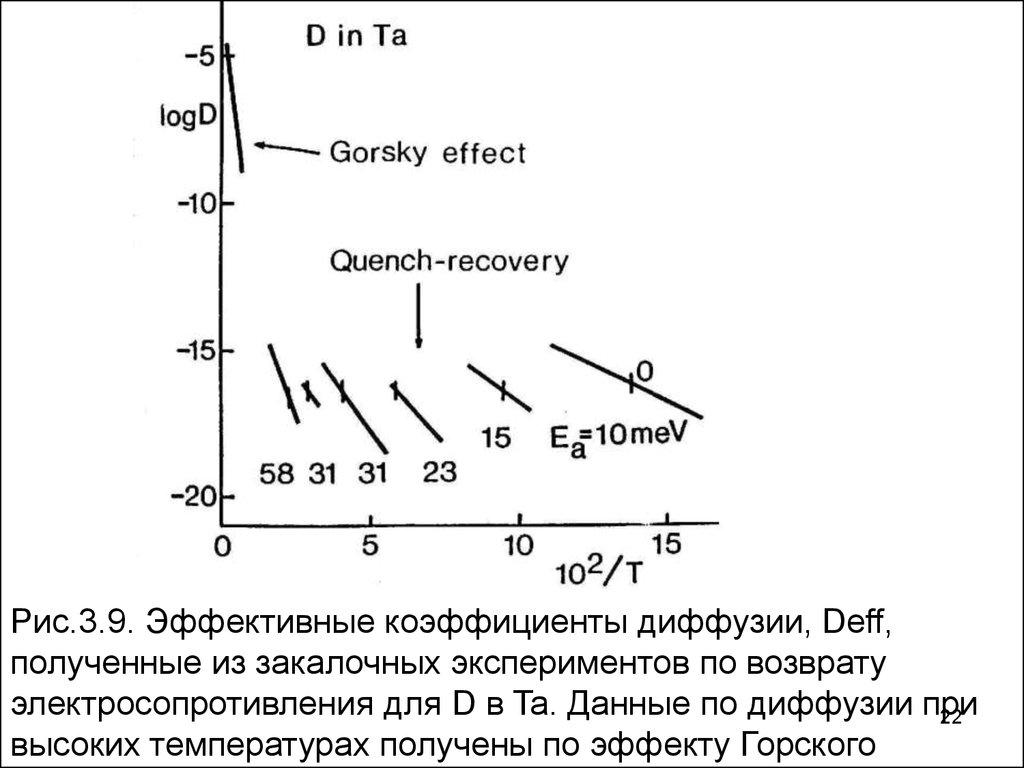
22.

Рис.3.9. Эффективные коэффициенты диффузии, Deff,
полученные из закалочных экспериментов по возврату
электросопротивления для D в Ta. Данные по диффузии при
22
высоких температурах получены по эффекту Горского

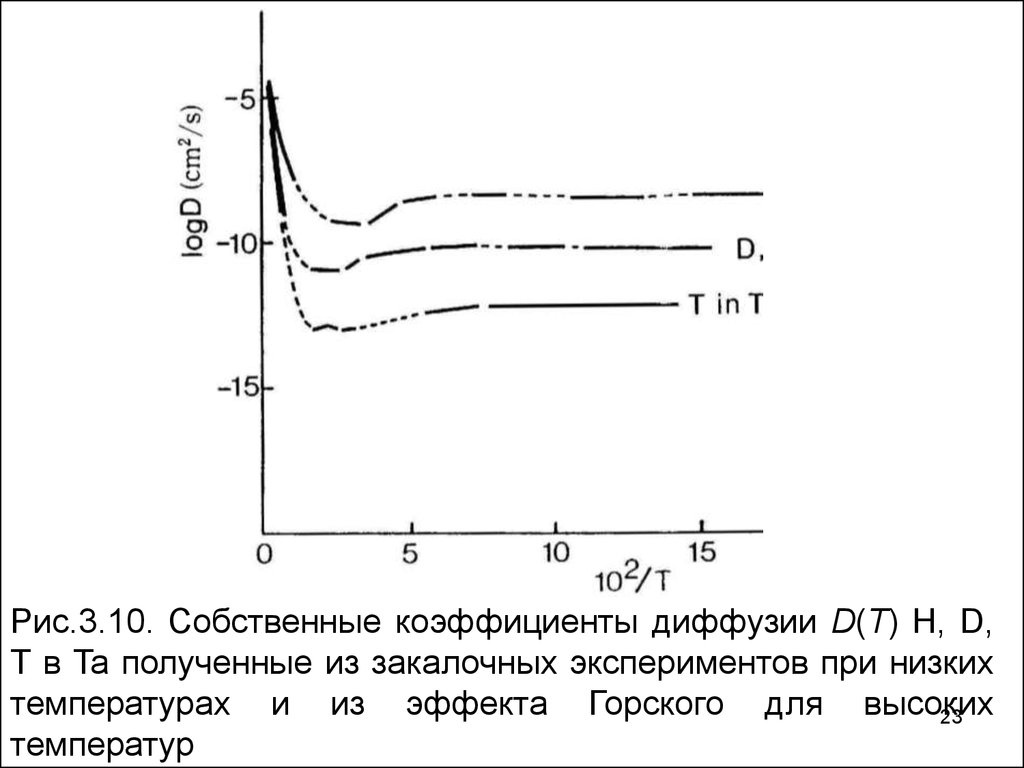
23.

Рис.3.10. Собственные коэффициенты диффузии D(T) H, D,
Т в Ta полученные из закалочных экспериментов при низких
температурах и из эффекта Горского для высоких
23
температур

24.

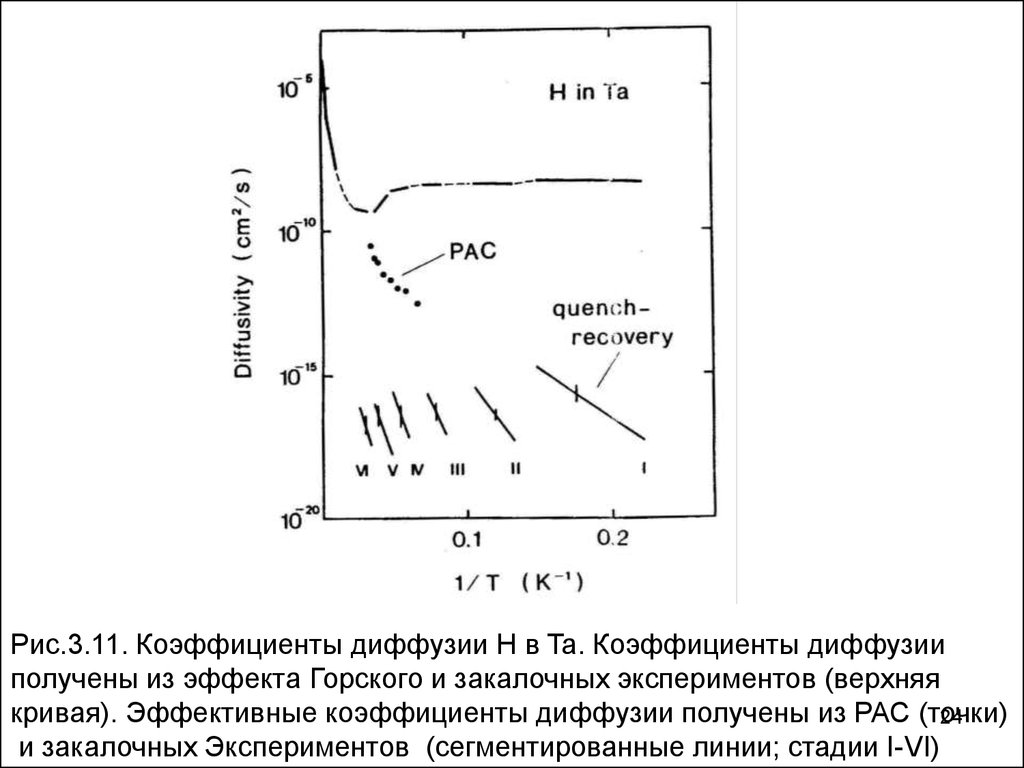
Рис.3.11. Коэффициенты диффузии Н в Ta. Коэффициенты диффузии
получены из эффекта Горского и закалочных экспериментов (верхняя
кривая). Эффективные коэффициенты диффузии получены из РАС (точки)
24
и закалочных Экспериментов (сегментированные линии; стадии I-VI)

25.

2
2
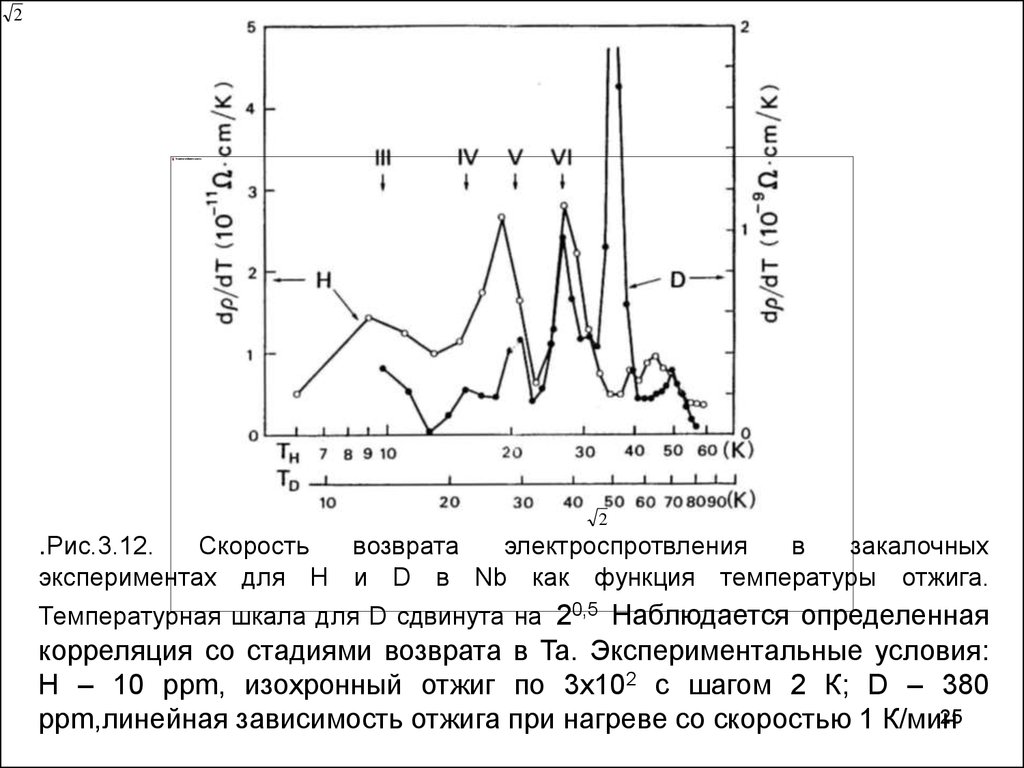
.Рис.3.12.
Скорость
возврата
электроспротвления
в
закалочных
экспериментах для H и D в Nb как функция температуры отжига.
Температурная шкала для D сдвинута на 20,5 Наблюдается определенная
корреляция со стадиями возврата в Ta. Экспериментальные условия:
Н – 10 ppm, изохронный отжиг по 3х102 с шагом 2 К; D – 380
25
ppm,линейная зависимость отжига при нагреве со скоростью 1 К/мин

26.

Рис.3.13. Гексагональная плотноупакованная решетка (сплошные
кружочки). Показана локализация Т пор (светлые кружочки). Атомы
водорода в порах А и В образуют Т-М-Т пару, тогда как водородный
атом в поре С является изолированным. Только один атом водорода
может быть размещен в непосредственной близости от пары Т пор,
таких как C и D, отделенных небольшим расстоянием ~ 1Å
26

27.

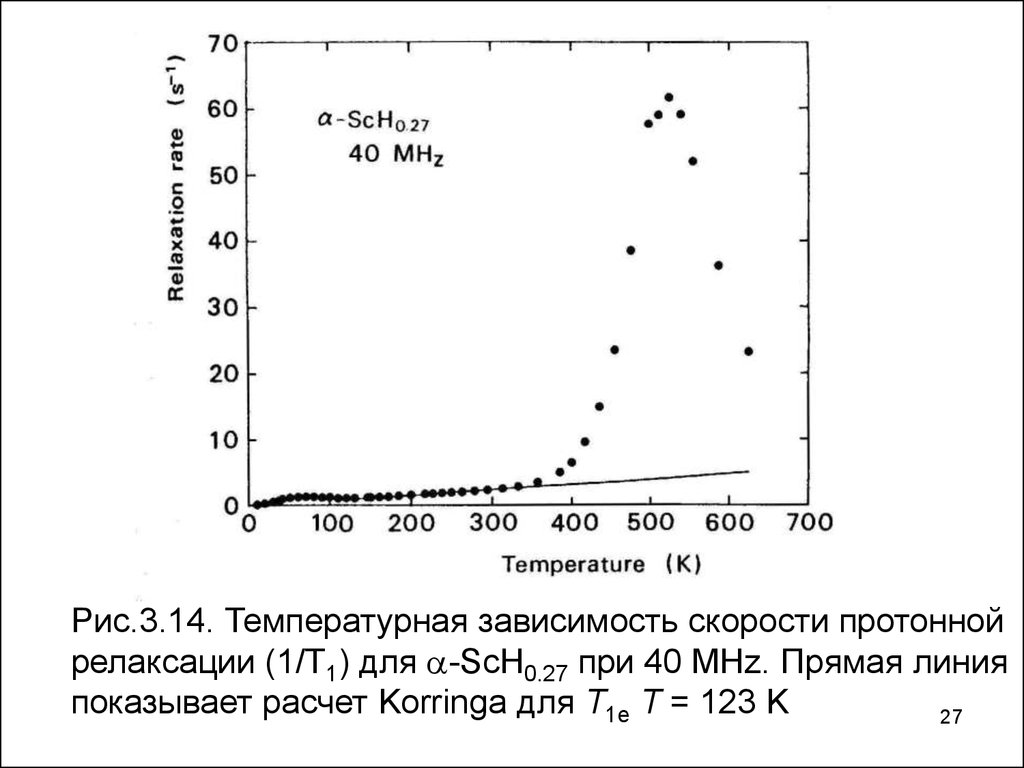
Рис.3.14. Температурная зависимость скорости протонной
релаксации (1/Т1) для -ScH0.27 при 40 MHz. Прямая линия
показывает расчет Korringa для T1e T = 123 K
27

28.

Рис.3.15. Коэффициенты диффузии водорода в V. Данные получены
абсорбционным методом ( ), при нейтронном рассеянии QNS (о) и
NMR ( ), пунктирная линия представляет экстраполяцию данных,
полученных по эффекту Горского, в область более низких температур
исходя из допущения сохранения Аррениусовской зависимости 28

29.

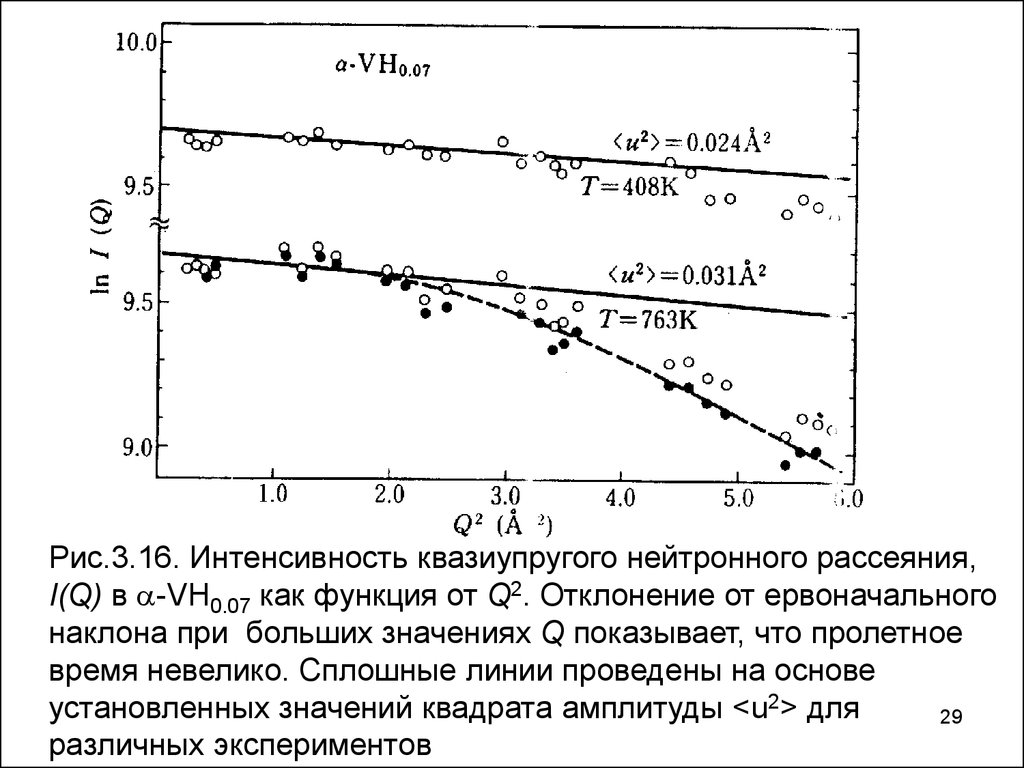
Рис.3.16. Интенсивность квазиупругого нейтронного рассеяния,
I(Q) в -VН0.07 как функция от Q2. Отклонение от ервоначального
наклона при больших значениях Q показывает, что пролетное
время невелико. Сплошные линии проведены на основе
установленных значений квадрата амплитуды <u2> для
29
различных экспериментов

30.

3.4.2. Взаимодействия между водородными атомами
При высоких концентрациях водорода поведение диффузии
изменяется из-за взаимодействия между водородными
атомами. Следовательно, все коэффициенты корреляции,
введенные в разделе 3.1.1, станут зависеть от водородных
концентраций.
Относительно направленной диффузии многочисленные
эксперименты на PdHx,: (0 < x < 1) и TiHx (1.5 < x < 2.0), где
водород локализуется в 0 и Т местонахождениях
кристаллической решетки, указывают, что концентрационная
зависимость направленного
коэффициента диффузии может быть выражена хорошей
аппроксимацией, поскольку D(x) = =pv,(x) Doe-Ea/kT, с
концентрационно-независимым Do и Ea и (5.20) для pv,(x),
основанной на блокировании одиночного местонахождения.
30

31.

Однако эксперимент на PdHx показал незначительное
отклонение от этого поведения: pv,(x) уменьшается немного
более быстро при высоких концентрациях водорода,
указывая на присутствие близкодействующего
краткосрочного отталкивания между водородными атомами.
В ОЦК металлах на направленную диффузию водорода при
высоких концентрациях влияют и более комплексные
варианты взаимодействиями между водородными атомами.
Эксперименты по водороду в V, Nb и Та с использованием
эффекта Горского, NMR и QENS показали, что и
предэкспоненциальный фактор и энергия активации
диффузии изменяются с концентрацией водорода,
D (x) = Do(x) exp [– Еа (х) / kT].
Относительно химической диффузии прежде всего
необходимо учесть очень специфическое дальнее упругое
взаимодействие. Если, ради простоты, среднее упругое
взаимодействие привести к линейной зависимости от
31
химпотенциала, т.е.

32.

/ x
x
μ h 0 ux kTln
,
r x
химический коэффициент диффузии может быть записан как
D x Bx / x B[ ux kT r ].
r x
(3.59)
Это выражение приближается к нулю, поскольку / x
имеет тенденцию стремиться к нулю около критической точки.
Это явление, известное как критическое замедление,
наблюдалось
в NbHx около критической точки спинодального распада.
Фактически
упругое
взаимодействие
настолько
дальнодействующее, что зависит от напряжений, вызванных
индивидуальными атомами водорода, которое релаксирует на
поверхности. Это случается тогда, когда напряжения
когерентно растут.
32

33.

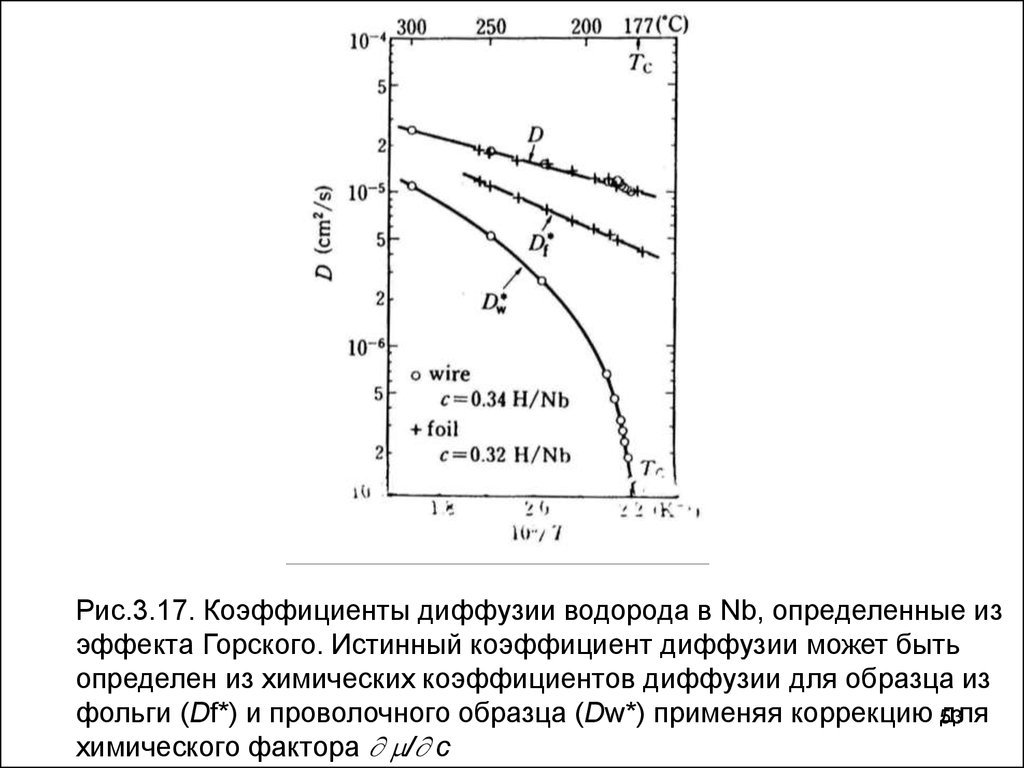
В этом случае химический потенциал и, следовательно,
химический коэффициент диффузии становятся
зависящими от формы образца, так же как и от внешних
напряжений. Зависимость от формы химического
коэффициента диффузии ясно видно на рис. 3.17, где
диффузионная способность, определенная по эффекту
Горского, в проволочных образцах и фольге существенно
различны. Эти результаты дают те же коэффициенты
направленной диффузии после того, как была сделана
коррекция для фактора / x
Теория упругого взаимодействий предлагает выражение для
коэффициентов диффузии, которые описывают затухание
распространяющихся концентрационных волн в образце для
различных мод.
Эффективный химический коэффициент диффузии для моды
j дается
(3.60)
33

34.

D j f M B
1 j ,
(3.60)
где 1 - энергия макроскопической моды, свободной от
когерентных напряжений, данная в терминах компонента
тензора стрес-дипольного взаимодействия как
ε1 Λ 2 /K 0 ,
где Ко объемный модуль.
Только когда эксперимент предназначен, чтобы измерить
концентрационный спад в состоянии когерентности (без
внутренних
напряжений),
измеренный
коэффициент
диффузии
совпадает
с
химическим
коэффициентом
диффузии. С другой стороны, в экспериментах по рассеянию
нейтронов исследуются только коротко волновые флуктуации
плотности (микроскопические или объемные моды), которые
имеют упругие энергии, отличные от 1. В упругих изотропных
средах все 1 становятся идентичным друг другу
и
34
равняются

35.

bulk 2 / c11.
(3.62)
Эффективный коэффициент диффузии, который будет
получен в этом случае, становится равным
Dbulk
D 1 1 bulk
/
1 bulk
D 1
,
f thermkT
(3.63a)
(3.63b)
при использовании термодинамического фактора при
разложении на множители, как в (3.18). Величина второго
терма в (3. 63a, b), ( 1 – buik) составляет 0.13 эВ в Nb и
0.17 эВ в Та. Это, конечно, большой вклад и требует
должного рассмотрения.
Сравнение химического коэффициента диффузии и
коэффициента самодиффузии даст полезную информацию
относительно коллективного движения атомов. Отклонение
отношения Гавани HR от единицы служит одной 35из
характеристик этого.

36.

36

37.

Отношение коэффициента D* (полученного с помощью
эффекта Горского) к D (полученному методом NMR), который
равен ftherm/ HR, было определено и совпадает со
значениями ftherm, выведенными из релаксационной силы E
в измерениях по Горскому. Полное изменение ftherm,
полученного из этих экспериментов и из данных по
растворимости, согласуется соответственно с единицей
при x=0, уменьшаясь сначала и проходя через минимум при
x=0.2 в следствии увеличении взаимодействия между
водородными атомами. Очень похожие результаты были
получены для водорода в Nb, Ta. В NbHx минимальное
значение ftherm достигает нуля вблизи критической точки
синодального распада.
37

38.

Были высказаны предположение о существовании
краткосрочных отталкивающих взаимодействиях, которые
являются непротиворечивыми с присутствием дальних
дополнительных взаимных притяжений, известных, чтобы
быть учтенными в этой области. Для 0.25 < x < 0.6
результаты непротиворечивы с блокированием кратного
местонахождения между второй и третьей
координационными сферами, имеющими тенденцию
проявляться при более высоких температурах.
38

39.

Для x>0.6 атомы значительно более мобильны, чем
предсказано третьей моделью блокировки. В целом, это
представление не противоречит термодинамическому
анализу, описанному в разделе 1.2.2. Их расчетные значения
корреляции и коэффициентов пригодности местонахождения
полезны при анализе диффузии водорода в ОЦК металлах.
В
экспериментах
по
QNS,
использующих
анализ
поляризации электромагнитной волны быстрого вращения,
произведено отдельное определение вкладов когерентных и
некогерентных рассеяний (соответственно, химического
коэффициента диффузии и самодиффузии) в одном и том
же эксперименте. Из-за уменьшения интенсивности, ~ 30 %,
анализ быстрого вращения не был достаточно корректен, но
ожидаемые
качественные
особенности
очевидны:
некогерентный пик сужается, когда Q 0.
39

40.

Принимая во внимание то, что когерентный пик
становится шире и слабее по интенсивности, когда Q 0,
были использованы различные процедуры, чтобы
определить параметры в функциях рассеяния, и найдено,
что в пределах точности эксперимента, не имелось
никакой очевидной зависимости времени скачка, по
крайней мере, не в диапазоне Q = 0.5 2.5 Å-1. При низких
Q аппроксимации были получены коэффициенты
диффузии, как D = (1.21 0.09) x l0-4 cм2 c-1 и D* = (1.0 0.4)
x 10-4 cм2 c-1 , с S (0)=0.21 0.03. Отношение Гавани тогда
становится HR = =0.77 0.44.
Рассеяние нейтронов, которое исследует флуктуацию
плотности и градиент по длинам 1 / Q 10 Å-1, как
ожидается, даст D*bulk; большие, чем истинное значение
D*, которое получается в длинноволновом приближении
(Q > 0). Для этих экспериментов на NbDx разность,
оцененная по (3.63), составляет приблизительно 20 %.40

41.

Коррелированное движение атомов водорода было
выявлено в экспериментах по смеси изотопов на NbHxDy и
TaHxDy. Пульсирующее поле в градиентном методе NMR
обеспечивает
уникальную
возможность
наблюдения
диффузии одного специфического изотопа в присутствии
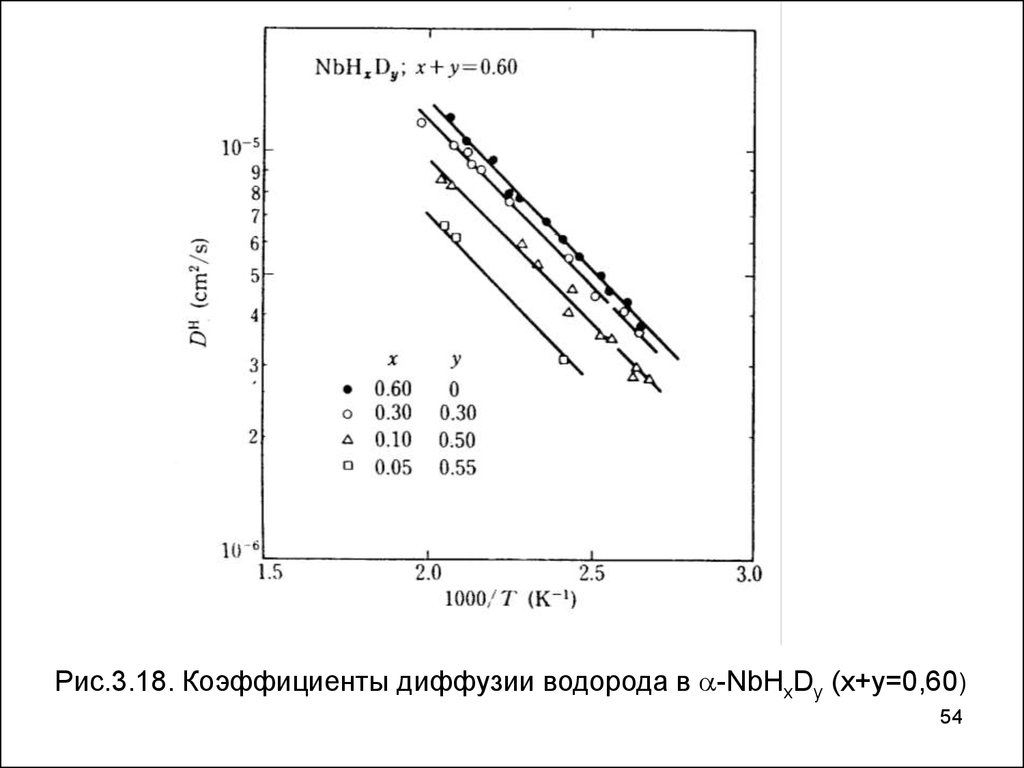
других. Результаты таких экспериментов на NbHxDy (x + у=
0.60) показаны на рис. 3.18. Коэффициент диффузии H был
измерен в образцах, имеющих ту же самую полную
концентрацию [H] + [D], но различное изотопическое
соотношение компонентов смеси. Цель этого эксперимента
состояла в том, чтобы распознать динамическую
корреляцию в диффузионном процессе. Поскольку
статическое взаимодействие между водородными атомами
может быть расценено как то же самое для обоих изотопов,
только динамическое взаимодействие, как ожидается,
обнаружится, если это вообще возможно.
41

42.

Из рис. 3.18 ясно видно, что, поскольку большее количество H
атомов заменено более медленно диффундируют D атомы и
диффузия H атомов становится медленнее. Рисунок 3.19
показывает это поведение как изменение энергии активации
Ea. (Ea была оценена, принимая Do = 2.7 x 10-4 cм2 с-1 во всех
случаях; см. табл. 3.1.) Поскольку концентрация
относительного числа H уменьшалось, Ea для H
увеличивалась и при предельно низких относительных
концентрациях, по-видимому, совпадает с Ea D атомов,
известных по измерениям эффекта Горского. Эти результаты
являются убедительным доказательство того, что движения H
атомов строго коррелированны друг с другом.
Подобное замедление диффузии присутствием более
тяжелых изотопов наблюдалось для + в NbH(D)x. Рисунок
3.19 показывает сравнение времен корреляции для + в
NbH0.92 и NbD0.92, вычисленные из скорости деполяризации
в SR, и протонов в NbD0.92, вычисленной из NMR. В
42
данном диапазоне температур образцы находятся в частично

43.

Из рис. 3.19 видно, что + - диффузия заметно медленнее в
NbD0.92, чем в NbH0.92, но энергия активации намного
ниже, чем таковая для протонов в NbD0.9. Эти
результаты демонстрируют влияние динамических
корреляций на + диффузию.
Другой аспект диффузии, который может быть связан с
высоко коррелированным движением водородных атомов,
был отмечен по времена ЯМР-релаксации при высоких
температурах. В некоторых случаях время спинрешеточной релаксации Т1, как функции температуры,
имеет второй минимум выше главного минимума,
вызванного
водородной
диффузией.
Системы,
показывающие эту высокотемпературную аномалию,
включают 1Н в дигидридах Sc, Ti, Y, Zr, и La, 2D в
дидейтеридах Sc и Y, 45Sc в ScH(D)2 и -ScH(D)x, 1Н в MHx, (М = V, Nb, Та) и 1Н в Nb0.75V0.25H0.23.
43

44.

Подобные аномалии также наблюдались в некоторых
суперионных проводниках, например 19F в PbF2. Ни в одной
из этих систем, макроскопические коэффициенты
диффузии не показывают каких-либо аномальных
изменений как функции температуры. Чтобы объяснять
эту аномальную релаксацию при высоких температурах,
необходимо искать некоторый механизм, при котором
эффективная корреляция времени, испытываемая ядрами
зонда, увеличена по сравнению со временем между
индивидуальными скачками.
Имеется достаточное основание для того, чтобы предполагать
существование некоторой формы высококоррелированного
движения водородных атомов. В простой двухъямочной
модели, где имеется доля fc водородных атомов, находящихся
в коррелированном движении и имеющими ядерную
корреляцию по временем, временная составляющая перехода
между местами расположения атомов больше, чем при
44
некоррелированном движении ( d).

45.

Эффективное время корреляции при высоких температурах
становится fc L , которое может быть намного больше, чем
d, если fc составляет большую долю общего количества
атомов.
Анализ, основанный на этой модели, привел к
заключению, что при 1250 К, L 5 d для ScH1.83 и L ~
200 d для YD1.88 , принимая fc ~ 0.5. Эти значения
кажутся весьма разумными и подтверждают эту идею.
Высокотемпературная аномалия ядерного времени
релаксации может выявить некоторые аспекты
высококоррелированного движения, которое является
едва ли доступно любыми другими средствами.
45

46.

3.5. Диффузия в неоднородных системах
3.5.1. Диффузии в кристаллических и аморфных сплавах
В системах, где кристаллическая решетка имеет те или иные
дефекты и энергия равновесного состояния и конфигурация
седловой точки для водородных атомов характеризуются
значениями,
ведущими
к
изменению
характеристик
диффузии, специфических для этих систем.
В простой двухчастичной модели водородные атомы
рассматриваются как находящиеся в свободном (подвижном)
состоянии или в связанном состоянии в течение средних
времен tf и tb соответственно. Продолжительность времени
нахождения в свободном состоянии, является равным
(пропорциональным) количеству водородных атомов в том же
самом состоянии и дается выражением
46

47.

tf
nf
1
pf
t f tb n f nb 1 nb / n f 0 e Eb / kT
(3.64)
(разд. 2.3), эффективный коэффициент диффузии Deff
Deff p f D.
(3.65)
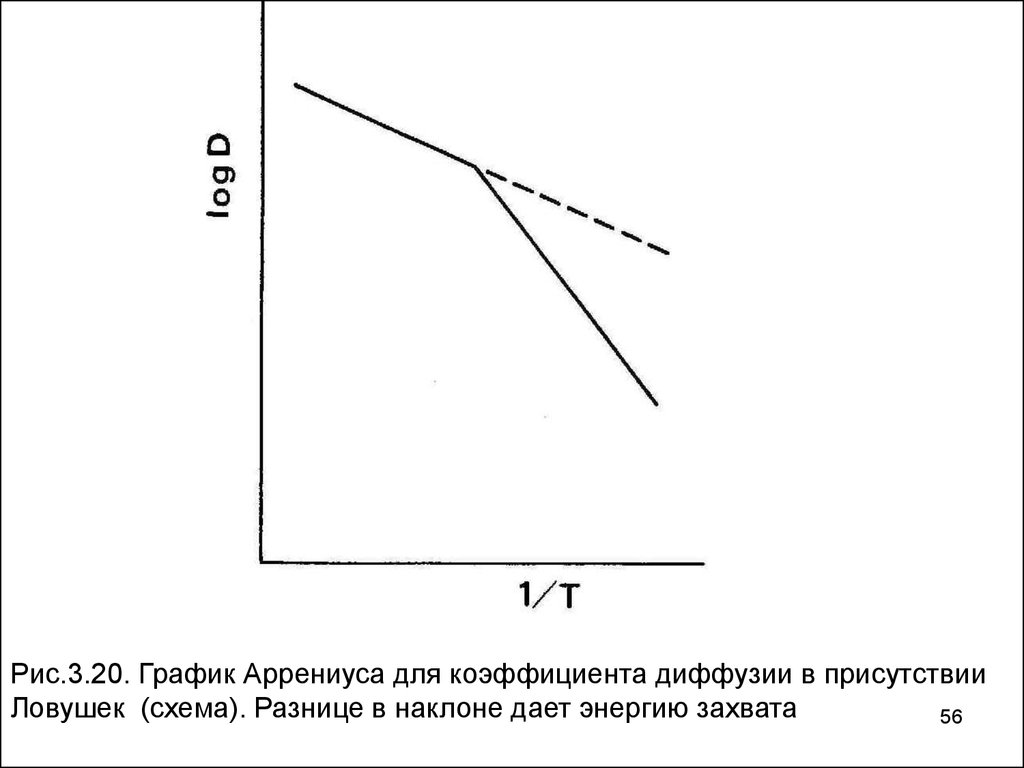
Поскольку большее количество водородных атомов
находится в ловушках при более низких температурах,
эффективный коэффициент диффузии уменьшается
относительно графика Аррениуса, как показано схематично
на рис. 3.20. Разность в наклонах при высоких и низких
температурах дает возможность определить энергию связи,
Еb. Графики Аррениуса этой формы часто наблюдаются в
металлах, имеющих низкую растворимость водорода.
47

48.

Двухчастичная модель применялась к анализу различных
экспериментов, включая эксперименты по эвакуации
водорода, описанные в разд. 3.4.2, также как NMR и QNS.
Среднее время между атомными скачками может быть
различно для свободных атомов и атомов в ловушках и
может быть обозначено как tf и tb. Оба типа атомных
скачков могут влиять на внутреннее трение, NMR и QNS.
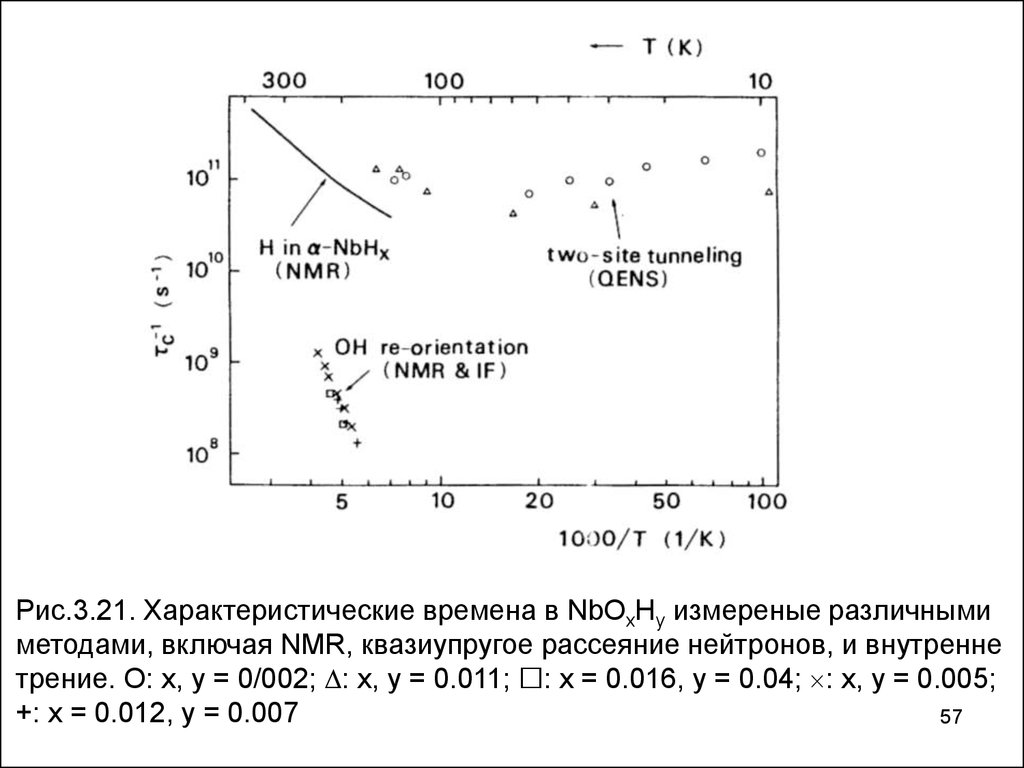
Корреляция времен, наблюдаемая в образцах NbOxHy,
показана на рис. 3.21. Продолжительность времени
корреляции, наблюдаемая при измерении внутреннего
трения и экспериментами по NMR, находятся в хорошем
соответствии друг с другом и показывают отклонение от
прямой линии, подобной тому, которое следует из
экспериментов РАС на H в Та (рис. 3.11).
48

49.

Эта корреляция времен была приписана переориентировке
водородных атомов, захваченных кислородными атомами.
С другой стороны, QNS эксперименты показали наличие
атомных скачков со средним временем намного меньшим,
чем перориентировочное движение и сопоставимое по
величине с тем, которое ответственно за диффузию при
более высоких температурах. Эти быстрые скачки,
наблюдаемые в QNS при низких температурах, были
приписаны скачкам между парой замещенных Т
местонахождений около кислородных атомов (разд. 3.4.2).
В тех случаях, когда водородные атомы занимают
структурно различные междоузлия, встречаются
корреляции, времена которых определены комбинациями
нескольких характерных времен скачков. В VHx , например,
в котором водородные атомы распределены более чем в
двух типах местонахождений (Oz1 и Oz2), по крайней мере,
четыре различных скачка должны рассматриваться (в Oz1
49
плоскостях,

50.

Oz2 плоскостях, между Oz1 Oz2, Oz2 Oz1) и двумя
различными временами корреляции, что действительно
наблюдались в ЯМР-релаксации и экспериментах по QNS
(см. разд. 3.4.1). В интерметаллидах, имеющих намного
больше типов мест нахождения для водородных атомов,
прямое распространение этого анализа не возможно и
должно быть использовано представление о непрерывном
распределении энергий старта для атомных скачков, чтобы
объяснить наблюдаемую температурную зависимость
времен релаксации. Местоположение здесь очень похоже на
то, которое наблюдается в неупорядоченных или аморфных
сплавах, где внутреннее трение и эксперименты по NMR
ясно показали расширение релаксационного пика как
функции температуры по сравнению со случаем одиночного
релаксационного процесса.
50

51.

Это расширение пика успешно объясняется тем, что
энергия активации скачков имеет распределение по
некоторому интервалу значений, составляющего обычно
0.2 0.4 от средней величины Ea.
В NMR экспериментах график Аррениуса скорости
релаксации, которая оказывается почти симметрической
пику в BPP формуле (разд. 3.2.1), становится шире и
асимметричным. Средняя величина энергии активации
может быть определена из частотной зависимости
максимальной температуры скорости релаксации, и
ширины релаксационного пика, предполагается
удовлетворительная температурная зависимость
T1 1 G Ea T1 1 Ea dEa ,
(3.66)
приняв корреляцию в виде = оехр (Еа / kT) в выражениях
BPP для T1 (или T1p).
51

52.

Подобные исследования релаксационных пиков были
выполнены для механических релаксаций, вызванных
водородом в аморфных сплавах.
В модели для водородной диффузии в неупорядоченных
системах
рассмотрено
распределение
энергий
местонахождения, но одиночное значение для энергий
седловой точки между смежными порами осталось
неизменным.
Это,
конечно,
значительно
упрощает
фактическую ситуацию, но оказалось очень полезным в
описании наблюдаемых релаксационных процессов.
Энергии седловой точки чистых V и Nb являются
производными от энергий в равновесной конфигурации и
энергии активации диффузии и близки к значениям 25.2 0.1
кДж (моль H)-1. Это наблюдалось и в сплавах Nb-V.
Постоянная энергия седловой точки была также найдена
при анализе данных по диффузии водорода в сплавах V-Ta.
52

53.

Рис.3.17. Коэффициенты диффузии водорода в Nb, определенные из
эффекта Горского. Истинный коэффициент диффузии может быть
определен из химических коэффициентов диффузии для образца из
фольги (Df*) и проволочного образца (Dw*) применяя коррекцию для
53
химического фактора / c

54.

Рис.3.18. Коэффициенты диффузии водорода в -NbHxDy (x+y=0,60)
54

55.

Рис.3.19. Время корреляции дипольного поля в экспериментах по
диффузии мюонов + в NbD0.92 ( )и NbH0.92 ( ), и H в NbH0.9 ( )
55

56.

Рис.3.20. График Аррениуса для коэффициента диффузии в присутствии
Ловушек (схема). Разнице в наклоне дает энергию захвата
56

57.

Рис.3.21. Характеристические времена в NbOxHy измереные различными
методами, включая NMR, квазиупругое рассеяние нейтронов, и внутренне
трение. O: x, y = 0/002; : x, y = 0.011; : x = 0.016, y = 0.04; : x, y = 0.005;
+: x = 0.012, y = 0.007
57

58.

Рис.3.22. Теплоемкость образцов из сверхпроводника NbOxDy с
различной концентрацией туннельных O-D комплексов
58

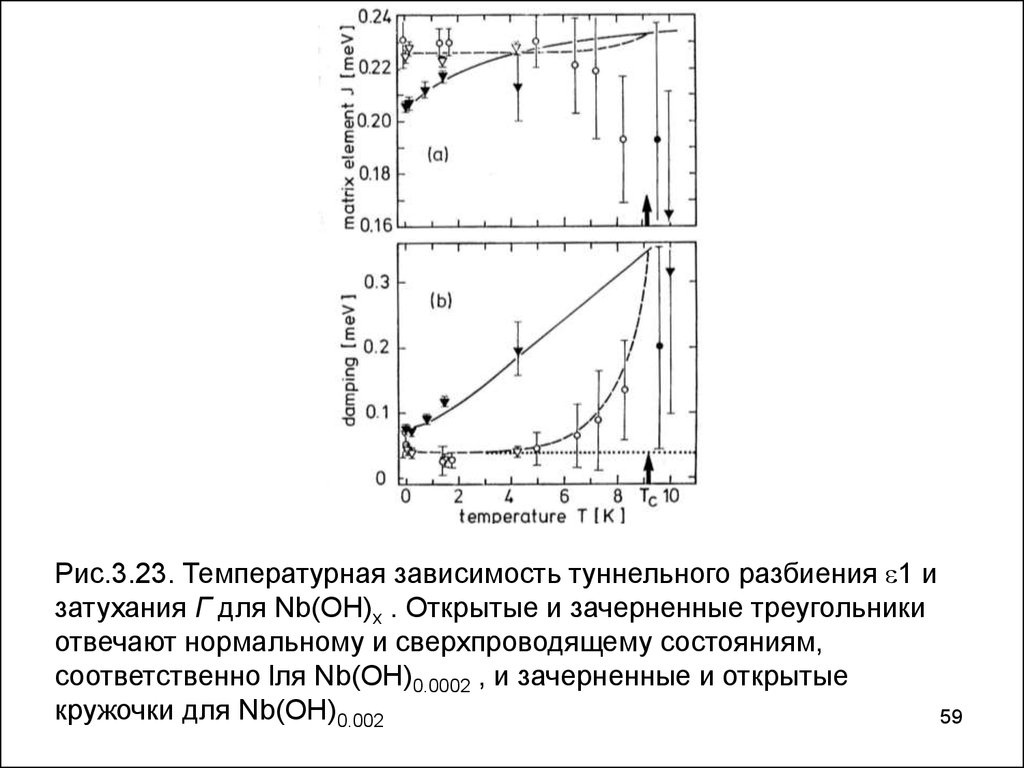
59.

Рис.3.23. Температурная зависимость туннельного разбиения 1 и
затухания Г для Nb(OH)x . Открытые и зачерненные треугольники
отвечают нормальному и сверхпроводящему состояниям,
соответственно lля Nb(OH)0.0002 , и зачерненные и открытые
кружочки для Nb(OH)0.002
59

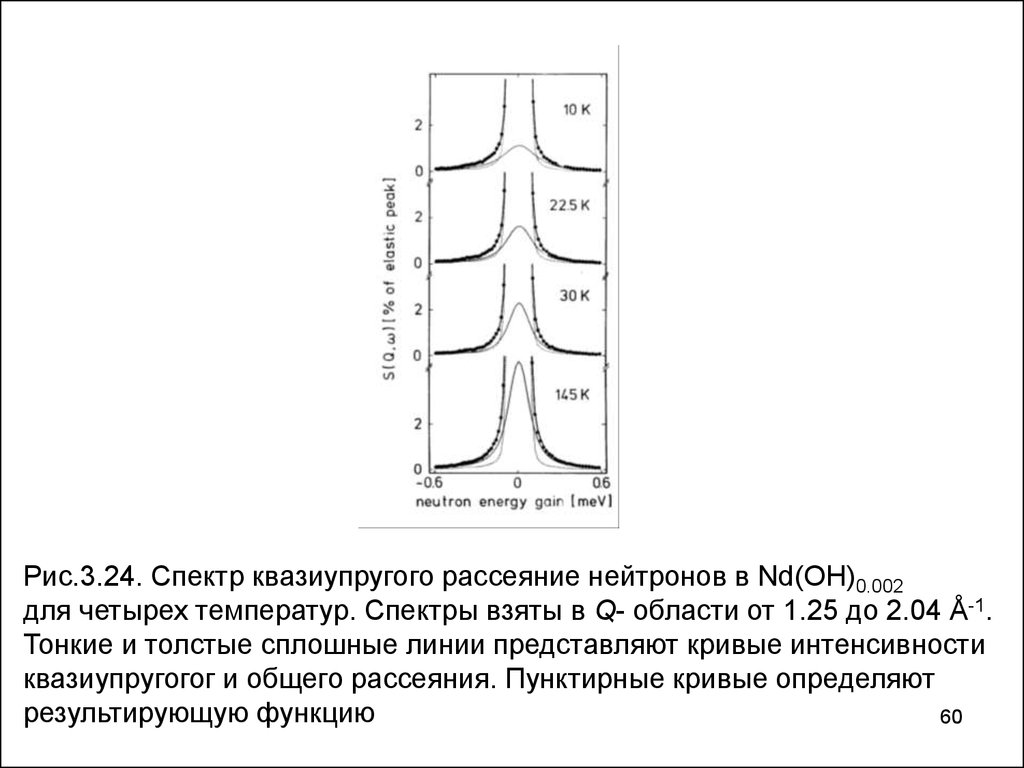
60.

Рис.3.24. Спектр квазиупругого рассеяние нейтронов в Nd(OH)0.002
для четырех температур. Спектры взяты в Q- области от 1.25 до 2.04 Å-1.
Тонкие и толстые сплошные линии представляют кривые интенсивности
квазиупругогог и общего рассеяния. Пунктирные кривые определяют
результирующую функцию
60

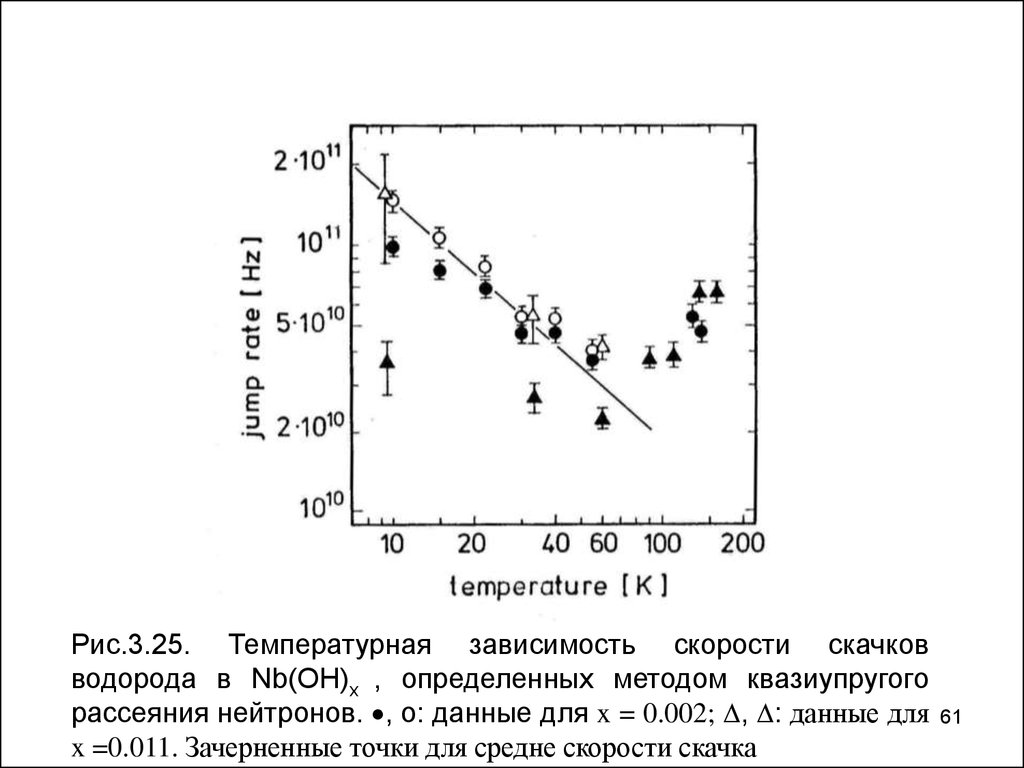
61.

Рис.3.25. Температурная зависимость скорости скачков
водорода в Nb(OH)x , определенных методом квазиупругого
рассеяния нейтронов. , о: данные для x = 0.002; , : данные для
x =0.011. Зачерненные точки для средне скорости скачка
61

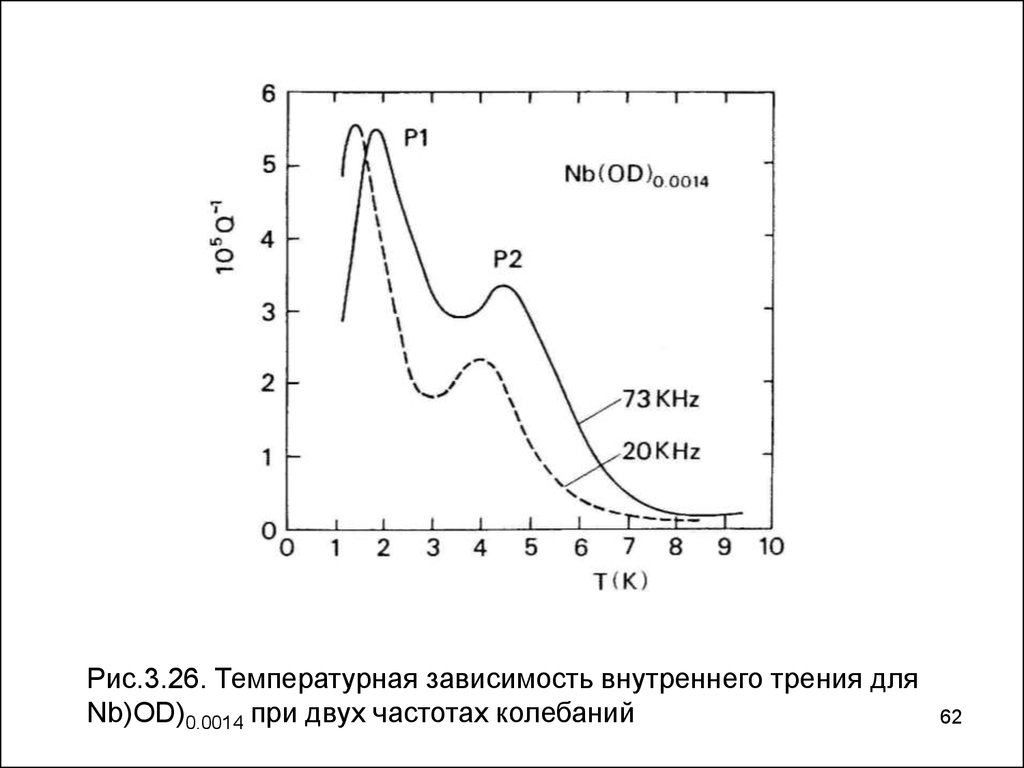
62.

Рис.3.26. Температурная зависимость внутреннего трения для
Nb)OD)0.0014 при двух частотах колебаний
62

63.

3.5.2. Движения водородных атомов около атомов
примеси
в металлах с ОЦК решеткой
Водородные
атомы,
захваченные
междоузельными
атомами (0, N,...) в ОЦК металлах, являются особенно
интересными примерами для понимания квантовой
особенности атомных скачков. Это связано с тем, что
водородные атомы, захваченные этими примесями, не
стремятся формировать гидридную фазу, но остаются
такими при низких температурах, обеспечивая особый
случай для возникновения квантовых эффектов.
Конфигурация захваченного водородного атома, как
полагают,
является
такой,
что
она
занимает
преимущественно одну из восьми эквивалентных пар
(слегка замещенный) Т местонахождения в направлении
<111> от атома примеси, и скачки переориентации между
этими эквивалентными парами наблюдаются при
63
измерениях внутреннего трения.

64.

Существование внутренних возбужденных состояний
водородных атомов в этой конфигурации, включающих очень
маленькие энергии, было сначала отмечено в измерениях
удельной теплоемкости при низких температурах.
Убедительно продемонстрировано, что аномалии удельной
теплоемкости ниже 2 К, предварительно наблюдаемые в V, Nb
и Та, были фактически связаны с присутствием небольшого
количества растворенных водородных атомов, и, на основе
сильной изотопической зависимости этих аномалий,
высказано предположение о том, что некоторое движение при
туннелировании водородных атомов могло бы быть
ответственно за это.
64

65.

Более тщательные измерения удельной теплоемкости
производились с целью выяснения природы квантовых
состояний водородных атомов. Рисунок 3.22 показывает
зависимость удельной теплоемкости от концентрации
захваченных водородных атомов. Такие зависимости могут
быть сильно нелинейными. Эти наблюдения описываются
моделью, согласно которой захваченный водородный атом
перемещается
туннелированием
между
двумя
эквивалентными
междоузлиями
(формирующими
делокализованные 2T конфигурации), чьи соответствующие
энергии произвольно смещены относительно друг друга и
должны образовать решетку дефектов, возникающих из
других комплексов (О-H, и т.д.).
65

66.

Рис.3.22. Теплоемкость образцов из сверхпроводника NbOxDy с
различной концентрацией туннельных O-D комплексов
66

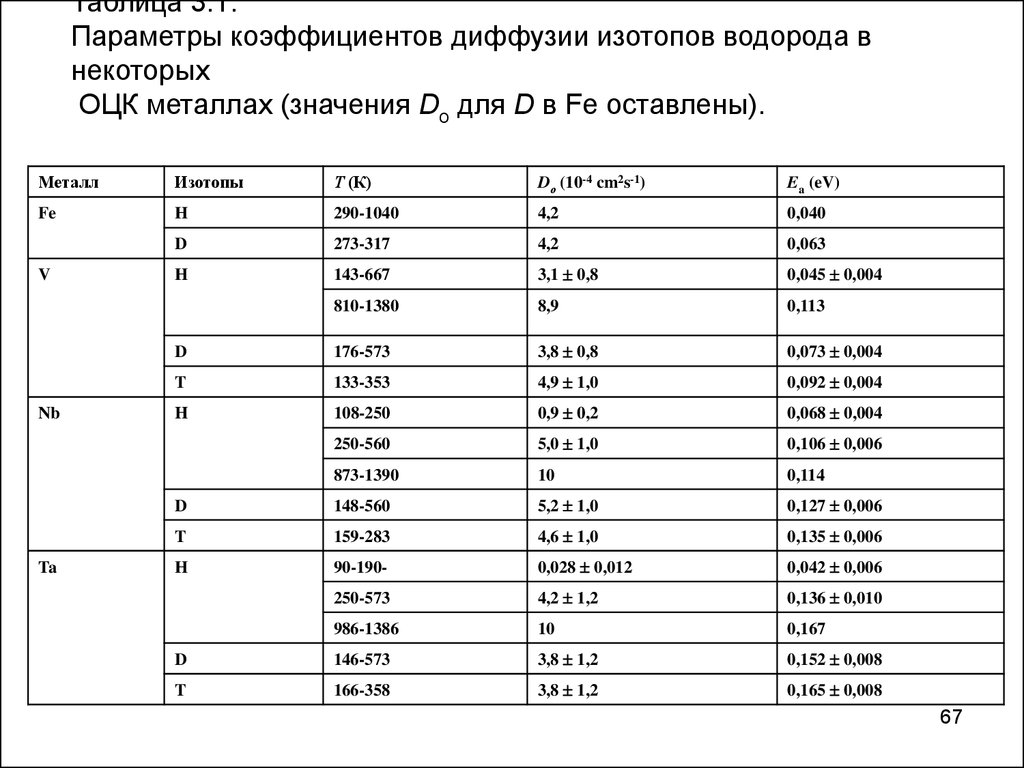
67.

Таблица 3.1.
Параметры коэффициентов диффузии изотопов водорода в
некоторых
ОЦК металлах (значения Dо для D в Fe оставлены).
Металл
Изотопы
Т (К)
Dо (10-4 cm2s-1)
Ea (eV)
Fe
H
290-1040
4,2
0,040
D
273-317
4,2
0,063
H
143-667
3,1 0,8
0,045 0,004
810-1380
8,9
0,113
D
176-573
3,8 0,8
0,073 0,004
T
133-353
4,9 1,0
0,092 0,004
H
108-250
0,9 0,2
0,068 0,004
250-560
5,0 1,0
0,106 0,006
873-1390
10
0,114
D
148-560
5,2 1,0
0,127 0,006
T
159-283
4,6 1,0
0,135 0,006
H
90-190-
0,028 0,012
0,042 0,006
250-573
4,2 1,2
0,136 0,010
986-1386
10
0,167
D
146-573
3,8 1,2
0,152 0,008
T
166-358
3,8 1,2
0,165 0,008
V
Nb
Ta
67

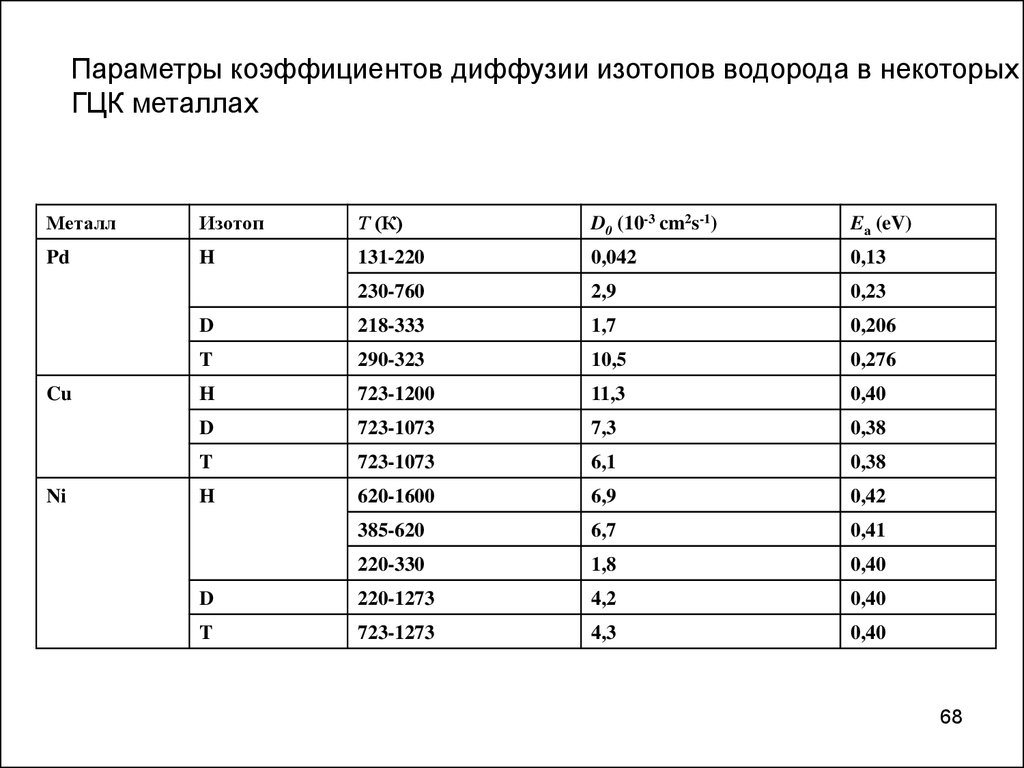
68.

Параметры коэффициентов диффузии изотопов водорода в некоторых
ГЦК металлах
Металл
Изотоп
Т (К)
D0 (10-3 cm2s-1)
Ea (eV)
Pd
H
131-220
0,042
0,13
230-760
2,9
0,23
D
218-333
1,7
0,206
T
290-323
10,5
0,276
H
723-1200
11,3
0,40
D
723-1073
7,3
0,38
T
723-1073
6,1
0,38
H
620-1600
6,9
0,42
385-620
6,7
0,41
220-330
1,8
0,40
D
220-1273
4,2
0,40
T
723-1273
4,3
0,40
Cu
Ni
68

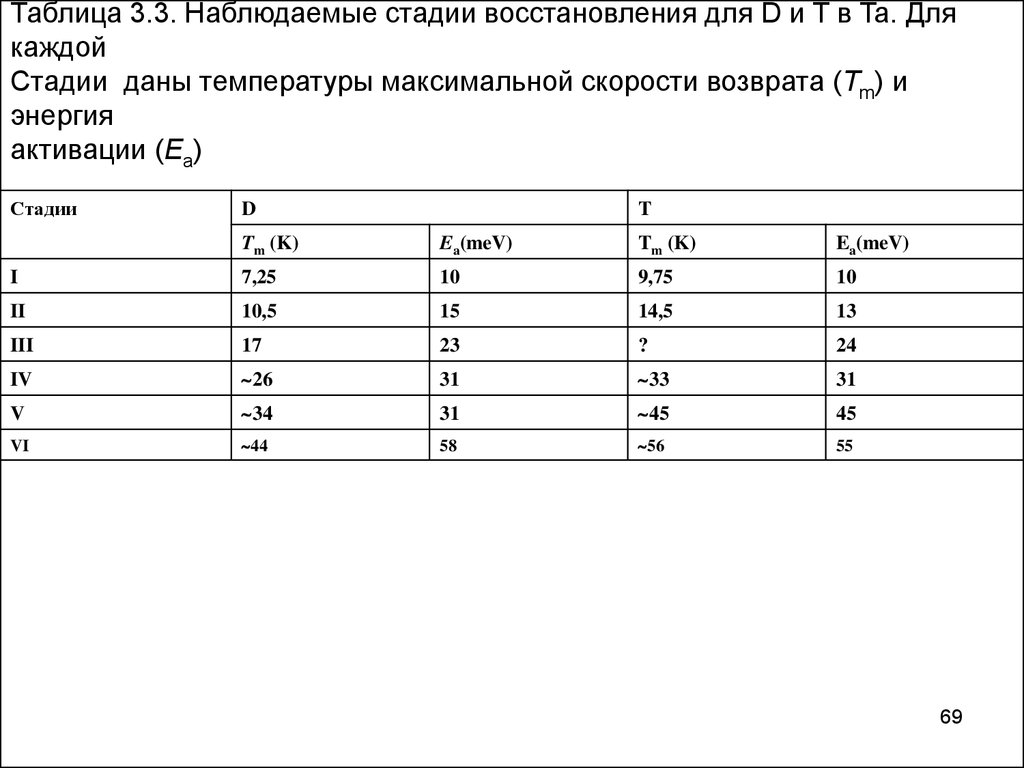
69.

Таблица 3.3. Наблюдаемые стадии восстановления для D и T в Ta. Для
каждой
Стадии даны температуры максимальной скорости возврата (Tm) и
энергия
активации (Ea)
Стадии
D
T
Tm (K)
Ea(meV)
Tm (K)
Ea(meV)
I
7,25
10
9,75
10
II
10,5
15
14,5
13
III
17
23
?
24
IV
26
31
33
31
V
34
31
45
45
VI
44
58
56
55
69

70.

Таблица 3.4. Температурная зависимость параметров моделей
3 и 4. р1 - вероятность скачка в ближайшую Т-пору. p2 –
вероятност
ь двойного скачка, m - среднее время нахождения в процессе
движения
и r - среднее время в покое
Т (К)
Модель 3
Модель 4
р2/р1
mp1
m/( m + r)
293
0
3,2
0,64
431
0,4
5,5
0,66
581
1,4
6,0
0,64
70

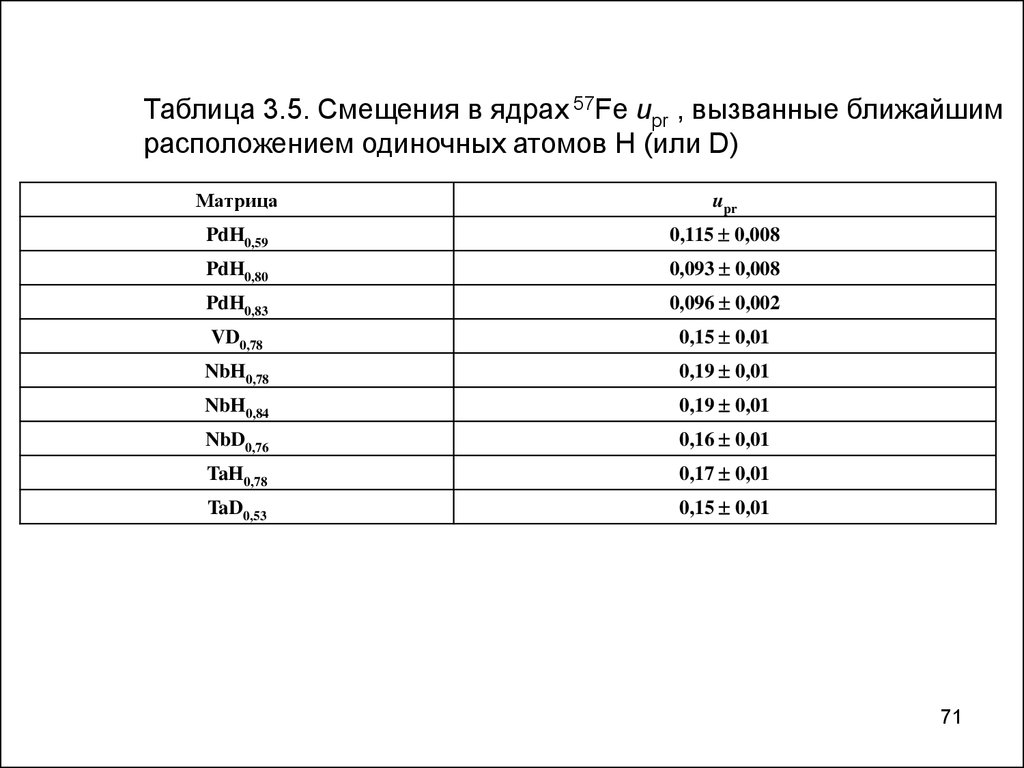
71.

Таблица 3.5. Смещения в ядрах 57Fe upr , вызванные ближайшим
расположением одиночных атомов H (или D)
Матрица
upr
PdH0,59
0,115 0,008
PdH0,80
0,093 0,008
PdH0,83
0,096 0,002
VD0,78
0,15 0,01
NbH0,78
0,19 0,01
NbH0,84
0,19 0,01
NbD0,76
0,16 0,01
TaH0,78
0,17 0,01
TaD0,53
0,15 0,01
71