Водород в металлах. Деформации решетки металла, связанные с водородом

1. Лекция 2 Водород в металлах

Деформации решетки металла,
связанные с водородом
1

2.

Поле деформаций для точечного дефекта
Введение межузельного атома в кристаллическую решетку в
общем случае сопровождается увеличением ее объема.
Добавочный объем на один межузельный атом v можно
определить исходя из изменения среднего межатомного расстояния
в решетке, т. е. увеличения постоянной решетки a. Так
называемый размерный фактор = a-1 ( a/ c) связан с v
соотношением v = 3 ; через с обозначена концентрация
примесных атомов в междоузлиях (количество межузельных
атомов/число атомов матрицы).
В общем случае смещения и атомов решетки из равновесных
положений r могут быть анизотропными, и поле деформаций
обусловленных межузельными атомами, описывается тензорной
величиной
dj
i
2

3.

Для примеси внедрения, характеризующейся тензором, могут
существовать эквивалентные ориентации v в кристаллической
решетке; в этом случае
nd
ij d
ij c ,
1
где v – доля примесей внедрения, имеющих ориентацию v.,
3

4.

Поле напряжений для точечного дефекта
Канзаки ввел следующую полезную для теоретического
описания поля смещений концепцию. Действительные
смещения атомов решетки, обусловленные дефектом,
можно имитировать, рассматривая решетку без дефектов и
вводя виртуальные силы
f jm
("силы Канзаки"). Эти силы действуют на каждый атом т
(находящийся на расстоянии xim от дефектного узла), так что
результирующие смещения оказываются такими же, как и
при введении дефектного атома. Распределение сил можно
описать с помощью мультипольного разложения по аналогии
с распределением зарядов в случае электрического поля.
4

5.

Оказывается, что в большинстве случаев можно ограничиться
только «дипольной частью» силового распределения
Pij
m
m
f j xi ,
m
Это так называемый дипольно-упругий тензор. Для получения
удовлетворительного описания смещений достаточно знать
силы, действующие только на несколько соседних атомов
(например, на ближайших соседей дефекта).
5

6.

6

7.

7

8.

Экспериментальны методы
Изменение макроскопических размеров
Растворение п атомов Н в металле приводит к изменению объема
металла V на величину
V n v,
где v – изменение объема на атом Н, т. е. величина, которая нас
интересует. Величина v непосредственно связана со средним
парциальным молярным объемом Vм = vL, где L - число Авогадро.
Металлический кристалл объемом V содержит N атомов металла.
Если средний объем на атом металла равен
, то V = N и относительное изменение объема, обусловленное Н,
атомная концентрация которого есть с = n/N, дается величиной
V / V c( v / ).
Для кубического кристалла со случайным распределением примесей
внедрения достаточно определить изменение одного из размеров
образца, например его длины L/L. При малых изменениях V/V=
З L/L+ [3( L/L)2]+... и
L / L 1/ 3 c( v / ).
8

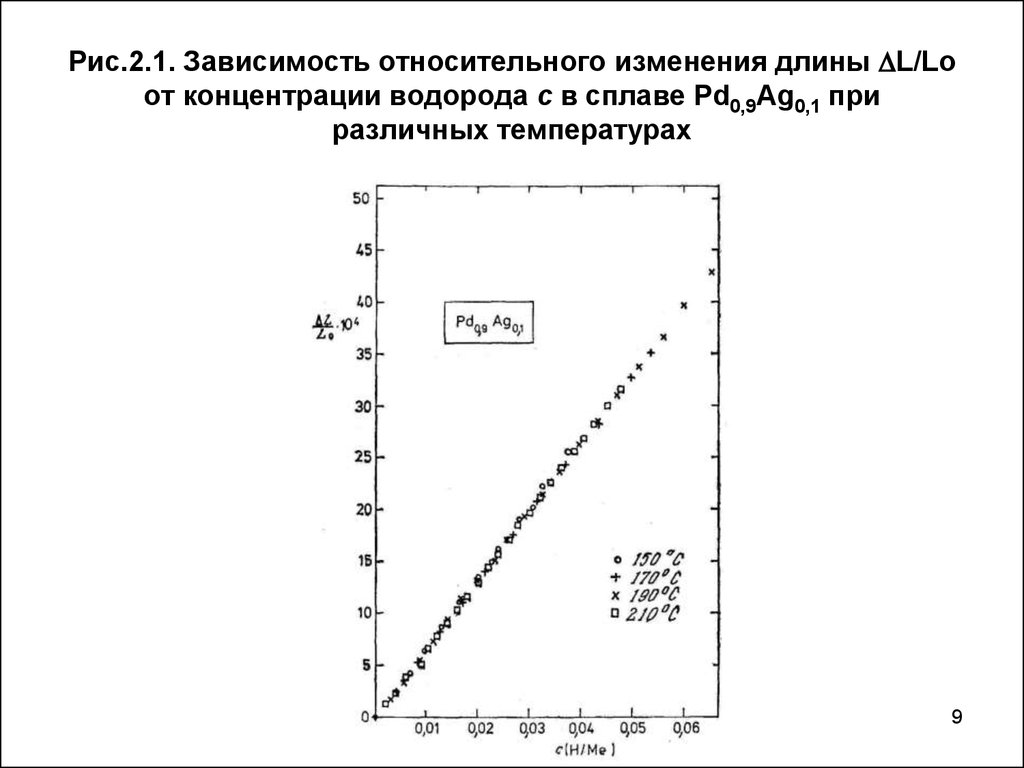
9. Рис.2.1. Зависимость относительного изменения длины L/Lo от концентрации водорода с в сплаве Pd0,9Ag0,1 при различных температурах

Рис.2.1. Зависимость относительного изменения длины L/Lo
от концентрации водорода с в сплаве Pd0,9Ag0,1 при
различных температурах
9

10.

Изменение постоянной решетки
Ту же информацию можно получить с помощью прецизионных
измерений постоянной решетки методами дифракции нейтронов
или рентгеновских лучей. Эти методы позволяют определить
изменение среднего объема элементарной ячейки, так что
полученные результаты не зависят от того, повлияли ли на
изменение объема в процессе растворения Н какие-либо побочные
явления, как то: испарение части атомов металла, утеря части
металлического порошка и т. п. Для кубического кристалла при
случайном расположении примесей в междоузлиях имеем
aH a0
3
a0
3
3
2
v
a
a
c
3
O 3
.
a
a
Малые изменения постоянной решетки определяются по сдвигу B
брэгговского отражения на больший угол ( B – угол Брэгга):
a / a ctg B B .
10

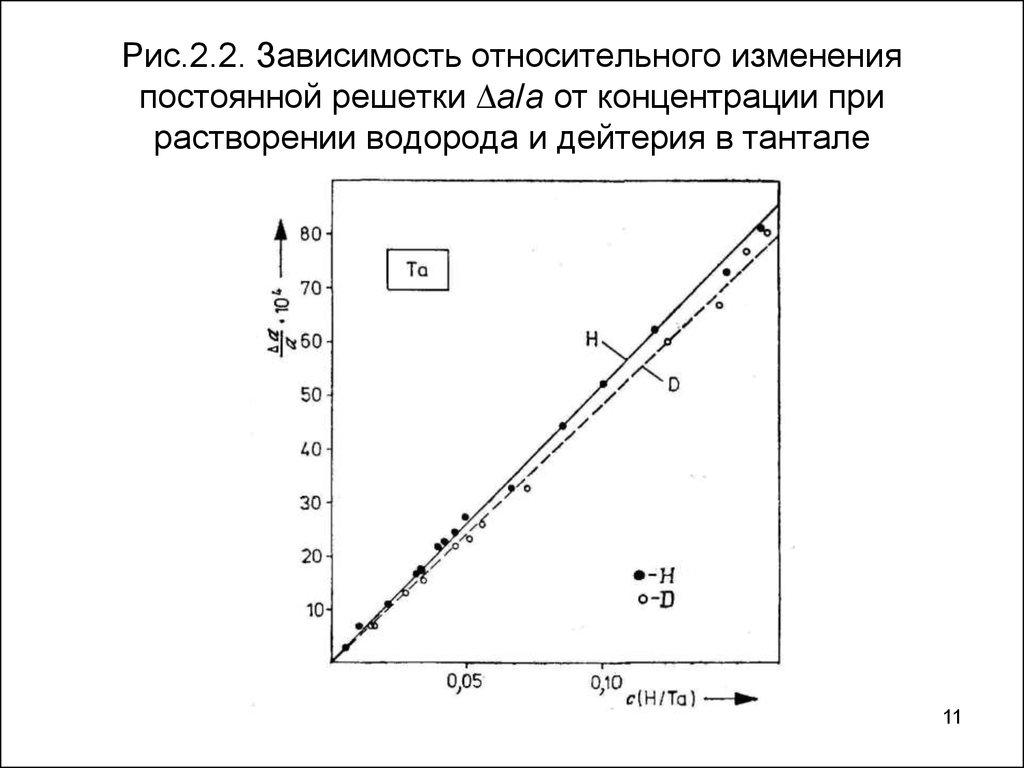
11. Рис.2.2. Зависимость относительного изменения постоянной решетки a/a от концентрации при растворении водорода и дейтерия в тантале

Рис.2.2. Зависимость относительного изменения
постоянной решетки a/a от концентрации при
растворении водорода и дейтерия в тантале
11

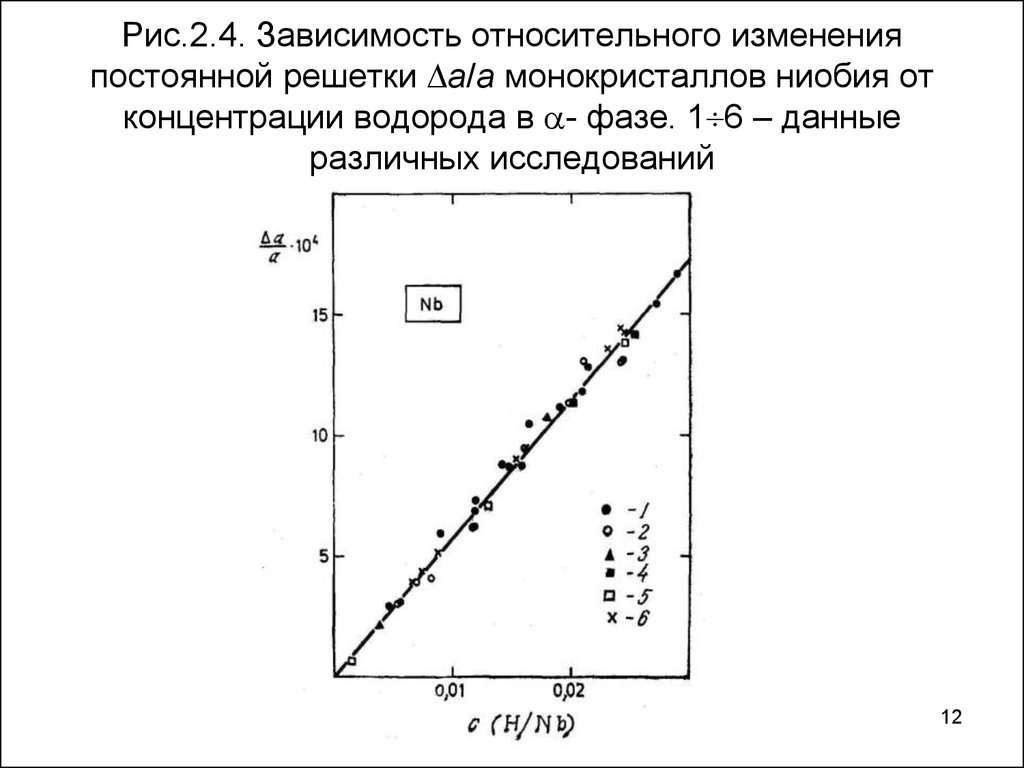
12. Рис.2.4. Зависимость относительного изменения постоянной решетки a/a монокристаллов ниобия от концентрации водорода в - фазе. 16 – данные

Рис.2.4. Зависимость относительного изменения
постоянной решетки a/a монокристаллов ниобия от
концентрации водорода в - фазе. 1 6 – данные
различных исследований
12

13. Рис.2.5. Зависимость относительного изменения объема V/V от концентрации в системе ниобий-водород. 17 – данные различных исследований

Рис.2.5. Зависимость относительного изменения
объема V/V от концентрации в системе ниобийводород. 1 7 – данные различных исследований
13

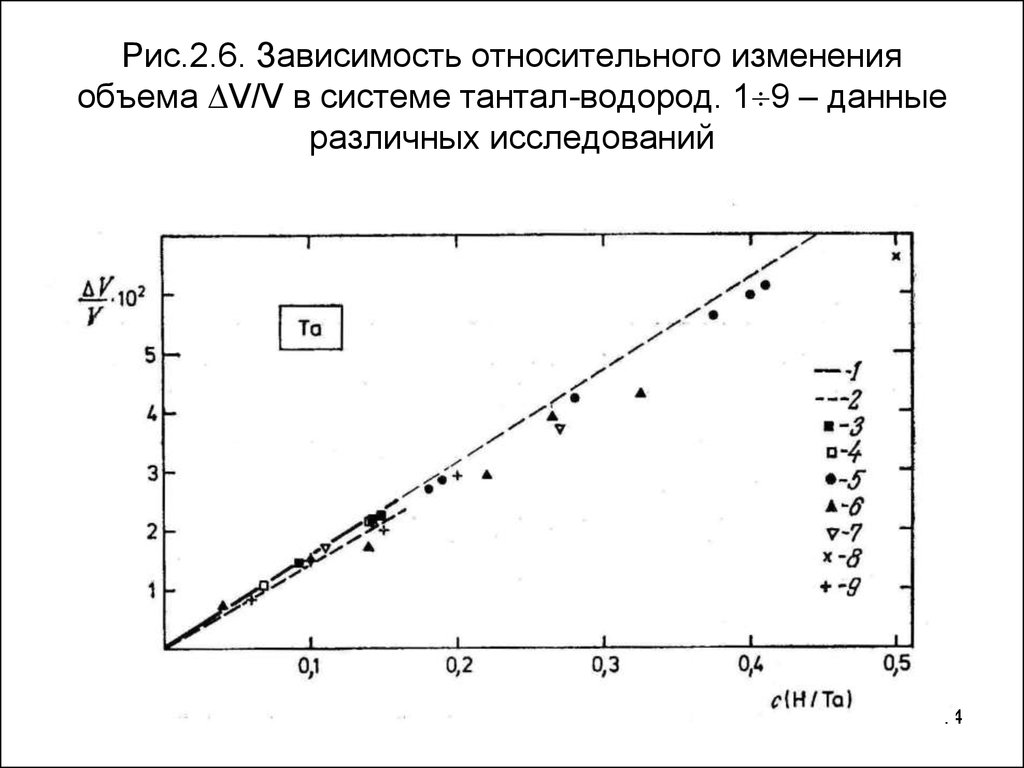
14. Рис.2.6. Зависимость относительного изменения объема V/V в системе тантал-водород. 19 – данные различных исследований

Рис.2.6. Зависимость относительного изменения
объема V/V в системе тантал-водород. 1 9 – данные
различных исследований
14

15.

Методы механической релаксации
Переориентация анизотропных упругих диполей во внешнем
поле деформаций приводит к появлению неупругой релаксации
(эффект
Снука).
Если
дефекты
обладают
высокой
подвижностью, как, например, Н в металлах, то возникает
диффузионная релаксация в условиях градиента деформации
(эффект Горского).
Для Н в ОЦК металлах, по-видимому, выполняются все условия,
необходимые для наблюдения этих релаксационных процессов.
Растворение Н вызывает расширение решетки; в ОЦК структуре
не существует междоузлий, обладающих полной кубической
симметрией. Было экспериментально доказано, что Н в Nb и Та
занимает тетраэдрические междоузлия; по этой причине следует
ожидать, что упругий диполь будет анизотропным, а Н будет
иметь
высокую
подвижность.
Характерная
величина
коэффициента диффузии при комнатной температуре: D 5·10-9
м2/с-1.
15

16.

Эффект Горского применяется главным образом для
прецизионных
измерений
коэффициента
диффузии.
Существует
еще
одна
наблюдаемая
величина
установившаяся неупругая деформация a. Эта величина,
нормированная на величину упругой внешней деформации
е, носит название релаксационной силы = a/ е. При
малой концентрации Н она определяется выражением
a (t )
a 3c( v / )2
E
G
.
e
18k B S11T
Здесь G – зависящий от ориентации множитель, который
содержит упругие модули и направляющие косинусы; kB–
постоянная Больцмана; Т–температура; S11–коэффициент
упругой податливости
16

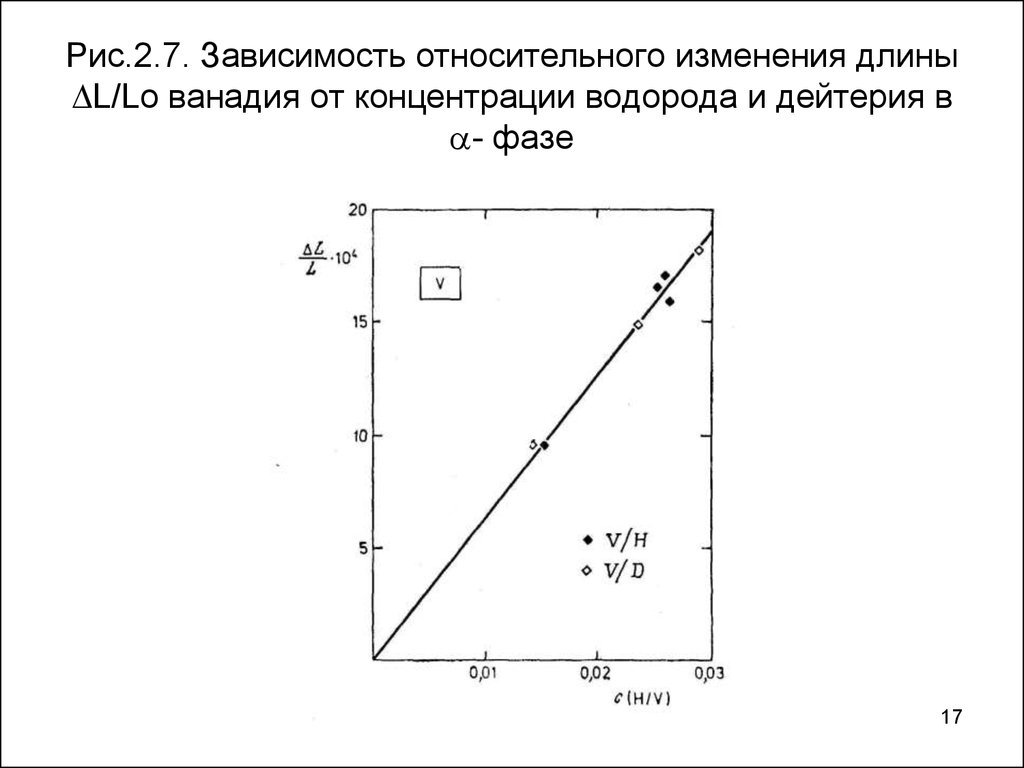
17. Рис.2.7. Зависимость относительного изменения длины L/Lo ванадия от концентрации водорода и дейтерия в - фазе

Рис.2.7. Зависимость относительного изменения длины
L/Lo ванадия от концентрации водорода и дейтерия в
- фазе
17

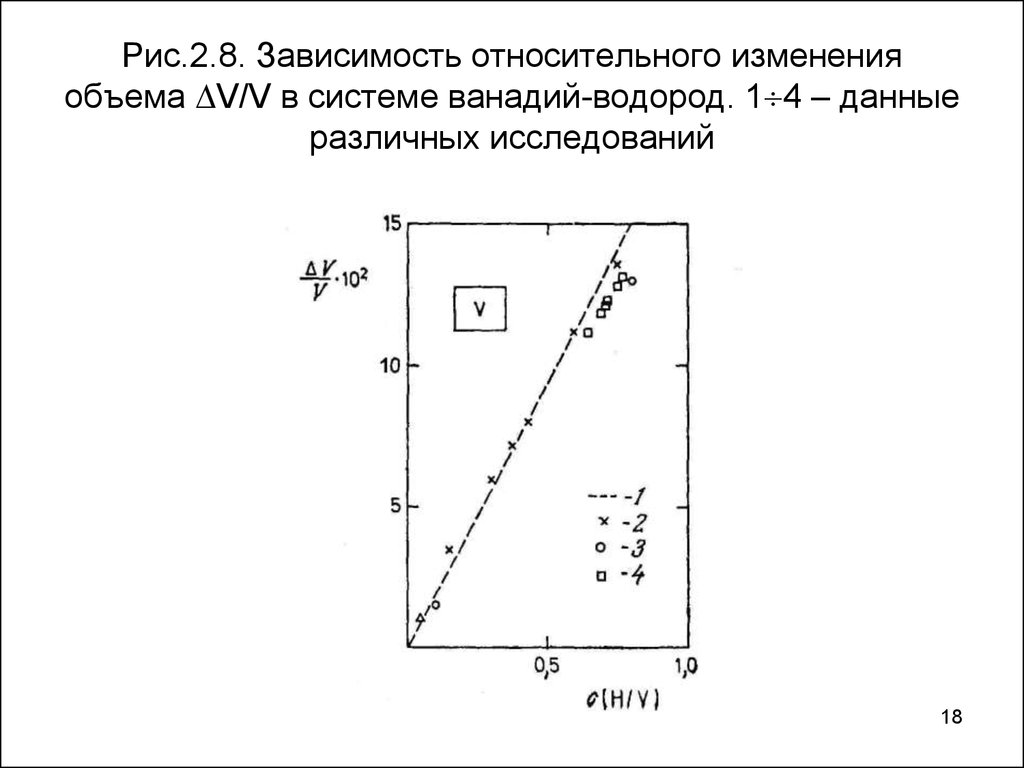
18. Рис.2.8. Зависимость относительного изменения объема V/V в системе ванадий-водород. 14 – данные различных исследований

Рис.2.8. Зависимость относительного изменения
объема V/V в системе ванадий-водород. 1 4 – данные
различных исследований
18

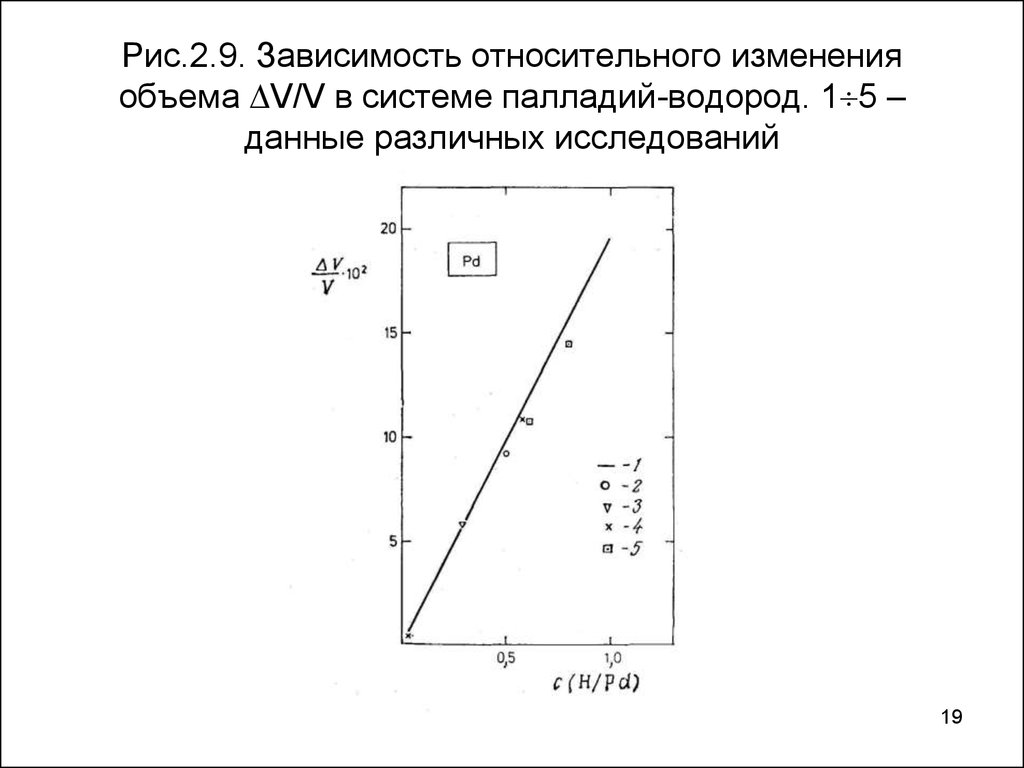
19. Рис.2.9. Зависимость относительного изменения объема V/V в системе палладий-водород. 15 – данные различных исследований

Рис.2.9. Зависимость относительного изменения
объема V/V в системе палладий-водород. 1 5 –
данные различных исследований
19

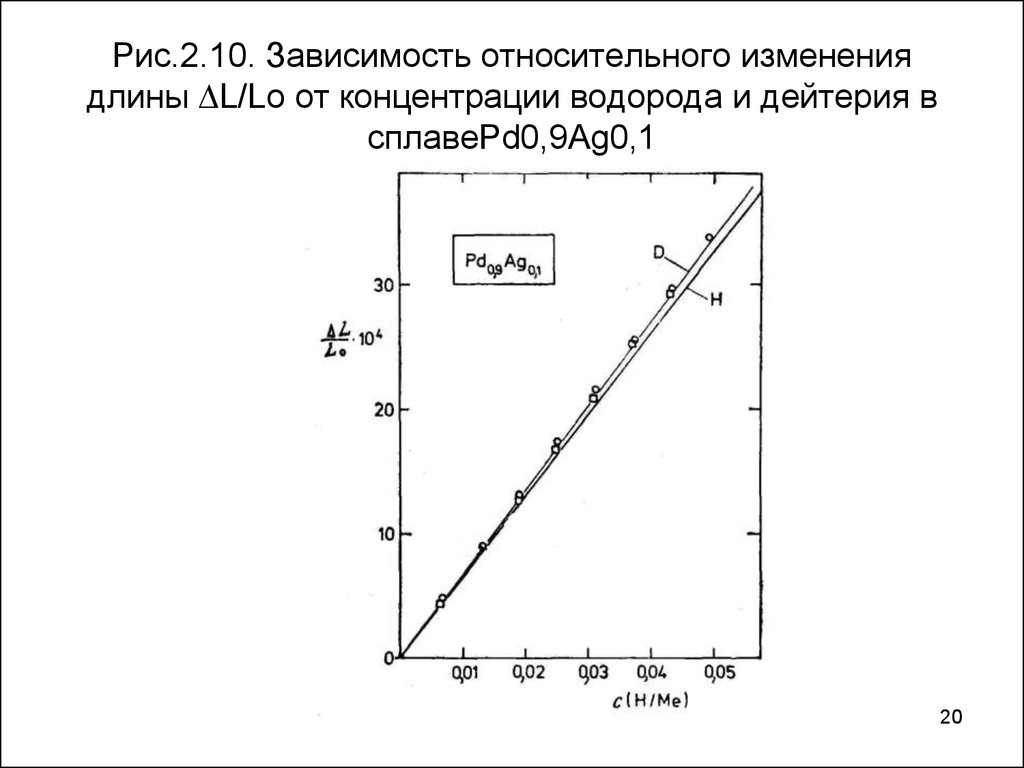
20. Рис.2.10. Зависимость относительного изменения длины L/Lo от концентрации водорода и дейтерия в сплавеPd0,9Ag0,1

Рис.2.10. Зависимость относительного изменения
длины L/Lo от концентрации водорода и дейтерия в
сплавеPd0,9Ag0,1
20

21.

Эффект Снука. Если приложить одноосное напряжение,
например, вдоль одной из главных осей кристалла, то будет
наблюдаться зависящее от времени упорядочение
анизотропных упругих диполей. Эта неупругая релаксация
пропорциональна ( 1- 2) или А - В для тетрагонального поля
деформаций. Она может быть обнаружена по изменениям
упругих модулей. Были исследованы модули сдвига С' = (С11C12)/2, C44 и модуль всестороннего сжатия В = (С11 + 2C12)/3.
Для малых концентраций дефектов и тетрагональных
деформаций изменение С должно иметь следующий вид:
2 c
C
( 1 2 )2 .
3kBT
Тщательные измерения эффекта Снука в сплавах Ме-Н дали
неожиданно малое значение 1- 2, которое практически лежало
в пределах погрешностей эксперимента.
21

22. Рис.2.3. Интенсивность диффузного рассеяния в ниобии, легированном водородом, близи пика отражения (330) в направлениях [110], [110] и [001]

Рис.2.3. Интенсивность диффузного рассеяния в
ниобии, легированном водородом, близи пика
отражения (330) в направлениях [110], [ 110] и [001]
22

23.

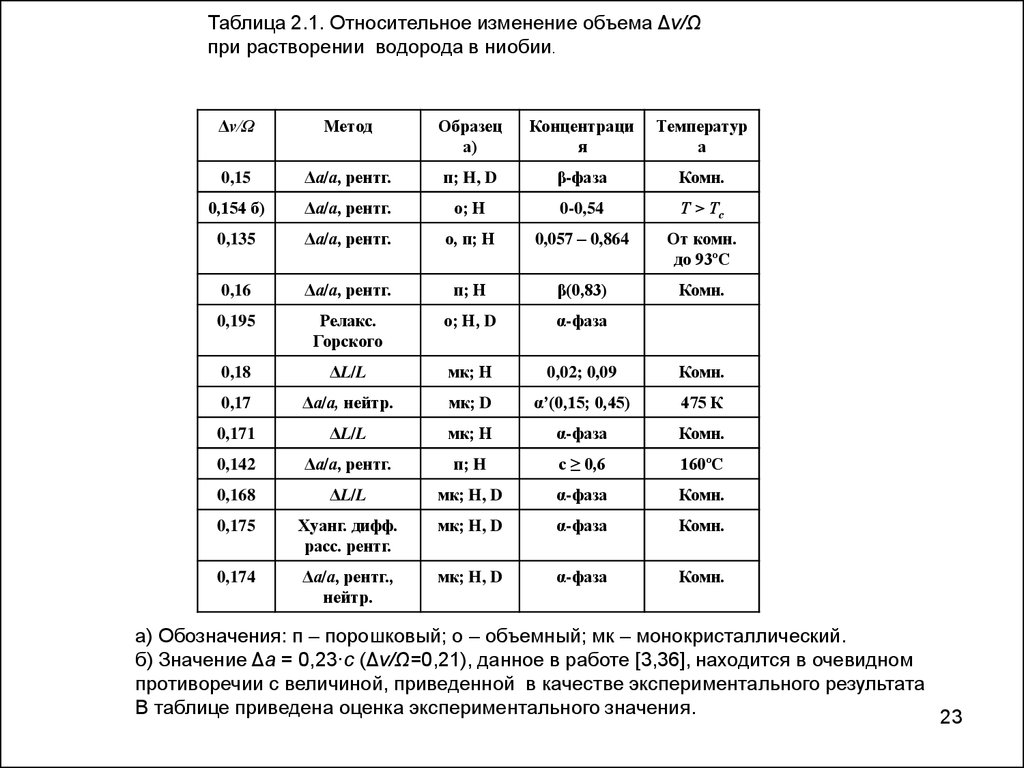
Таблица 2.1. Относительное изменение объема Δv/Ω
при растворении водорода в ниобии.
Δv/Ω
Метод
Образец
а)
Концентраци
я
Температур
а
0,15
Δа/а, рентг.
п; H, D
β-фаза
Комн.
0,154 б)
Δа/а, рентг.
о; Н
0-0,54
Т > Тс
0,135
Δа/а, рентг.
о, п; Н
0,057 – 0,864
От комн.
до 93ºС
0,16
Δа/а, рентг.
п; Н
β(0,83)
Комн.
0,195
Релакс.
Горского
о; Н, D
α-фаза
0,18
ΔL/L
мк; Н
0,02; 0,09
Комн.
0,17
Δа/а, нейтр.
мк; D
α’(0,15; 0,45)
475 К
0,171
ΔL/L
мк; Н
α-фаза
Комн.
0,142
Δа/а, рентг.
п; H
с ≥ 0,6
160ºС
0,168
ΔL/L
мк; H, D
α-фаза
Комн.
0,175
Хуанг. дифф.
расс. рентг.
мк; H, D
α-фаза
Комн.
0,174
Δа/а, рентг.,
нейтр.
мк; H, D
α-фаза
Комн.
а) Обозначения: п – порошковый; о – объемный; мк – монокристаллический.
б) Значение Δа = 0,23·с (Δv/Ω=0,21), данное в работе [3,36], находится в очевидном
противоречии с величиной, приведенной в качестве экспериментального результата
В таблице приведена оценка экспериментального значения.
23

24.

Ниобий
v/ = 0,174 ± 0,005.
Тантал
v/ = 0,155 ±0,005
Ванадий
Палладий
v/ = 0,19 ±0,01
v/ = 0,19±0,01
24

25. Рис.2.11. Зависимость изменения объема V от концентрации с водорода для ряда ГЦК металлов и сплавов в однофазной области (25 °С). 1 – палладий;

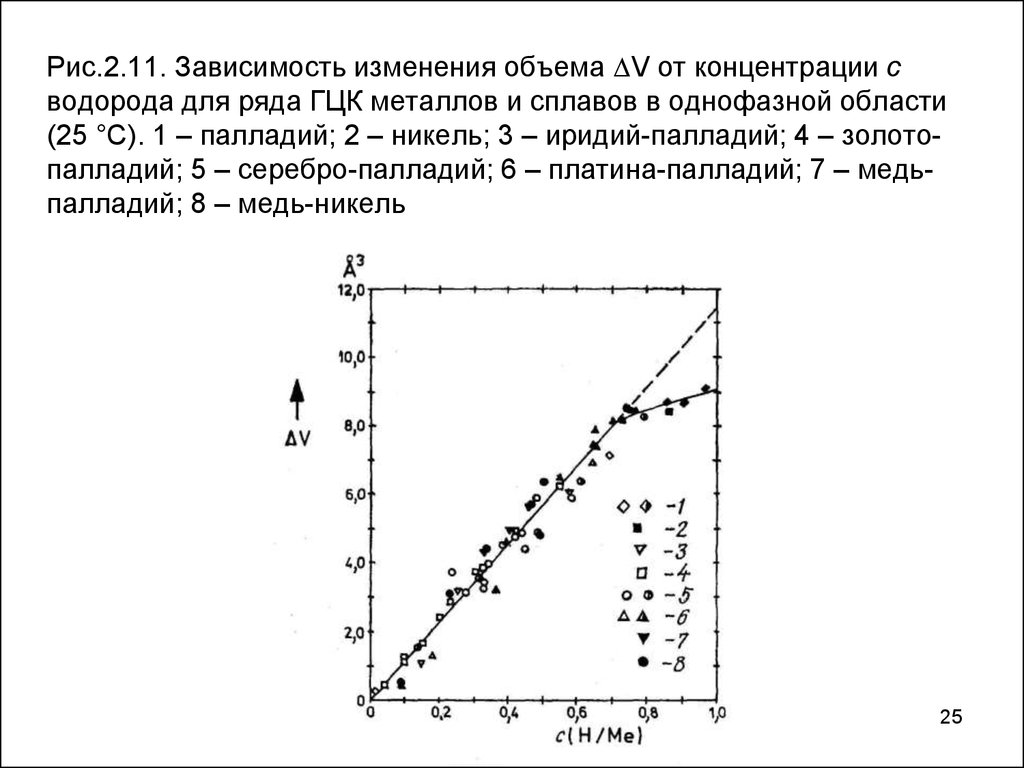
Рис.2.11. Зависимость изменения объема V от концентрации с
водорода для ряда ГЦК металлов и сплавов в однофазной области
(25 °С). 1 – палладий; 2 – никель; 3 – иридий-палладий; 4 – золотопалладий; 5 – серебро-палладий; 6 – платина-палладий; 7 – медьпалладий; 8 – медь-никель
25

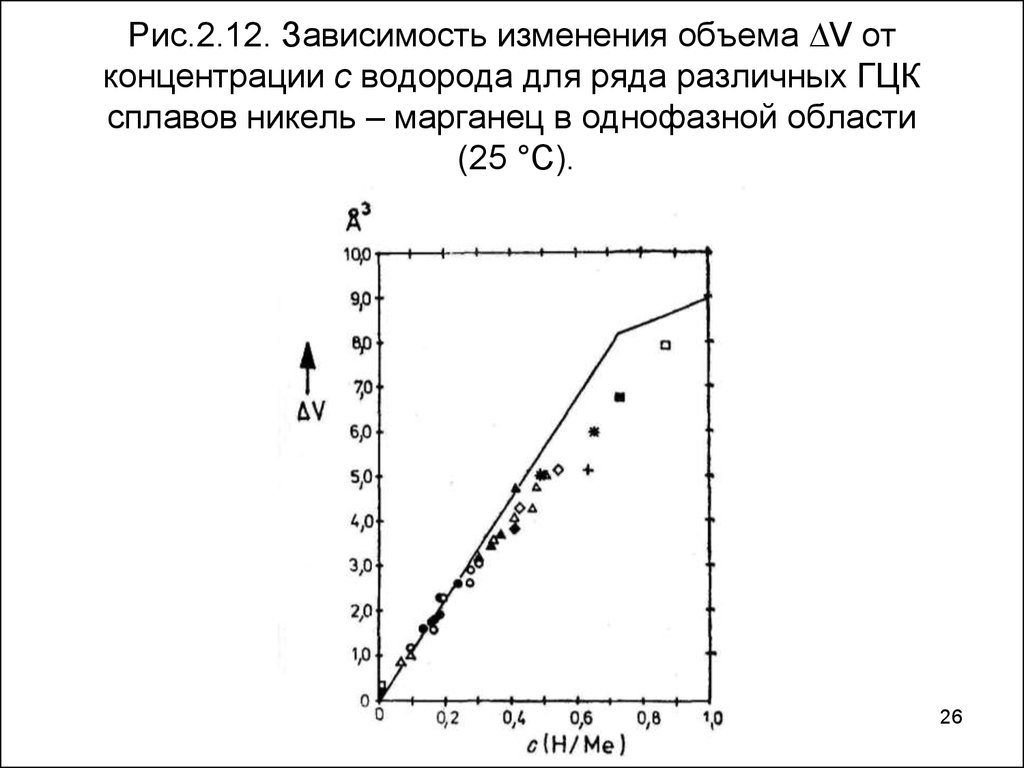
26. Рис.2.12. Зависимость изменения объема V от концентрации с водорода для ряда различных ГЦК сплавов никель – марганец в однофазной области (2

Рис.2.12. Зависимость изменения объема V от
концентрации с водорода для ряда различных ГЦК
сплавов никель – марганец в однофазной области
(25 °С).
26

27.

Данные по относительному изменению объема при
растворении Н в целом ряде ГЦК металлов и сплавов
показаны на рис. 2.11 и 2.12. Наклон экспериментальной
прямой имеет одну и ту же величину для самых разных
металлов и сплавов и соответствует значению v/с = 11,5 Å3
при 0 с 0,7.
Этот неожиданный результат означает, что при добавлении
одного атома Н объема кристалла изменяется на величину v =
2,9 Å3 независимо от материала. Объяснения этого единого
«размера» атома Н в самых разных материалах пока нет.
27