Тема 2.14 Простейшие тригонометрические неравенства

1. Решение простейших тригонометрических неравенств

2.

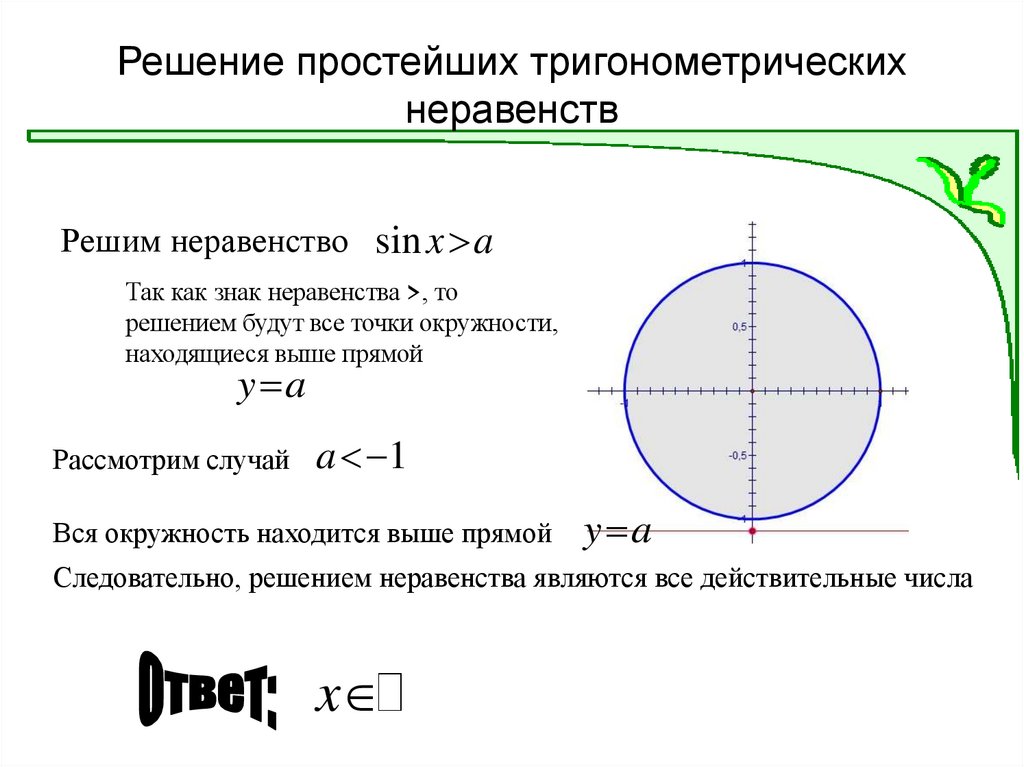
Неравенство sin x a

3. Решение простейших тригонометрических неравенств

Решим неравенство sin x a
Так как знак неравенства >, то
решением будут все точки окружности,
находящиеся выше прямой
y a
Рассмотрим случай
a 1
Вся окружность находится выше прямой
y a
Следовательно, решением неравенства являются все действительные числа
x

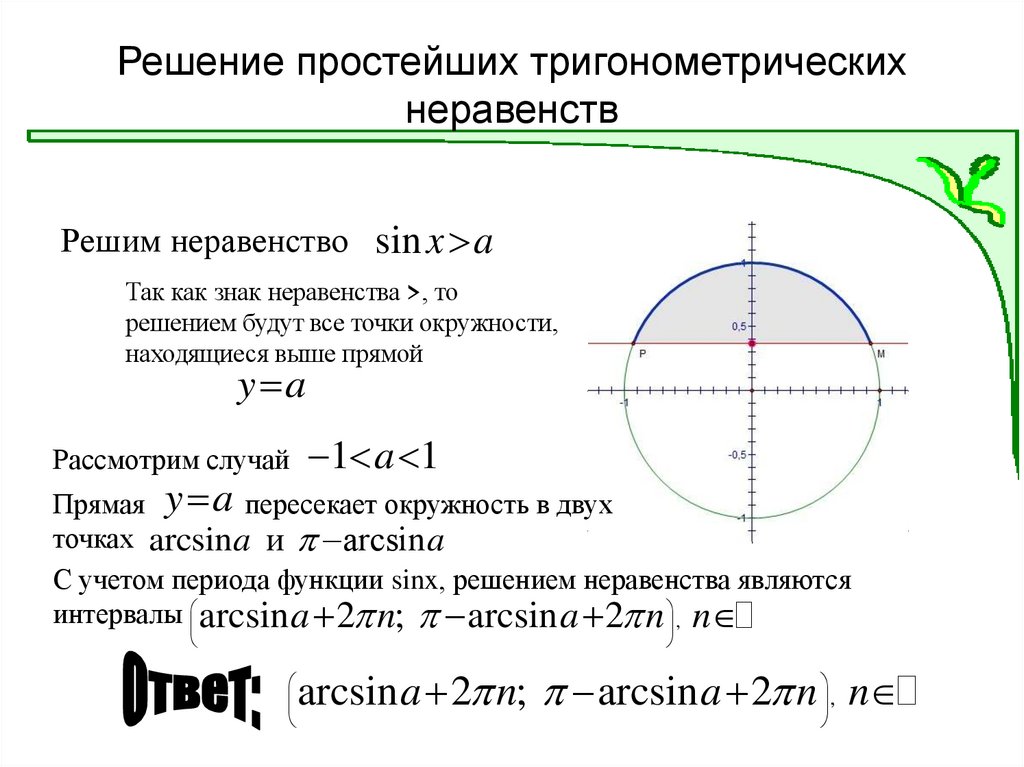
4. Решение простейших тригонометрических неравенств

Решим неравенство sin x a
Так как знак неравенства >, то
решением будут все точки окружности,
находящиеся выше прямой
y a
Рассмотрим случай 1 a 1
Прямая y a пересекает окружность в двух
точках arcsin a и arcsin a
С учетом периода функции sinx, решением неравенства являются
интервалы arcsin a 2 n; arcsin a 2 n , n
arcsin a 2 n; arcsin a 2 n , n

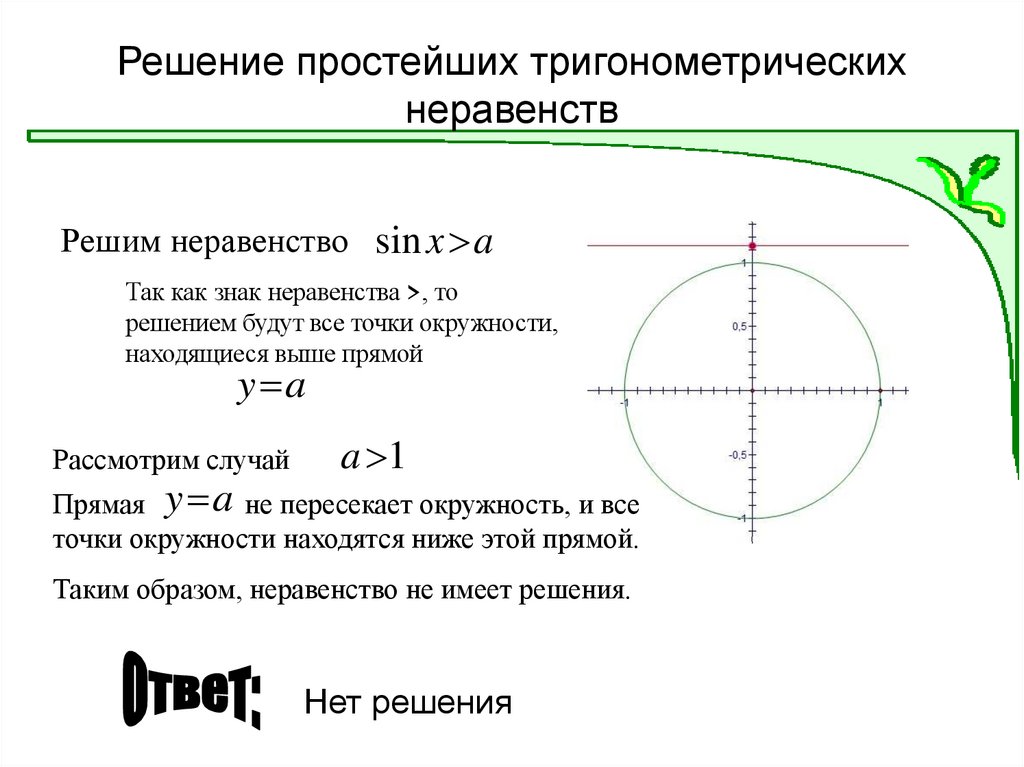
5. Решение простейших тригонометрических неравенств

Решим неравенство sin x a
Так как знак неравенства >, то
решением будут все точки окружности,
находящиеся выше прямой
y a
Рассмотрим случай
a 1
Прямая y a не пересекает окружность, и все
точки окружности находятся ниже этой прямой.
Таким образом, неравенство не имеет решения.
Нет решения

6.

7.

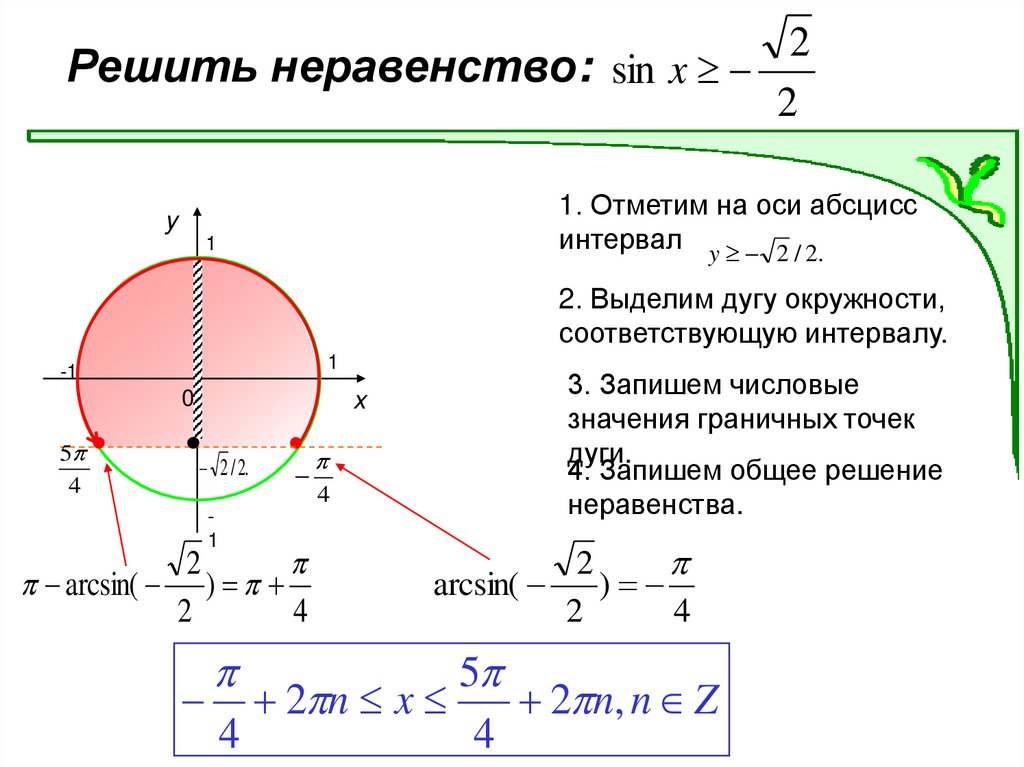
2
Решить неравенство: sin x
2
1. Отметим на оси абсцисс
интервал y 2 / 2.
y
1
2. Выделим дугу окружности,
соответствующую интервалу.
1
-1
0
5
4
x
2 / 2.
1
2
arcsin( )
2
4
4
3. Запишем числовые
значения граничных точек
дуги.
4. Запишем общее решение
неравенства.
2
arcsin(
)
2
4
5
2 n x
2 n, n Z
4
4

8.

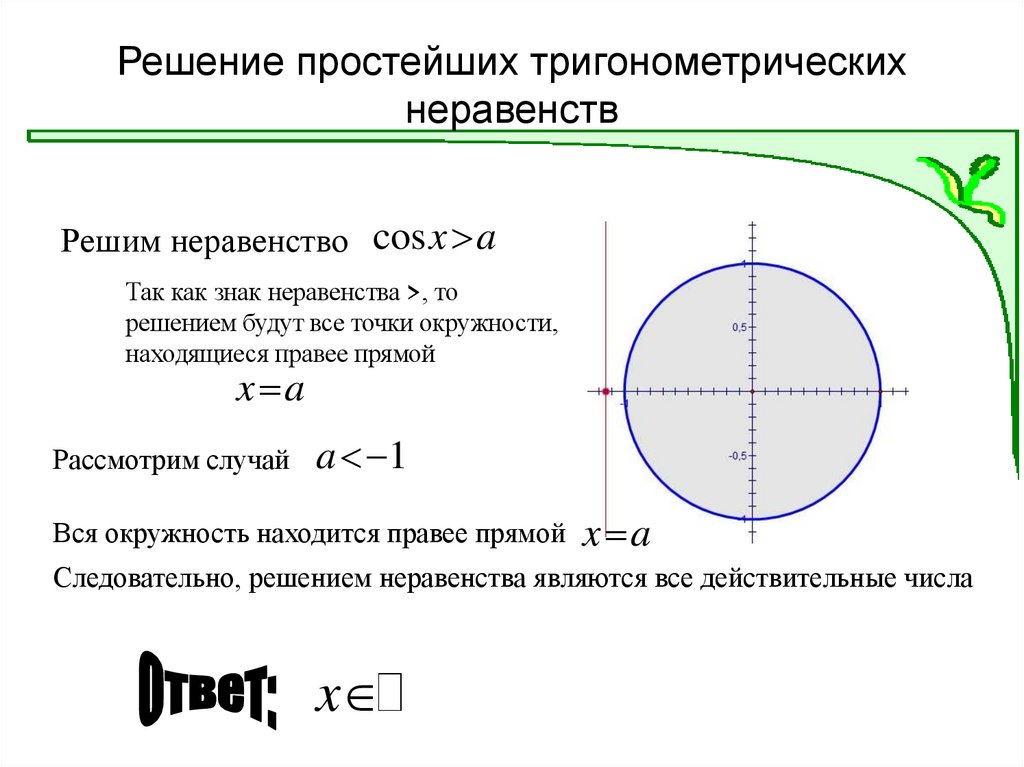
Неравенство cosx a

9. Решение простейших тригонометрических неравенств

Решим неравенство cosx a
Так как знак неравенства >, то
решением будут все точки окружности,
находящиеся правее прямой
x a
Рассмотрим случай
a 1
Вся окружность находится правее прямой x a
Следовательно, решением неравенства являются все действительные числа
x

10. Решение простейших тригонометрических неравенств

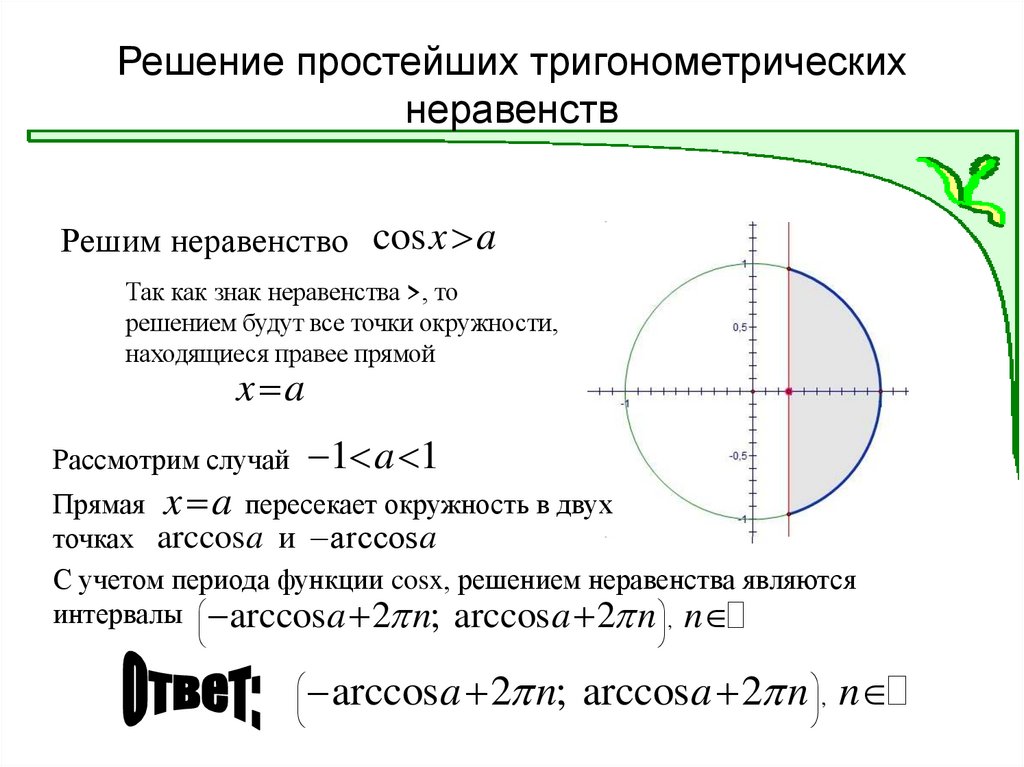
Решим неравенство cosx a
Так как знак неравенства >, то
решением будут все точки окружности,
находящиеся правее прямой
x a
Рассмотрим случай 1 a 1
Прямая x a пересекает окружность в двух
точках arccosa и arccosa
С учетом периода функции cosx, решением неравенства являются
интервалы arccos a 2 n; arccos a 2 n , n
arccosa 2 n; arccos a 2 n , n

11. Решение простейших тригонометрических неравенств

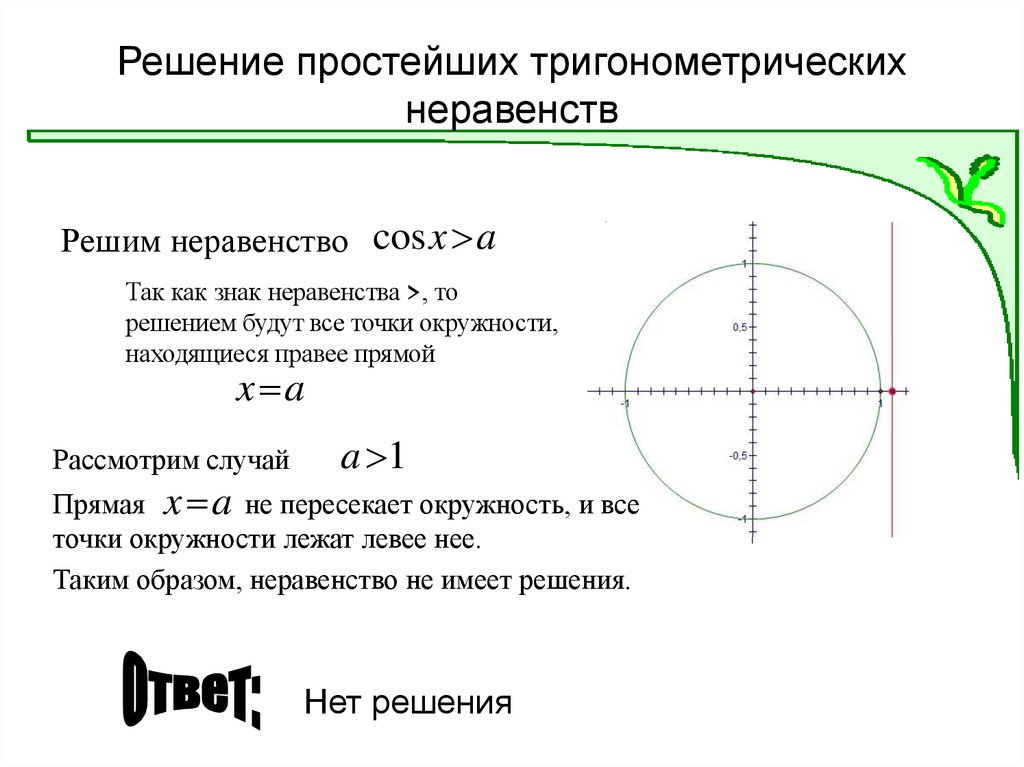
Решим неравенство cosx a
Так как знак неравенства >, то
решением будут все точки окружности,
находящиеся правее прямой
x a
Рассмотрим случай
a 1
Прямая x a не пересекает окружность, и все
точки окружности лежат левее нее.
Таким образом, неравенство не имеет решения.
Нет решения

12.

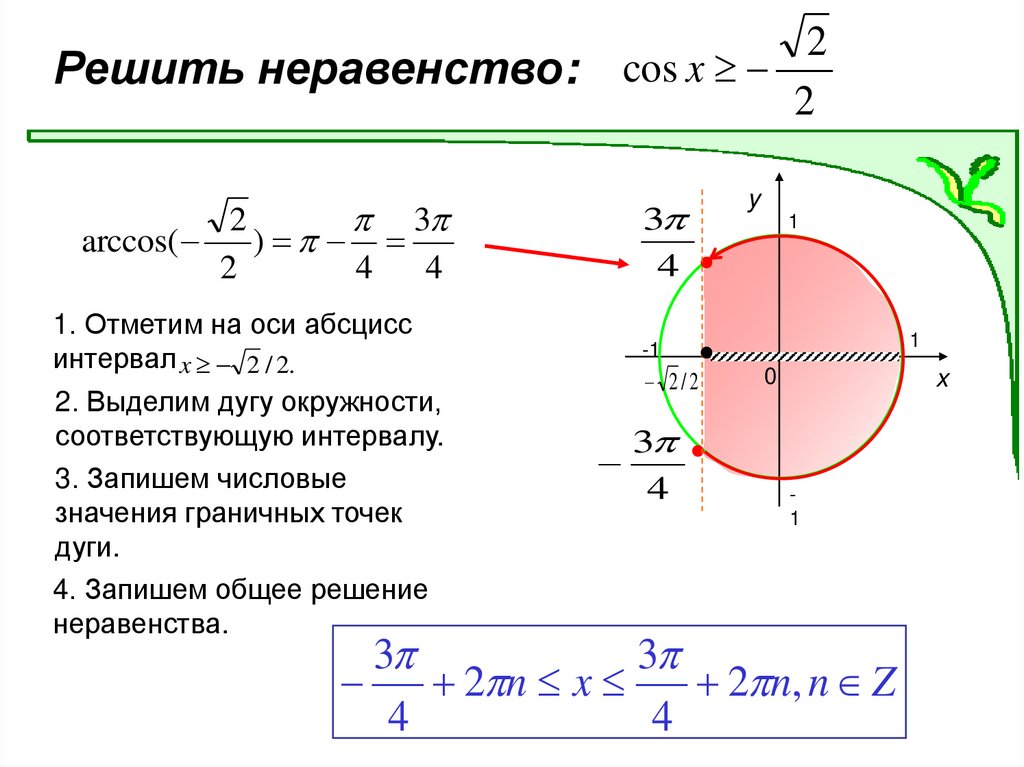
Решить неравенство:
2
3
arccos(
)
2
4
4
1. Отметим на оси абсцисс
интервал x 2 / 2.
2. Выделим дугу окружности,
соответствующую интервалу.
3. Запишем числовые
значения граничных точек
дуги.
4. Запишем общее решение
неравенства.
2
cos x
2
3
4
y
1
1
-1
2/2
3
4
0
x
1
3
3
2 n x
2 n, n Z
4
4

13.

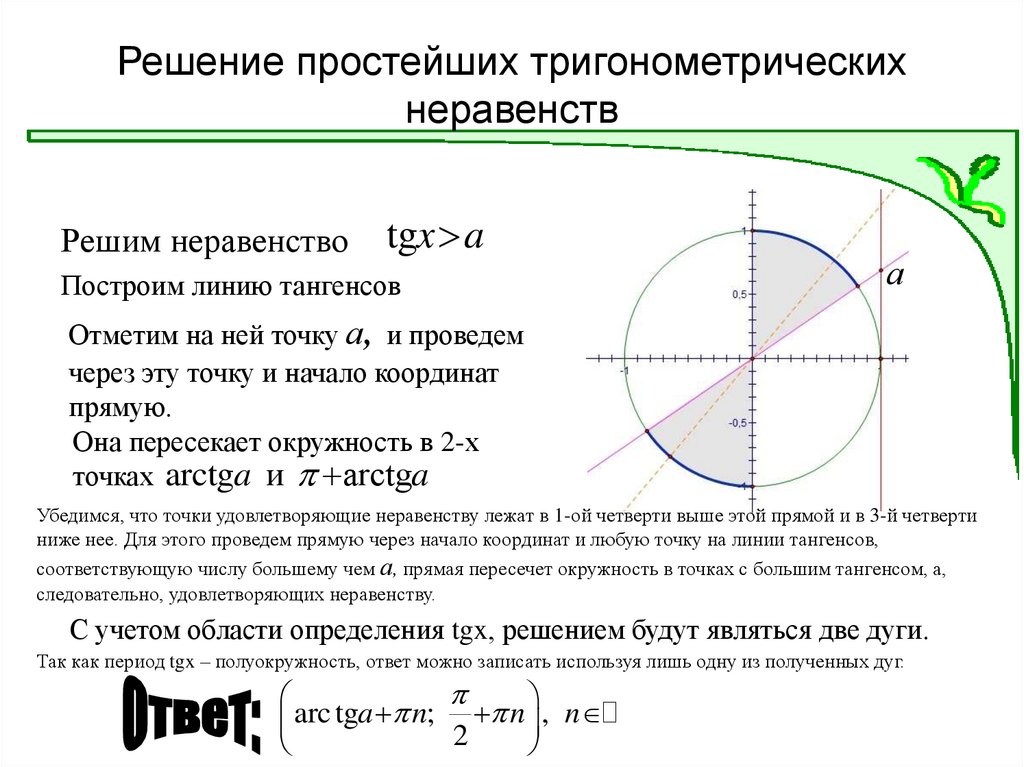
Неравенство tgx a

14. Решение простейших тригонометрических неравенств

Решим неравенство
tgx a
Построим линию тангенсов
а
Отметим на ней точку а, и проведем
через эту точку и начало координат
прямую.
Она пересекает окружность в 2-х
точках arctga и arctga
Убедимся, что точки удовлетворяющие неравенству лежат в 1-ой четверти выше этой прямой и в 3-й четверти
ниже нее. Для этого проведем прямую через начало координат и любую точку на линии тангенсов,
соответствующую числу большему чем а, прямая пересечет окружность в точках с большим тангенсом, а,
следовательно, удовлетворяющих неравенству.
С учетом области определения tgx, решением будут являться две дуги.
Так как период tgx – полуокружность, ответ можно записать используя лишь одну из полученных дуг.
arc
tg
a
n
;
n
, n
2

15.

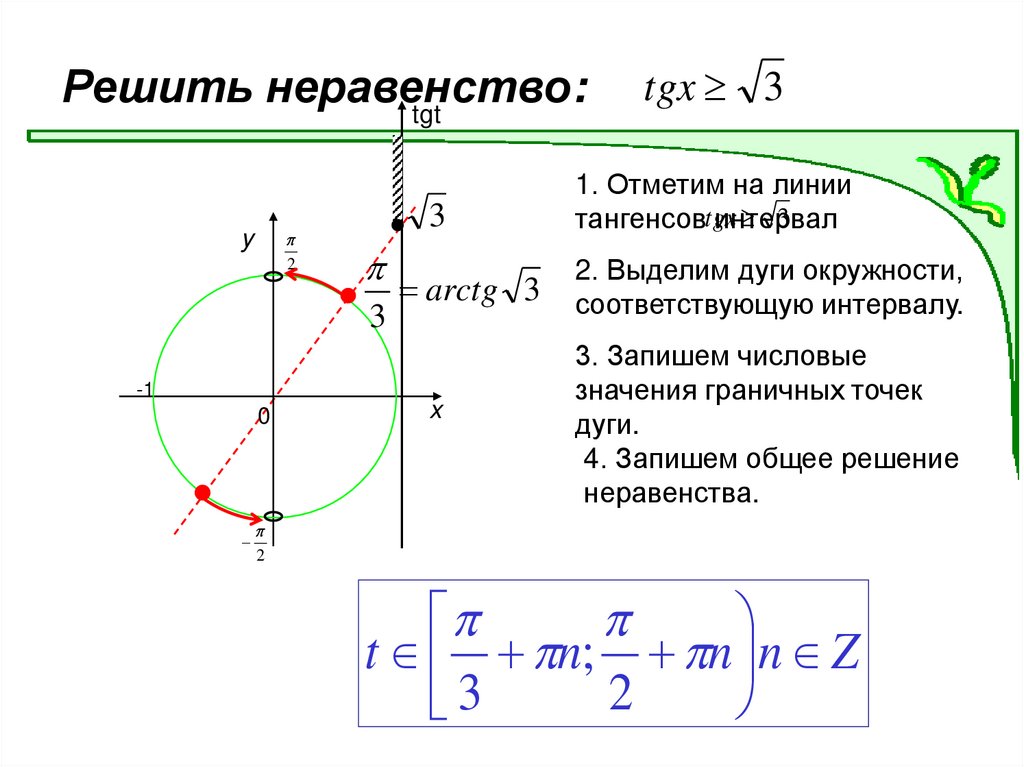
Решить неравенство:
tgt
2
y
3
3
-1
0
arctg 3
x
tgx 3
1. Отметим на линии
3
тангенсовtgx
интервал
2. Выделим дуги окружности,
соответствующую интервалу.
3. Запишем числовые
значения граничных точек
дуги.
4. Запишем общее решение
неравенства.
2
t n; n n Z
2
3

16.

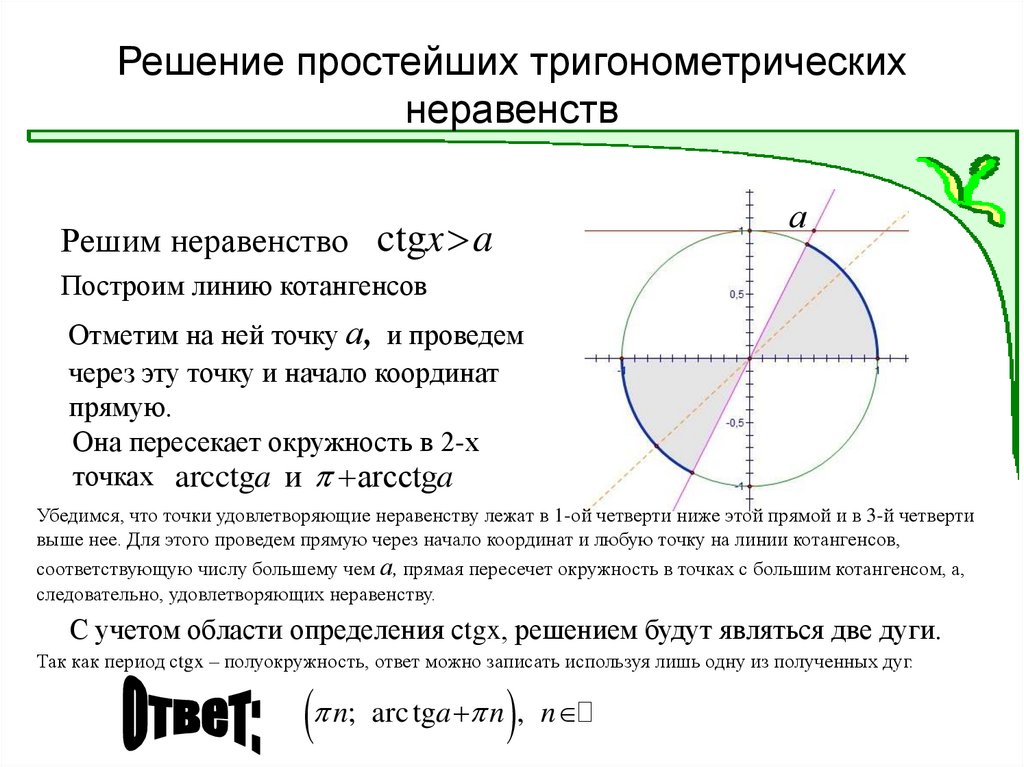
Неравенство ctgx a

17. Решение простейших тригонометрических неравенств

Решим неравенство ctgx a
а
Построим линию котангенсов
Отметим на ней точку а, и проведем
через эту точку и начало координат
прямую.
Она пересекает окружность в 2-х
точках arcctga и arcctga
Убедимся, что точки удовлетворяющие неравенству лежат в 1-ой четверти ниже этой прямой и в 3-й четверти
выше нее. Для этого проведем прямую через начало координат и любую точку на линии котангенсов,
соответствующую числу большему чем а, прямая пересечет окружность в точках с большим котангенсом, а,
следовательно, удовлетворяющих неравенству.
С учетом области определения сtgx, решением будут являться две дуги.
Так как период сtgx – полуокружность, ответ можно записать используя лишь одну из полученных дуг.
n; arc tga n , n

18.

Аналогично решаются неравенства
со знаком <

19.

Решить неравенство:
arcsin
y
1
6
2
-1
1
0
x
1
6
1
sin x
2
1
2 6
1. Отметим на оси абсцисс
интервал y < 1/2.
2. Выделим дугу окружности,
соответствующую интервалу.
3. Запишем числовые
значения граничных точек
дуги.
4. Записать общее решение
неравенства.
5
13
2 n x
2 n, n Z
6
6

20.

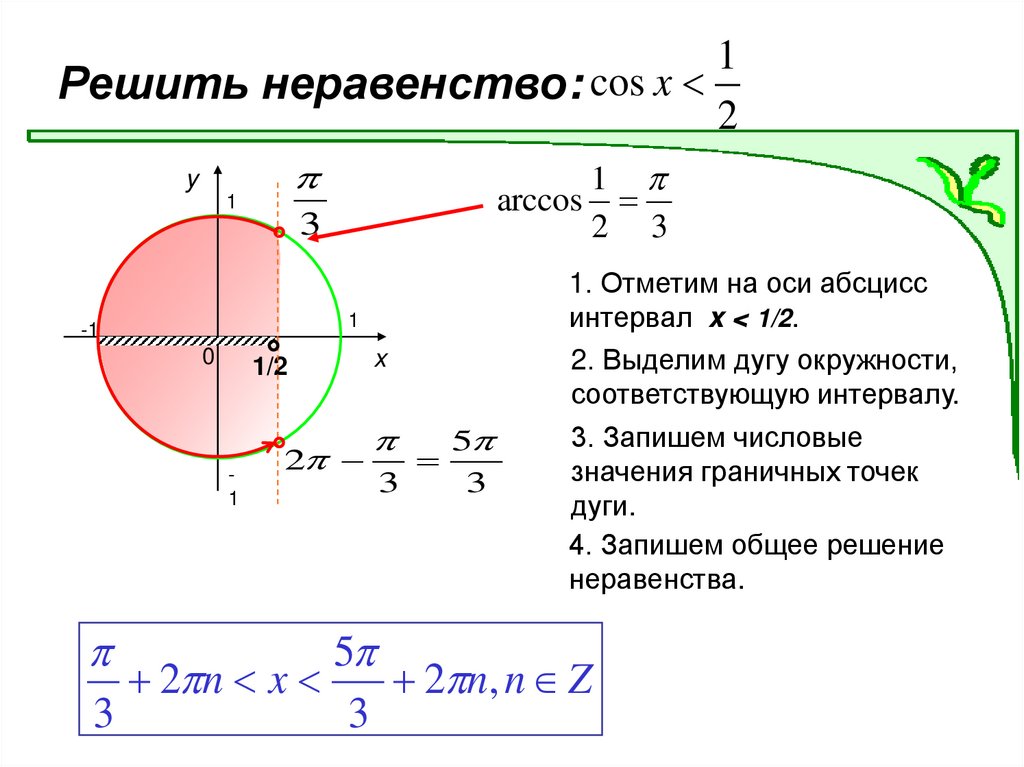
1
Решить неравенство: cos x
2
y
1
1
arccos
2 3
3
1
-1
0
1/2
1
2
x
3
5
3
1. Отметим на оси абсцисс
интервал x < 1/2.
2. Выделим дугу окружности,
соответствующую интервалу.
3. Запишем числовые
значения граничных точек
дуги.
4. Запишем общее решение
неравенства.
5
2 n x
2 n, n Z
3
3

21.

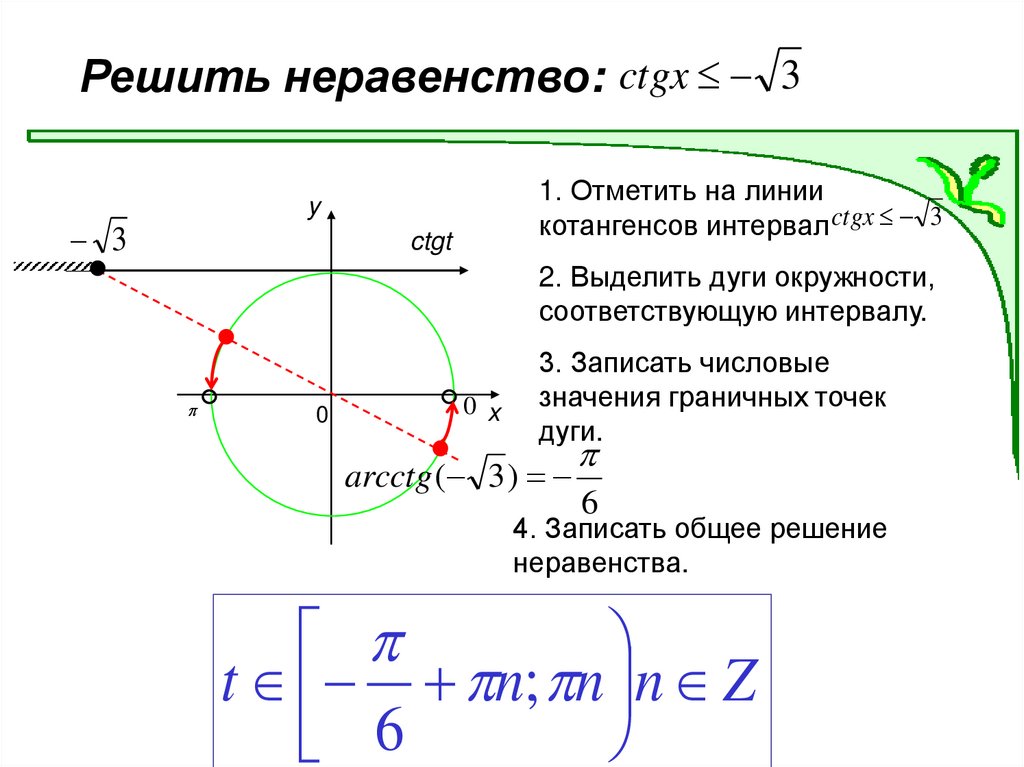
Решить неравенство: ctgx 3
1. Отметить на линии
котангенсов интервал ctgx 3
y
3
ctgt
2. Выделить дуги окружности,
соответствующую интервалу.
0
0 x
3. Записать числовые
значения граничных точек
дуги.
arcctg ( 3 )
6
4. Записать общее решение
неравенства.
t n; n n Z
6

22.

Формулы для решения простейших
тригонометрических неравенств