Similar presentations:
Лекция_15_Основные_методы_интегрирования,_интегрирование_рациональных
1. Лекция 15. Основные методы интегрирования, интегрирование рациональных функций. Интегрирование иррациональных и
тригонометрических функций.1
2.
§ 1. Метод интегрирования по частям.По значимости – это второй метод после метода
подстановки.
Формула интегрирования по частям является
обращением
формулы
дифференциала
произведения.
Пусть U=U(x) и V=V(x) – некоторые функции.
d(U·V)=dU·V+U·dV→UdV=d(U·V) – VdU.
2
3.
Проинтегрируем это равенство:∫UdV=U·V – ∫VdU
При взятии интеграла ∫d(U·V)=U·V
Данная формула позволяет свести вычисления
интеграла от ∫UdV к вычислению интеграла
∫VdU , что бывает намного проще.
3
4.
Пример 1.dx
arctgx U dU
2
arctg
xdx
1 x
dV dx
V x
xdx
1 2 xdx
x arctgx
x arctgx
2 1 x2
1 x2
1 d (1 x 2 )
1
2
x arctgx
x arctgx ln(1 x ) c.
2 1 x2
2
4
5.
Замечание. При вычислении интеграловметодом по частям требуется определённое
искусство в том, как лучше разбить
подынтегральное выражение так, чтобы ∫V·dU
был простым для вычисления.
Пример 2.
x U
dU dx
x
x
x
x e e dx
x e dx x
x
e
dx
dV
V
e
x
x
x e e c.
5
6.
II способ (тупиковый).x dx
x
e
2
x
x
1 2 x
e U
x
x
e
x e dx
x e dx
2
x
2
2
xdx
dV
V
2
При нерациональном выводе может получиться
более сложный интеграл.
Когда
мы
разбиваем
подынтегральное
выражение ∫UdV на U и dV, то dx содержится в
dV.
6
7.
Некоторые интегралы приходится брать дваждыпо частям:
2
dU 2 xdx
x
U
2
x sinxdx sinxdx dV V cos x
dU dx
x U
x cosx 2 x cos xdx
cos xdx dV V sinx
2
x cos x 2( x sinx sinxdx)
2
x cos x 2 xsinx 2 cos x c.
2
x cosxdx
Аналогично:
2
x
x
e
dx
2
7
8.
Интегралы вида: ∫x3sinxdx; ∫ x3cosxdx; ∫ x3exdx –берутся трижды по частям.
И вообще: xnsinxdx; ∫ xncosxdx; ∫ xnexdx берутся n
раз по частям. (Каждое применение метода по
частям понижает степень x на единицу.)
Случается так, что повторное применение к
интегралу метода интегрирования по частям
приводит интеграл к самому себе. В этом случае
мы имеем либо ничего не дающее тождество,
т.е.
интегрирование
было
проведено
нерационально, либо получаем линейное
уравнение относительно этого интеграла, и
откуда его находим.
8
9.
Пример . I= ∫exsinxdx;I= ∫excosxdx.
Пусть
x
x
e U
dU e dx
x
I e sinxdx
sinxdx dV V cos x
e cosx e cos xdx
x
x
x
e x U
dU e dx
cos xdx dV V sinx
e cos x e sinx e sinxdx
x
x
x
9
10.
I = ex (sinx – cosx) – I;2 I = ex (sinx – cosx);
I=(1/2) ex (sinx – cosx) + c
По значимости этот метод (после метода
подстановки) занимает 2 – е место, однако есть
интегралы, которые могут быть вычислены
только этим методом:
∫xneaxdx
xn = U
∫ xnsinaxdx
∫ xncosaxdx
∫xnlnmxdx
∫ xnarctgxdx
∫ xnarcsinxdx
lnx = U
10
11.
§ 2. Интегралы вида∫ Pn(x)dx; ∫ cosmxdx; ∫ sinmxdx (m, n ϵ N).
Pn(x)=a0+a1x+…+anxn
∫Pn(x)=a0∫dx+a1∫xdx+…+an∫xndx =a0x+a1(x2/2)+
+an(xn+1/n+1)+c.
∫ cosmxdx;
а). m=2k+1 (нечётная)
∫ cosmxdx = ∫ cos2k+1xdx = ∫ cos2kx·cosxdx =
= ∫ (cos2x)k·dsinx = ∫ (1 – sin2x)kdsinx = [sinx = t] =
= ∫ (1 – t2)kdt – получим интеграл от многочлена,
который легко вычисляется.
11
12.
б). m = 2k (чётная)∫ cosmxdx = ∫ cos2kxdx = ∫ (cos2x)kdx =
= ∫((1+cos2x)/2)kdx = (1/2k)∫(1+cos2x)kdx
Под знаком ∫ мы получили так называемый
тригонометрический многочлен, переменной в
котором является cos2x, причём многочлен в
степени k , т.е. в два раза ниже, чем была в
начале.
Далее
интегрируя
этот
тригонометрический многочлен:
∫(a0+a1cos2x+a2cos22x+…+akcosk2x)dx
Степени cos здесь чётные и нечётные, где
нечётные – доводим до конца, где чётные –
вновь понижаем в два раза, как это было в
начале.
12
13.
И так степень понижаем до тех пор, пока неполучим табличные интегралы.
Пример :
1). ∫ cos3xdx = ∫ cos2x·cosxdx = ∫ cos2x·dsinx =
= ∫ (1-sin2x)dsinx = [sinx = t] = ∫ (1 – t2)dt =
= t – (t3/3)+c = sinx – (1/3)sin3x+c.
2). ∫ cos2xdx = ∫((1+cos2x)/2)dx
∫cos4xdx = ∫(cos2x)2dx = ∫((1+cos2x)2/2)dx =
= (1/4)∫(1+2cos2x+cos22x)dx – нет проблем.
Относительно ∫ sinmxdx рассуждения
аналогичны, а именно:
13
14.
а). m = 2k + 1, и в этом случае:∫ sinmxdx = ∫ sin2k+1xdx = ∫ sin2kx·sinxdx =
= – ∫ (1-cos2x)kdcosx = [cosx = t]= ∫ (1 – t2)kdt
б). m = 2k. Здесь:
∫ sinmxdx = ∫ sin2kxdx = ∫((1 – cos2x)/2)kdx =
= (1/2k) ∫(1 – cos2x)kdx
14
15.
§ 3. Интегрирование рациональныхфункций.
Pn ( x)
f ( x)
– рациональная функция, где
Qm ( x)
Pn(x), Qm(x) многочлены соответствующих
степеней n и m , n,m ϵ N. По другому такие
функции называются рациональными дробями.
При этом рациональная дробь называется
правильной, если степень числителя строго
меньше степени знаменателя n < m , и
называется неправильной в противном случае
n ≥ m , т.е. степень числителя больше или равна
степени знаменателя.
15
16.
Простые рациональные дробиОпределение. Простыми рациональными
дробями называются функции вида:
A
A
,
x a ( x a)n
, n > 1 (1)
Ax B
Ax B
,
, n > 1, D < 0, т.е. (2)
2
2
n
x px q ( x px q )
p2 – 4q < 0
Дроби вида (1) называются простыми
рациональными дробями первого рода, и вида
(2) – второго рода
16
17.
Adx
dt
x a t
dx A
A
x a
x a dx dt
t
A ln t c A ln x a c
A
dx
dt
x a t
dx A
A
n
n
n
dx
dt
( x a)
( x a)
t
1
n
1
n
t
A ( x a)
n
A t dt A
c
c
1 n
1 n
17
18.
Ax Bdx *
2
x px q
x2+px+q=x2+2x·(p/2)+(p2/4 – (p2/4)+q =
= (x+(p/2)) 2 +q – (p2/4)
Заметим, что q – (p2/4) > 0
(4q – p2)/4) > 0 , т.к. p2 – 4q < 0
Это даёт нам основание ввести обозначение
q – (p2/4) = a2
18
19.
px
t
2
2
p
2
( Ax B)dx
p
*
x t q 4 a
2
2
p 2
p
( x ) (q
) dx dt
2
4
p
( A(t ) B)dt
tdt
Ap
2
A
(B )
2
t 2 a2
t 2 a2
dt
A d (t 2 a 2 )
Ap 1
t
( B ) arctg
2
2
2
2
2
2 a
a
t a
t a
19
20.
AAp 1
t
2
2
ln t a ( B ) arctg c
2
2 a
a
A
Ap
2
ln x px q ( B )
2
2
p
x
1
2 c
arctg
2
2
p
p
q
q
4
4
20
21.
n>1Ax B
( x 2 px q ) n
dx
( Ax B )
n
2
p 2
p
)
( x ) ( q
2
4
p
p
A(t ) B
2
x
t
p
2
2
q
a
dt
2
2 a 2 )n
4
(
t
dx dt
dx
tdt
Ap
dt
A
(B )
2
(t 2 a 2 ) n
(t 2 a 2 ) n
21
22.
22
tdt
1 d (t a )
2
2
I
t a U
(t 2 a 2 ) n 2 (t 2 a 2 ) n
1
n
1 dU 1 n
1U
U dU
c
2 Un 2
2 1 n
1 (t 2 a 2 )1 n
1 ( x 2 px q )1 n
c
c
2
1 n
2
1 n
22
23.
IIdt
2
2
n
(t a )
*
t a tgU
2
n
a
2
2
n
UdU (t a )
*
dt
2n U
cos
2
cos U
2
2
n
2
2
2
n
2
n
2
n
(t a ) (a tg U a ) a sec U
a 2n
2
n
cos U
2
n
U cos U
1
2
n
2
*
dU
cos U
UdU
cos 2 U U 2n
U 2n 1
23
24.
Теорема(о
разложении
правильной
рациональной дроби). Всякую рациональную
дробь можно представить в виде суммы простых
рациональных дробей (см. учебники).
Пример:
dx
I 2
( x 1)( x 2)
1
A
B
f ( x)
( x 1)( x 2) x 1 x 2
A( x 2) B( x 1) ( A B) x 2 A B
( x 1)( x 2)
( x 1)( x 2)
24
25.
1A
A
B
0
3
2 A B 1 B 1
3
1
1 1
1 1
( x 1)( x 2) 3 x 1 3 x 2
1 1
1 1
2
I 2 (
)dx ln x 1
3 x 1 3 x 2
3
2
2 x 1
ln x 2 c ln
c
3
3 x 2
Любая
правильная
рациональная
интегрируема.
дробь
25
26.
Алгоритм для вычисления правильнойрациональной дроби
1) Разложить на множители знаменатель дроби.
2) Представить эту дробь в виде суммы простых
рациональных дробей.
3) Проинтегрировать полностью полученную
сумму.
Пусть f(x)-неправильная рациональная дробь
Pn ( x)
f ( x)
Qm ( x) , n ≥ m
26
27.
В этом случае всегда можно разделитьчислитель на знаменатель. Результатом деления
будет либо многочлен (если нацело), либо сумма
многочлена и правильной рациональной дроби.
Рациональная функция всегда интегрируема.
«О разложении рациональной дроби в сумму
простых»
P( x)
Q( x)
Q( x) a ( x x ) 1 ( x x ) 2 ... ( x xn ) n
1
2
( x 2 p 1 x q 1 ) 1 ... ( x 2 p m x q m ) m
27
28.
P( x)( x 1)( x 2) 2 ( x 4) 4 ( x 2 1) ( x 2 2 x 2)3
A5
A3
A4
A2
A1
( x 1) ( x 2) ( x 2) 2 ( x 4) ( x 4) 2
A7
A6
B1x C1 B2 x C2
2
2
4
3
x 1 x 2x 2
( x 4)
( x 4)
B3 x C3
B4 x C4
3
2
2
2
( x 2 x 2)
( x 2 x 2)
28








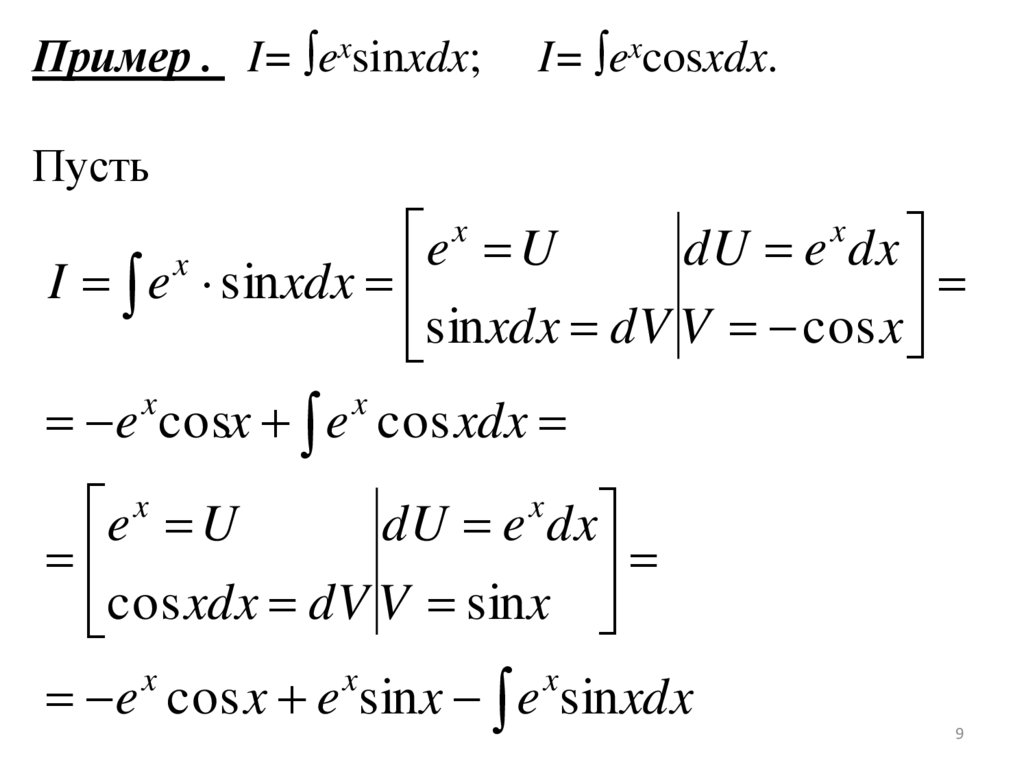




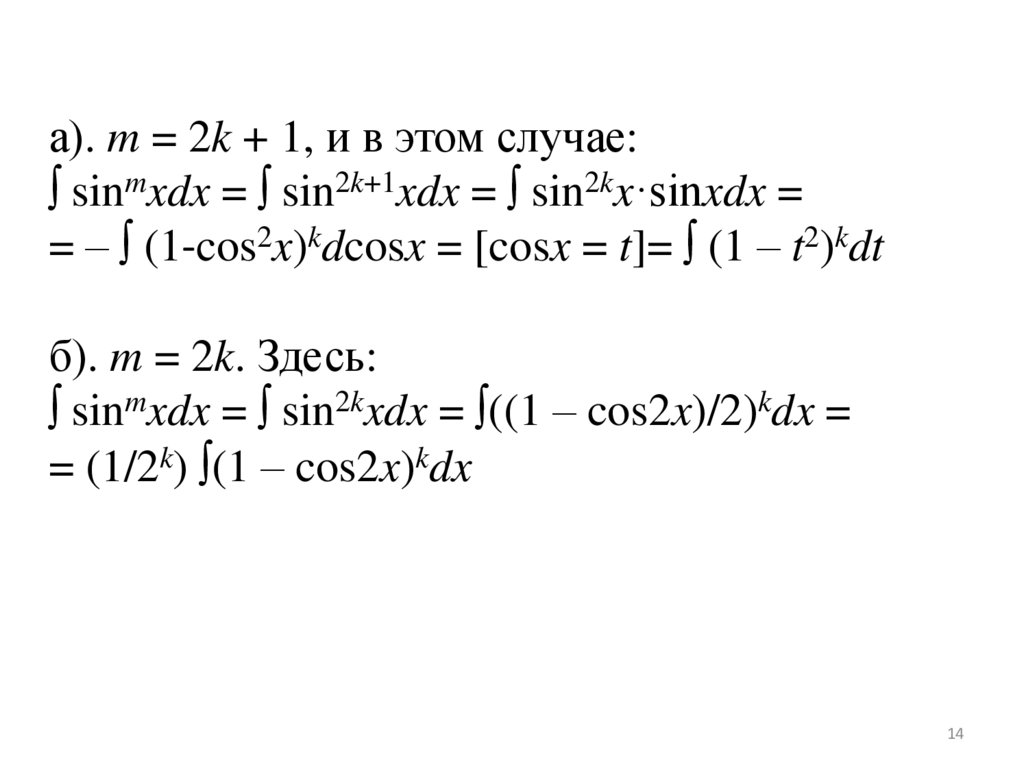


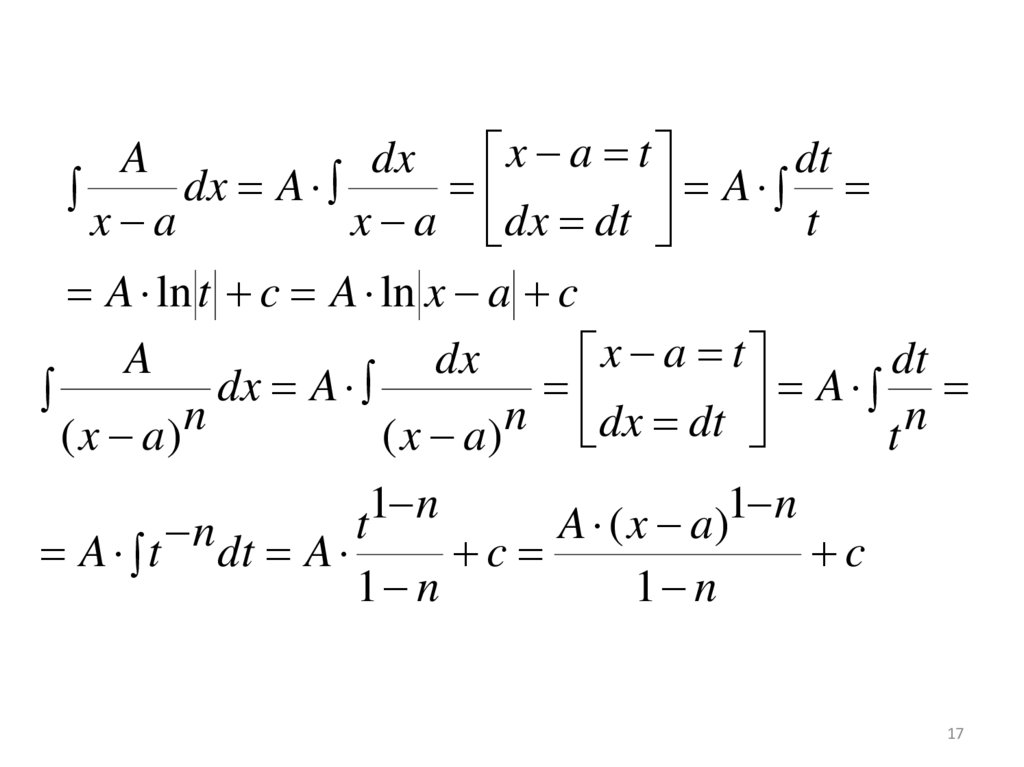

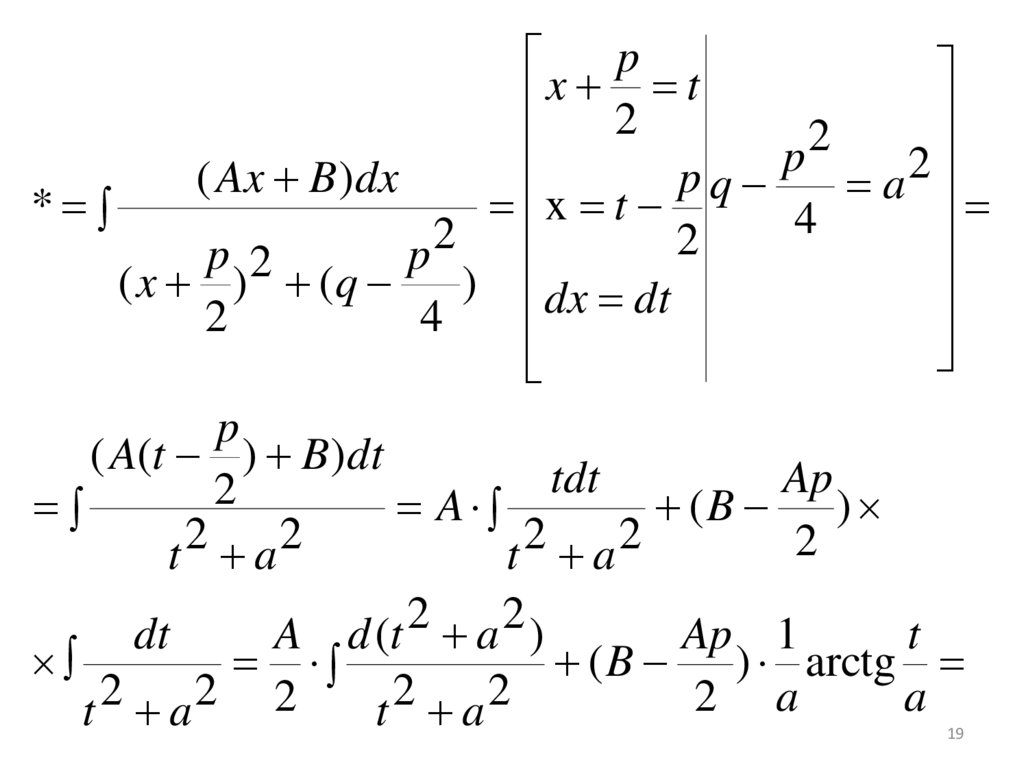
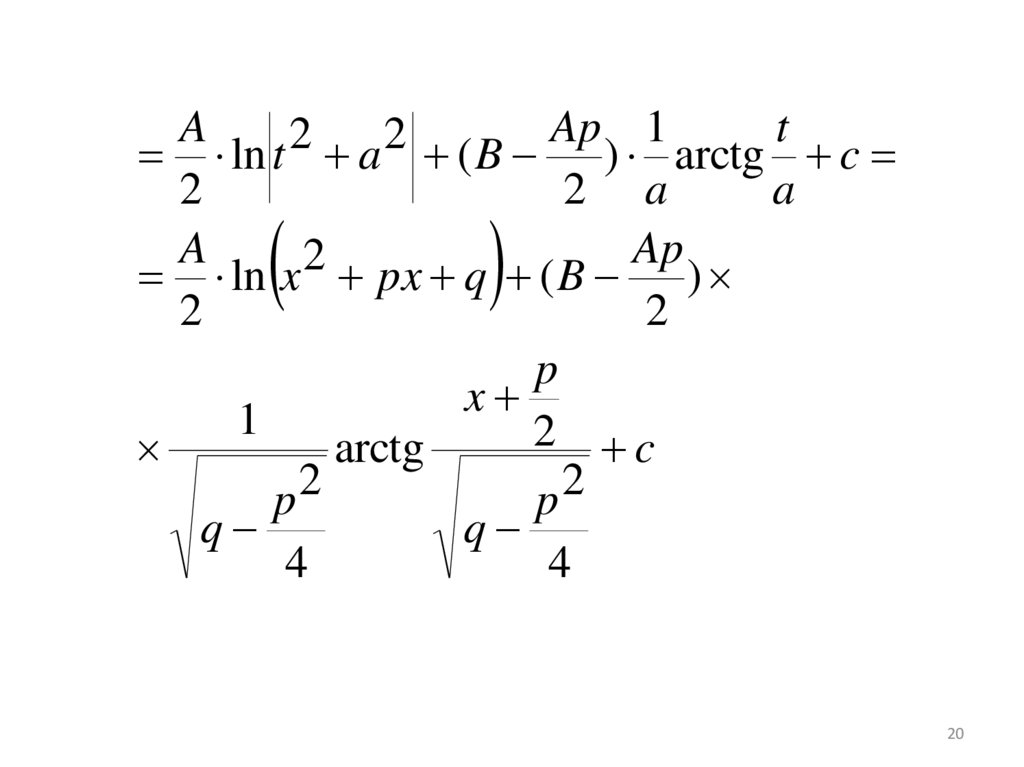

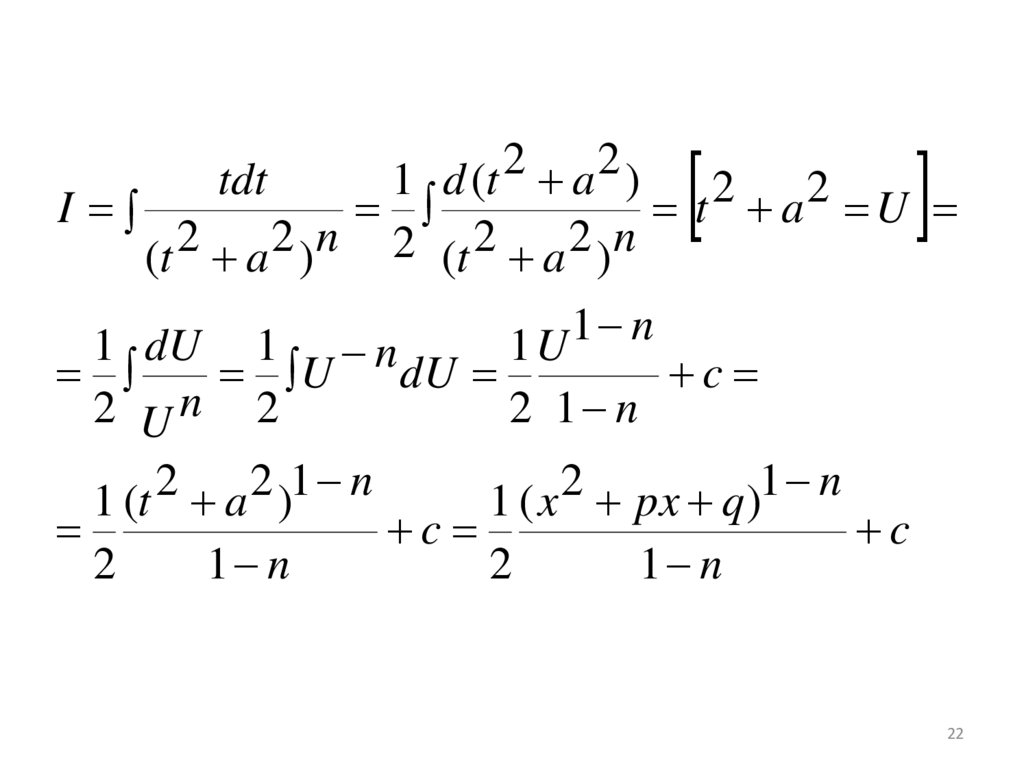
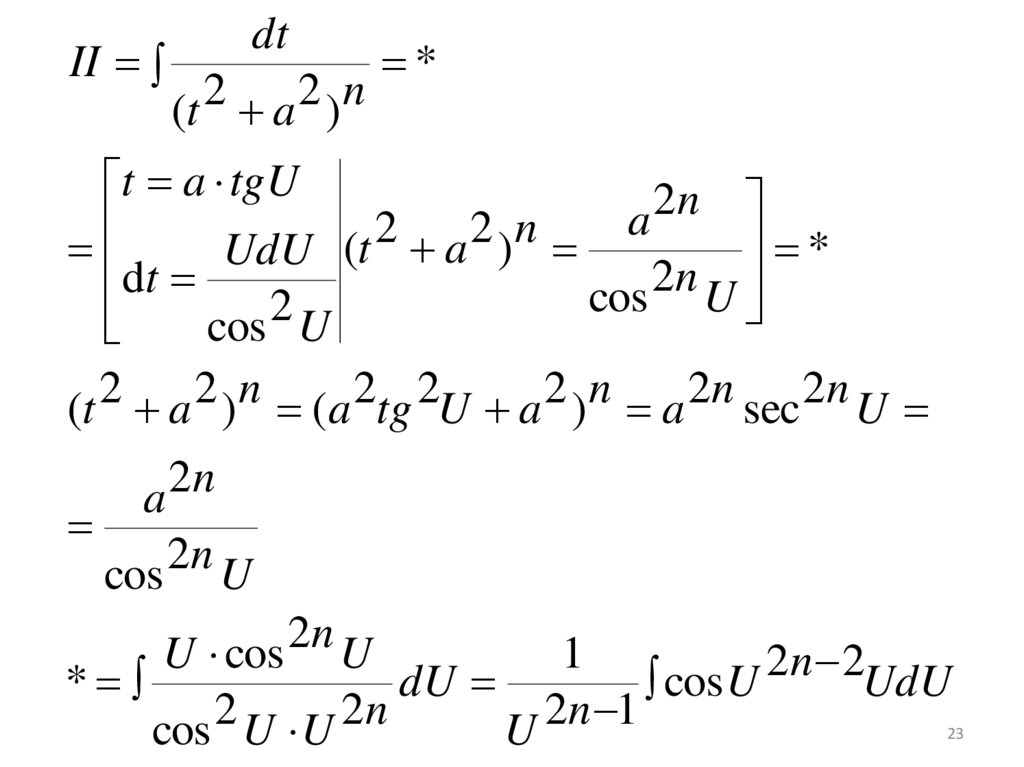




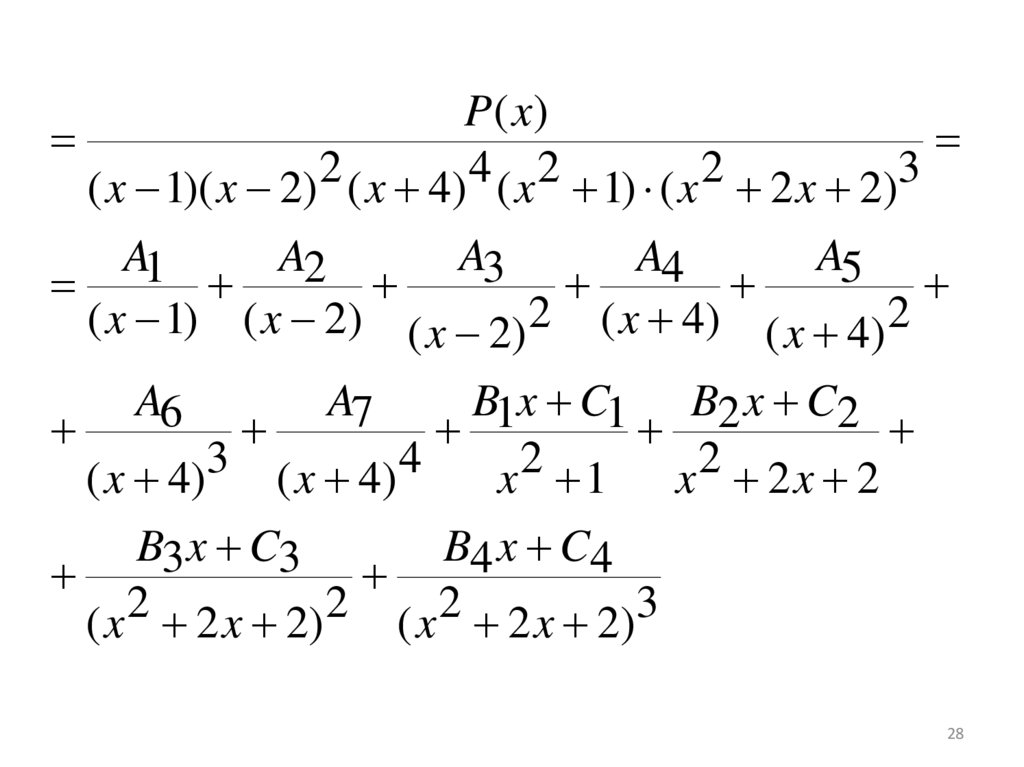
 mathematics
mathematics








