Similar presentations:
Основные методы интегрирования
1.
Первое высшее техническое учебное заведение РоссииСанкт-Петербургский горный университет императрицы
Екатерины II
Раздел: НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
Лекция 8
06.04.2025
ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
кафедра высшей математики
1/14
2.
1. Непосредственное интегрирование –через алгебраические преобразования и свойства НИ подвести к
табличным интегралам
ó dx = 1 ln 2 x + 3 + C
ô
2
õ 2x + 3
òe
х
х
ò sin 2 dx = -2 cos 2 + C
1
ò cos(3x + 1)dx = 3 sin(3x + 1) + C
-3 x
1 -3 x
dx = - e
+C
3
x
5+1
(
1
)
x
ó ( x - 1) 5 dx
6
6
ô
= ( - 1) + С
=
6
+
C
õ 6
6
5 +1
2/14
x
dx
d ( - 1) =
6
6
3.
2 (а). Замена переменной (метод подстановки)Пусть функция x = j (t ) определена и дифференцируема на отрезке [a , b ] и множество её
значений [a, b]. Тогда, если на отрезке [a, b] определена непрерывная функция f(x), для
которой существует первообразная, то на отрезке [a , b ] имеет место формула:
¢
[
]
f
(
x
)
dx
=
f
j
(
t
)
×
j
(
t
)
dt
.
x
=
j
(
t
)
ò
ò
Продифференцируем обе части равенства:
левая часть
¢
(ò f ( x)dx ) x = f ( x),
правая часть
(ò f [j (t )]j ¢(t )dt )x =
¢ dt = f [j (t )]j ¢(t ) 1 =
= (ò f [j (t )]j ¢(t )dt ) ×
j ¢(t )
dx
¢
t
= f [j (t )]= f ( x)
3/14
4.
2(б). Подведение под дифференциалd [f ( x)]= f ¢( x)dx
æ xö
dç ÷
èaø
ò
ó 1
ó
dx
dx
1 ô
dx
1ô a
= 2
=
2 = ô
2
2
2
ô
aô
a ô
æ xö
a +x
æ xö
õ 1+ ç ÷
ô 1+ ç ÷
õ
èaø
èaø
2
d ( x ) = 2 xdx
ó
æ xö
dç ÷
ô
1
è a ø = 1 arctg æ x ö + C
ô
ç ÷
2
aô
a
èaø
æ xö
ô 1+ ç ÷
õ
èaø
(
)
1 ó 2 xdx
ó xdx
1
1
1
du
2
ó
=
ô
=
ln
u
+
C
=
ln
1
+
x
+C
=
ô
2
ô
2
õ 1+ x
2 õ 1+ x
2
2
2õ u
(
d 1+ x
2
)= 2 xdx
(
1
xdx = d 1 + x 2
2
)
4/14
()
1
xdx = d x 2
2
5.
Пример 1. Найти интегралdx
ó
ô sin x
õ
x
= 2 ò sin x d
2
sin
x
sin
xd
(sin
x
)
ò
=
+C
2
( x ) = -2 cos x + c
2
t
ó
+C
ô tdt =
2
õ
ò d (sin x) = sin x + С
ó f ¢( x)dx ó d ( f ( x))
=ô
= ln f ( x) + C
ô
õ f ( x)
õ f ( x)
5/14
d
( x )= 2 x dx
1
dx
x
= 2d
( x)
6.
Пример 2. Найти интегралx
x = a sin t t = arcsin
a
p
p
–а х а
- £t £
2
2
2
2
ò a - x dx.
2
2
a -x =
2
2
2
a - a sin x = a cos t
dx = a cos tdt
2
а
2
2
2
2
2 ó 1 + cos 2t
dt =
ò (1 + cos 2t )dt =
a - x dx = a cos tdt = а ô
2
õ
2
2
а æ sin 2t ö
=
çt +
÷+C
вернёмся к старой переменной х:
2 è
2 ø
ò
ò
a2
sin 2t = a 2 sin t cos t = a sin t a 2 - (a sin t ) 2 = x a 2 - x 2 .
2
2
x
a
2
2
2
2
ò
x
a - x dx =
a -x +
arcsin + C.
2
2
a
6/14
7.
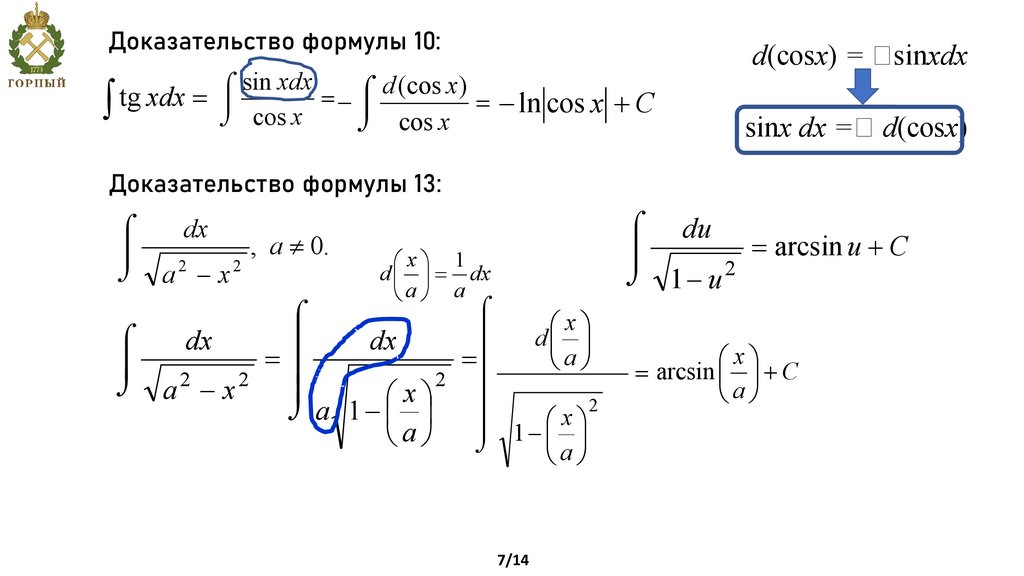
Доказательство формулы 10:ò
sin xdx
d
(cos
x
)
ó
ó
=- ô
tg xdx = ô
= - ln cos x + C
õ cos x
õ cos x
d(cosx) = sinxdx
sinx dx = d(cosx)
Доказательство формулы 13:
ó
ô
õ
dx
2
a -x
2
, a ¹ 0.
æ xö 1
d ç ÷ = dx
èaø a
ó
ó
æ xö
ô
dç ÷
ó
dx
dx
ô
=
=ô
èaø
ô
ô
2
2
2 ô
õ a -x
ô
æ xö
2
õ a 1- ç ÷ ô
æ xö
ô
è a ø õ 1- ç ÷
èaø
7/14
ó du
= arcsin u + C
ô
õ 1- u2
æ xö
= arcsin ç ÷ + C
èaø
8.
3. Интегрирование по частямЕсли функции u(x) и v(x) дифференцируемы на [ a, b] и существует
интеграл ∫v du, то на [ a, b] существует интеграл ∫u dv, причём
ò
ò
udv = uv - vdu.
По правилу дифференцирования произведения
d (uv) = vdu + udv Þ udv = d (uv) – vdu
Интеграл от каждого
слагаемого существует
8/14
9.
Методом интегрирования по частям найти интеграл:u = x,
du = dx
ò xe dx = dv = e dx, v = e x
x
x
u
dv
= xe x - ò e x dx = ( x - 1)e x + C
v du
Важно
x
x
du
=
e
dx
рационально
2
x
подбирать dv = xdx
v=
U и dV
2
1 2 x 1 x 2
ò xe dx = 2 x e - 2 ò e x dx
u=e
x
более сложный интеграл
u = x, du = dx
ì
ü
ò x cos xdx =íîdv = cos xdx, v = sin xýþ = x sin x - ò sin xdx
u dv
– cos x +C
= x sin x + cos x + C
9/14
10.
Интегрировать по частям удобно в интегралах:u
u
u
ax
P
(
x
)
cos
bxdx
,
P
(
x
)
sin
bxdx
,
P
(
x
)
e
dx
;
n
n
n
ò
ò
ò
Pn ( x) = a0 x + a1 x
n
n -1
+ ... + an -1 x + an .
Формулу применять n раз, понижая степень многочлена
Пример. Найти интеграл
2
u = x +1
( x 2 + 1) sin xdx =
ò
du = 2 xdx
dv = sin xdx v = - cos x
u=x
(
( )
= (1 - x )cos x + 2 x sin x + C
du = dx
)
= - x 2 + 1 cos x + 2 ò x cos xdx =
=
x
+
1
cos
x
+
(
)
2
x
sin
x
sin
xdx
=
ò
v
=
sin
x
dv = cos xdx
2
2
10/14
- cos x
11.
В интегралах:k
k
x
arctg
xdx
;
x
arcsin
xdx
;
ò
x
log
xdx
;
ò
ò
a
k
k
x
arcctg
xdx
.
x
arccos
xdx
;
ò
x
ln
xdx
;
ò
ò
за u следует принять трансцендентную функцию,
т.е. ln x, arcsin x, arctg x и т.п.
k
k
k +1
k
dv = x dx
x
v=
k +1
интеграл ∫v du не будет содержать
трансцендентной функции
11/14
12.
Пример. Найти интегралx
x
u
=
e
I = ò e sin xdx =
du = e dx
dv = sin xdx v = - cos x
x
x
u
=
e
du
=
e
dx
x
x
= -e cos x + ò e cos xdx =
dv = cos xdx v = sin x
x
= -e cos x + e sin x - ò e sin xdx
x
Имеем уравнение:
x
x
I = -e cos x + e sin x - I
x
x
x
e
(sin x - cos x )+ C
I=
2
12/14
13.
Вопросы:1. Какую замену сделать в интеграле?
ó 1+ 3 x
dx
ô
õ x +6 x
2
ó arctg x
dx
ô
2
õ 1+ x
t=6 x
ó sin x dx
ô
õ cos 3 x
2. Какую функцию принять за u в формуле интегрирования по частям
ò udv = uv - ò vdu
ò (x - 1)arccos xdx
u
(
)
x
1
cos
xdx
ò
u
3. Сколько раз следует применить формулу интегрирования по
3
частям в интеграле
ò (x - 1) cos xdx
13/14
u dv
ó x sin x dx
ô
õ cos 3 x
14.
Первое высшее техническое учебное заведение РоссииСанкт-Петербургский горный университет императрицы
Екатерины II
14/14










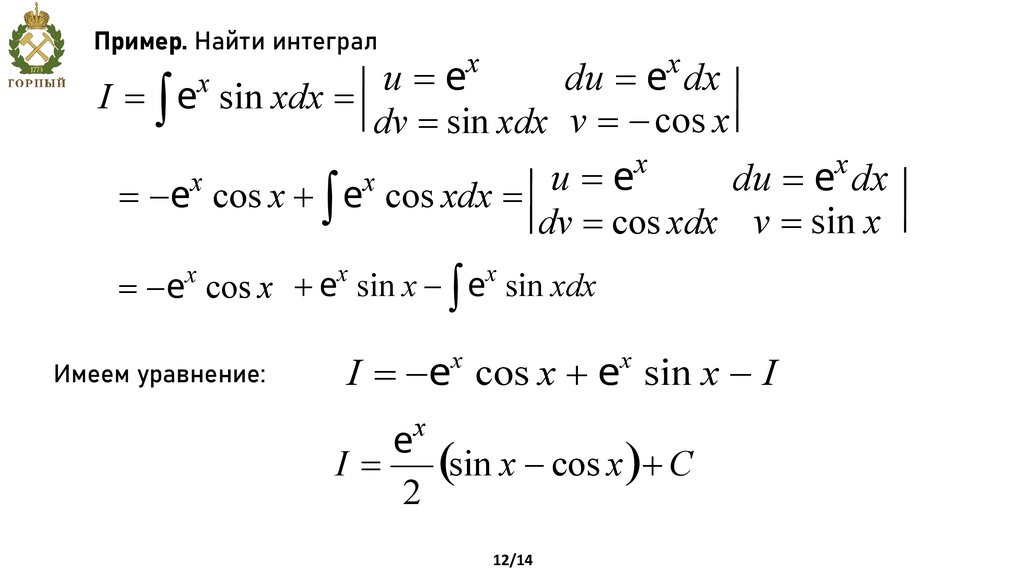


 mathematics
mathematics








