Семинар 9

1. Семинар 9

Краткое содержание
1. Электростатическое поле в диэлектрике
2. Граничные условия на границе раздела
двух однородных сред
3. Уравнение Пуассона
4. Расчет емкости простейших систем

2. Основные задачи электростатики

- получение соотношений,
связывающих геометрию проводников и диэлектриков,
распределение зарядов на поверхности проводников и в
разделяющих проводники диэлектриках с разностью
потенциалов между проводниками. Это практические задачи
расчета емкости систем заряженных проводников разной
конфигурации, максимальных напряженностей в изоляции и
максимально допустимого напряжения.
Интегральные уравнения расчета характеристик электростатического поля
при заданном распределении заряда, в однородной среде при наличии
симметрии поля (выбор поверхности, путь интегрирования)
q
E ds
S
0
2
(r ) Edr C
U12 1 2 Edr
1
скалярное произведение
E ds E ds cos( E ds) Edr E dr cos( E dr )
2

3. Системы координат

Решение задачи расчета характеристик поля зависит от выбора системы
координат. Выбор системы координат определяется наличием той или
иной пространственной симметрии, как задан источник поля (точечный
или распределенный заряд)
M iM x jM y kM z
M er M r e M e z M z M eR M R e M e z M z
Поле точечного заряда имеет центральную симметрию, решение в
сферической системе координат. Поле равномерно заряженного проводника
цилиндрической формы имеет осевую симметрию, решение в
цилиндрической системе координат. Для расчета поля плоского
конденсатора удобнее выбрать декартовую систему координат.
Плоскопараллельное поле может быть рассчитано в функциях двух
координат, так как решение поля одинаково для всех значений третьей
координаты. В более простых случаях характеристики поля могут быть
функцией одной координаты.
3

4. Основные задачи электростатики

.
Дифференциальные уравнения расчета характеристик
электростатического поля расчет характеристик поля в заданной точке
пространства (выбор системы координат)
В однородной среде ( r 0 =const) для потенциала справедливо
уравнение Пуассона:
divgrad
E grad
divgrad 0
уравнение Лапласа
- объемная плотность заряда [ Кл/м3 ] q dV
V
декартовая
2 2 2
2 2 2
x
y
z
grad i
j
k
x
y
z
1 1 2 2
1
r
grad er
e
ez
цилиндрическая
r r r r 2 2 z 2
r
r
z
4

5. Емкость системы проводящих тел

q
C
Емкость уединенного проводника
[Ф]
- потенциал проводника при условии, что 0
Емкость (конденсаторная емкость гальванической пары)
между двумя уединенными проводящими телами (системы
заряженных проводников) равна отношению:
C
q
1 2
1 2 - разность потенциалов проводников при условии
q1 q q2 q q1 q2 0
Для однородной двухпроводной линии (кабеля) длиной l
вводится емкость на единицу длины [Ф/м]:
C0
C
l
5

6. Вектор электрического смещения и вектор поляризации

Максвелл ввел специальную векторную характеристику - вектор
электрического смещения D [Кл/м2].
Постулат Максвелла
D ds q
св
S
В вакууме напряженность электрического поля электрическое смещение
связаны через электрическую постоянную: D 0 E .
Для поляризованного диэлектрика вводится вектор поляризации,
определяющий наличие связанных зарядов (диполей) P [Кл/м2].
P dS qсвяз .
s
Напряженность электрического поля для поляризованной среды
определяется и свободным и связанным зарядом.
S
(q q
E ds
св
связ
)
Для линейного диэлектрика P 0 ( r 1) E
0
D= 0 E P 0 r E
S
q
E ds
св
r 0
6

7. Граничные условия на границе раздела двух однородных диэлектриков

На границе раздела сред 1 и 2 с диэлектрическими проницаемостями 1 r1 0
и 2 r 2 0 :
1 2
1
1 2 где
1
2 2 где
n
n
E
D1n D2 n
E1 E2
1E1n 2 E2 n
На границе раздела двух поляризованных сред
P1n P2 n связ
P1n ( r1 1) 0 E1n
P2 n ( r 2 1) 0 E2 n
- поверхностная плотность заряда [ Кл/м2 ] q ds
На границе раздела диэлектрик-проводник
S
D2 n D1n св
Dn r 0 En
n
составляющая вектора электрического смещения,
нормальная к поверхности
7

8. Задача 1.

Плоский конденсатор с двумя слоями диэлектрика d1 = d2=1 см;
εrl = 3, εr2 = 6 зарядили до напряжения U = 100 В и отключили от
источника. Найти электрическое смещение, напряженность поля и
распределение потенциала в обоих диэлектриках.
y
D
ε1
Напряжение между пластинами конденсатора
(разность потенциалов):
ε2
n
x
U
d1 d 2
E ( x)dx E d E d
1 1
2 2
D1 x d D2 x d
0
D1 D2
d1
d2
n dx
1
r1 0 E1 r 2 0 E2
E1 66,7 В/см
100 0,01E1 0,01E2
E1 66,7 102 В/м
3E1 6E2
E2 33,3 102 В/м E2 33,3 В/см
En Ex E
D1 D2 =20000 0 0,1772 10 6 Кл/м 2
Dn Dx D
Потенциал: Edx C
D dx
E dx
1
(0) 100 B
(d1 d2 ) (0,02) 0
100 66,7 x 0 x 1
( x) x [см]
66,7 33,3x 1 x 2
d
8
Ex
dx

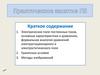
9. Задача 1 (продолжение).

Построим графики зависимости
E ( x) и ( x)
Построим графики зависимости E ( x )
D ( x) и P( x)
D1 0 E1 P1 [Кл/м2]
D2 0 E2 P2
E1 66,7 В/см
E2 33,3 В/см
100 66,7 x 0 x 1
( x) x [см]
66,7 33,3x 1 x 2
9

10. Задача 2.

Для задачи 1 определить: 1) как изменятся эти величины и емкость
конденсатора, если из конденсатора вынуть пластину второго
диэлектрика; 2) как изменятся эти величины и емкость конденсатора,
если конденсатор останется подключенным к источнику.
y
D
ε1
ε0
n
x
1 2
d1
D1 D2
d2
n dx
En Ex E
Dn Dx D
D dx
E dx
Емкость конденсатора определим на единицу поверхности:
C
q
C0
C
S U
U
6
2
На поверхности электродов D=20000 0 0,1772 10 Кл/м
0,1772 10 6
C0
1,772 10 9 Ф/м2
100
1) Если вынуть вторую пластину при отключенном источнике,
то останется неизменным заряд на пластинах, но изменится
напряженность во втором слое:
D
E2 200 В/см увеличится напряжение между пластинами
0
U E1d1 E2d2 266,7 B
0,1772 10 6
0,664 10 9 Ф/м2
Емкость уменьшится C0
266,7
10

11. Задача 2 (продолжение).

2) Если вынуть вторую пластину при включенном источнике,
то останется неизменным напряжение между пластинами и
изменятся напряженности в каждом слое:
y
D
ε1
ε0
n
x
1 2
D1 D2
100 0,01E1 0,01E2
E1 2500 В/м
3E1 1E2
E2 7500 В/м
Уменьшится поверхностный свободный заряд
d1
d2
n dx
En Ex E
Dn Dx D
D dx
E dx
D=7500 0 66,4 10 9 Кл/м2
Емкость уменьшится
66,4 10 9
C0
0,664 10 9 Ф/м 2
100
Дополнительное задание: построить графики зависимости
E ( x) , D ( x ) , P ( x) и ( x) для вариантов 1) и 2)
11

12. Задача 3.

В пространстве между заземленными электродами плоского воздушного
конденсатора распределен электрический заряд плотностью ρ, равной
ρ = ax. Координата x отсчитывается по нормали от одного из
электродов. Найти потенциал и напряженность поля. Расстояние между
электродами равно 2d. Построить распределение E ( x), ( x) , найти
потенциал изолированной металлической сетки, удаленной на
расстоянии от левой заземленной пластины. Пластина расположена
строго параллельно пластинам.
Дано: d= 0,1 м, а=5·10-4 Кл/м3, U=3 кВ, xC=6 см.
Решение: Уравнение Пуассона
d 2
ax
dx 2
0
0
d
ax 2
C1
dx
2 0
ax3
( x)
C1 x C2
6 0
Граничные условия (0) A 0
(d ) B U
12

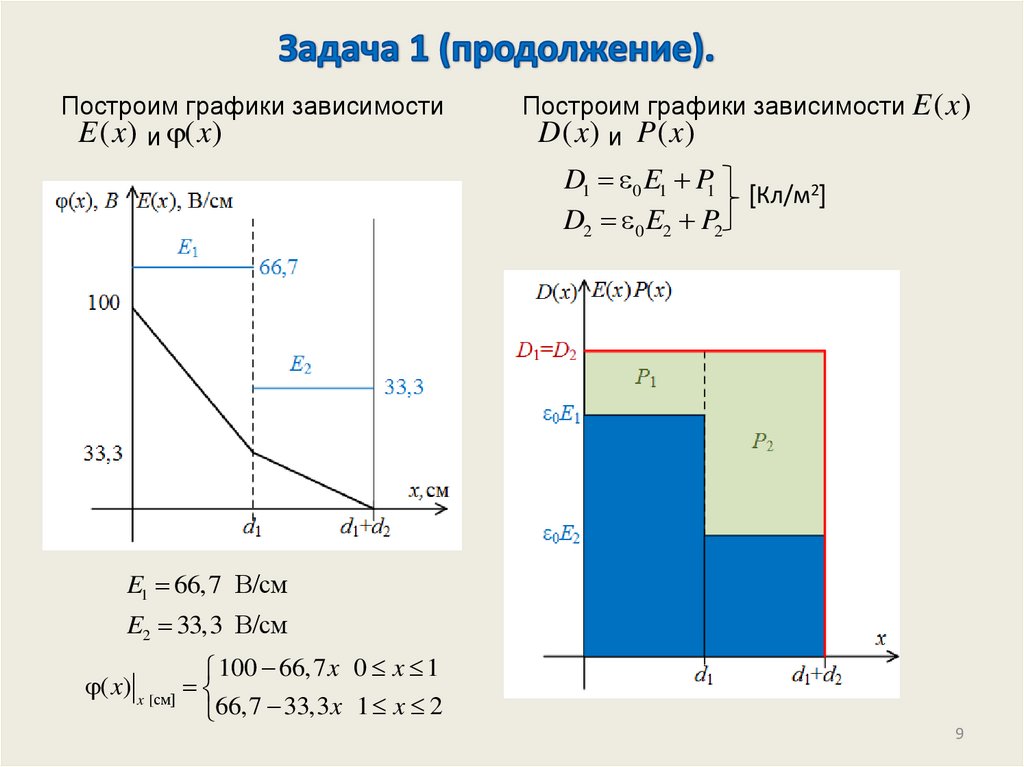
13. Задача 3 (продолжение).

ax3
( x)
C1 x C2
6 0
(0) A 0
(d ) B U
(0) C2 0
ad 3
(d )
C1d U
6 0
После подстановки численных
данных
( x) 9,4 106 x3 12,4 104 x, B
d
Ex ( x)
dx
E ( x) 28,2 10 x 12,4 10 , В/м
6
2
4
C ( xC ) 5410 B
13

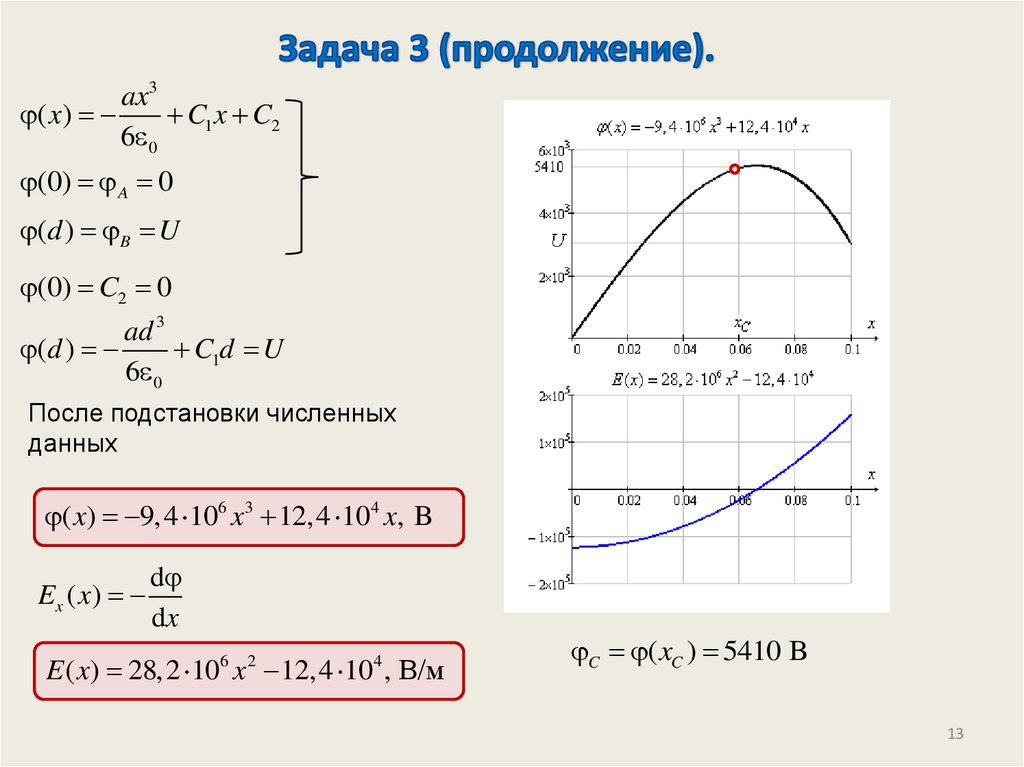
14. Задача 4.

Решить задачу 2 при условии, что сетка заземлена, а источник
изолирован.
Дано: d= 0,1 м, а=5·10-4 Кл/м3, U=3 кВ, xC=6 см.
Решение: Уравнение Пуассона и заданные
граничные условия
ax3
( x)
C1 x C2
6 0
(d ) (0) B A U
(0) A 5410 B
C ( xC ) 0
(d ) B 2410 B
( x) 9,4 106 x3 12,4 104 x 5410, B
Ex
d
dx
график не изменится
14

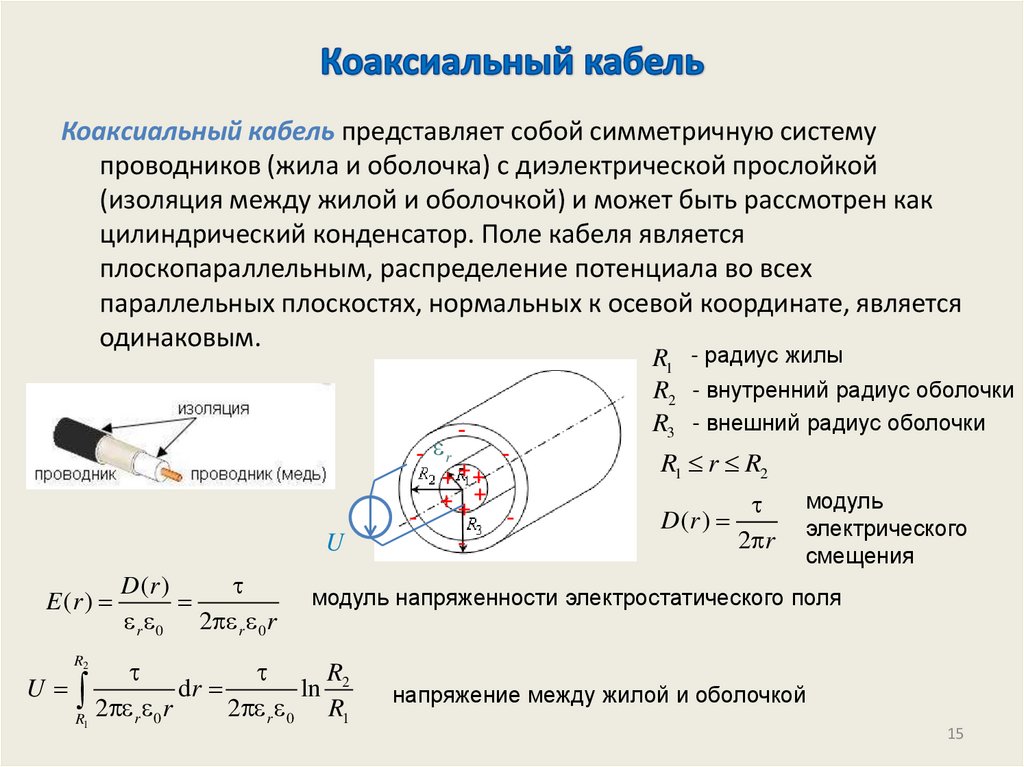
15. Коаксиальный кабель

представляет собой симметричную систему
проводников (жила и оболочка) с диэлектрической прослойкой
(изоляция между жилой и оболочкой) и может быть рассмотрен как
цилиндрический конденсатор. Поле кабеля является
плоскопараллельным, распределение потенциала во всех
параллельных плоскостях, нормальных к осевой координате, является
одинаковым.
-
U
E (r )
D(r )
r 0 2 r 0 r
- r
+
+ +
+ ++
-
R1 - радиус жилы
R2 - внутренний радиус оболочки
R3 - внешний радиус оболочки
R1 r R2
D(r )
2 r
модуль
электрического
смещения
модуль напряженности электростатического поля
R
dr
ln 2
2 r 0 r
2 r 0 R1
R1
R2
U
напряжение между жилой и оболочкой
15

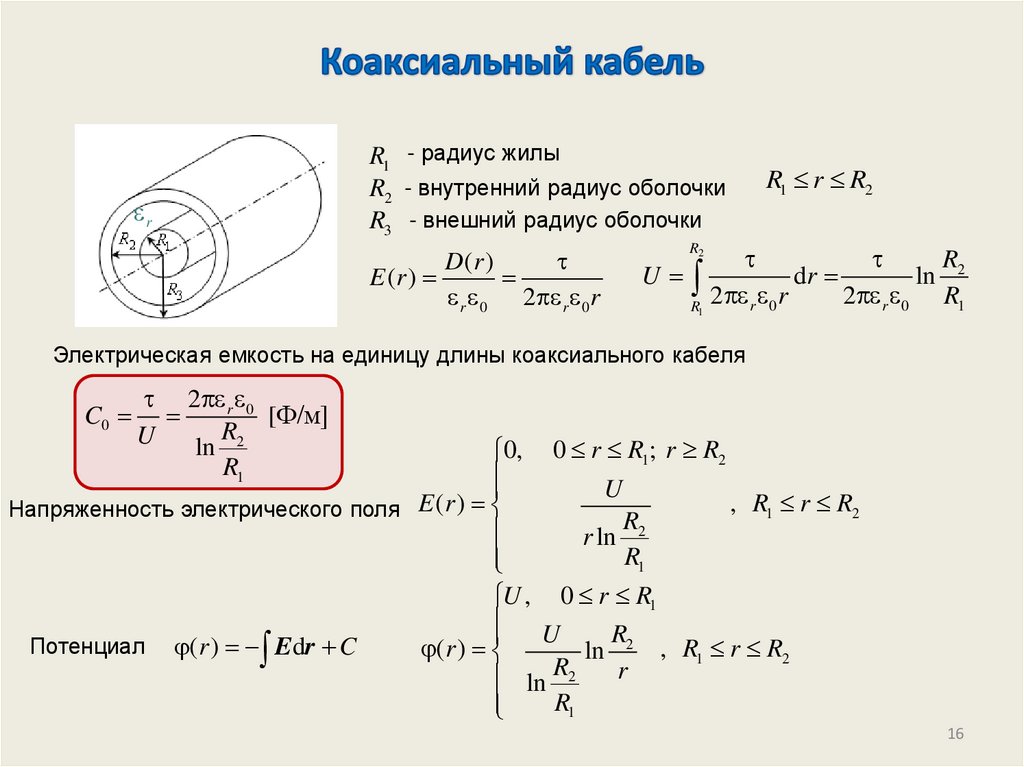
16. Коаксиальный кабель

r
R1 - радиус жилы
R2 - внутренний радиус оболочки
R3 - внешний радиус оболочки
D(r )
E (r )
r 0 2 r 0 r
R1 r R2
R
dr
ln 2
2 r 0 r
2 r 0 R1
R1
R2
U
Электрическая емкость на единицу длины коаксиального кабеля
C0
2 r 0
[Ф/м]
R2
U
ln
R1
0, 0 r R1; r R2
U
, R1 r R2
Напряженность электрического поля E (r )
R
r ln 2
R1
U , 0 r R1
U
R
Потенциал (r ) Edr C
(r )
ln 2 , R1 r R2
r
ln R2
R1
16

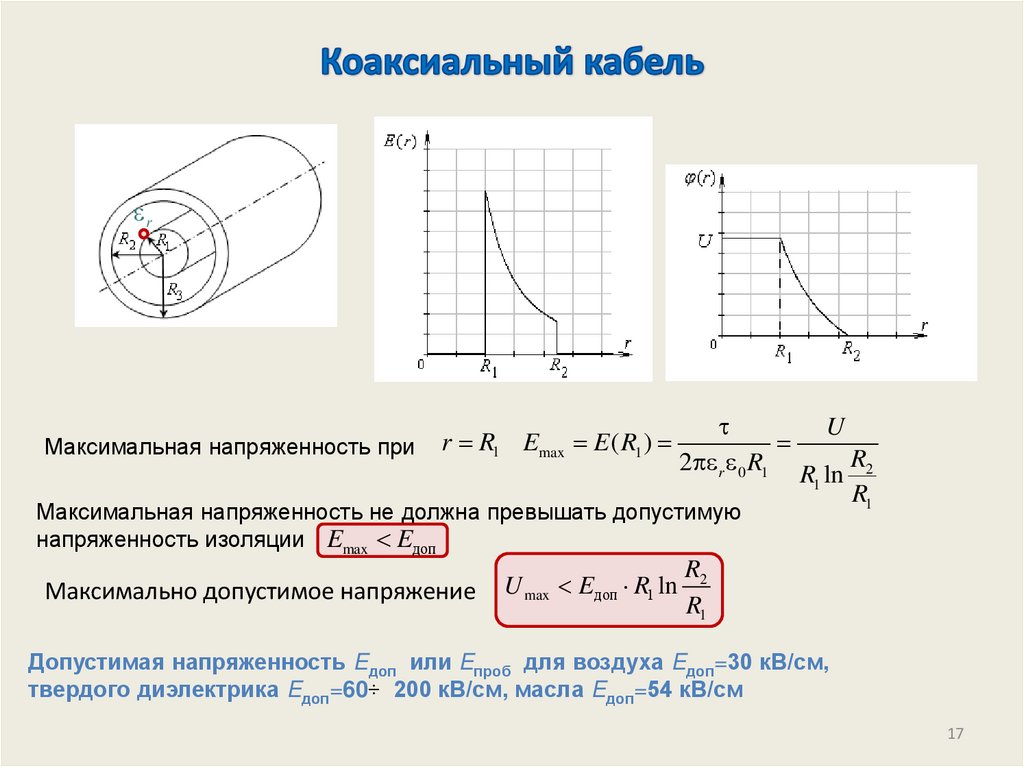
17. Коаксиальный кабель

r
Максимальная напряженность при
r R1 Emax E ( R1 )
U
2 r 0 R1 R ln R2
1
R1
Максимальная напряженность не должна превышать допустимую
напряженность изоляции Emax Eдоп
Максимально допустимое напряжение
U max Eдоп R1 ln
R2
R1
Допустимая напряженность Eдоп или Eпроб для воздуха Eдоп=30 кВ/см,
твердого диэлектрика Eдоп=60 200 кВ/см, масла Eдоп=54 кВ/см
17

18. Задача 5.

К цилиндрическому конденсатору дважды подводится напряжение, доводящее
конденсатор до пробоя: первый раз, когда диэлектриком был воздух,
пробивная напряженность которого Епр = E1 =30 кВ/см, и второй раз, когда
диэлектриком было масло (εr = 2,4) с Епр = Е2 = 54 кВ/см.
Определить соотношение между напряжениями, прикладываемыми к
конденсатору в первом и во втором случаях, и между зарядами конденсаторов
в тех же случаях.
Решение: Максимальная напряженность при r R1
Emax
U доп
max
,
2 r 0 R1 R1 ln( R2 / R1 )
максимальная линейная плотность заряда
max 2 r 0 R1Eпр
Отношение допустимых напряжений равно отношению
пробивных напряженностей
U1доп E1
0,556
U 2доп E2
1max r1E1
0, 232
Отношение максимальных плотностей зарядов
E
2max
r2 2
18

19. Задача 6.

Двухслойный цилиндрический конденсатор (R1 = 1 мм, R2 =2 мм, R3 = 4 мм)
заполнен двухслойным диэлектриком: 1) εra = 1; εrb = 3 или 2) εra = 3; εrb = 1.
Определить в обоих случаях пробивное напряжение и построить зависимости
модуля напряженности E (r ) . Пробивная напряженность воздуха 30 кВ/см,
пробивная напряженность диэлектрика 60 кВ/см.
Решение: Напряженность в первом и втором слоях
R1
R3
ra
rb
2 ra 0 r
Eb (r )
2 rb 0 r
Ea (r )
R2
R1 r R2
R2 r R3
ra Ea r R rb Eb r R
R3
Напряжение между жилой и оболочкой U E (r )dr
R1
2
2
R3
1
R2 1
ln
ln
.
2 0 ra R1 rb R2
Максимальная напряженность первого слоя при r R1
Максимальная напряженность второго слоя при r R2
Ea max Ea r R
1
a max
2 ra 0 R1
Eb max Eb r R
2
b max
2 rb 0 R2
19

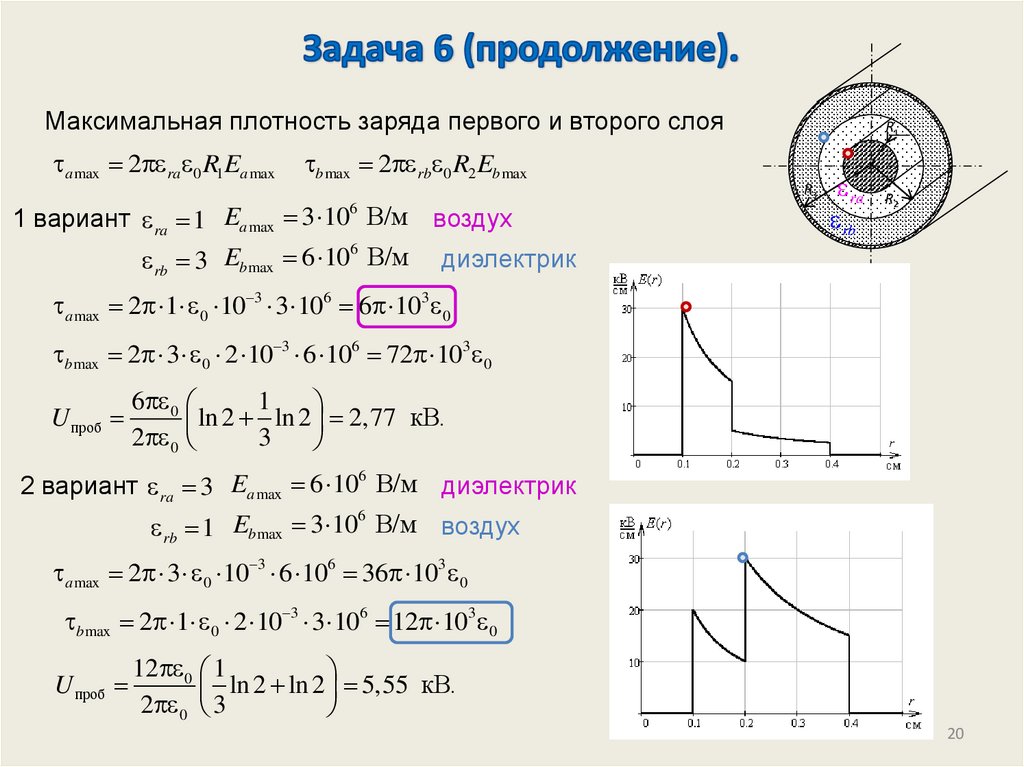
20. Задача 6 (продолжение).

Максимальная плотность заряда первого и второго слоя
a max 2 ra 0 R1Ea max
R1
b max 2 rb 0 R2 Eb max
1 вариант ra 1 Ea max 3 10 В/м воздух
6
rb 3 Eb max 6 10 В/м диэлектрик
6
R3
ra
rb
R2
a max 2 1 0 10 3 3 106 6 103 0
b max 2 3 0 2 10 3 6 106 72 103 0
U проб
6 0
1
ln
2
ln
2
2,77 кВ.
2 0
3
2 вариант ra 3 Ea max 6 10 В/м диэлектрик
6
rb 1 Eb max 3 10 В/м воздух
6
a max 2 3 0 10 3 6 106 36 103 0
b max 2 1 0 2 10 3 3 106 12 103 0
U проб
12 0 1
ln 2 ln 2 5,55 кВ.
2 0 3
20

21.

Автор доц. каф. ТОЭ НИУ «МЭИ»
Жохова М.П.
ZhokhovaMP@mpei.ru
21