конденсаторы 21 ИКС

1.

Конденсатор.
Типы конденсаторов.
Конденсаторные цепи.

2.

Электроемкость уединенного проводника
Уединенный проводник - это проводник, который находится
далеко от других тел так, что влиянием их электрических
полей можно пренебречь.
q+
q
q
+
+
+
Потенциал уединенного проводника
пропорционален находящемуся на нем
заряду: q ~ φ
q C
Электроемкость – это коэффициент пропорциональности,
физическая величина, характеризующая способность
проводника или системы проводников накапливать
электрические заряды.
С
Единица электроемкости - фарад (Ф)
1 нФ (нанофарад) = 10-9 Ф
1 пФ (пикофарад) = 10-12 Ф
q

3.

Конденсаторы
Рассчитать электроемкость уединенного проводника,
имеющего форму сферы радиуса R.
Задача 1:
Между разностью потенциалов и напряженностью поля существует
соотношение
r
E r
1 2 Edr
E
2
r
1
q
E
2
4 0 r
φ
ε R
r1 R
r2
2 0
r1
1
q
1
dr
2
4 0 r
К
q 1
q
4 0 r R
4 0 R
Электроемкость: С
q
C 4 0 R
Электроемкость зависит:
- от геометрии проводника,
- от относительной диэлектрической проницаемости среды.

4.

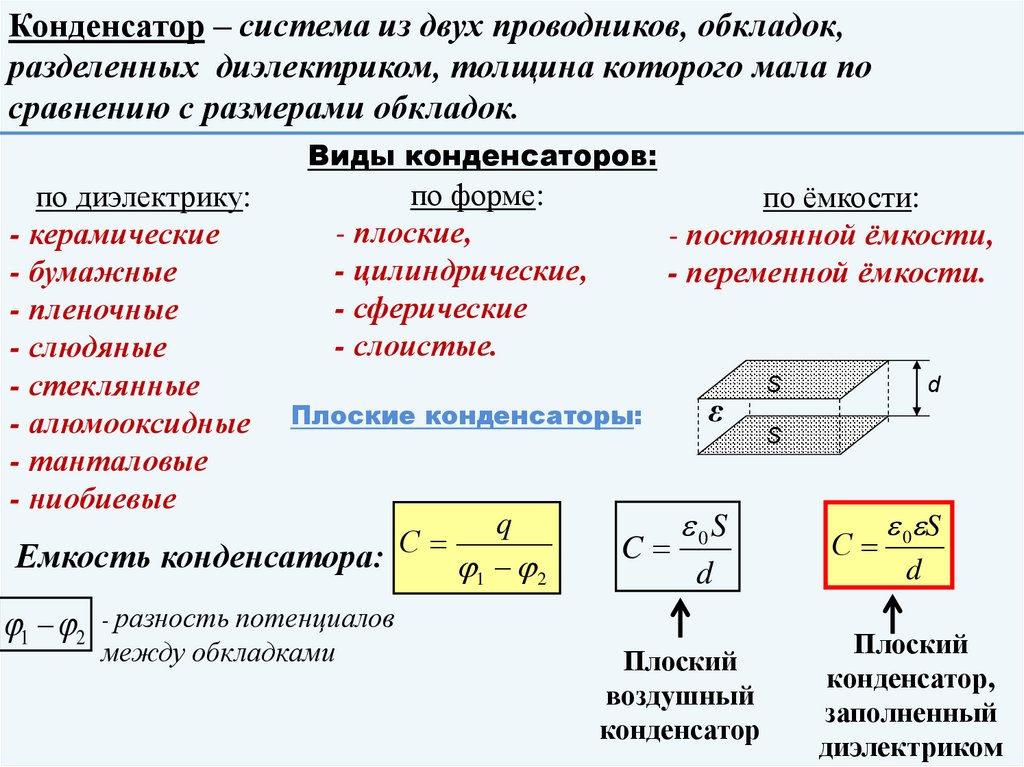
Конденсатор – система из двух проводников, обкладок,
разделенных диэлектриком, толщина которого мала по
сравнению с размерами обкладок.
Виды конденсаторов:
по диэлектрику:
- керамические
- бумажные
- пленочные
- слюдяные
- стеклянные
- алюмооксидные
- танталовые
- ниобиевые
по форме:
- плоские,
- цилиндрические,
- сферические
- слоистые.
по ёмкости:
- постоянной ёмкости,
- переменной ёмкости.
Плоские конденсаторы:
q
Емкость конденсатора: С
1
2
1 2 - разность потенциалов
между обкладками
C
ε
0S
d
Плоский
воздушный
конденсатор
S
d
S
С
0 S
d
Плоский
конденсатор,
заполненный
диэлектриком

5.

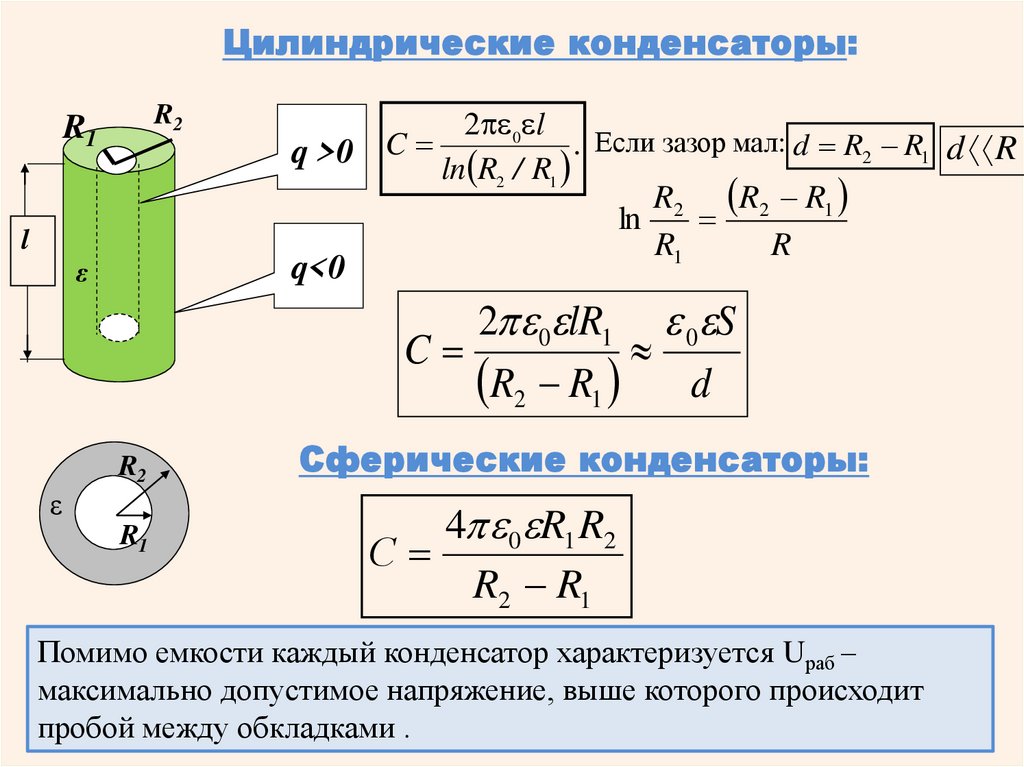
Цилиндрические конденсаторы:
R2
R1
q >0
l
q<0
ε
2 0 l
C
. Если зазор мал: d R2 R1 d R
ln R2 / R1
R2 R2 R1
ln
R1
R
2 0 lR1 0 S
C
R2 R1 d
R2
ε
R1
Сферические конденсаторы:
4 0 R1 R2
С
R2 R1
Помимо емкости каждый конденсатор характеризуется Uраб –
максимально допустимое напряжение, выше которого происходит
пробой между обкладками .

6.

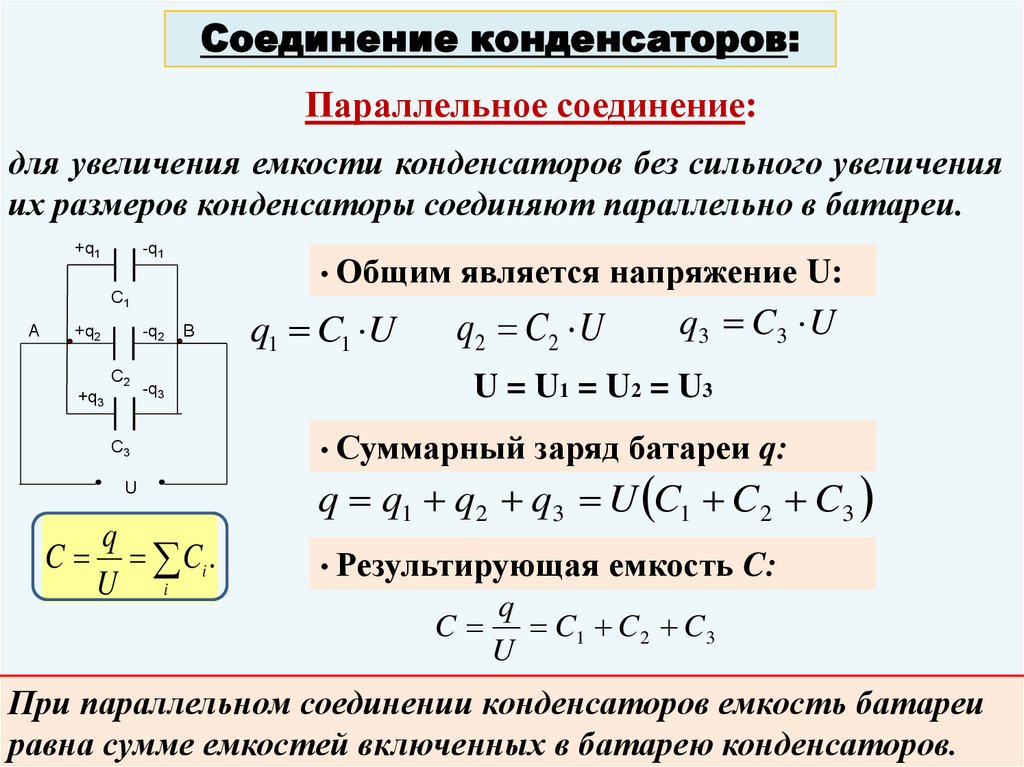
Соединение конденсаторов:
Параллельное соединение:
для увеличения емкости конденсаторов без сильного увеличения
их размеров конденсаторы соединяют параллельно в батареи.
+q1
-q1
• Общим является напряжение U:
С1
A
+q2
-q2
С2
+q3
B
-q3
С3
U
q
C Ci .
U i
q1 C1 U
q2 C2 U
q3 C3 U
U = U1 = U2 = U3
• Суммарный заряд батареи q:
q q1 q2 q3 U C1 C 2 C3
• Результирующая емкость C:
C
q
C1 C 2 C3
U
При параллельном соединении конденсаторов емкость батареи
равна сумме емкостей включенных в батарею конденсаторов.

7.

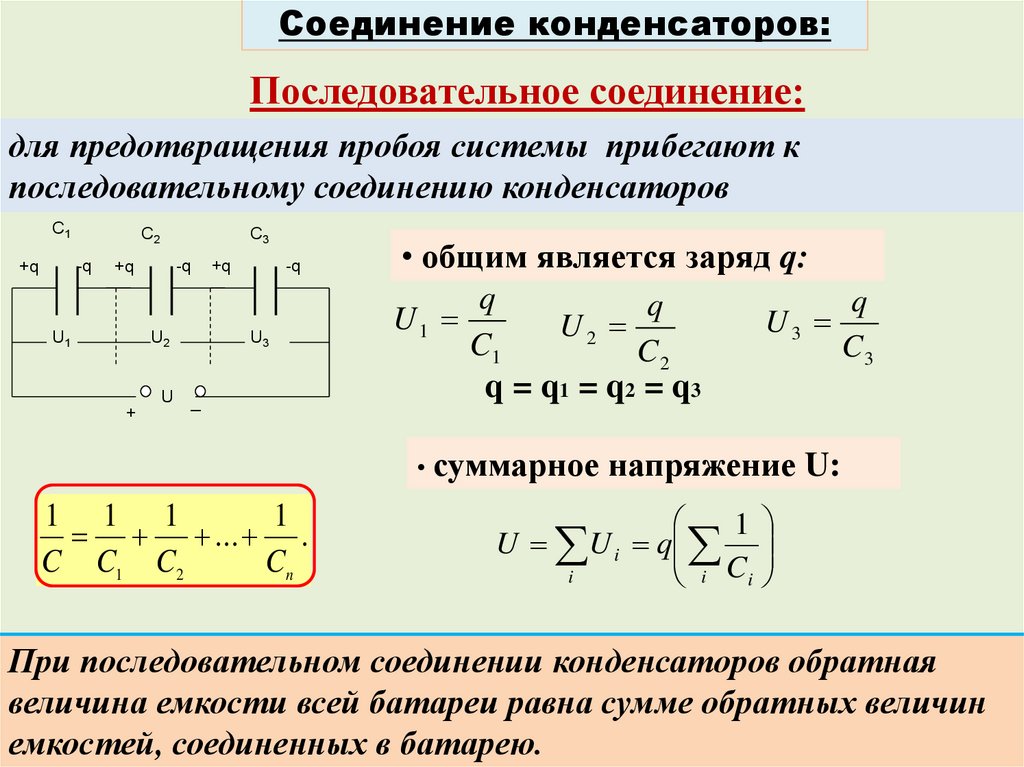
Соединение конденсаторов:
Последовательное соединение:
для предотвращения пробоя системы прибегают к
последовательному соединению конденсаторов
С1
С2
-q
+q
С3
-q
+q
U2
U1
U
+
+q
-q
U3
_
• общим является заряд q:
q
q
q
U1
U3
U2
C1
C3
C2
q = q1 = q2 = q3
• суммарное напряжение U:
1 1 1
1
... .
C C1 C2
Cn
1
U U i q
i
i Ci
При последовательном соединении конденсаторов обратная
величина емкости всей батареи равна сумме обратных величин
емкостей, соединенных в батарею.

8. Последовательно-параллельное соединение конденсаторов - это цепь имеющая в своем составе участки, как с параллельным, так и с

Последовательно-параллельное соединение конденсаторов это цепь имеющая в своем составе участки, как с
параллельным, так и с последовательным соединением
конденсаторов.
При расчете общей емкости такого участка
цепи этот участок разбивают на
простейшие участки.
Алгоритм расчета:
1. Определить эквивалентную емкость
участков с параллельным соединением
конденсаторов.
2. Если эти участки содержат
последовательно соединенные конденсаторы,
то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей
конденсаторов перерисовывают схему.
Обычно получается цепь из последовательно
соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.

9.

Конденсаторы
Соединение конденсаторов
Высоковольтный импульсный генератор
Если n одинаковых конденсаторов электроемкостью С каждый
соединить параллельно и зарядить до разности потенциалов Δφ ,
а
затем в заряженном состоянии соединить их последовательно, то на
зажимах батареи появится разность потенциалов nΔφ
С
С
С
С
а)
n
С
С
б )
С
С

10.

ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА
+q
Если замкнуть обкладки заряженного конденсатора, то по
проволоке, соединяющей эти обкладки, потечет ток, Сила
тока может достигать такой величины, что проволока
расплавится. Следовательно, можно сделать вывод о том,
что есть энергия.
-q
Пусть конденсатор заряжен до напряжения U, U мгновенное значение напряжения при разрядке конденсатора. Если
при этом значении напряжения протечет заряд dq, то работа dA dW
dA U dq
c
dq CdU dA CU dU
. Полная энергия при разрядке конденсатора от U до 0:
CU 2
WC dA CU dU
.
2
U
0
0
U
Энергию конденcатора можно
выразить через заряд q:
CU 2
W
2
q2
WC ;
2C
1
WC qU .
2

11.

Энергия электростатического поля
Энергию заряженного конденсатора можно выразить через
величины, характеризующие электрическое поле в зазоре между
обкладками. Сделаем это на примере плоского конденсатора.
С
WC
w
0 S
CU 2
WC
2
d
0 S d U 2
2
W
V
d
2
WC
0 SU 2
2d
U
2
E
d2
Объемная плотность
энергии
E 0E D
w
2
WC
2
S d V
Умножим и разделим на d
w
0 E 2
0 E 2V
2 V
2
V
0 E 2
2
DE
2
2
E
EP
w 0
2
2
Первое слагаемое в этом выражении совпадает с плотностью энергии поля Е в вакууме
Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика.

12.

Итак, заряженный конденсатор обладает энергией.
q2
WC
2C
WC
0 E 2
2
V
Одна формула связывает энергию конденсатора с зарядом на его
обкладках, Другая формула - с напряженностью поля.
Логично поставить вопрос: где же локализована (сосредоточена)
энергия, что является носителем энергии – заряды или поле?
В пределах электростатики ответ на этот вопрос дать
невозможно: поля и заряды, их образовавшие, не могут
существовать обособленно. Однако переменные поля могут
существовать независимо от возбудивших их зарядов (излучение
Солнца, радиоволны и т.д.) и они переносят энергию. Эти факты
говорят о том, что носителем энергии является поле.

13.

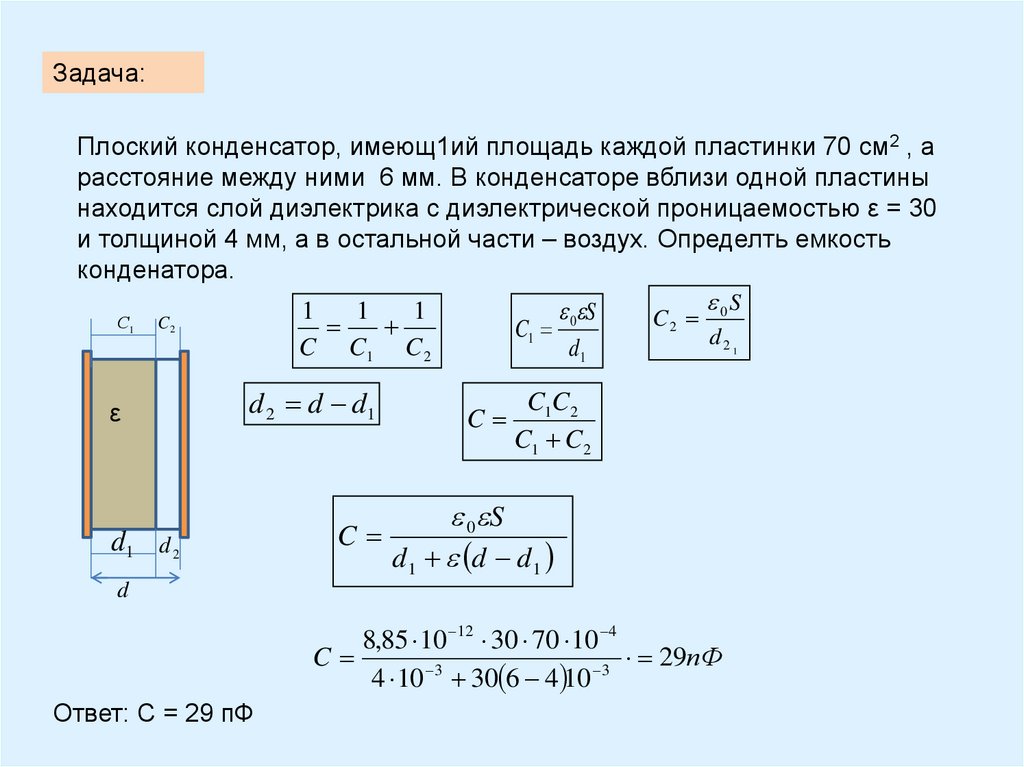
Задача:
Плоский конденсатор, имеющ1ий площадь каждой пластинки 70 см2 , а
расстояние между ними 6 мм. В конденсаторе вблизи одной пластины
находится слой диэлектрика с диэлектрической проницаемостью ε = 30
и толщиной 4 мм, а в остальной части – воздух. Определть емкость
конденатора.
0S
1
1
1
0 S
C
С1 C2
2
C1
d2
C C1 C 2
d1
1
ε
d 2 d d1
d1 d 2
C
C
C1C2
C1 C 2
0 S
d1 d d1
d
8,85 10 12 30 70 10 4
C
29пФ
3
3
4 10 30 6 4 10
Ответ: С = 29 пФ

14.

Задача 3:
В некоторой точке диэлектрика с относительной диэлектрической
проницаемостью ε = 20, электрическое смещение имеет значение
D = 600 нКл/м². Чему равна поляризованность в этой точке
диэлектрика?
Дано:
Решение.
ε = 20 ;
Между электрическим смешением и поляризованностью
D = 600 нКл/м²
диэлектрика существует связь:
D
Найти:
P D 0 E E
D 0 E P
0
P-?
P D 0
D
1
D 1
0
1 P 600 20 1 570
P D
20
Выразим напряженность поля через смещение :
.
Ответ:570 нКл/м².

15.

Задача 4:
Площадь пластин плоского воздушного конденсатора равна 10-2 м2,
расстояние между ними 5 мм. До какой разности потенциалов был
заряжен конденсатор, если при его разрядке выделилось 4,2·10-3 Дж
энергии?
Дано:
S=10-2 м2
d=5 мм=5·10-3м
ε=1
ε0=8,85·10-12Ф/м
W=4,2·10-3 Дж
U-?
Решение:
2
C
S
0
d
U 2W
W CU
C
2
1 8,85 10 Фм 10 м
1,77 10 Ф
C
5 10 м
12
2
2
11
3
Дж
2
4
,
2
10
2,2 10 В
U
1,77 10 Ф
3
4
11
Ответ: U 2,2 10 В
4

16.

Задача 5:
Три конденсатора соединены между собой параллельно. Емкость
первого равна 100 мкФ, второго — 200 мкФ, третьего — 500 мкФ.
Найдите общую емкость конденсаторов.
Домашнее задание:
1. Вычислите ёмкость батареи, состоящей из
3 конденсаторов, ёмкостью 1 мкФ, при
всех возможных случаях их соединения.