Проводники в электростатическом поле. Конденсаторы. Энергия электрического поля

1. Лекция 4

Проводники в
электростатическом поле.
Конденсаторы.
Энергия электрического поля.

2.

1.16. Равновесное распределение зарядов на проводниках.
1.17. Электроемкость проводников. Конденсаторы.
1.18. Вычисление емкости простых конденсаторов.
1.19. Соединение конденсаторов.
1.20. Энергия системы неподвижных точечных зарядов.
1.21. Энергия заряженного проводника и заряженного
конденсатора.
1.22. Энергия электростатического поля.

3. 1.16. Равновесное распределение зарядов на проводниках

Опыт показывает, что при равновесии электрические заряды распределяются на
внешней поверхности проводников. Поэтому,
согласно теореме Гаусса,
электрическое поле внутри проводника Е 0 , а потенциал φ = const.
Из сказанного следует, что при равновесии зарядов поверхность проводника
является эквипотенциальной. Вблизи поверхности заряженного проводника
силовые линии перпендикулярны его поверхности, и поэтому работа по
перемещению заряда вдоль любой линии на поверхности проводника
A q( 1 2 ) 0 .
При внесении незаряженного проводника в электрическое поле на его внешней
поверхности появляются индукционные заряды противоположного знака,
электрическое поле которых компенсирует внутри проводника внешнее поле.
На этом свойстве проводников основано действие электростатической
защиты.

4. 1.17. Электроемкость проводников. Конденсаторы.

Заряд q, сообщенный уединенному проводнику создает
вокруг него электрическое поле, напряженность которого
пропорциональна величине заряда. Потенциал поля φ, в
свою очередь, связан с напряженностью поля также
пропорциональной зависимостью. Следовательно, заряд и
потенциал уединенного проводника связаны между собой
линейной зависимостью:
q = Cφ
Коэффициент
пропорциональности
С
называется
электроемкостью (или просто емкостью) проводника.
Емкость проводника зависит от его формы и размеров, а
также свойств окружающей проводник среды. Если
проводник находится в непроводящей среде с
диэлектрической проницаемостью ε, то его емкость
увеличивается в ε раз.

5.

Единицы измерения электроемкости в СИ:
С q Кл Ф
В
3 10 9 СГСЭq
1Ф
9 1011 см 9 10 6 км
1
СГСЭ
300
1мкФ 10 6 Ф
1нФ 10 9 Ф
1пФ 10 12 Ф
Пара проводников, между которыми имеется разность
потенциалов, называется простейшим конденсатором.
Индуцированные на проводниках заряды равны по
величине и противоположны по знаку. Заряд каждой
пластины по абсолютной величине q С( 1 2 ) СU
Если пространство между проводниками заполнено средой с
диэлектрической проницаемостью ε, то С С0
где С0 - емкость конденсатора в вакууме.

6. 1.18. Вычисление емкости простых конденсаторов.

Согласно определению, емкость конденсатора:
2
q
U
(
E
d
r
)
С
1
2
, где
U
1
(интеграл берется вдоль силовой линии поля между обкладками
конденсатора).
Следовательно, общая формула для вычисления емкости любого
конденсатора есть:
q
С 2
( Edr )
1
Рассмотрим ряд примеров на применение этой формулы.

7.

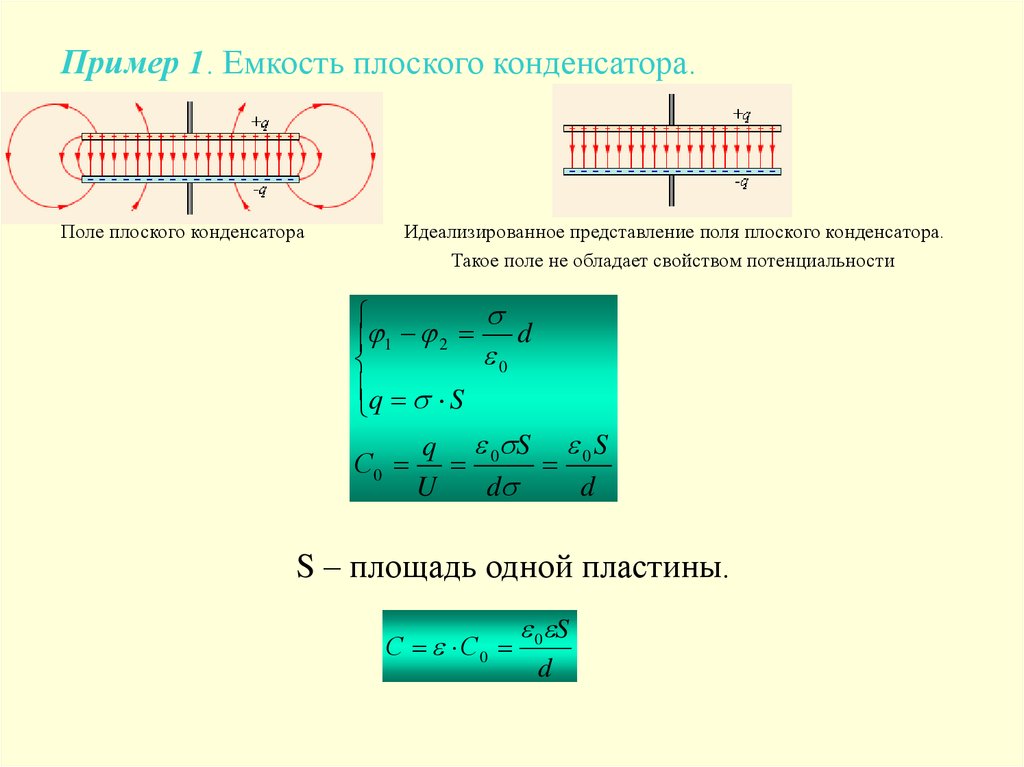
Пример 1. Емкость плоского конденсатора.
Поле плоского конденсатора
Идеализированное представление поля плоского конденсатора.
Такое поле не обладает свойством потенциальности
d
1
2
0
q S
q 0 S 0 S
С0
U
d
d
S – площадь одной пластины.
С С0
0 S
d

8.

Пример 2. Емкость цилиндрического конденсатора
Цилиндрический конденсатор – система из двух соосных
с
проводящих цилиндров радиусов r1 и r2 и длины l .
Емкости этих конденсаторов, заполненных диэлектриком
диэлектрической проницаемостью ε
E
2 0 r
r2
dr
dr
U 1 2
(ln r2 ln r1 )
ln
2 0 r 2 0 r r
2 0
2 0 r1
r
r2
r2
1
1
C0
2 0 l
q
l
2 0
r
r
U
ln 1
ln 1
r2
r2
Заряд: q l , l – длина конденсатора; r1, r2 -радиусы электродов
C
2 0 l
r1
ln
r2

9.

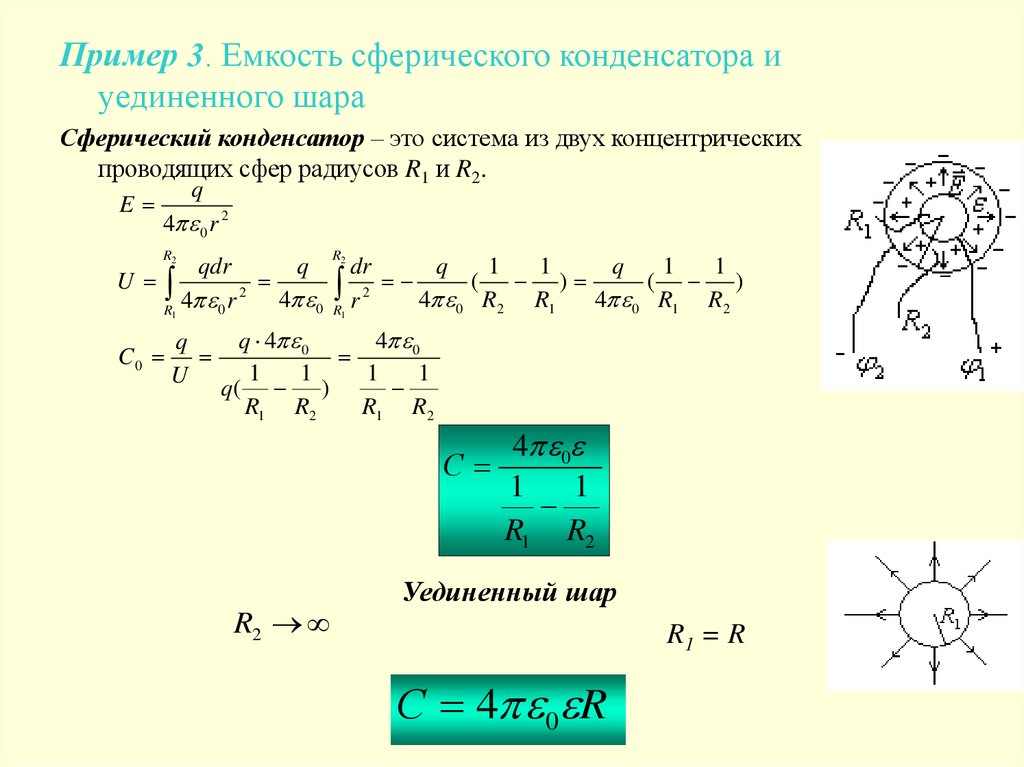
Пример 3. Емкость сферического конденсатора и
уединенного шара
Сферический конденсатор – это система из двух концентрических
проводящих сфер радиусов R1 и R2.
E
q
4 0 r 2
R2
qdr
q
U
2
4 0
R1 4 0 r
C0
q
U
R2
dr
q
1
1
q
1
1
(
)
(
R r 2 4 0 R2 R1 4 0 R1 R2 )
1
q 4 0
4 0
1
1
1
1
q( )
R1 R2
R1 R2
С
R2
4 0
1
1
R1 R2
Уединенный шар
R1 = R
С 4 0 R

10. 1.19. Соединение конденсаторов

Соединение конденсаторов бывает последовательным, параллельным и
смешанным.
1) Последовательное соединение.
При последовательном соединении заряды на всех
конденсаторах одинаковые, а напряжения разные
q1 q 2 ... q n q
U U 1 U 2 ... U n
q1 q 2
q
1
1
1
q
...
q(
...
)
C1 C 2
Cn
C1 C 2
Сn
C общ
1
1
1
1
...
Собщ С1 С2
Сn

11.

2) Параллельное соединение.
При параллельном соединении напряжения на всех конденсаторах
одинаковыеU1 U 2 ... U n = U, а заряды
– разные
q q1 q 2 ... q n C1U 1 C 2U 2 ...C nU n U (C1 C 2 ...C n ) C общ U
C общ C1 C 2 ... C n

12. 1.20. Энергия системы неподвижных точечных зарядов.

Как мы уже знаем, силы с которыми взаимодействуют заряженные тела,
являются потенциальными. Следовательно, система заряженных тел
обладает потенциальной энергией. Когда заряды удалены друг от
друга на бесконечность, они не взаимодействуют. Положим в этом
случае их энергию равной нулю.
Рассмотрим сначала систему, состоящую из двух точечных зарядов.
Сблизим заряды на заданное расстояние r. При этом мы совершим
работу против сил электрического поля, которая пойдет на увеличение
потенциальной энергии системы. Сближение зарядов можно
произвести, приближая q2 к q1 либо q1 к q2.

13.

В обоих случаях совершается одинаковая работа:
A W W , W 0,
W A q 2 ( 1 1 ), (1) 0,
W q 2 1 ;
W q 2 1
q
4 0 r
q 2 q1
q1
q2
1
1
q2
q1
или
4 0 r 2 4 0 r 2 4 0 r
1
(q1 2 q 2 1 )
2
Нетрудно убедиться в том, что потенциальная энергия системы трех неподвижных
точечных зарядов может быть представлена в виде:
W
W
1
(q1 1 2 3 q2 2 1 3 q3 3 1 2 )
2
В общем случае системы n неподвижных
точечных зарядов энергия системы
определяется по формуле:
1 n
W qi i
2 i 1

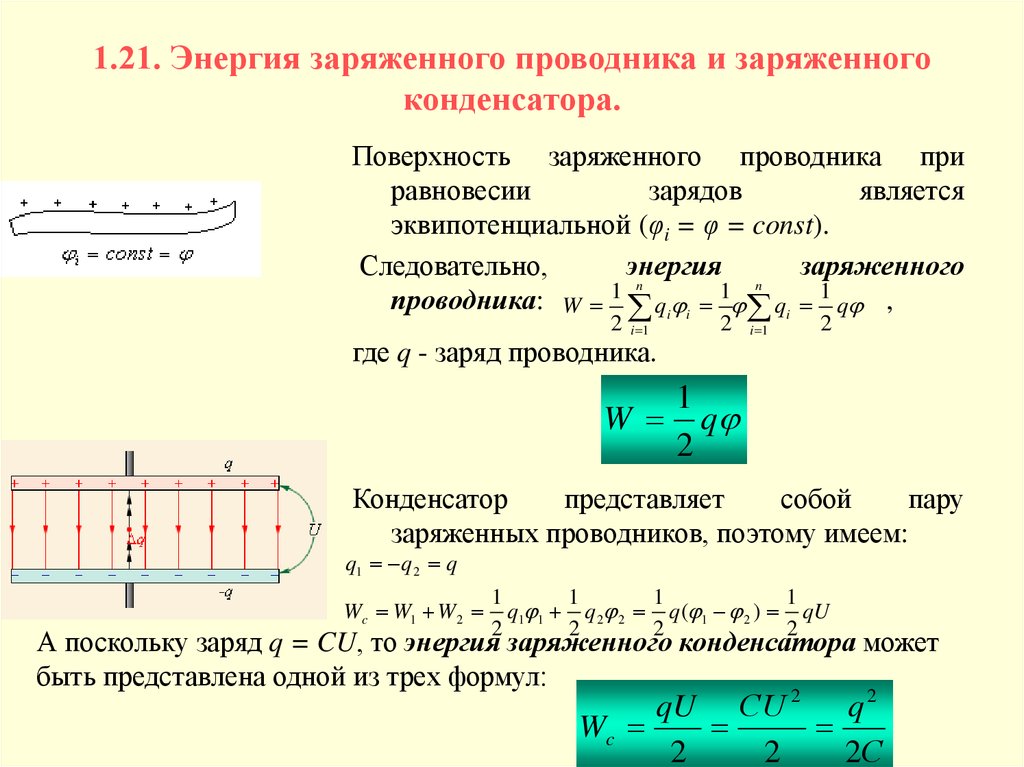
14. 1.21. Энергия заряженного проводника и заряженного конденсатора.

Поверхность заряженного проводника при
равновесии
зарядов
является
эквипотенциальной (φi = φ = const).
Следовательно,
энергия
заряженного
n
n
проводника: W 1 qi i 1 qi 1 q ,
2
i 1
2
где q - заряд проводника.
i 1
2
1
W q
2
Конденсатор
представляет
собой
пару
заряженных проводников, поэтому имеем:
q1 q 2 q
Wc W1 W2
1
1
1
1
q1 1 q 2 2 q ( 1 2 ) qU
2
2
2
2
А поскольку заряд q = CU, то энергия заряженного конденсатора может
быть представлена одной из трех формул:
qU СU 2 q 2
Wc
2
2
2С

15. 1.22. Энергия электростатического поля.

Выразим
энергию
заряженного
конденсатора
через
величины,
характеризующие электрическое поле, локализованное в пространстве
между его обкладками – напряженность поля Е и объем V, занятый полем.
Имеем для напряженности поля:
E
1 2
d 2 d1
U
где
d ,
U Ed
Воспользовавшись формулой для емкости плоского конденсатора C 0 S
d
находим:
CU 2 0 S E 2 d 2 0 E 2 ,
W
V
c
2
2d
2
где V = Sd - объём конденсатора, откуда следует, что
1
WE 0 E 2V
2
Мы видим, что энергия электрического поля прямо пропорциональна
квадрату его напряженности Е и объёму V, занятому полем. Величину
энергии поля, отнесенной к единице объема, называют плотностью
энергии:
wE
WE 1
Дж
0 E 2 3
V
2
м
- плотность энергии электрического поля.