Similar presentations:
Связь поляризованности диэлектрика в электростатическом поле с плотностью связанных зарядов
1. Занятие 2
∙ Связь поляризованности диэлектрика вэлектростатическом поле с плотностью связанных
зарядов
∙ Теорема Гаусса для поля D вектора
∙ Тангенциальные составляющие вектора
электрического смещения и напряжённости
электрического поля на границе раздела диэлектриков
∙ Нормальные составляющие вектора электрического
смещения, напряжённости и поляризованности на
границе раздела диэлектриков
∙ Ауд.: Иродов И.Е. Задачи по общей физике.
- М.: Бином, 1998 2010. №№ 2.32, 2.33, 2.93, 2.96
МГТУ им.
Н.Э. Баумана
2. Связь поляризованности диэлектрика в электростатическом поле с плотностью связанных зарядов
EΔScosα
σ′-
α
Δq′ΔV
n2
P
n1
l
σ′+
ΔS
Δq′+
d
Рис. 1
α
МГТУ им.
Н.Э. Баумана
В диэлектрике d толщиной, находящегося в
вакууме, выделен воображаемый косой цилиндр,
ось которого совпадает с направлением E вектора
напряжённости внешнего электрического поля, с l
длиной боковой поверхности, ΔS площадью
основания, в котором вектор P поляризованности
этого диэлектрика: P = ε0 χE, где χ диэлектрическая восприимчивость
вещества. Поверхностная плотность
связанных зарядов на σ ′+ правой и σ ′- левой
поверхностях диэлектрика: σ ′ = Pn,
3.
МГТУ им.Н.Э. Баумана
где Pn - проекция на внешнюю n нормаль к поверхности
диэлектрика P вектора поляризованности. Для правой
поверхности диэлектрика проекция Pn на внешнюю n2 нормаль к
поверхности диэлектрика вектора P поляризованности
положительна, вследствие этого σ ′+ > 0. Для левой поверхности
диэлектрика проекция Pn на внешнюю n1 нормаль к поверхности
диэлектрика вектора P поляризованности отрицательна,
вследствие этого σ ′- < 0. Связанный заряд на поверхности ΔS
площадью диэлектрика при условии его нахождения во внешнем
электрическом поле с E вектором напряжённости:
Δq′ = PΔScosα = PnΔS, (1)
где n - нормаль к поверхности диэлектрика; P - вектор
поляризованности диэлектрика и α - угол между n и P.
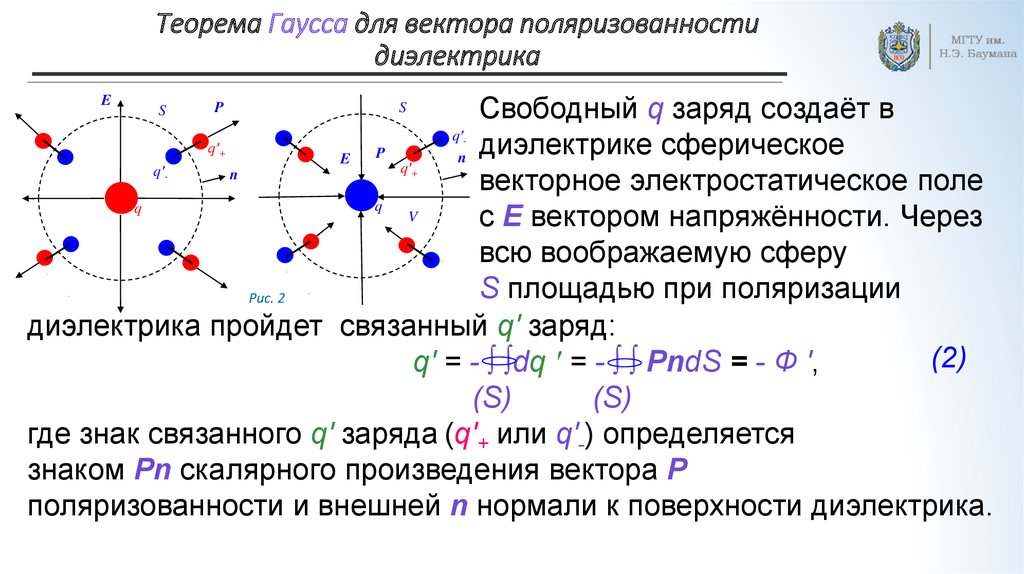
4. Теорема Гаусса для вектора поляризованности диэлектрика
МГТУ им.Н.Э. Баумана
Cвободный q заряд создаёт в
q′
q′
диэлектрике сферическое
P
n
E
q′
q′
n
векторное электростатическое поле
q
q
V
с E вектором напряжённости. Через
всю воображаемую сферу
S площадью при поляризации
Рис. 2
диэлектрика пройдет связанный q′ заряд:
(2)
q′ = - ∫ ∫dq ′ = - ∫ ∫ PndS = - Ф ′,
(S)
(S)
где знак связанного q′ заряда (q′+ или q′-) определяется
знаком Pn скалярного произведения вектора P
поляризованности и внешней n нормали к поверхности диэлектрика.
E
S
P
S
-
+
-
+
5.
МГТУ им.Н.Э. Баумана
Дивергенция (div) от P вектора поляризованности диэлектрика в
прямоугольной декартовой системе координат:
(3)
ρ′ = - ΔP = - divP = - [(∂PX/∂x) + (∂PY/∂y) + (∂PZ/∂z)],
где сумма приращений проекций PX; PY и PZ на оси OX, OY и OZ
координат вектора P поляризованности диэлектрика на единице
длины каждой из координат пропорциональна ρ′ объёмной
плотности связанного заряда, находящегося в рассматриваемой
точке объёма диэлектрика. Знак ρ′ объёмной плотности
связанного ρ′ заряда (ρ′+ или ρ′-) определяется знаком
[(∂PX/∂x) + (∂PY/∂y) + (∂PZ/∂z)].
6. Теорема Гаусса для поля D вектора
МГТУ им.Н.Э. Баумана
Вектор D электрического смещения или электрической индукции:
ε0E + P = D ↔ ε0E + ε0εE = D ↔ D = ε0(ε + 1)E,
(4)
где E, P векторы соответственно напряжённости электрического
поля и поляризованности диэлектрика.Теорема Гаусса для
электростатического поля в дифференциальной форме в
(5)
диэлектрике:
ΔD = ρ,
согласно которой ρ объёмная плотность свободных зарядов равна
дивергенции (div) вектора D электрического смещения в
рассматриваемой точке объёма диэлектрика. Теорема
Гаусса в интегральной форме в диэлектрике:
n
DdS dV фD dV dV qi . (6)
(S )
V
V
i 1
7.
МГТУ им.Н.Э. Баумана
Поток ФD вектора D электрического смещения через замкнутую
поверхность S площадью равен всему q свободному заряду,
распределённому с ρ объёмной плотностью в V объёме при
непрерывном распределении заряда или алгебраической сумме
заключённых внутри V объёма и ограниченных замкнутой
воображаемой поверхностью S площадью свободных qi
дискретных зарядов. Заряд в 1 Кл создаёт через замкнутую
воображаемую поверхность S площадью ND поток вектора D
электрического смещения, равного 1 Кл. Cиловые линии вектора D
электрического смещения начинаются и заканчиваются только на q
свободных зарядах.
8. Тангенциальные составляющие вектора электрического смещения и напряжённости электрического поля на границе раздела диэлектриков
aZ
O
X
ε2
τ
E2
dl
E2n
E1n
E2τ
L
σ-
E1
ε1
Y
dl
E1τ
b
Рис. 3
ε2 > ε1
МГТУ им.
Н.Э. Баумана
Cиловые линии вектора E
напряжённости электрического поля
находятся в OYZ плоскости.
Тангенциальная Eτ составляющая не
меняется на границе между
диэлектриками с ε1 и ε2 диэлектрическими проницаемостями при
отсутствии или наличии на границе между этими диэлектриками
свободного q заряда с поверхностной σ плотностью:
E1τ = E2τ. Тангенциальная Dτ составляющая вектора D
электрического смещения: D1τ/ε0ε1 =
= D2τ/ε0ε2 ↔ D1τ/D2τ = ε1/ε2 претерпевает разрыв.
9. Нормальные составляющие вектора электрического смещения,напряжённости и поляризованности на границе раздела диэлектриков
ВоображаемыйZ
Z
цилиндр с S
D
D
ε >ε D
ε >ε
S
S
D
S
площадью
S
n
n
P
оснований и b
ε
ε
b
D
P
b
σ
D
O
O
τ
P
σ′
ε D
Y
ε D
P σ′
D
Y
толщиной
D
X
X
τ
n
n
охватывает
D
Рис. 4
МГТУ им.
Н.Э. Баумана
2
2
1
2
2n
2
1
2n
2
2
2n
2
1
2τ
1n
+
1n
1
1τ
-
2
1
2τ
1n
1
1
2n
1n
+
1
D1τ
диэлектрики с ε1 и ε2 диэлектрическими проницаемостями при
наличии на границе между диэлектриками q свободного заряда с σ
поверхностной плотностью и при отсутствии его.
При переходе вектора E напряжённости
электрического поля через границу диэлектриков с
различными ε1, ε2 диэлектрическими
10.
МГТУ им.Н.Э. Баумана
проницаемостями при наличии на границе между этими
диэлектриками q свободного заряда с σ поверхностной плотностью
модули D1n, D2n векторов D1n, D2n нормальных составляющих
векторов электрического смещения, а также модули E1n, E2n
векторов E1n, E2n нормальных составляющих напряжённости
электрического поля претерпевают разрыв:
(7)
D2n - D1n= σ; E2n = (ε1E1n/ε2) + (σ/ε0ε2).
При переходе вектора E напряжённости электрического поля через
границу диэлектриков с различными ε1, ε2 диэлектрическими
проницаемостями при отсутствии на границе между этими
диэлектриками свободного заряда модули D1n, D2n
векторов D1n, D2n нормальных составляющих векторов
электрического смещения остаются постоянными:
D1n= D2n, а модули E1n, E2n
11.
МГТУ им.Н.Э. Баумана
векторов E1n, E2n нормальных составляющих напряжённости
электрического поля претерпевают разрыв: E1n/E2n = ε2/ε1.
Разность проекций P2n, P1n на внешние n2 и n1 нормали вектора
P поляризованности в диэлектриках с соответственно ε2 и ε1
диэлектрическими проницаемостями равна со знаком "-" σ′
поверхностной плотности связанных зарядов на границе этих
диэлектриков: P2n - P1n = - σ′. Знак σ′ поверхностной плотности
связанных зарядов на границе диэлектриков(σ ′+ или σ ′-)
определяется соотношением модулей P2n, P1n векторов
P2n, P1n нормальных составляющих поляризованности
в диэлектриках с ε2, ε1 диэлектрическими
проницаемостями.
12. Задача №2.32
МГТУ им.Н.Э. Баумана
Система состоит из шара R радиуса, заряженного сферически –
симметрично, и окружающей среды, заполненной зарядом с
ρ = α/r объёмной плотностью, где α – постоянная, r – расстояние
от центра шара. Пренебрегая влиянием вещества, найти заряд
шара, при котором модуль напряженности электрического поля
вне шара не зависит от r. Чему равна эта напряжённость?
Ответ: q = 2πR2 α, E = α/2ε0.
13. Решение
МГТУ им.Н.Э. Баумана
Решение
Дано: ρ = α/r, R/q = ? E = ?
Согласно теореме Гаусса модуль E вектора E напряжённости
электростатического поля в M точке на сфере
R
Z
E
E
ε0
n
+
+
M
q
ρ=α/r
O
+
+
E
Y
S, V
E
X
r
Рис.5
14.
МГТУ им.Н.Э. Баумана
r радиусом, охватывающей q заряд и шаровой слой,
заряженный с объёмной плотностью ρ = α/r, с внутренним
R радиусом, внешним r радиусом:
1
EdS
(S )
2
dV
E
4
r
0 V
1
r
(q 4 r 2 dr )
0
r
R
2
1
q
2
R
2
2
2
E 4 r [q 2 (r R )] E
E
, (8)
2
0
2 0
2 0
4 r 0
Если q = 2παR2.
15. Задача №2.33
МГТУ им.Н.Э. Баумана
Внутри шара, заряженного равномерно с ρ объёмной плотностью,
имеется сферическая полость. Центр полости смещен
относительно центра шара на a вектор расстояния. Пренебрегая
влиянием вещества шара, найти E вектор напряжённости
электростатического поля внутри полости.
Ответ: E = aρ/3ε0.
16. Решение
aZ
E1
M
r1
O
r2
E = E1 + E2
a
Y
E2
Рис.6
МГТУ им.
Н.Э. Баумана
Дано: ρ, a/E = ?
Электростатическое поле,
вследствие его центральной
симметрии, достаточно определить
в его сечении, например,в OYZ
плоскости. Представляем шар со
сферической полостью двумя
шарами с положительным и
отрицательным зарядами с
ρ и -ρ объёмными плотностями, вложенными друг в
друга со смещением их центров на длину a вектора.
Тогда в пересечении этих шаров заряд отсутствует.
17.
Согласно теореме Гаусса модули E1, E2 векторов E1, E2 насферической поверхности r1, r2 радиусами в M точке каждого
заряженного шара, т.е. внутри полости:
3
1
E
d
S
1, 2
(S )
0
dV
V
E1, 2 4 r1, 2
2
4 r1, 2
3 0
E1, 2
r1, 2
3 0
,
МГТУ им.
Н.Э. Баумана
(9)
Вследствие отрицательного заряда, охватываемого сферической
поверхностью r2 радиусом, E2 вектор направлен противоположно r2
r
r
радиусу-вектору:
1
2
(10)
E
;E .
1
3 0
2
3 0
Вектор E = E1 + E2 напряжённости электростатического поля в M
точке, т.е. внутри полости, как суперпозиция векторов
E1, E2 от каждого заряженного шара r1 ,r2 радиусами:
a
E E1 E 2
(r1 r2 )
, (11)
3 0
3 0
где r1 – r2 = a. Вектор E сонаправлен a вектору и OY оси.
18. Задача №2.93
Сторонние заряды равномерно распределены сρ объёмной плотностью по шару R радиуса из однородного
изотропного диэлектрика с ε проницаемостью. Найти:
а) модуль напряжённости электрического поля как функцию r
расстояния центра шара; изобразить примерные графики E(r) и
φ(r) зависимостей; б) объёмную и поверхностную плотности
связанных зарядов.
Ответ: а) Модуль E(r < R) = ρr/3εε0, E(r > R) = ρR3/3ε0r2;
б) ρ′ = -ρ(ε – 1)/ε, σ ′ = ρR(ε – 1)/3ε.
φ
E
R
r
R
r
МГТУ им.
Н.Э. Баумана
19. Решение
RZ
S2
n1
M1
ε
r1
S,V
+
+
D1
E1
O
+
S1,V1
ρ
+
r2
X
M2
Рис.7
Дано: R, ε, ρ / E(r) = ? φ(r) = ? ρ′ = ? σ′ = ?
Поток ФD1 вектора D1 электрического
P
смещения согласно теореме Гаусса для
поля D вектора через воображаемую
сферическую поверхность S1 площадью и
Y
r1 радиусом, которая охватывает V1 объём с
3/3 зарядом:
4ρπr
1
E
3
4 r13
4 r1
r1 (12)
2
ФD1 D1dS
D1r 4 r1
D1r
,
D
2
M
n
МГТУ им.
Н.Э. Баумана
2
n2
( S1 )
3
3
где D1r проекция вектора D1 электрического смещения на
направление r1 радиуса – вектора в произвольной M1
точке пространства диэлектрика внутри шара, т.е.
при r1 ≤ R.
3
20.
МГТУ им.Н.Э. Баумана
В однородном изотропном диэлектрике D = εε0 E, поэтому проекция
E1r вектора E1 напряжённости электростатического поля на
направление r1 радиуса – вектора в произвольной M1 точке
пространства диэлектрической среды внутри шара, т.е. при r1 ≤ R:
E1r
D1r
0
r1
. (13)
3 0
Поток ФD2 вектора D2 электрического смещения согласно теореме
Гаусса для поля D вектора через воображаемую сферическую
поверхность S2 площадью и r2 радиусом, которая охватывает V2
объём с 4ρπR3/3 зарядом:
ФD 2
4 R 3
4 R 3
R 3
2
D2 dS
D2r 4 r2
D2r 2 ,
3
3
3r2
( S2 )
(14)
где D2r проекция вектора D2 электрического смещения
21.
на направление r2 радиуса – вектора в произвольной M2точке в вакууме вне шара, т.е. при r2 ≥ R. В вакууме D = ε0E, поэтому
проекция E2r вектора E2 напряжённости электростатического поля на
направление r2 радиуса – вектора в произвольной M2 точке в
3
D
R
вакууме вне шара, т.е. при r2 ≥ R:
E 2 r 2 r 2 . (15)
МГТУ им.
Н.Э. Баумана
0
3r2 0
В M точке на границе раздела заряженный диэлектрический шар –
вакуум отношение проекции E1r вектора E1 напряжённости
электростатического поля внутри шара, т.е. при r1 ≤ R, к проекции
E2r вектора E2 напряжённости электростатического
поля вне шара, т.е. при r2 ≥ R, поскольку E1r, E2r
являются проекциями нормальных составляющих
вектора напряжённости:
22.
E1rE
1
2 1r ,
E2 r
1
E2 r
(16)
где ε1 = 1 – диэлектрическая проницаемость вакуума;
ε2 = ε – диэлектрическая проницаемость заряженного
шара.
E
Примерный график E(r) зависимости:
На границе раздела заряженный
диэлектрический шар – вакуум проекция E1r
вектора E1 напряжённости электростатического
0
R
поля внутри шара, т.е. при r1 ≤ R, и проекция E2r
Рис.8
вектора E2 напряжённости электростатического
МГТУ им.
Н.Э. Баумана
r
поля вне шара, т.е. при r2 ≥R, претерпевают разрыв.
Потенциал φ1 внутри заряженного шара, т.е. при
r1 ≤ R, считая потенциал на
r
23.
МГТУ им.Н.Э. Баумана
бесконечном расстоянии от этого шара, равным нулю, согласно
cвязи напряжённости и разности потенциалов в
электростатическом поле в интегральной форме:
R
R
( R 2 r1 2 ) R 2
r
R 3
(17)
1 E1r dr E2 r dr
dr 2 dr
.
r1
R
r1
3 0
R
6 0
3r 0
3 0
Потенциал φ2 вне заряженного шара, т.е. при r2 ≥ R, считая
потенциал на бесконечном расстоянии от этого шара, равным
нулю, согласно cвязи напряжённости и разности потенциалов в
электростатическом поле в интегральной форме:
φ
2
2
R 3
R 3
2 E 2r dr 2 dr
. (18)
3 0 r
r
r 3r 0
Примерный график φ(r):
0
R
Рис.9
r
24.
Потенциал φ1 внутри заряженного шара монотонноуменьшается от максимального значения в его 0 центре до
значения на поверхности и уменьшается до нуля
R 2
1 r R
при r→∞:
3 0
1
МГТУ им.
Н.Э. Баумана
(19)
Вектор P = ε0(ε – 1)E поляризации в однородном изотропном
диэлектрике коллинеарен и совпадает в нём по направлению с
вектором E напряжённости электростатического поля. Вектор E
направлен по вектору n нормали к сферической поверхности
заряженного диэлектрического шара S площадью. Поэтому вектор
P поляризации тоже направлен по этому вектору n нормали,
вследствие чего он имеет только нормальную Pn
проекцию к сферической поверхности заряженного
диэлектрического шара S площадью. Поверхностная
σ′ плотность связанных зарядов:
25.
МГТУ им.Н.Э. Баумана
r1
R
Pn P cos( P n) 0 ( 1) E1r cos( P n) 0 ( 1) E1r 0 ( 1)
( 1)
, (20)
3 0
3
где P = ε0(ε – 1)E1r – модуль вектора P поляризации, поскольку
вектор E напряжённости имеет одну E1r проекцию; r1 = R, т.к.имеет
место поверхность шара. Полный qσ ′ связанный заряд на
сферической поверхности заряженного диэлектрического шара S =
3
2
R
(
1
)
4
(
1
)
R
4πR площадью:
(21)
q S
4 R 2
.
3
3
Объёмная ρ′ плотность связанных зарядов с учётом того, что
векторы P поляризации внутри заряженного
диэлектрического шара образуют сферическое
векторное поле с P1r проекцией на направление
r1 радиуса – вектора:
26.
r 2 0 ( 1) r2
2
3
1 ( r P1r )
1 [ r 0 ( 1) E1r ]
1
0
( 1) .
divP 2
2
2
r
r
r
r
r
r
Полный qρ′ объёмный заряд в V = 4πR3/3 объёме заряженного
3
4
(
1
)
R
диэлектрического шара:
q V
.
3
МГТУ им.
Н.Э. Баумана
(22)
(23)
Согласно закону сохранения электрических зарядов
электронейтральность диэлектрика должна сохранится после
введения в него сторонних зарядов, что выполняется при равенстве
модулей и противоположности знаков полного qσ′ связанного заряда
на сферической поверхности заряженного диэлектрического шара и
полного qρ′ объёмного заряда в его объёме :
4( 1) R 3 4( 1) R 3
q q
0,
3
3
что является проверкой правильности решения.
(24)
27. Задача №2.96
МГТУ им.Н.Э. Баумана
Первоначально пространство между обкладками плоского
конденсатора заполнено воздухом и напряжённость
1
электрического поля в зазоре равна E0.
ε
Затем половину зазора, как показано на рис., 2
заполнили однородным диэлектриком с проницаемостью ε.
Найти модули векторов E и D в обеих частях зазора (1 и 2), если
при введении диэлектрика: а) напряжение между обкладками не
менялось; б) заряды на обкладках оставались неизменными.
Ответ: а) E1 = 2εE0 /(ε + 1), E2 = 2E0 /(ε + 1),
D1 = D2 = 2εε0E0 /(ε + 1); б) E1 = E0, E2 = E0/ε,
D1 = D2 = ε0E0.
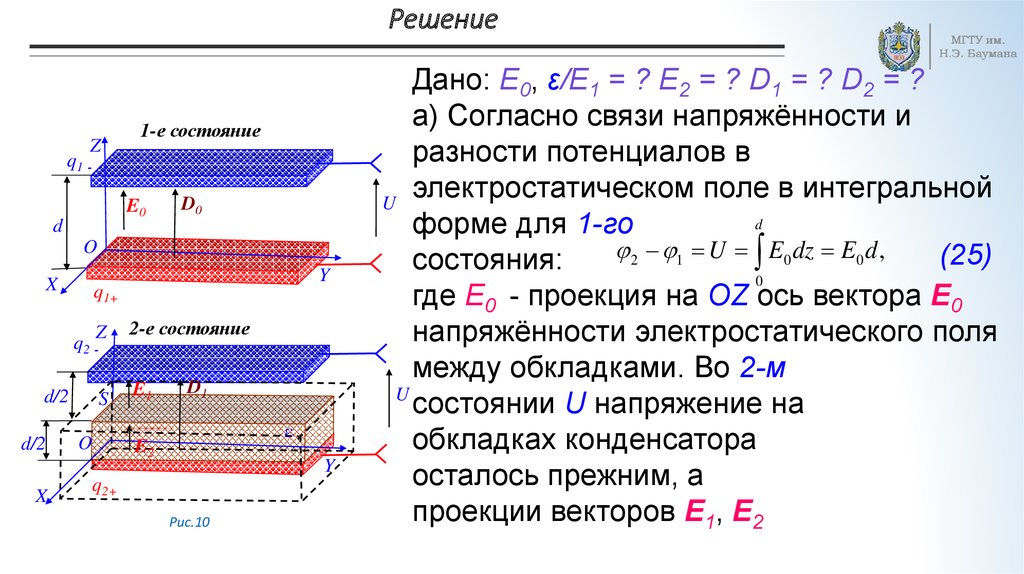
28. Решение
Z1-е состояние
q1 -
E0
d
D0
O
X
Z
q2 d/2
d/2
X
Y
q1+
S
O
2-е состояние
E1
D1
ε
E2
Y
q2+
Рис.10
МГТУ им.
Н.Э. Баумана
Дано: E0, ε/E1 = ? E2 = ? D1 = ? D2 = ?
а) Cогласно cвязи напряжённости и
разности потенциалов в
электростатическом поле в интегральной
U
d
форме для 1-го
2 1 U E0 dz E0 d ,
(25)
состояния:
0
где E0 - проекция на OZ ось вектора E0
напряжённости электростатического поля
между обкладками. Во 2-м
U
состоянии U напряжение на
обкладках конденсатора
осталось прежним, а
проекции векторов E1, E2
29.
на OZ ось напряжённости электростатического поля междуобкладками соответственно в вакууме, диэлектрике стали равными
d
d
E1, E2 :
U E1 E2 .
(26)
МГТУ им.
Н.Э. Баумана
2
2
Поток ФD1 вектора D1 электрического смещения во 2-м состоянии
согласно теореме Гаусса для поля D вектора через воображаемый
параллелепипед с учётом пересечения вектором D1 только его
верхнего основания S площадью одинаков в вакууме
диэлектрике:
и
ФD D1 dS q 2 ,
(27)
1
(S )
где q2+ - охватываемый воображаемым параллелепипедом заряд
на нижней обкладке конденсатора, одинаковый для
вакуума и диэлектрика. В однородном изотропном
диэлектрике D = εε0E, поэтому E1, E2 проекции на
OZ ось векторов E1, E2 напряжённости
30.
МГТУ им.Н.Э. Баумана
электростатического поля между обкладками соответственно в
D1 0 E1 ; D1 0 E2 E1 E2 . (28)
вакууме, диэлектрике:
Приравниваем выражения U напряжения на обкладках
конденсатора для 1-,2-го состояний:
2 E0
2 E0
2 0 E0
E1d E2 d
E2 d E2 d
E0 d
E0 d
E2
E1
D1
.
2
2
2
2
1
1
1
Z
q1 -
S
1-е состояние
E0
D0
O
Y
X
q1+
(29)
б) Для 1-го состояния поток ФD0
U вектора D0 электрического смещения
согласно теореме Гаусса для поля D
вектора через воображаемый
параллелепипед
Рис.11
с учётом пересечения в вакууме вектором D0
31.
только его верхнегооснования S площадью:
ФD0 D0 dS q1 , ФD0 D0 S q1 q1 D0 S q1 0 E0 S
МГТУ им.
Н.Э. Баумана
(30)
S
где q1+ - охватываемый воображаемым параллелепипедом заряд
на нижней обкладке конденсатора.
Поток ФD0 вектора D0 электрического
2-е состояние
Z
q1смещения во 2-м состоянии согласно
D0
d/2
теореме Гаусса для поля D вектора через
S E1
ε
воображаемый параллелепипед с учётом
O
d/2
E2
Y
пересечения вектором D0 только его
X
q1+
Рис.12
верхнего основания S площадью одинаков в
вакууме и диэлектрике:
32.
q10 E0 S
N D0 D0 dS q1 , N D0 D0 S q1 D0
D0
D0 0 E0 , (31)
S
S
S
МГТУ им.
Н.Э. Баумана
где q1+ - охватываемый воображаемым параллелепипедом заряд
на нижней обкладке конденсатора, величина которого равна q1+
заряду в 1-ом состояния, вследствие отключения источника
напряжения.
В однородном изотропном диэлектрике D = εε0E, поэтому E1, E2
проекции векторов E1, E2 на OZ ось напряжённости
электростатического поля между обкладками соответственно в
вакууме, диэлектрике: E1 D0 E0 0 E0 ; E2 D0 E0 0 E0 . (32)
0
0
0
Дома: Иродов И.Е. Задачи по общей физике.
- М.: Бином, 1998 2010. №№ 2.37, 2.99
Спасибо за внимание!
0






























 physics
physics








