Презентация к уроку геометрии в 7 классе "Равнобедренные и равносторонние треугольники. Признаки и свойства равнобедренного треугол

1.

Равнобедренный треугольник
Если у треугольника две стороны
равны,
то
такой
треугольник
называют равнобедренным.
Равные стороны называют боковыми, а
третью сторону — основанием.
AB=BC — боковые стороны ,
AC — основание.
Если у треугольника все три стороны
равны,
то
такой
треугольник
является равносторонним.

2.

Равнобедренный треугольник имеет некоторые свойства:
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведённая к
основанию, является медианой и высотой.
3. В равнобедренном треугольнике медиана, проведённая к
основанию, является биссектрисой и высотой.
4. В равнобедренном треугольнике высота, проведённая к
основанию, является биссектрисой и медианой.

3.

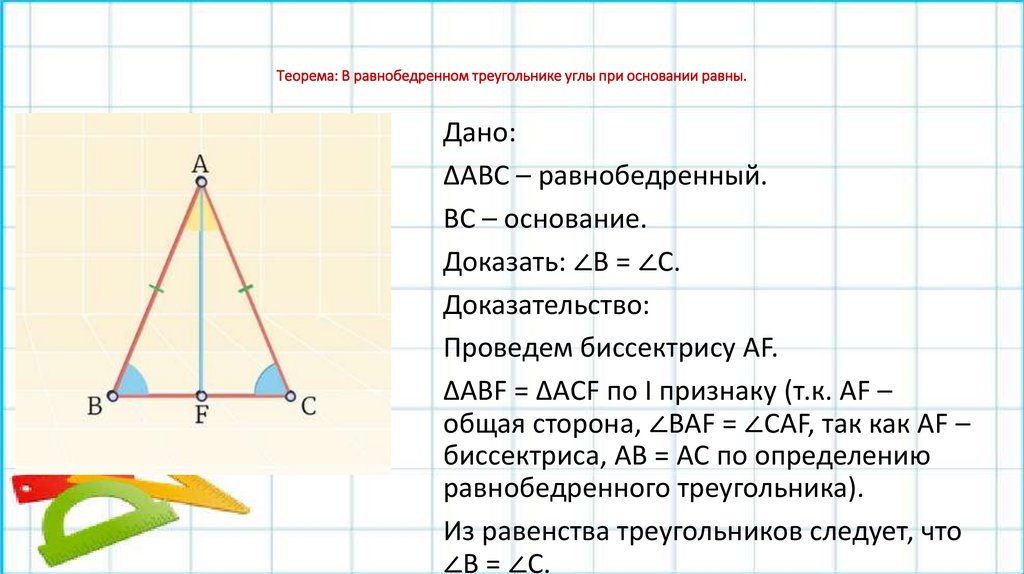
Теорема: В равнобедренном треугольнике углы при основании равны.
Дано:
ΔABC – равнобедренный.
BC – основание.
Доказать: ∠B = ∠C.
Доказательство:
Проведем биссектрису АF.
∆ABF = ∆ACF по I признаку (т.к. AF –
общая сторона, ∠BAF = ∠CAF, так как AF –
биссектриса, AB = AC по определению
равнобедренного треугольника).
Из равенства треугольников следует, что
∠B = ∠C.

4.

В равнобедренном треугольнике биссектриса, проведённая к основанию, является
медианой и высотой треугольника.
Дано: ΔABC – равнобедренный, BC– основание ΔABC
AF– биссектриса ΔABC
Доказать: AF – медиана и высота.
Доказательство:
∆ABF = ∆ACF по I признаку (т.к. AF – общая сторона, ∠BAF = ∠CAF, так как
AF –биссектриса, AB = AC по определению равнобедренного
треугольника).
Из равенства треугольников следует, что BF = FC, значит, F – середина
BC, AF – медиана.
∠AFB =∠AFC (как соответствующие элементы равных треугольников), их
сумма равна 180 градусам (по свойству развернутого угла).
∠AFB = ∠AFC = 90°
Значит, AF – высота треугольника (по определению высоты).

5.

.
Медиана равнобедренного треугольника, проведённая к основанию, является высотой и
биссектрисой.
Дано: ΔABC – равнобедренный, BC– основание ΔABC
AF – медиана ΔABC
Доказать: AF – биссектриса и высота ΔABC.
Доказательство:
∆ABF = ∆ACF по I признаку (∠В = ∠С по свойству равнобедренного треугольника, BF = CF по определению медианы треугольника, AB = AC по
определению равнобедренного треугольника).
Из равенства треугольников следует, что ∠BАF = ∠FАC. Значит, AF - биссектриса ΔABC (по определению биссектрисы треугольника).
∠AFB = ∠AFC как соответствующие элементы равных треугольников, но их сумма равна 180 (по свойству развернутого угла).
∠AFB = ∠AFC = 90°. Значит, AF – высота треугольника (по определению высоты треугольника).

6.

Задача 1
Периметр равнобедренного треугольника ABC
равен 50 см, боковая сторона AВ на 4 см больше
основания АC. Найдите основание треугольника.
Решение: Пусть х – основание АС треугольника АВС,
тогда АВ = СВ (как боковые стороны
равнобедренного треугольника).
АВ = ВС = х + 4 (по условию).
Периметр треугольника АВС равен сумме всех его
сторон, т. е. 50 см = АС + ВС + АВ,
50 = (х + 4) + (х + 4) + х,
50 = 3х + 8,
3х = 50 – 8,
3х = 42,
х = 14 см – основание АC.

7.

Задача 2
На рисунке изображён равнобедренный
треугольник ABC. AC – основание треугольника,
∠1 = 120. Найдите ∠2.
Решение:
∠1 и ∠АСВ – смежные →∠1 + ∠АСВ = 180,
значит:
∠АСВ = 180 – 120 = 60
АВС – равнобедренный, значит: ∠ВАС = ∠АСВ
= 60 (углы при основании равнобедренного
треугольника равны).
∠2 = ∠ВАС = 60 (как вертикальные углы).
Ответ: ∠ 2 = 60.

8.

Задача 3
Дано: ABC, высота BH, BA = 5 см.
CAB = 50°, HBC = 40°.
Найти: BC
Решение:
Сумма углов треугольника равна 180°, а значит
в Δ ABH мы можем узнать ABH, который
будет равен 180° − 50° − 90° = 40°.
Получается, что ABH и HBC равны по 40° и
BH — биссектриса.
Так как BH является и биссектрисой, и высотой,
то Δ ABC — равнобедренный, а значит BC = BA =
5 см.
Ответ: 5 см.