Треугольники. Решение задач

1.

“Треугольники”

2.

§1. Треугольники
а) Треугольники
б) Равные треугольники
в) Первый признак равенства треугольников
§2. Медианы, биссектрисы и высоты треугольников
а) Перпендикуляр к прямой
б) Медианы, биссектрисы и высоты треугольников
в) Свойства равнобедренного треугольника
§3. Второй и третий признак равенства треугольников
а) Второй признак равенства треугольников
б) Третий признак равенства треугольников
§4. Окружность
а) Окружность

3.

ACB
С
BAC
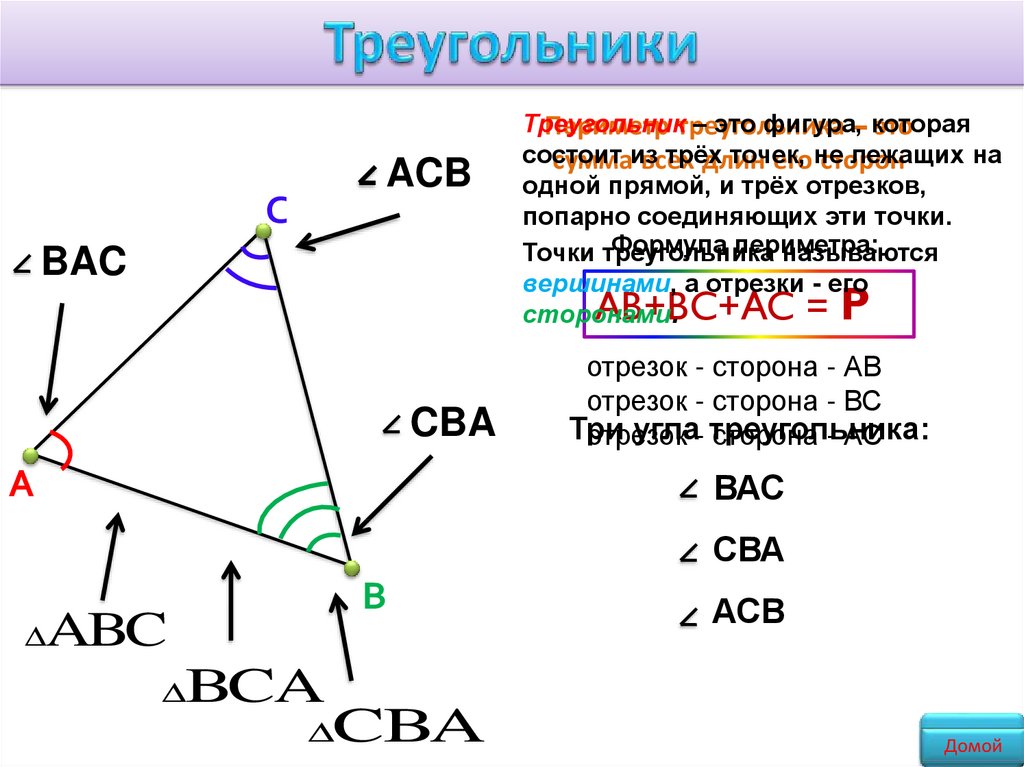
Треугольник
– это фигура,– которая
Периметр треугольника
это
состоит
трёх
точек,
лежащих на
суммаиз
всех
длин
его не
сторон
одной прямой, и трёх отрезков,
попарно соединяющих эти точки.
Формула периметра:
Точки треугольника
называются
вершинами, а отрезки - его
AB+BC+AC =
сторонами.
P
CBA
А
отрезок - сторона - АВ
отрезок - сторона - ВС
Три
угла- треугольника:
отрезок
сторона - АС
ВАС
СВА
В
ABC
BCA
АСВ
CBA
Домой

4.

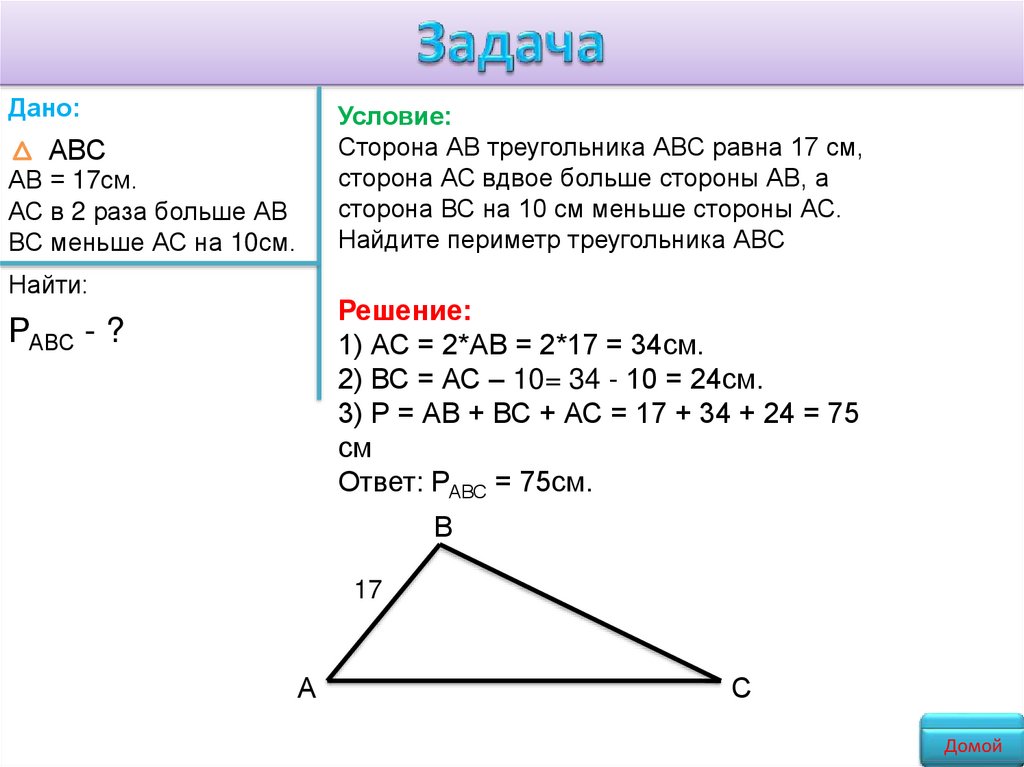
Дано:
Условие:
Сторона АВ треугольника АВС равна 17 см,
сторона АС вдвое больше стороны АВ, а
сторона ВС на 10 см меньше стороны АС.
Найдите периметр треугольника АВС
АВС
АВ = 17см.
АС в 2 раза больше АВ
ВС меньше АС на 10см.
Найти:
Решение:
1) АС = 2*АВ = 2*17 = 34см.
2) ВС = АС – 10= 34 - 10 = 24см.
3) Р = АВ + ВС + АС = 17 + 34 + 24 = 75
см
Ответ: РАВС = 75см.
РАВС - ?
В
17
А
С
Домой

5.

Домой

6.

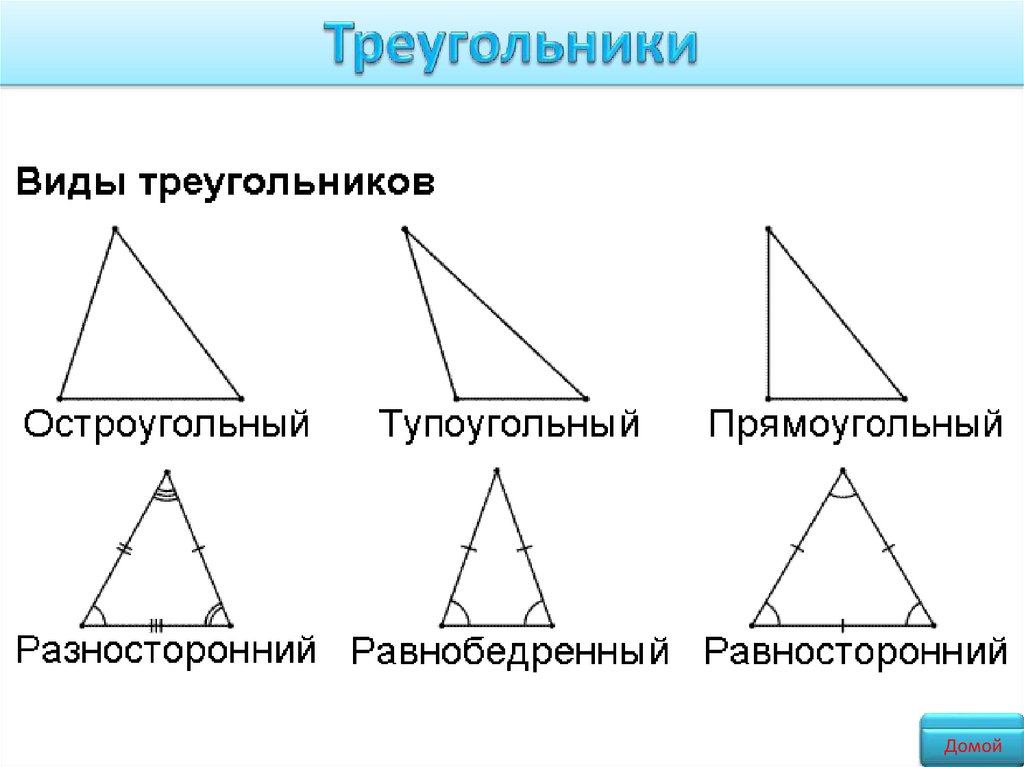
Остроугольный треугольник – это такой
треугольник, у которого все углы острые
( <90o ).
Равносторонний треугольник – это
такой треугольник, у которого все
стороны равны по величине между
собой.
Тупоугольный треугольный – это
такой треугольник, у которого хотя бы
один угол тупой ( >90o ).
Равнобедренный треугольник – это
такой треугольник, у которого
боковые стороны равны по величине.
Прямоугольный треугольник – это
такой треугольник, у которого есть прямой
угол ( 90о ).
Разносторонний треугольник – это
такой треугольник, у которого все
стороны разные по величине.
Домой

7.

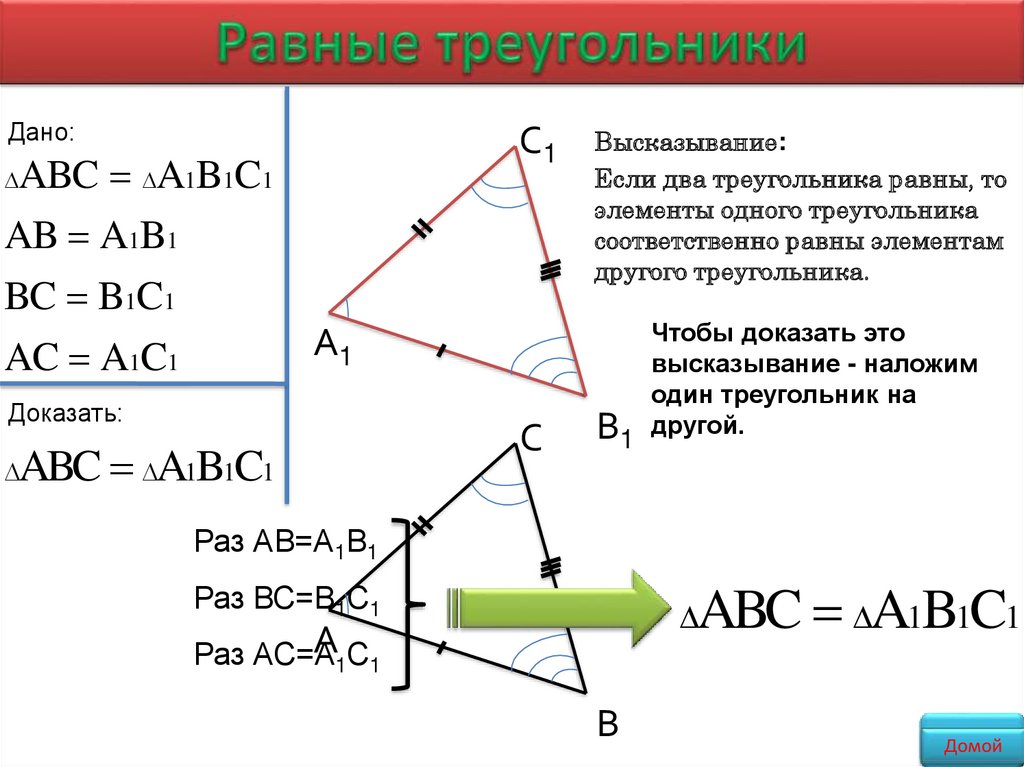
Дано:
С1
ABC A1B1C1
AB A1B1
BC B1C1
AC A1C1
Высказывание:
Если два треугольника равны, то
элементы одного треугольника
соответственно равны элементам
другого треугольника.
А1
Доказать:
ABC A1B1C1
С
В1
Чтобы доказать это
высказывание - наложим
один треугольник на
другой.
Раз АВ=А1В1
ABC A1B1C1
Раз ВС=В1С1
А1С1
Раз АС=А
В
Домой

8.

Дано:
Условие:
Отрезки АЕ и DC пересекаются в
точке В, являющейся серединой
каждого из них. Докажем, что
треугольники АВС и EBD равны.
ÀÅ DC
АВ = ВЕ
DB = BC
Доказать:
АВС =
ЕВD
Доказательство:
1) Рассмотрим АВС и
ЕВD
AB = EB (по усл.)
СВ = DB (по усл.)
АВС = DBE ( вертик.),
АВС = EBD ( по 2 стор. и углу между ними)
А
С
В
D
E
Домой

9.

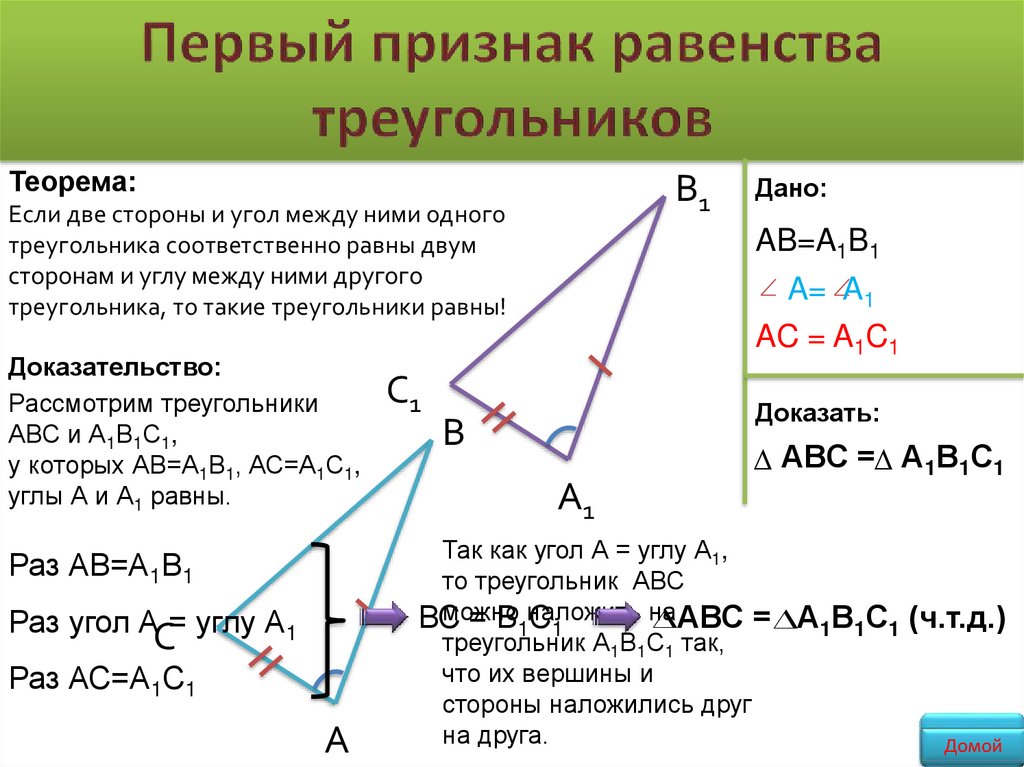
Теорема:
В1
Если две стороны и угол между ними одного
треугольника соответственно равны двум
сторонам и углу между ними другого
треугольника, то такие треугольники равны!
Доказательство:
Рассмотрим треугольники
АВС и А1В1С1,
у которых АВ=А1В1, АС=А1С1,
углы А и А1 равны.
Раз АВ=А1В1
Раз угол А = углу А1
С
Раз АС=А1С1
А
Дано:
AB=A1B1
A= A1
AC = A1C1
С1
Доказать:
В
А1
АВС = А1В1С1
Так как угол А = углу А1,
то треугольник АВС
можно
на
АВС = А1В1С1
ВС
= В1наложить
С1
треугольник А1В1С1 так,
что их вершины и
стороны наложились друг
на друга.
(ч.т.д.)
Домой

10.

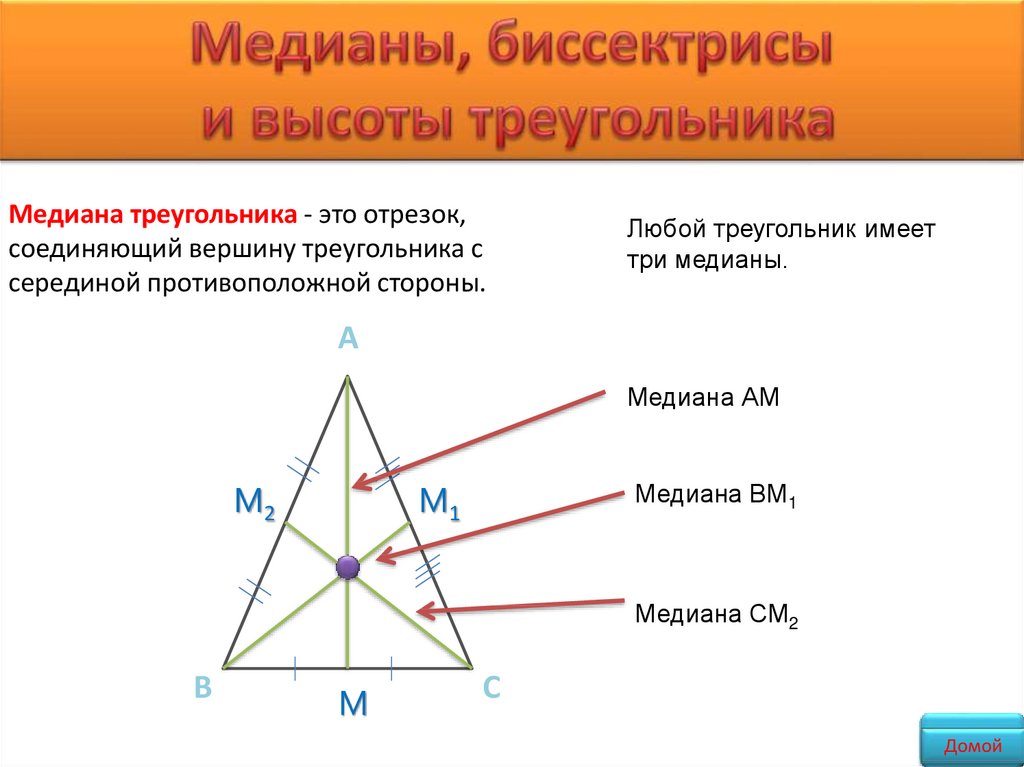
Медиана треугольника - это отрезок,
соединяющий вершину треугольника с
серединой противоположной стороны.
Любой треугольник имеет
три медианы.
А
Медиана АМ
M2
M1
Медиана ВМ1
Медиана СМ2
В
M
С
Домой

11.

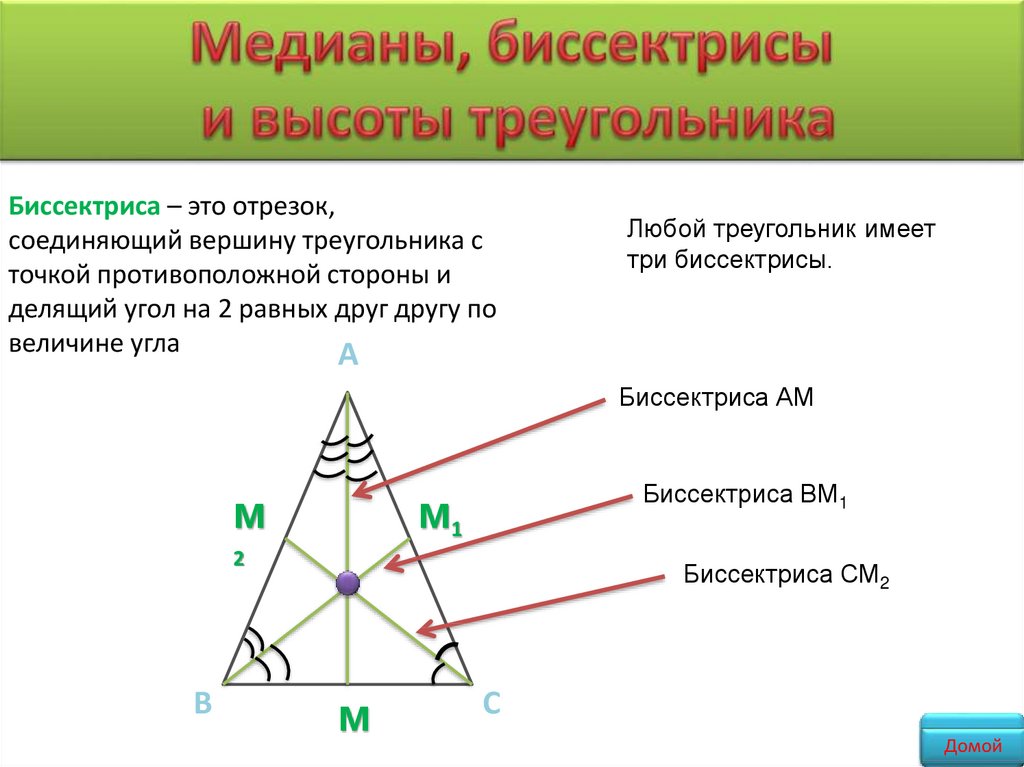
Биссектриса – это отрезок,
соединяющий вершину треугольника с
точкой противоположной стороны и
делящий угол на 2 равных друг другу по
величине угла
А
Любой треугольник имеет
три биссектрисы.
Биссектриса АМ
M
Биссектриса ВМ1
M1
2
В
Биссектриса СМ2
M
С
Домой

12.

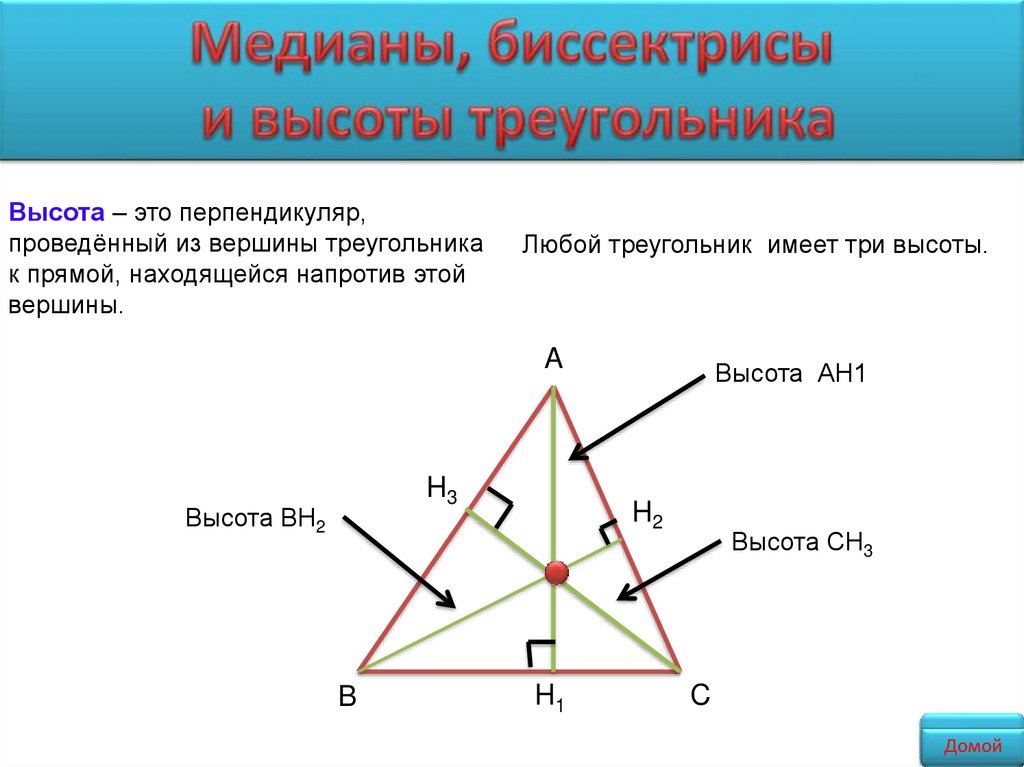
Высота – это перпендикуляр,
проведённый из вершины треугольника
к прямой, находящейся напротив этой
вершины.
Любой треугольник имеет три высоты.
A
H3
Высота ВН2
B
Высота АН1
H2
H1
Высота СН3
C
Домой

13.

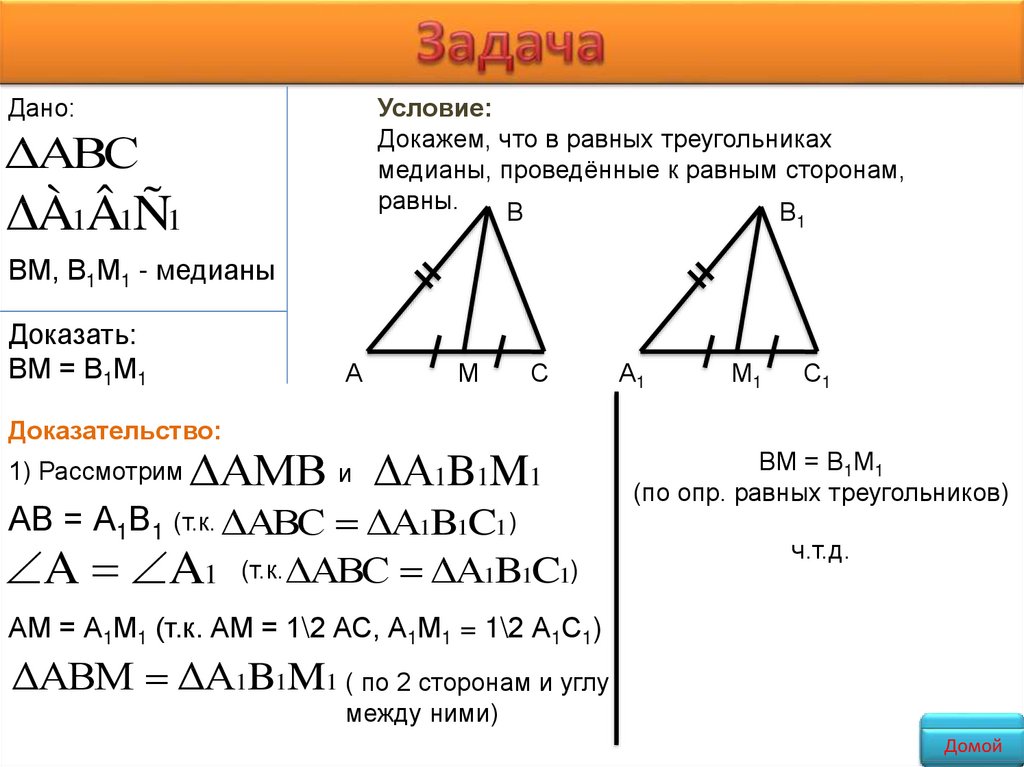
Дано:
Условие:
Докажем, что в равных треугольниках
медианы, проведённые к равным сторонам,
равны.
В
В
ΔABC
ΔÀ1Â1Ñ1
1
ВМ, В1М1 - медианы
Доказать:
ВМ = В1М1
А
М
С
А1
М1
С1
Доказательство:
1) Рассмотрим
ΔAMB и ΔA1B1M1
АВ = А1В1 (т.к. ΔABC ΔA1B1C1 )
A A
1 (т.к.ΔABC
ΔA1B1C1)
ВМ = В1М1
(по опр. равных треугольников)
ч.т.д.
АМ = А1М1 (т.к. АМ = 1\2 АС, А1М1 = 1\2 А1С1)
ΔABM ΔA1B1M1 ( по 2 сторонам и углу
между ними)
Домой

14.

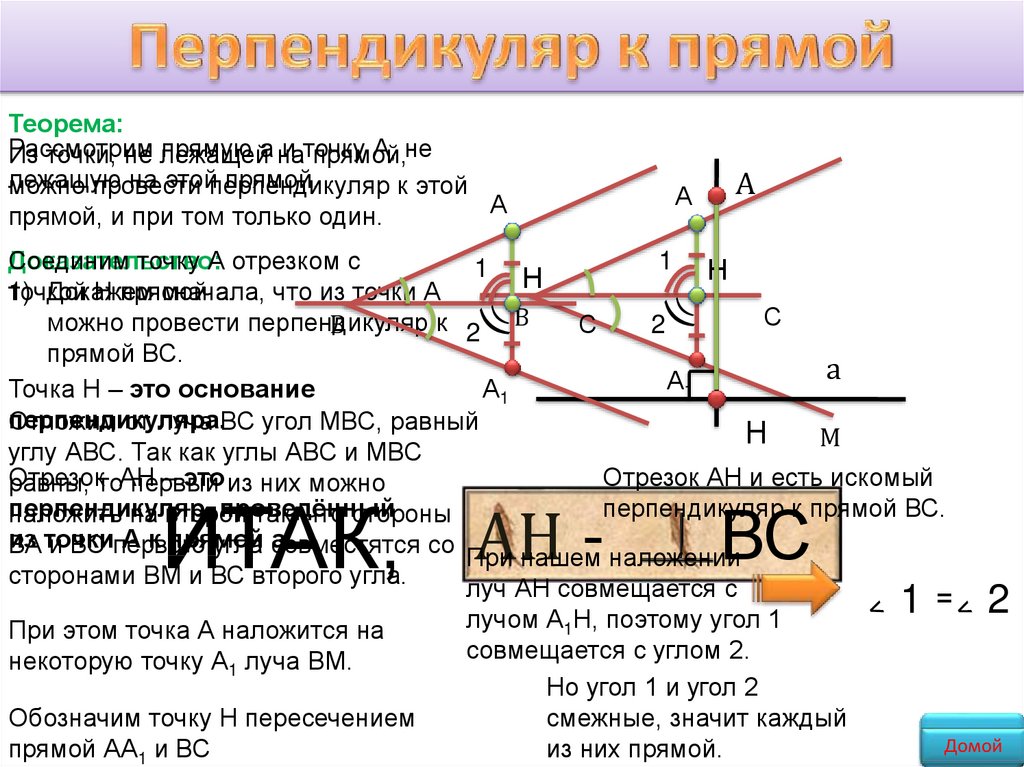
Теорема:
Рассмотрим
прямую а на
и точку
А, не
Из точки, не лежащей
прямой,
лежащую
на этойперпендикуляр
прямой.
можно провести
к этой
А
прямой, и при том только один.
А
А
Соединим точку А отрезком с
Доказательство:
1 Н
1 Н
1) Докажем
точкой
Н прямой
сначала,
а. что из точки А
С
можно провести перпендикуляр
к 2 В
В
С
2
прямой ВС.
а
А1
Точка Н – это основание
А1
перпендикуляра.
Отложим
от луча ВС угол МВС, равный
Н
М
углу АВС. Так как углы АВС и МВС
Отрезок
– это из них можно
Отрезок АН и есть искомый
равны, тоАН
первый
перпендикуляр,
проведённый
перпендикуляр к прямой ВС.
наложить на второй
так, что стороны
из
А к прямой
а.
ВА точки
и ВС первого
угла совместятся
со
При нашем наложении
сторонами ВМ и ВС второго угла.
луч АН совмещается с
= 2
1
лучом А1Н, поэтому угол 1
При этом точка А наложится на
совмещается с углом 2.
некоторую точку А1 луча ВМ.
Но угол 1 и угол 2
смежные, значит каждый
Обозначим точку Н пересечением
Домой
из них прямой.
прямой АА1 и ВС
ИТАК,
АН -
ВС

15.

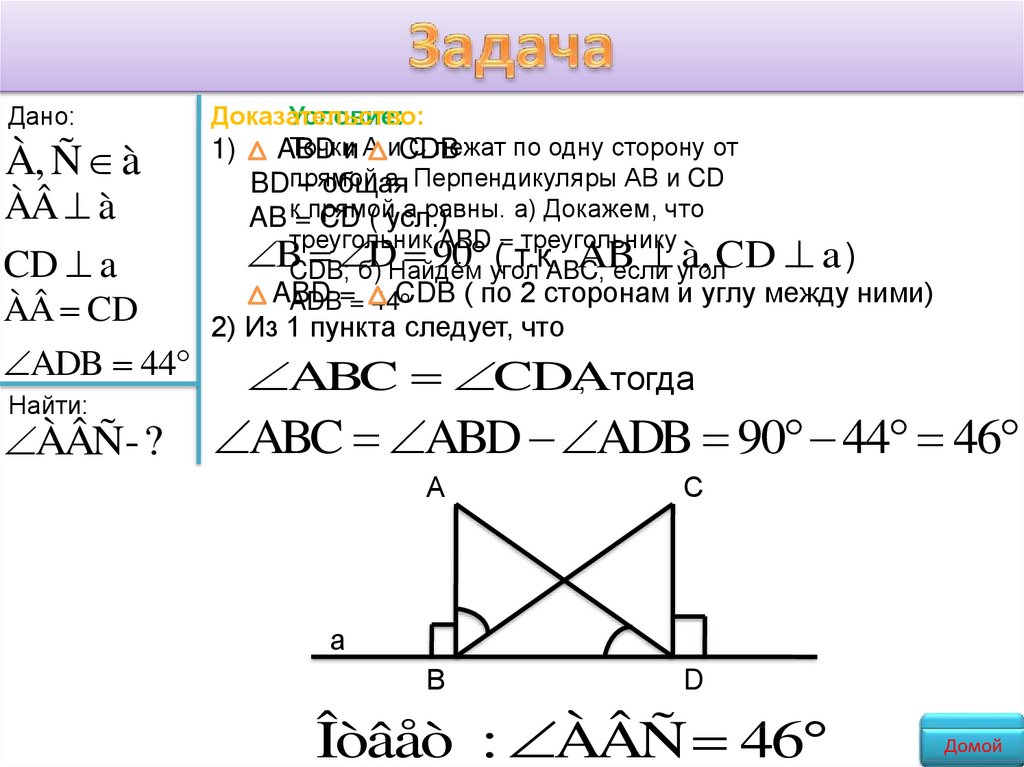
Дано:
À, Ñ à
ÀÂ à
CD a
ÀÂ CD
ADB 44
Найти:
ÀÂÑ- ?
Доказательство:
Условие:
Точкии А иCDB
С лежат по одну сторону от
1) ABD
а. Перпендикуляры АВ и CD
BDпрямой
– общая
а равны. а) Докажем, что
AB к=прямой
CD ( усл.)
треугольник ABD = треугольнику
( т.к.ABC,
BCDB;
б)DНайдём
90 угол
AB
угол
à, CD a )
если
о
ABD
( по 2 сторонам и углу между ними)
ADB== 44CDB
2) Из 1 пункта следует, что
, тогда
ABC CDA
ABC ABD ADB 90 44 46
А
С
В
D
а
Îòâåò : ÀÂÑ 46
Домой

16.

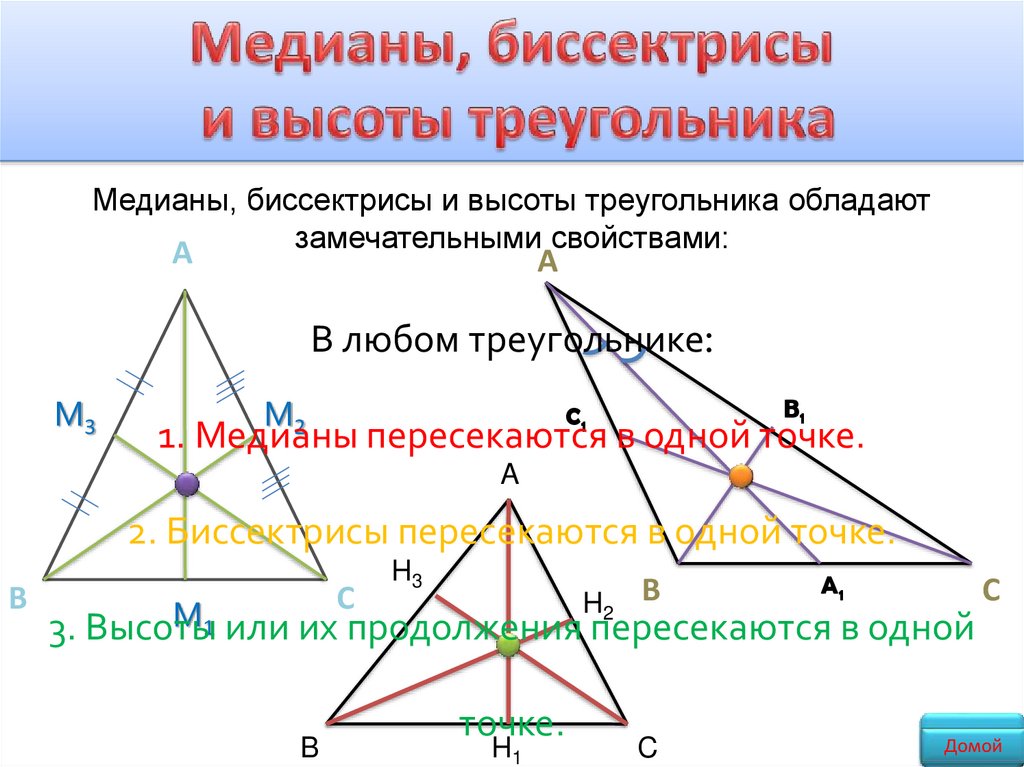
Медианы, биссектрисы и высоты треугольника обладают
замечательными свойствами:
А
А
В любом треугольнике:
M3
M2
B1
C1
1. Медианы пересекаются в одной точке.
A
2. Биссектрисы пересекаются в одной точке.
В
С
H3
H2 В
A1
M1 или их продолжения пересекаются в одной
3. Высоты
B
точке.
H1
C
С
Домой

17.

Дано:
ABC - р\б
AD - биссектриса
ABC =
ACD
Доказательство:
1
(по 1 призн. рав-ва
треугольников)
Пусть AD – биссектриса треугольника
АВС.
AB=AC
Треугольники АВD и ACD равны по
первому признаку равенства
треугольников (АВ=АС по условию, В
AD – общая сторона,
1 = 2,
т.к. AD – биссектриса)
AD – общая сторона
1= 2
Доказать:
В= С
А
Теорема:
В равнобедренном треугольнике
углы при основании равны
2
3 4
D
С
!!!Теорема доказана!!!
В равных треугольниках против
равных сторон, лежат равные углы,
поэтому
В= С
Домой

18.

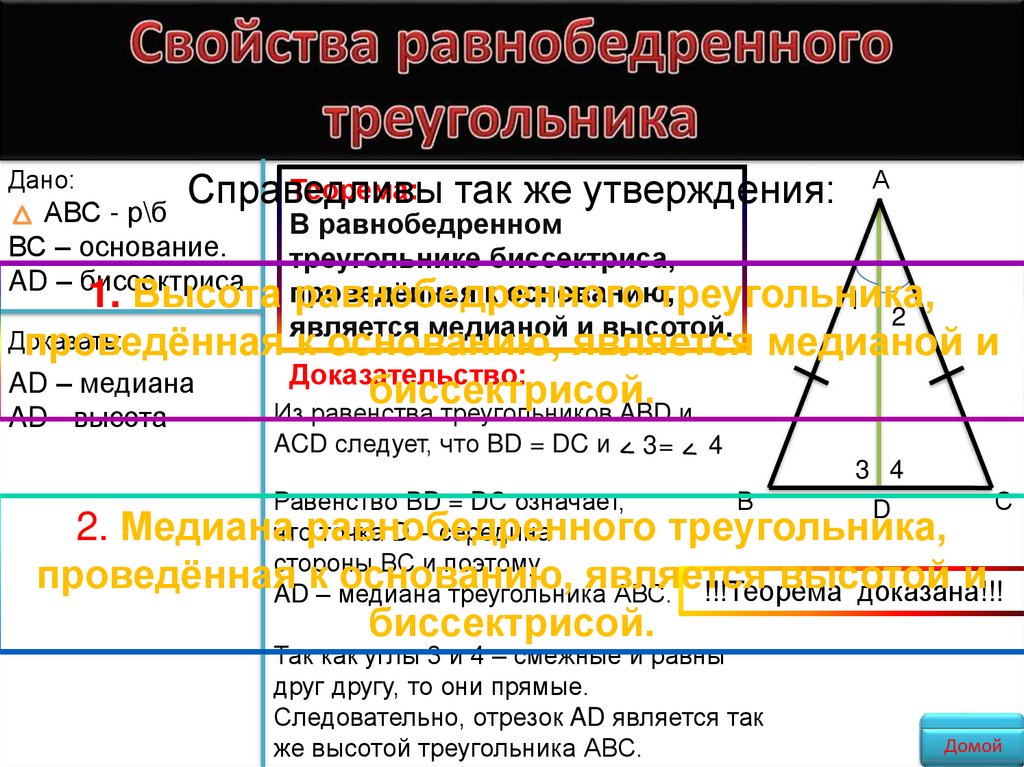
Дано:
Теорема: так же утверждения:
Справедливы
А
АВС - р\б
ВС – основание.
AD – биссектриса.
В равнобедренном
треугольнике биссектриса,
к основанию,
1. Высота проведённая
равнобедренного
треугольника,
1
2
является
медианой
и
высотой.
Доказать:
проведённая к основанию, является медианой и
Доказательство:
AD – медиана
биссектрисой.
Из равенства треугольников ABD и
AD - высота
ACD следует, что BD = DC и
3=
4
3 4
Равенство ВD = DС означает,
В
С
D
2. Медиана
треугольника,
чторавнобедренного
точка D – середина
стороны ВС и поэтому
проведённая
к основанию, является высотой и
AD – медиана треугольника АВС. !!!Теорема доказана!!!
биссектрисой.
Так как углы 3 и 4 – смежные и равны
друг другу, то они прямые.
Следовательно, отрезок AD является так
же высотой треугольника АВС.
Домой

19.

Дано:
АВС
А1В1С1
АВ = А1В1
А = А1
В = В1
Доказать:
АВС = А1В1С1
Теорема:
С
Если сторона и два прилежащих к ней угла
одного треугольника соответственно равны
стороне и двум прилежащим к ней углам
другого треугольника, то такие треугольники
равны.
Доказательство:
А
В
Таким образом, треугольники АВС и А В С полностью
Наложим треугольник АВС на треугольник А1В11С11 1
совместятся,
поэтому
они равны.
В
так, что бы вершина
А совместилась
с вершиной
А,
сторона АВ с равной её стороной А1В1, а вершина
С и С1 оказались по одну сторону от прямой А1В1.
1
1
!!!Теорема доказана!!!
Так как А = А1 и В = В1 , то сторона
АС наложится на луч А1С1, а сторона
ВС – на луч В1С1. Поэтому вершина
С1
С – общая точка сторон
АС и ВС – окажется лежащей как на луче
А1С1, так и на луче В1С1 и, следовательно,
совместится с общей точкой этих лучей –
вершиной С1. Значит совместятся стороны
АС и А1С1, ВС и В1С1
А1
Домой

20.

Дано:
АВС
А1В1С1
АВ = А1В1
ВС = В1С1
СА = С1А1
Доказать:
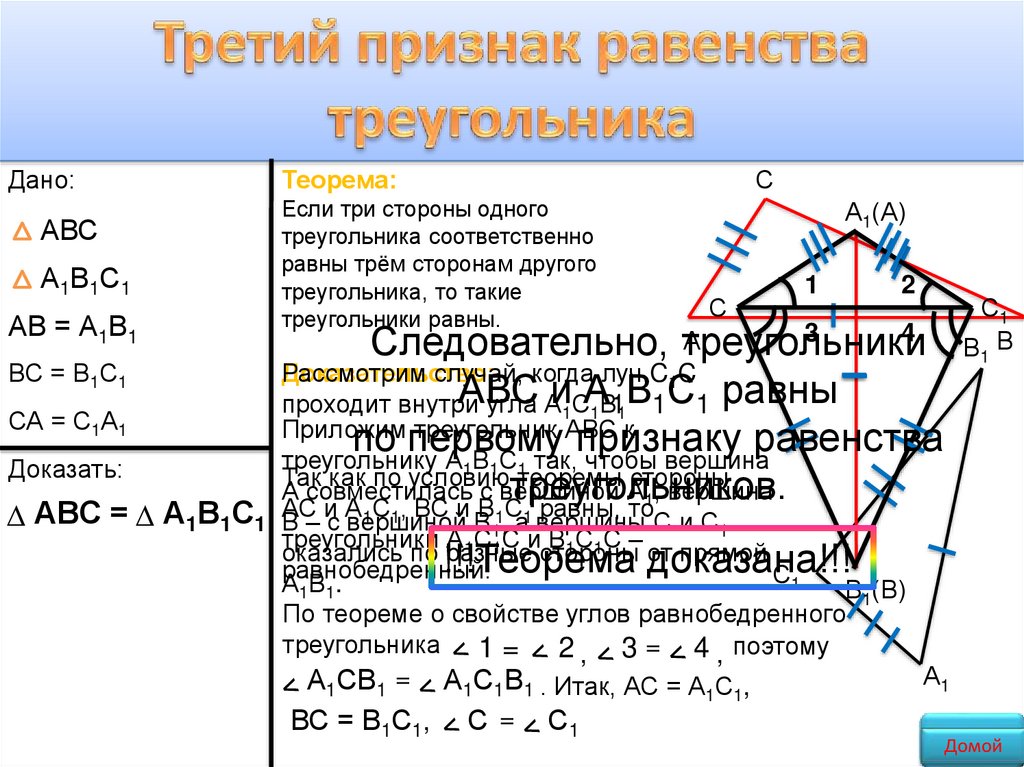
Теорема:
С
Если три стороны одного
треугольника соответственно
равны трём сторонам другого
треугольника, то такие
треугольники равны.
А1(А)
1
С
2
С1
В В
3
4
А
Следовательно, треугольники
Доказательство:
Рассмотрим
случай, когда луч C1C
АВС
В1С1 равны
проходит внутри
угла Аи1СА
1В1
1
Приложим треугольник АВС к
по первому признаку равенства
треугольнику А1В1С1 так, чтобы вершина
Так как по условию теоремы стороны
треугольников.
А совместилась с вершиной
А , вершина
АС и А С , ВС и В С равны, то1
1
1 1
АВС = А1В1С1 В – с вершиной
В11, а1 вершины С и С1
треугольники А1С1С и В1С1С –
оказались по !!!Теорема
разные стороны от
прямой
доказана!!!
равнобедренный.
С1
А1В1.
В1(В)
По теореме о свойстве углов равнобедренного
треугольника 1 =
2 , 3 = 4 , поэтому
А1
А1СВ1 = А1С1В1 . Итак, АС = А С ,
ВС = В1С1,
С =
С1
1
1
Домой

21.

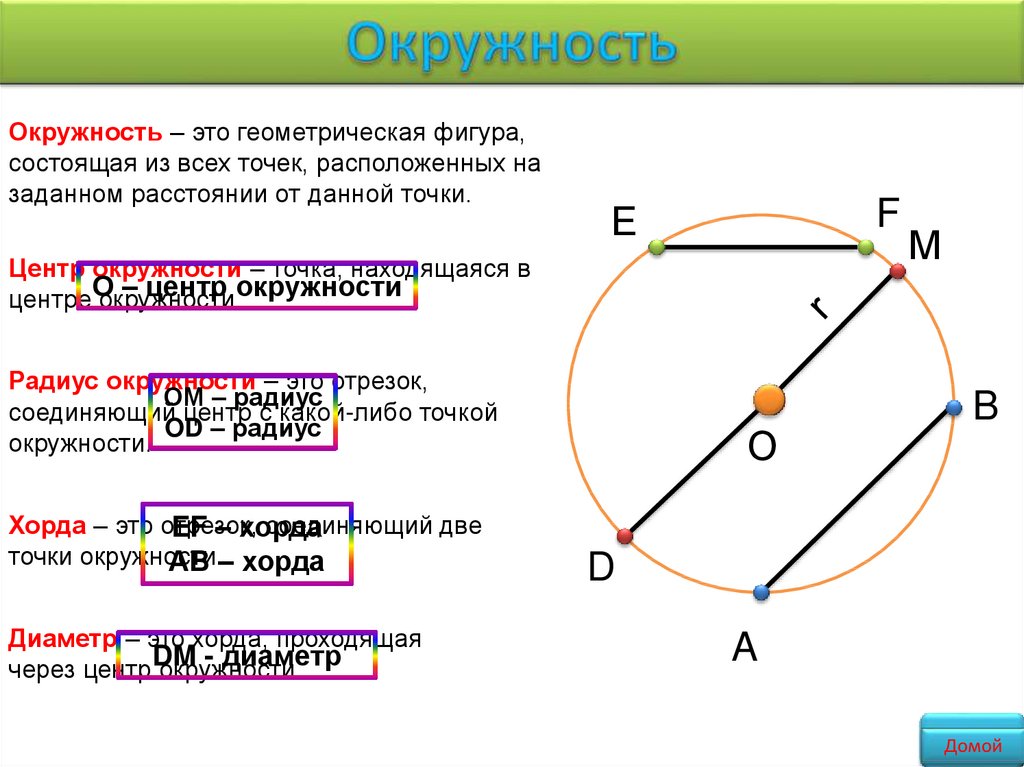
Окружность – это геометрическая фигура,
состоящая из всех точек, расположенных на
заданном расстоянии от данной точки.
F
Е
Центр окружности – точка, находящаяся в
– центр окружности
центреО
окружности.
Радиус окружности – это отрезок,
ОМ – радиус
соединяющий центр с какой-либо точкой
OD – радиус
окружности.
Хорда – это отрезок,
соединяющий две
EF – хорда
точки окружности.
АВ – хорда
Диаметр – это хорда, проходящая
- диаметр
через центрDM
окружности.
О
М
B
D
A
Домой

22.

Домой