Similar presentations:
Треугольник. Решение задач
1.
МБОУ «СОШ №1 г.Суздаля»Учитель математики:
Плотникова Т.В.
2.
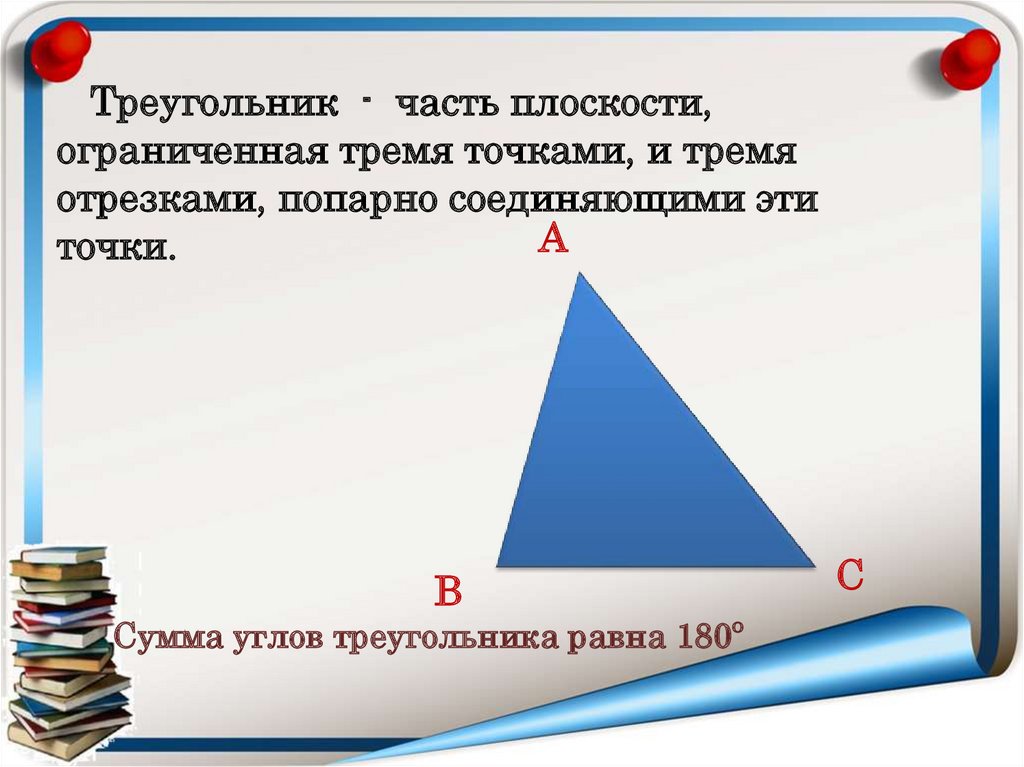
Треугольник - часть плоскости,ограниченная тремя точками, и тремя
отрезками, попарно соединяющими эти
А
точки.
В
Сумма углов треугольника равна 180º
С
3.
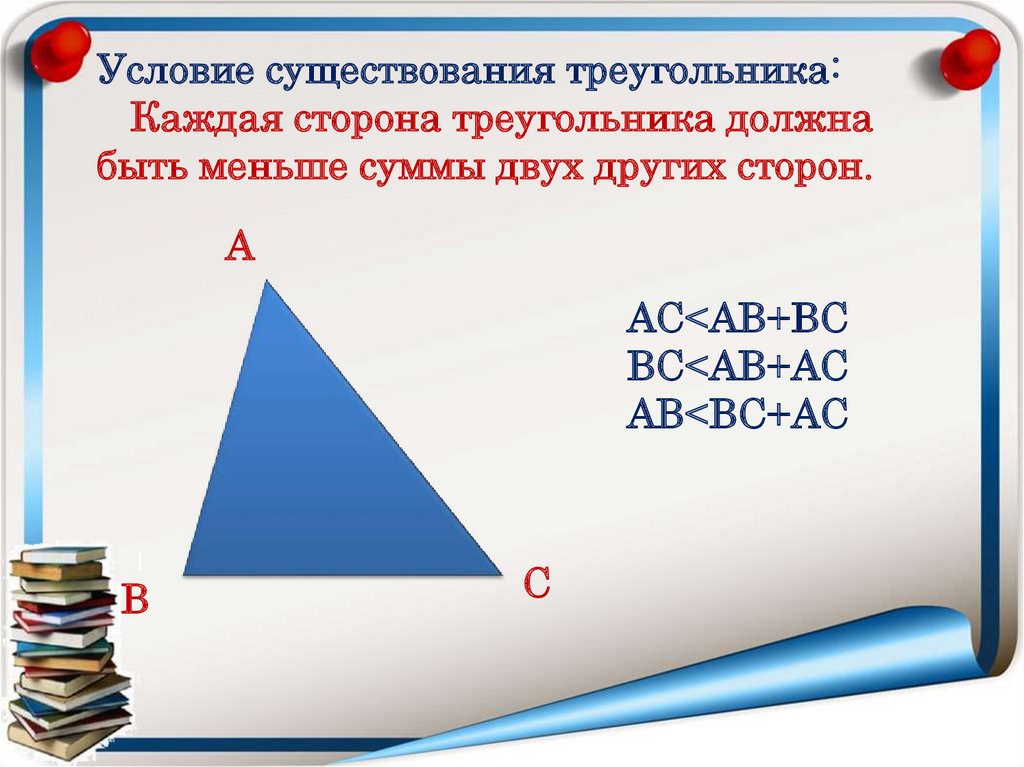
Условие существования треугольника:Каждая сторона треугольника должна
быть меньше суммы двух других сторон.
А
АС<АВ+ВС
ВС<АВ+АС
АВ<ВС+АС
В
С
4.
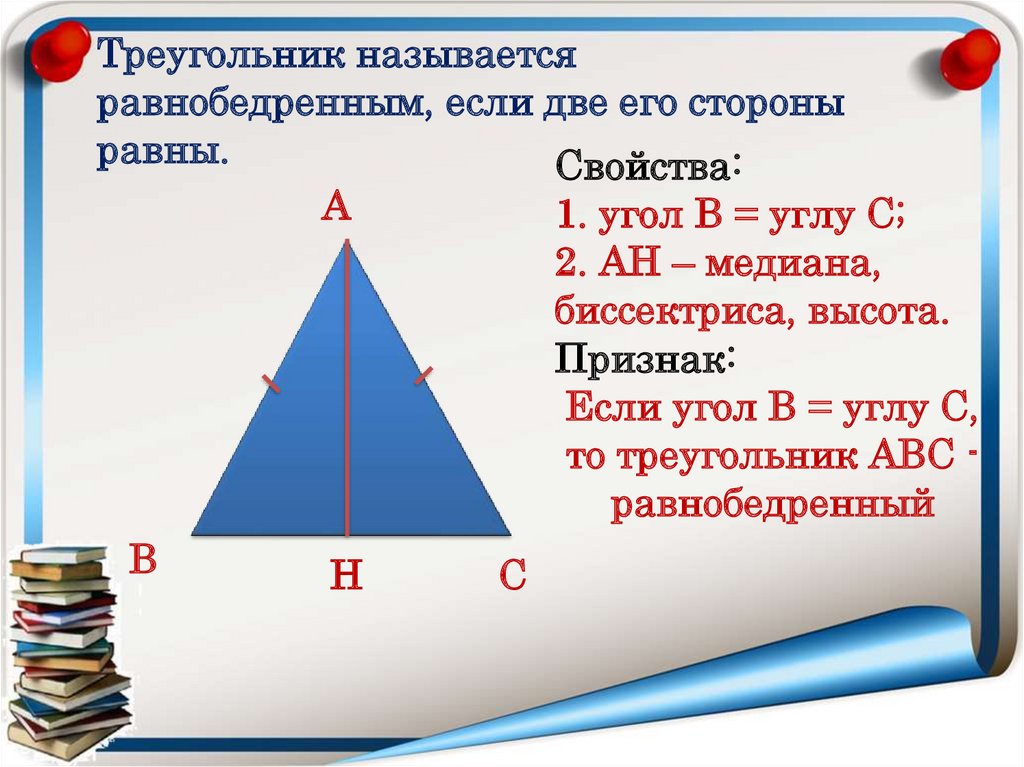
Треугольник называетсяравнобедренным, если две его стороны
равны.
Свойства:
А
1. угол В = углу С;
2. АН – медиана,
биссектриса, высота.
Признак:
Если угол В = углу С,
то треугольник АВС равнобедренный
В
Н
С
5.
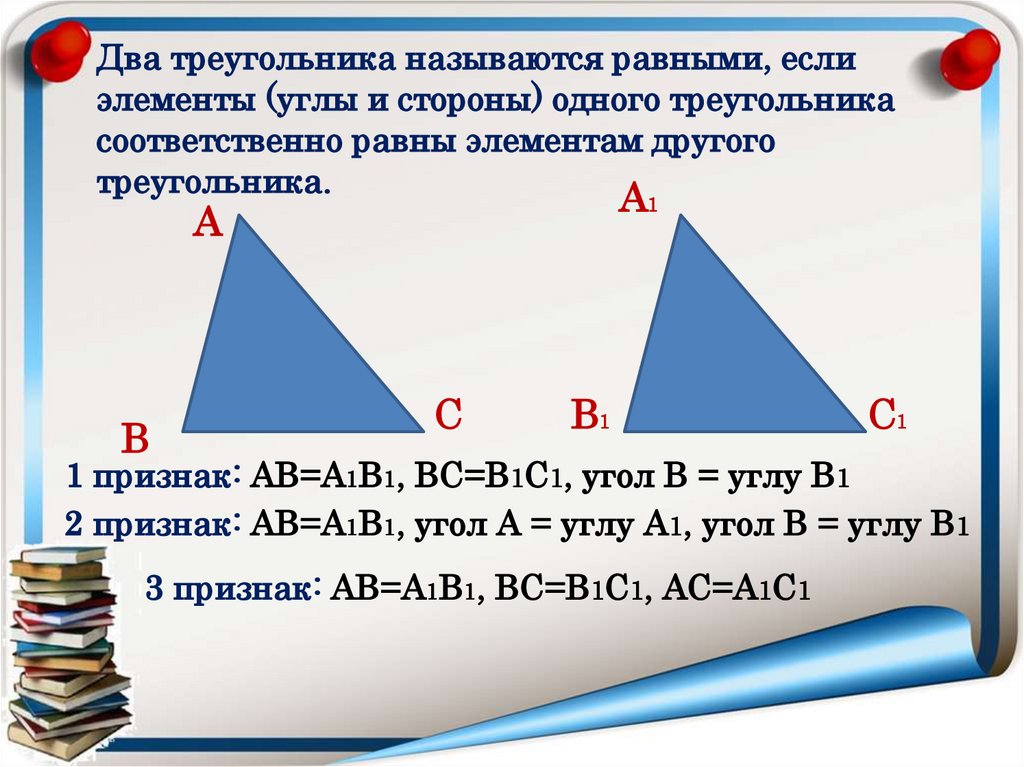
Два треугольника называются равными, еслиэлементы (углы и стороны) одного треугольника
соответственно равны элементам другого
треугольника.
А1
А
В
С
В1
С1
1 признак: АВ=А1В1, ВС=В1С1, угол В = углу В1
2 признак: АВ=А1В1, угол А = углу А1, угол В = углу В1
3 признак: АВ=А1В1, ВС=В1С1, АС=А1С1
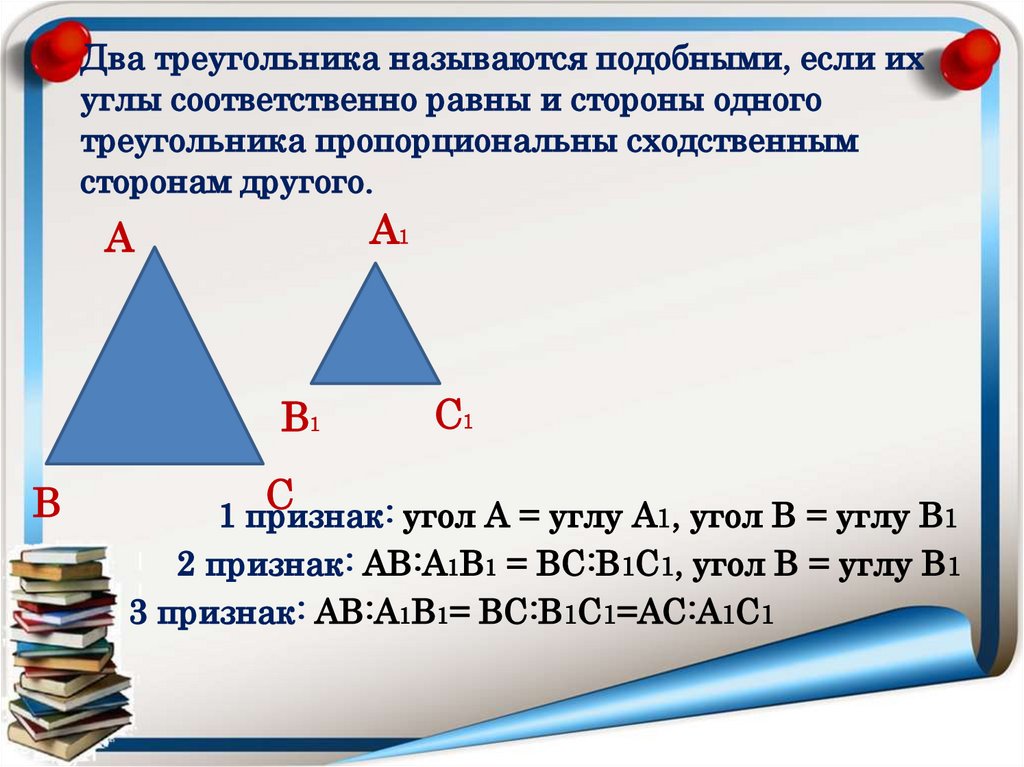
6.
Два треугольника называются подобными, если ихуглы соответственно равны и стороны одного
треугольника пропорциональны сходственным
сторонам другого.
А1
А
В1
В
С
С1
1 признак: угол А = углу А1, угол В = углу В1
2 признак: АВ:А1В1 = ВС:В1С1, угол В = углу В1
3 признак: АВ:А1В1= ВС:В1С1=АС:А1С1
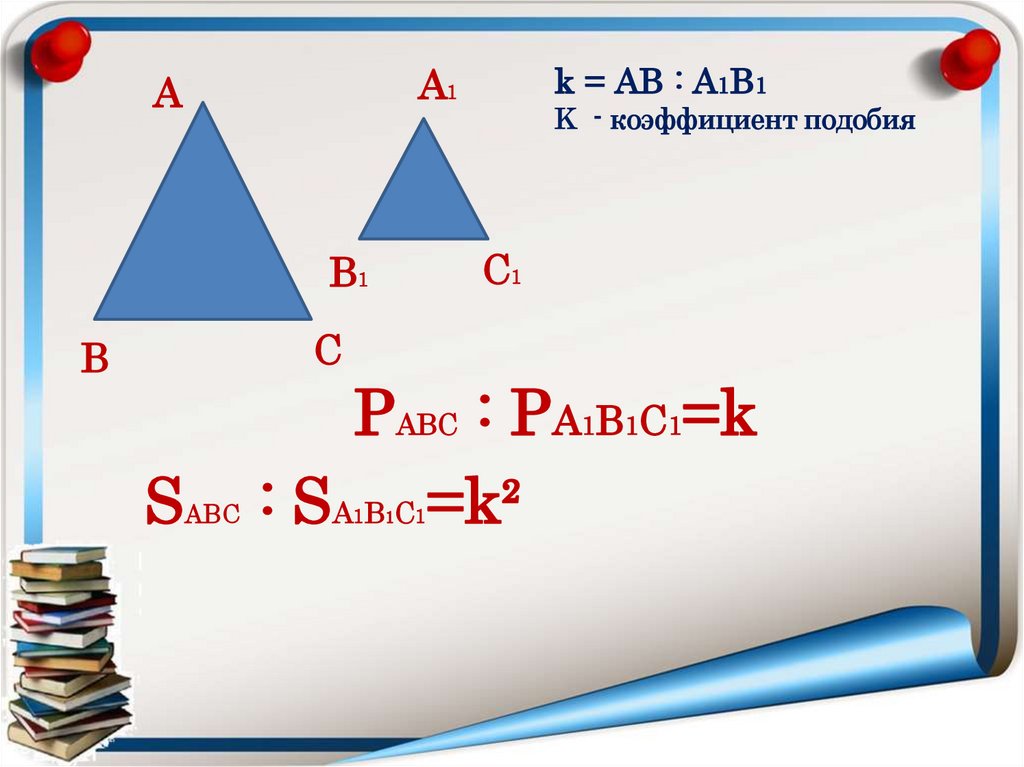
7.
K - коэффициент подобияС1
В1
В
k = АВ : А1В1
А1
А
С
РАВС : РА1В1С1=k
SАВС : SА В С =k²
1
1
1
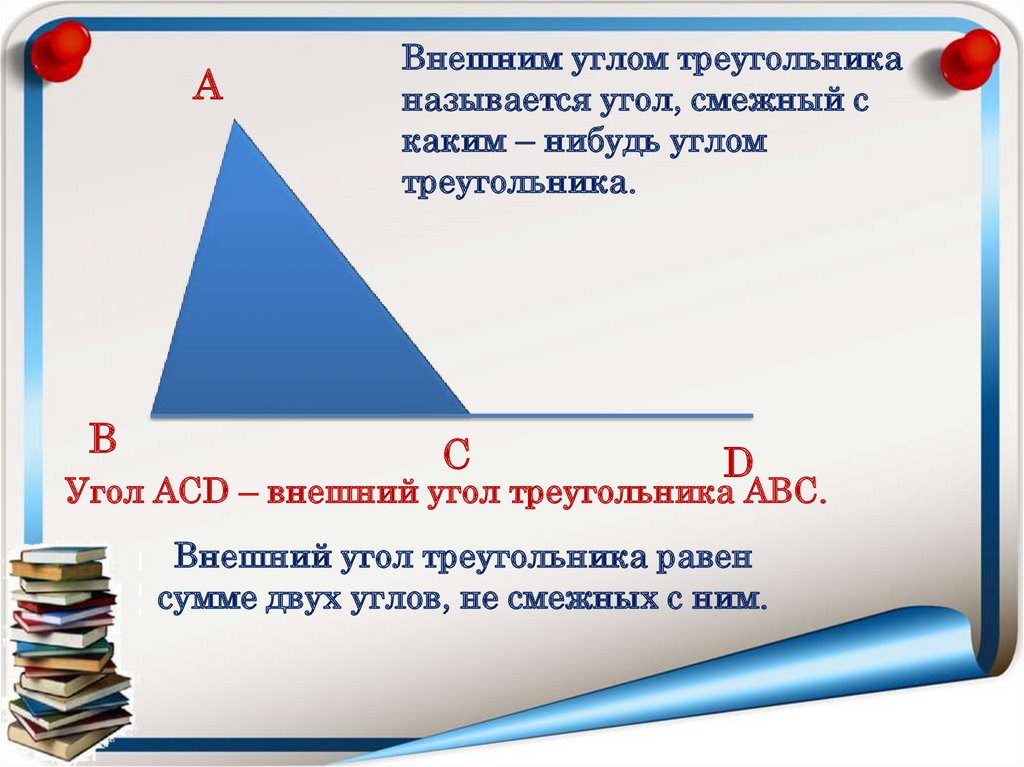
8.
АВ
Внешним углом треугольника
называется угол, смежный с
каким – нибудь углом
треугольника.
С
D
Угол АСD – внешний угол треугольника АВС.
Внешний угол треугольника равен
сумме двух углов, не смежных с ним.
9.
АМ
В
Отрезок, соединяющий середины
двух сторон треугольника,
называется средней линией.
N
Свойство средней линии:
С
МN||ВС,
МN=½ВС
10.
Треугольник, в котором одиниз углов равен 90º, называется
прямоугольным.
А
sin А = СВ:АВ
сos А=АС:АВ
tg А=СВ:АС
С
В
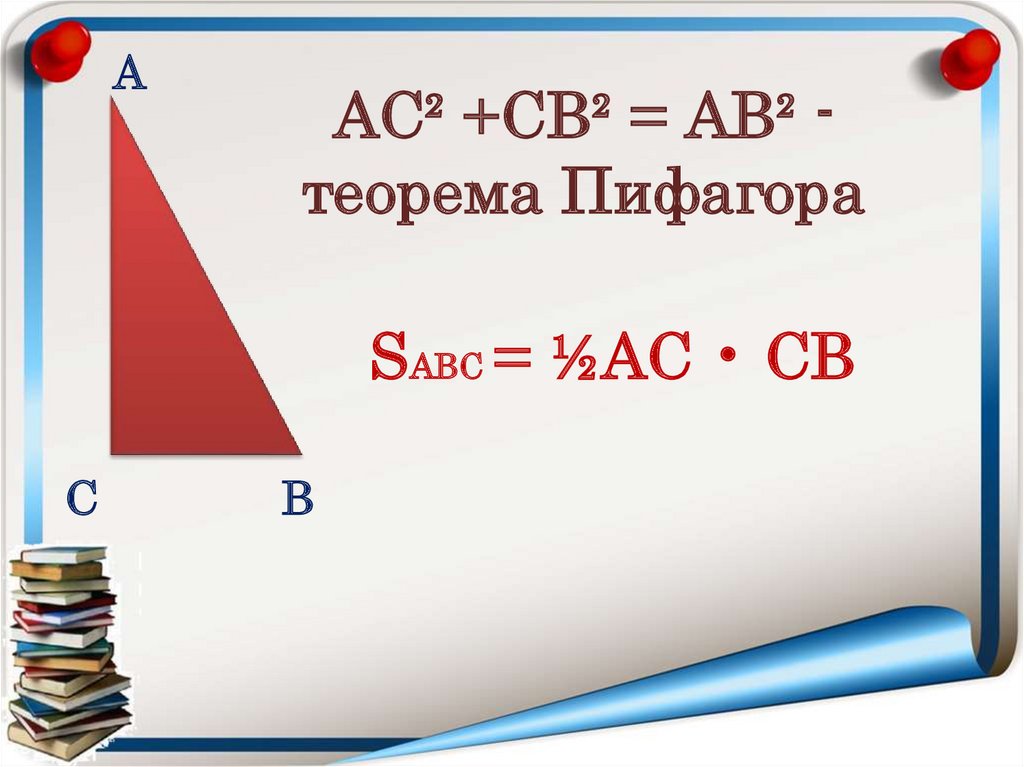
11.
ААС² +СВ² = АВ² теорема Пифагора
SАВС = ½АС • СВ
С
В
12.
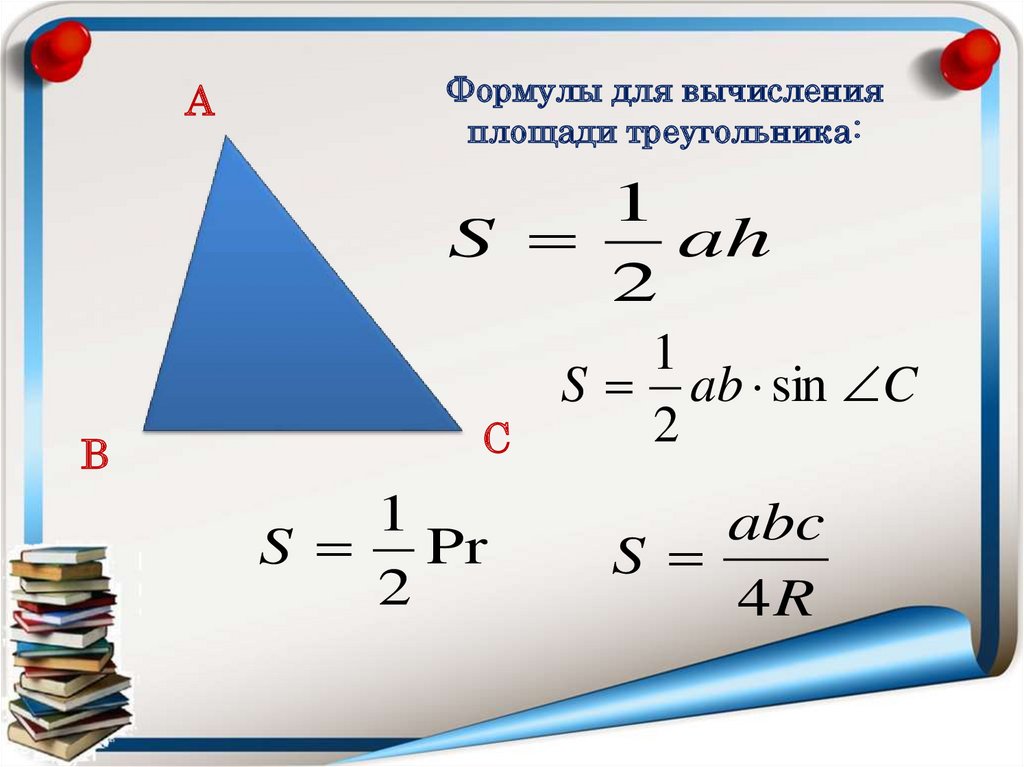
АФормулы для вычисления
площади треугольника:
1
S
ah
2
В
С
1
S Pr
2
1
S ab sin C
2
abc
S
4R
13.
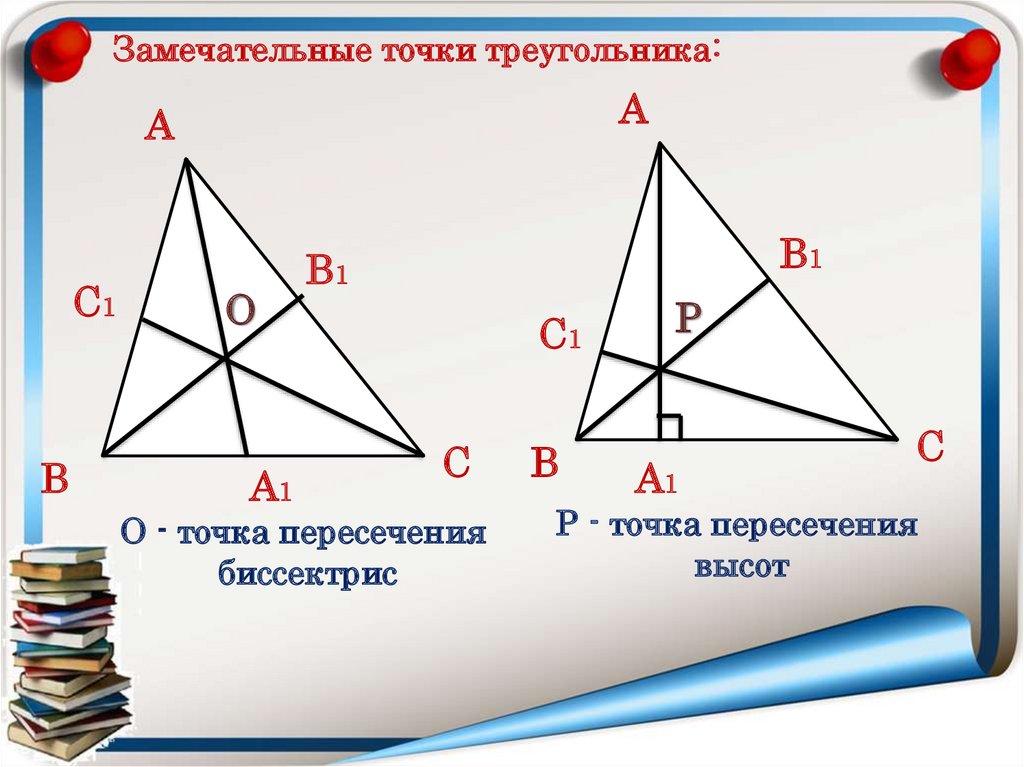
Замечательные точки треугольника:А
А
С1
В
О
А1
В1
В1
С1
С
О - точка пересечения
биссектрис
В
Р
А1
С
Р - точка пересечения
высот
14.
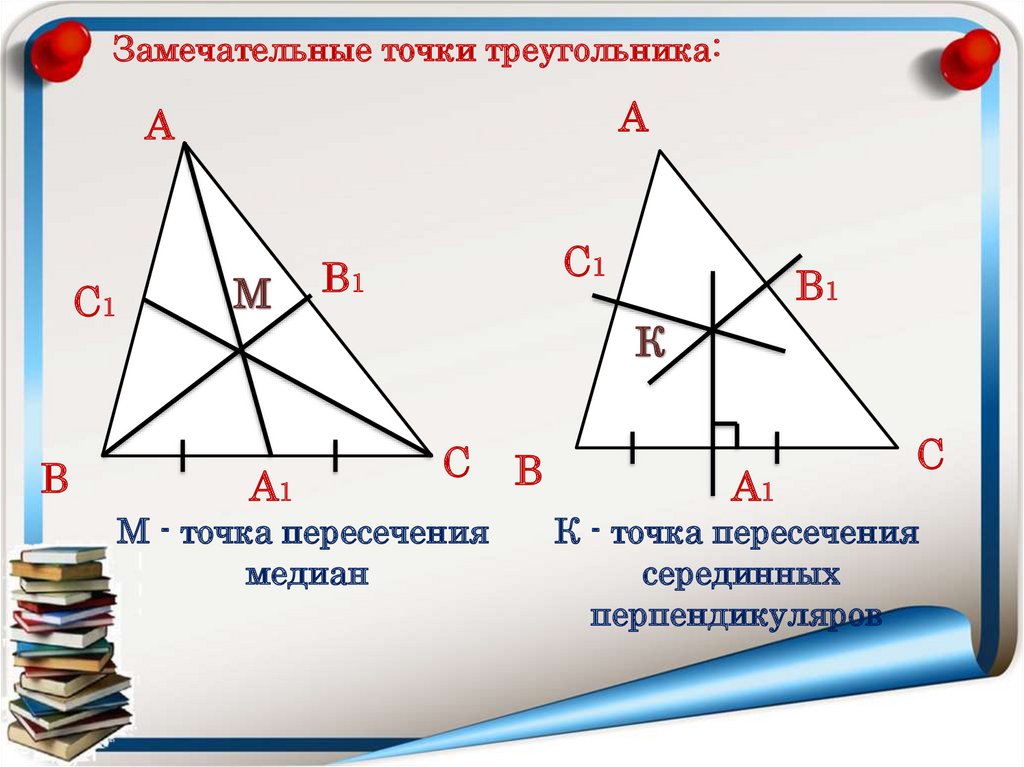
Замечательные точки треугольника:А
А
С1
В
М
С1
В1
В1
К
А1
С
М - точка пересечения
медиан
В
А1
С
К - точка пересечения
серединных
перпендикуляров
15.
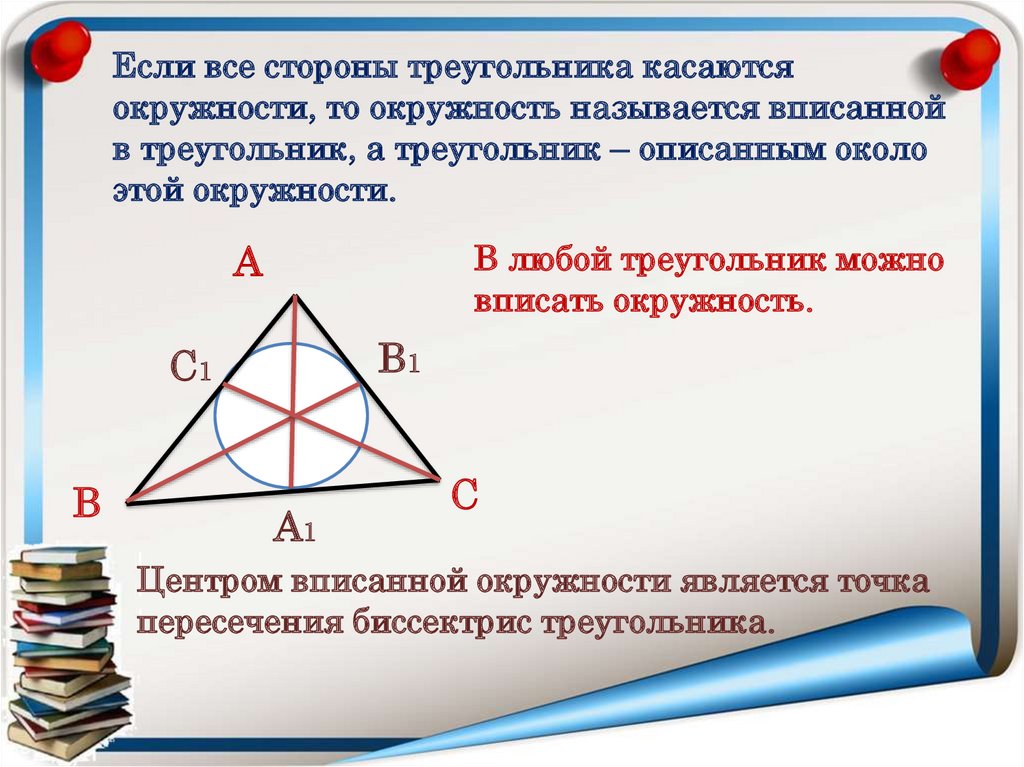
Если все стороны треугольника касаютсяокружности, то окружность называется вписанной
в треугольник, а треугольник – описанным около
этой окружности.
В любой треугольник можно
вписать окружность.
А
В1
С1
В
А1
С
Центром вписанной окружности является точка
пересечения биссектрис треугольника.
16.
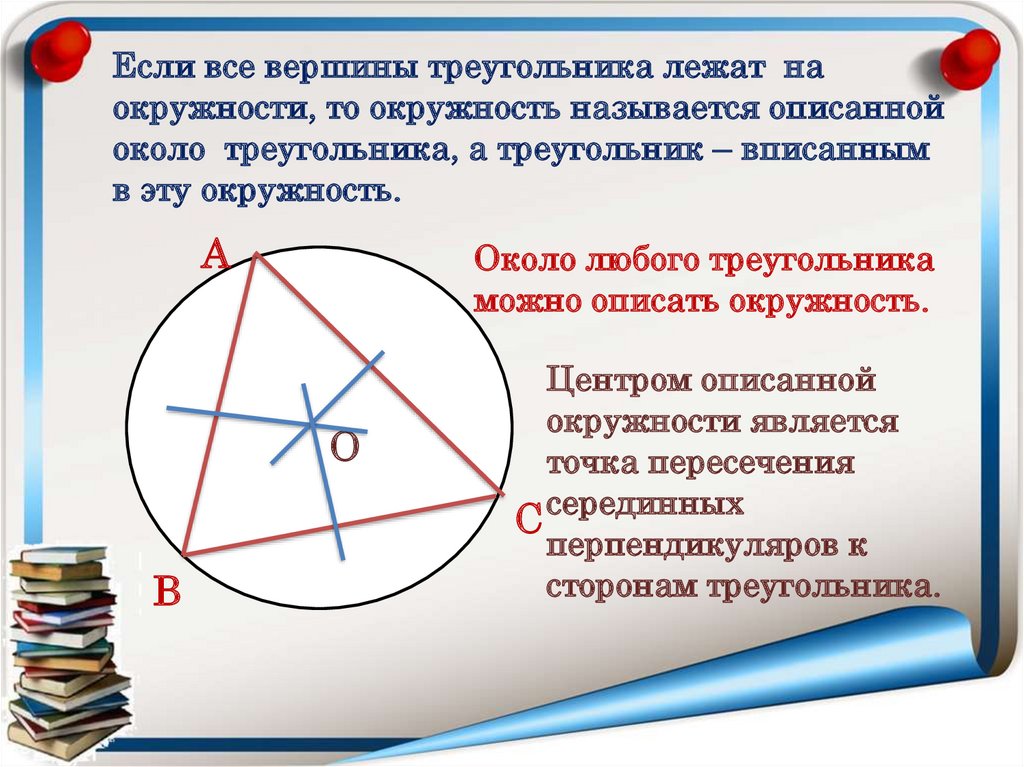
Если все вершины треугольника лежат наокружности, то окружность называется описанной
около треугольника, а треугольник – вписанным
в эту окружность.
А
Около любого треугольника
можно описать окружность.
О
В
Центром описанной
окружности является
точка пересечения
С серединных
перпендикуляров к
сторонам треугольника.
17.
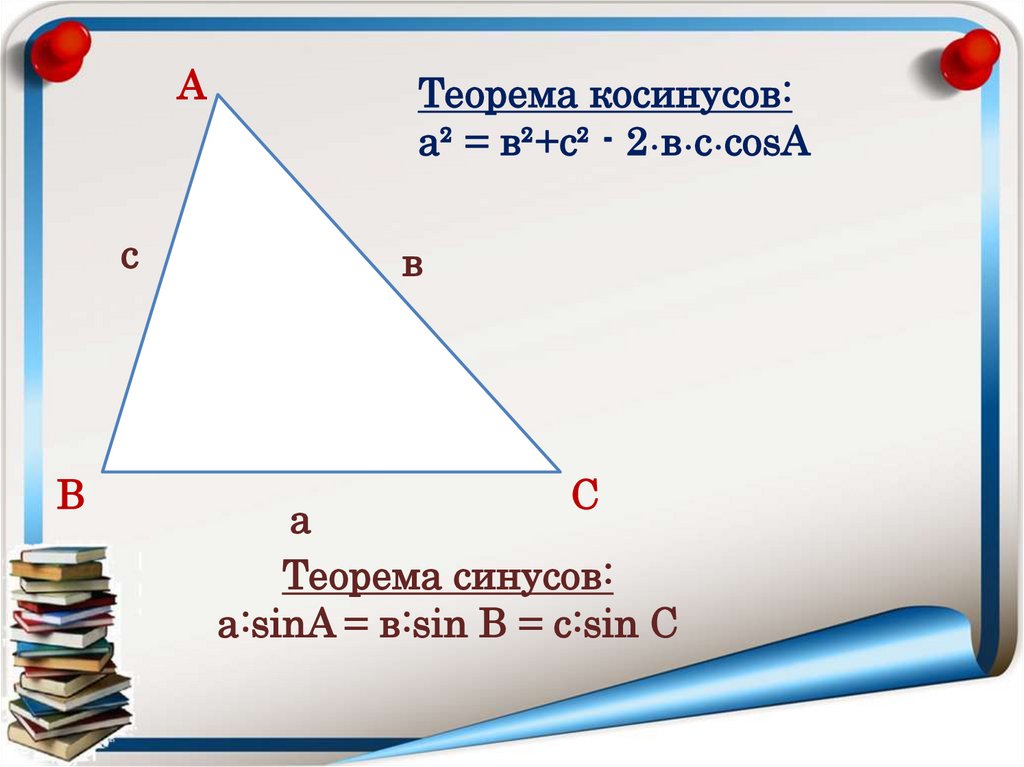
Ас
В
Теорема косинусов:
а² = в²+c² - 2•в•с•cosА
в
С
а
Теорема синусов:
а:sinA = в:sin В = с:sin С
18.
Ответы на письменную работу:«Соотнесите высказывание с его названием
или формулой»
1. д
8. и
2. н
9. г
3. ж
10. т
4. м
11. п
5. б
12. р
6. е
13. л
7. з
14. в
19. Источники использованных изображений:
http://s58.radikal.ru/i162/1007/2d/0d2c12b4102c.pnghttp://www.rustrahovka.ru/upload/iblock/b8c/.png
http://www.grafamania.net/uploads/posts/200808/1219611582_7.jpg
http://intoclassics.net/_nw/175/s49938722.jpg





 mathematics
mathematics








