Треугольники. Планиметрия

1.

Задание 3
Планиметрия
Часть 1. Треугольники

2.

Рекомендации ученикам
По каждой теме:
1. Изучайте презентацию, смотрите
видеоролики.
2. Решайте самостоятельную работу
После изучения всех тем – решайте подборку
задач из ЕГЭ прошлых лет.
Задачи из банка ФИПИ решайте в течение года

3.

Задание 3. План изучения темы
1. Треугольники
1.
2.
3.
Прямоугольный треугольники
Равнобедренный треугольник
Произвольный треугольник
2. Четырехугольники
1. Трапеция
2. Параллелограмм и ромб
3. Прямоугольник и квадрат
3. Окружность и углы
4. Вписанные и описанные окружности
1.
2.
3.
Окружность + треугольник
Окружность + четырехугольник
Окружность + шестиугольник

4.

1.1. Прямоугольный треугольник
a, b - катеты
с - гипотенуза
c
а
sin =
противолежащий катет
гипотенуза
=
a
c
=
b
c
b
a
b
c
ctg =
cos =
tg =
прилежащий катет
гипотенуза
противолежащий катет
прилежащий катет
противолежащий катет
прилежащий катет
=
b
a
=
a
b

5.

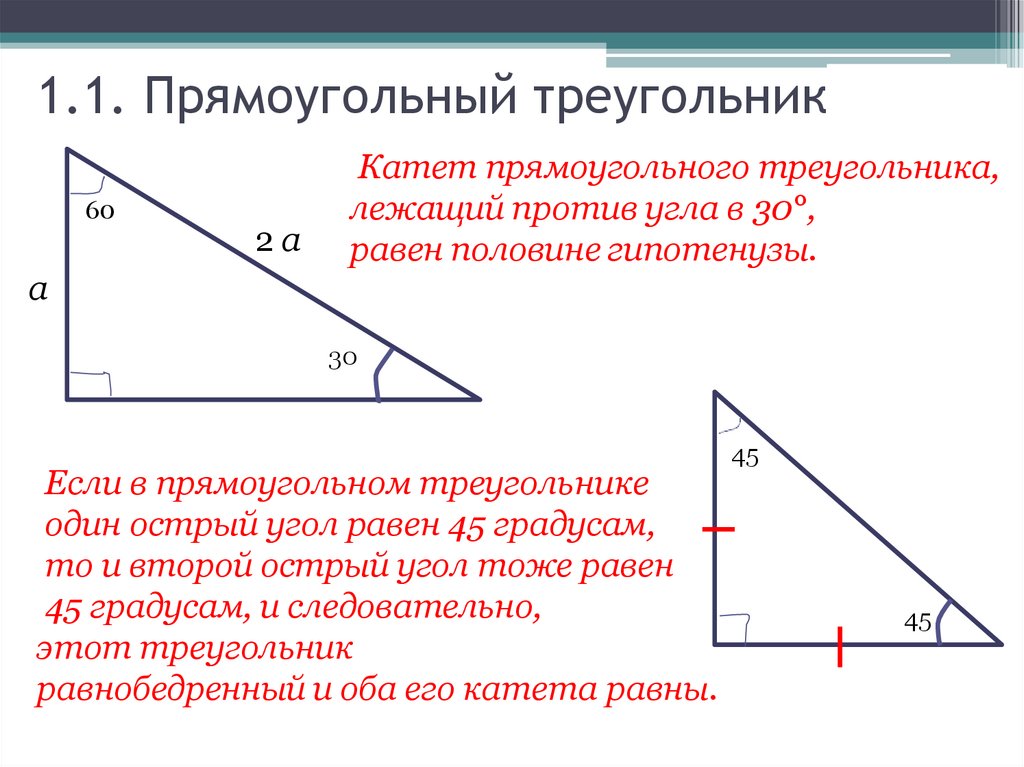
1.1. Прямоугольный треугольник
60
2a
Катет прямоугольного треугольника,
лежащий против угла в 30°,
равен половине гипотенузы.
a
30
Если в прямоугольном треугольнике
один острый угол равен 45 градусам,
то и второй острый угол тоже равен
45 градусам, и следовательно,
этот треугольник
равнобедренный и оба его катета равны.
45
45

6.

1.1. Медиана прямоугольного
треугольника
В прямоугольном треугольнике медиана,
проведённая из вершины прямого угла,
равна половине гипотенузы.
Медиана разбивает прямоугольный
треугольник на два
равнобедренных треугольника

7.

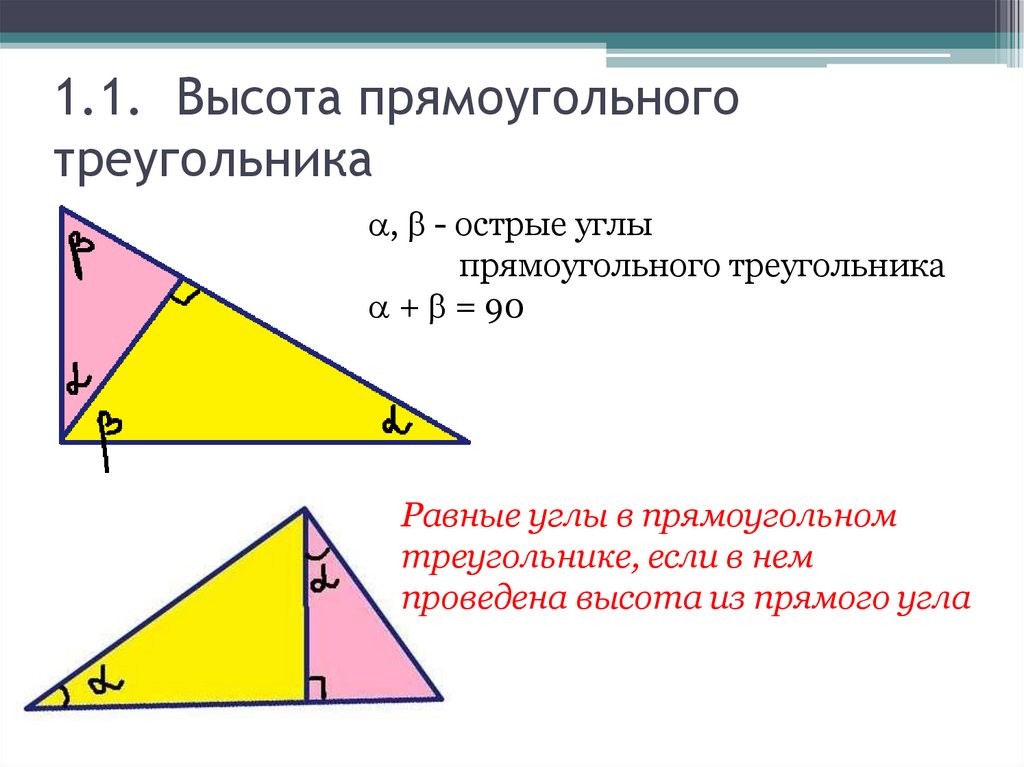
1.1. Высота прямоугольного
треугольника
, - острые углы
прямоугольного треугольника
+ = 90
Равные углы в прямоугольном
треугольнике, если в нем
проведена высота из прямого угла

8.

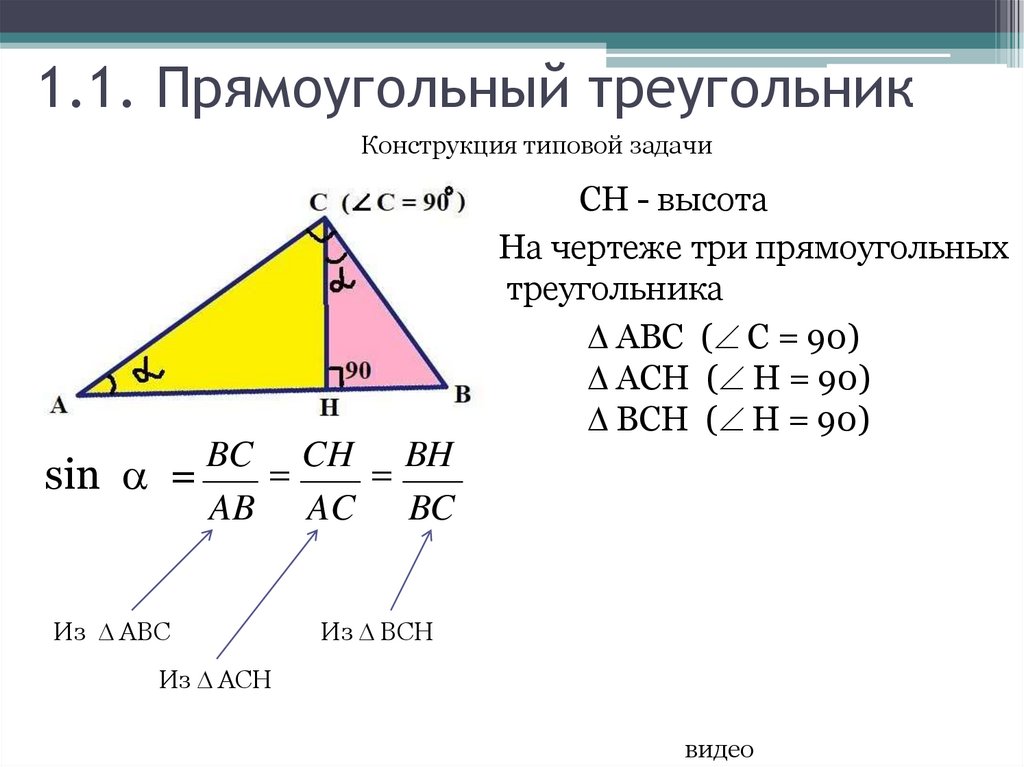
1.1. Прямоугольный треугольник
Конструкция типовой задачи
CH - высота
На чертеже три прямоугольных
треугольника
ABC ( C = 90)
ACH ( H = 90)
BCH ( H = 90)
sin =
BC CH BH
AB AC BC
Из АВС
Из BCH
Из АСH
видео

9.

1.1. Взаимосвязь тригонометрических
функций
Например, вам известен
тангенс,
а хотите найти косинус
tg = 3
cos - ?
Есть два способа
2 способ
С помощью прямоугольного
треугольника
1 способ
Тригонометрические
формулы
sin 2 cos 2 1
1
cos 2
sin
tg
cos
1 tg 2
32 1 2 10
sin
3
1
3
10
1
cos
10

10.

1.1. Прямоугольный треугольник
1 5 26
sin
1
5
cos
2
1
tg
5
sin
2
BC
AB
26
BC
13
13
26
26
cos CH
CB
26
CH
BC
26
5
(из BCH)
5
1
1
CH
13 / 26
65
1
26 26
CH 2,5

11.

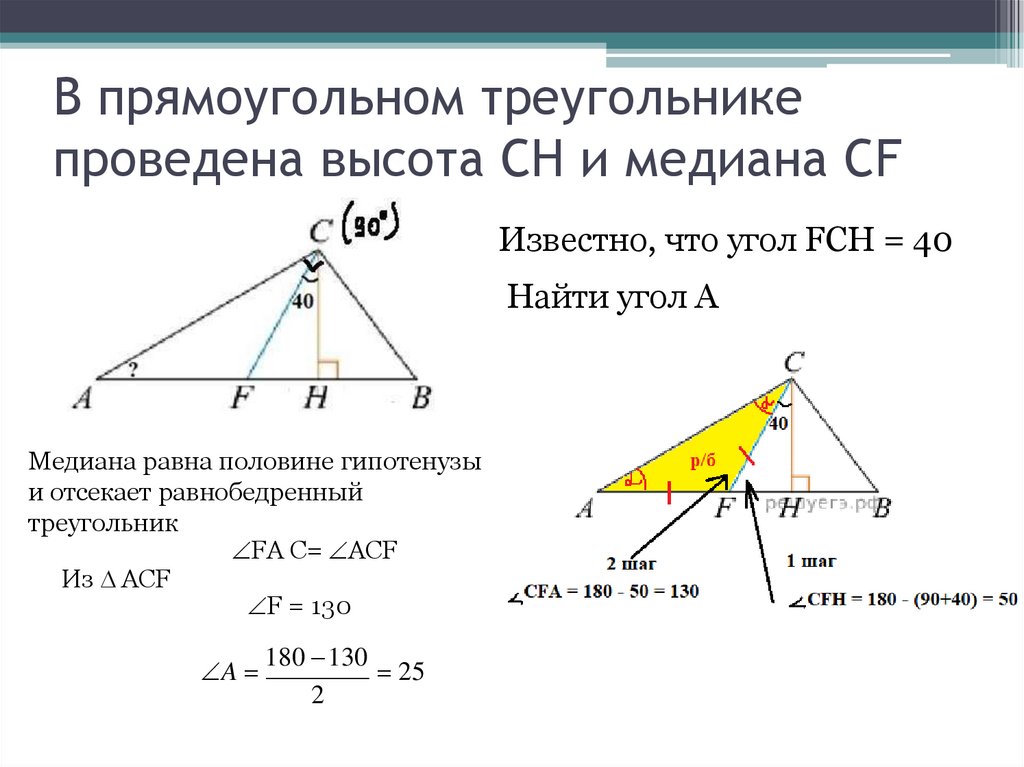
В прямоугольном треугольнике
проведена высота CH и медиана CF
Известно, что угол FCH = 40
Найти угол А
Медиана равна половине гипотенузы
и отсекает равнобедренный
треугольник
FA C= ACF
Из ACF
F = 130
A
180 130
25
2

12.

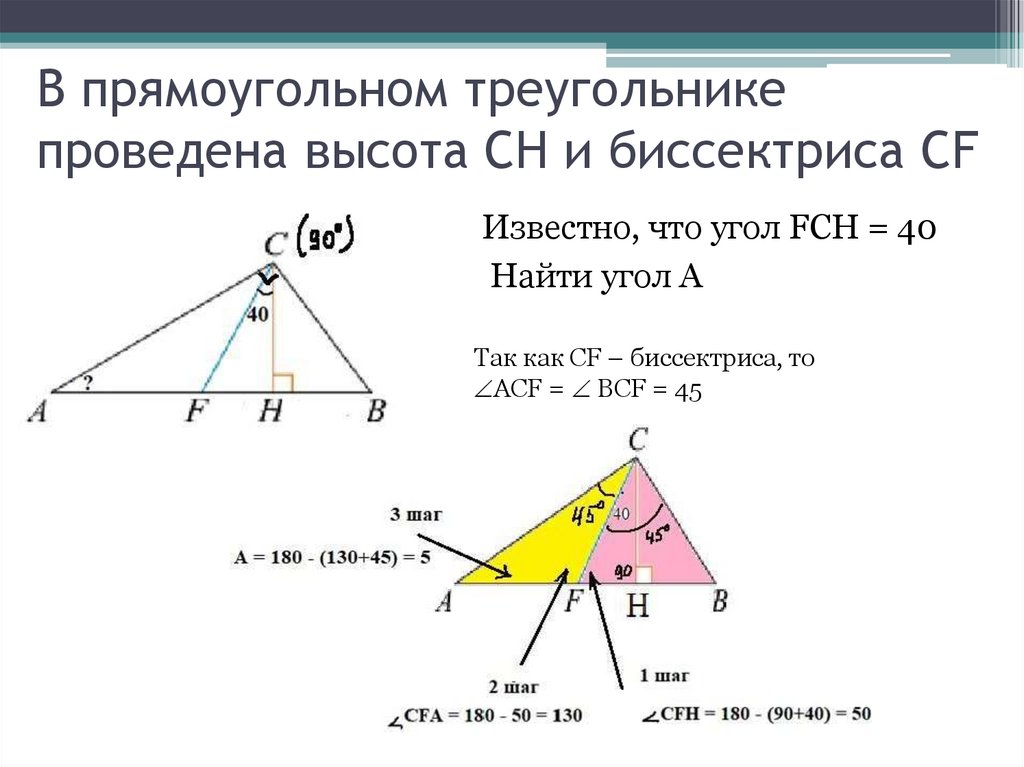
В прямоугольном треугольнике
проведена высота CH и биссектриса CF
Известно, что угол FCH = 40
Найти угол А
Так как CF – биссектриса, то
АСF = BCF = 45

13.

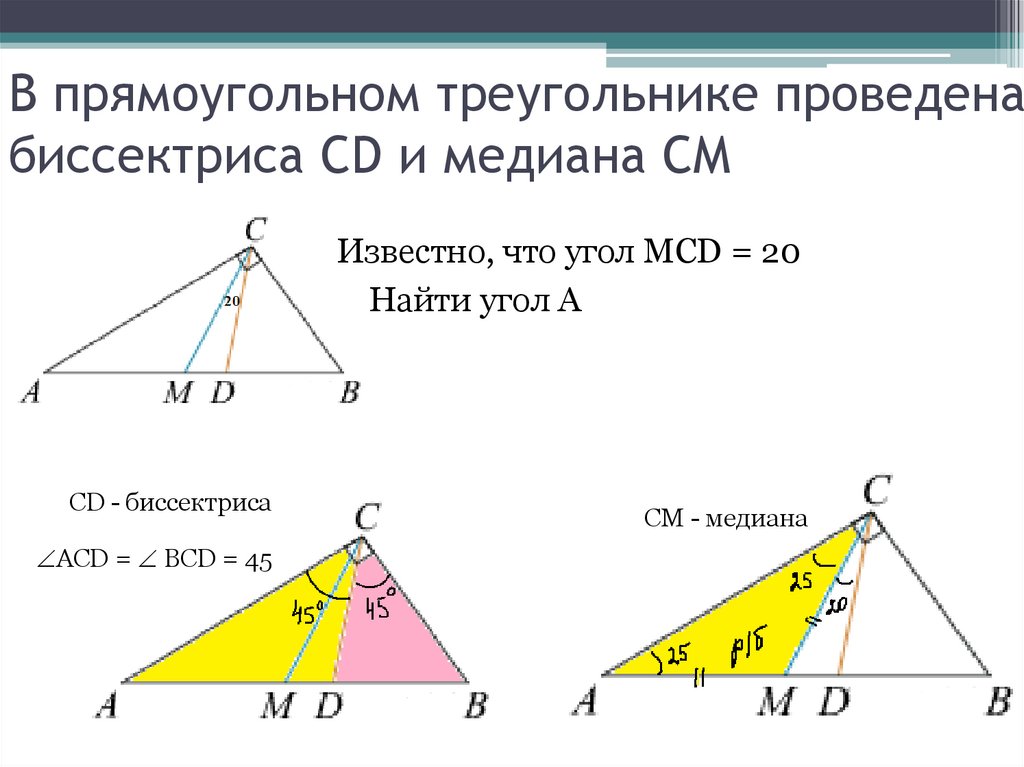
В прямоугольном треугольнике проведена
биссектриса CD и медиана СМ
Известно, что угол MCD = 20
Найти угол А
CD - биссектриса
АСD = BCD = 45
СМ - медиана

14.

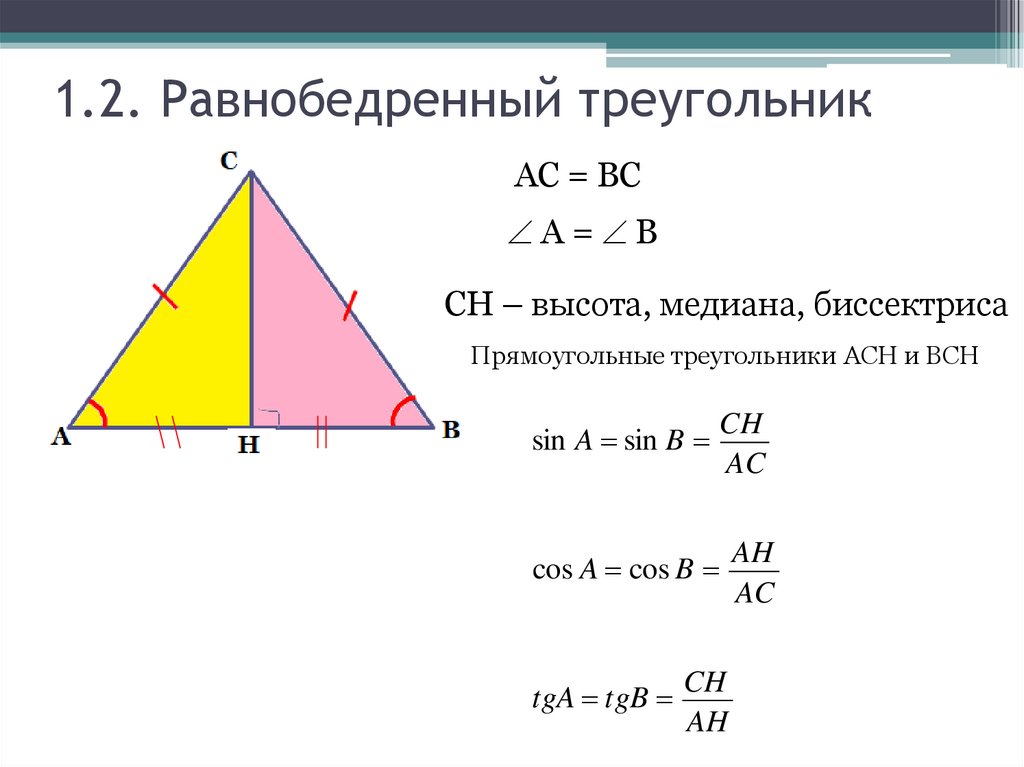
1.2. Равнобедренный треугольник
АС = ВС
А= В
СН – высота, медиана, биссектриса
Прямоугольные треугольники ACH и BCH
sin A sin B
CH
AC
cos A cos B
tgA tgB
CH
AH
AH
AC

15.

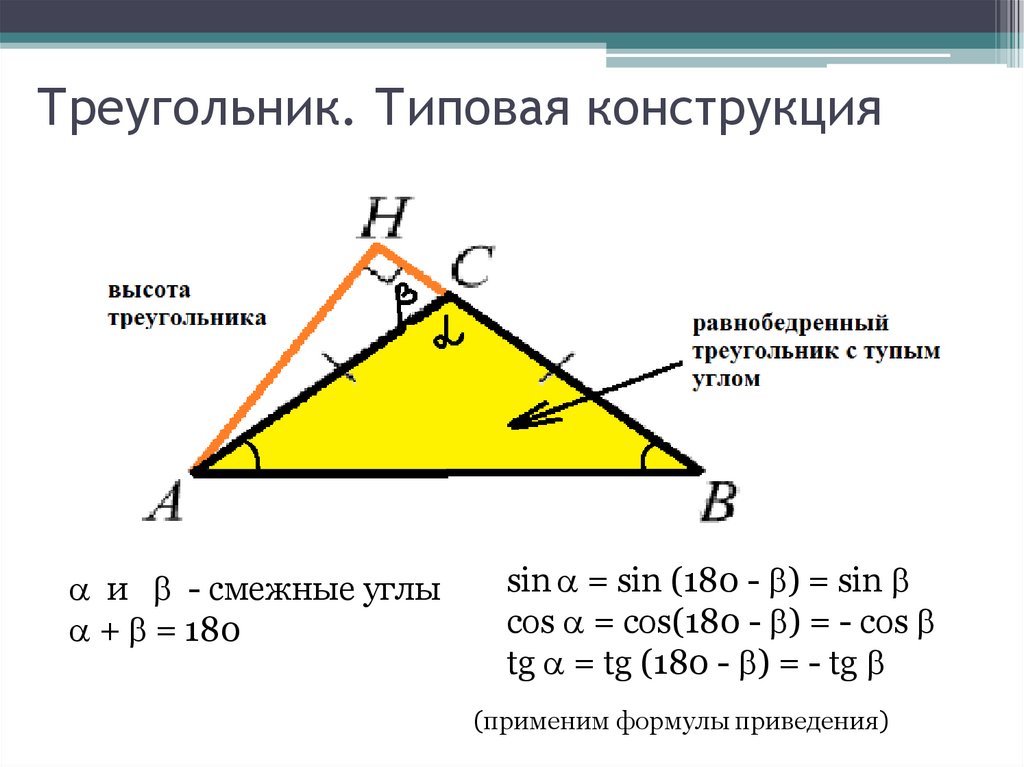
Треугольник. Типовая конструкция
и - смежные углы
+ = 180
sin = sin (180 - ) = sin
cos = cos(180 - ) = - cos
tg = tg (180 - ) = - tg
(применим формулы приведения)

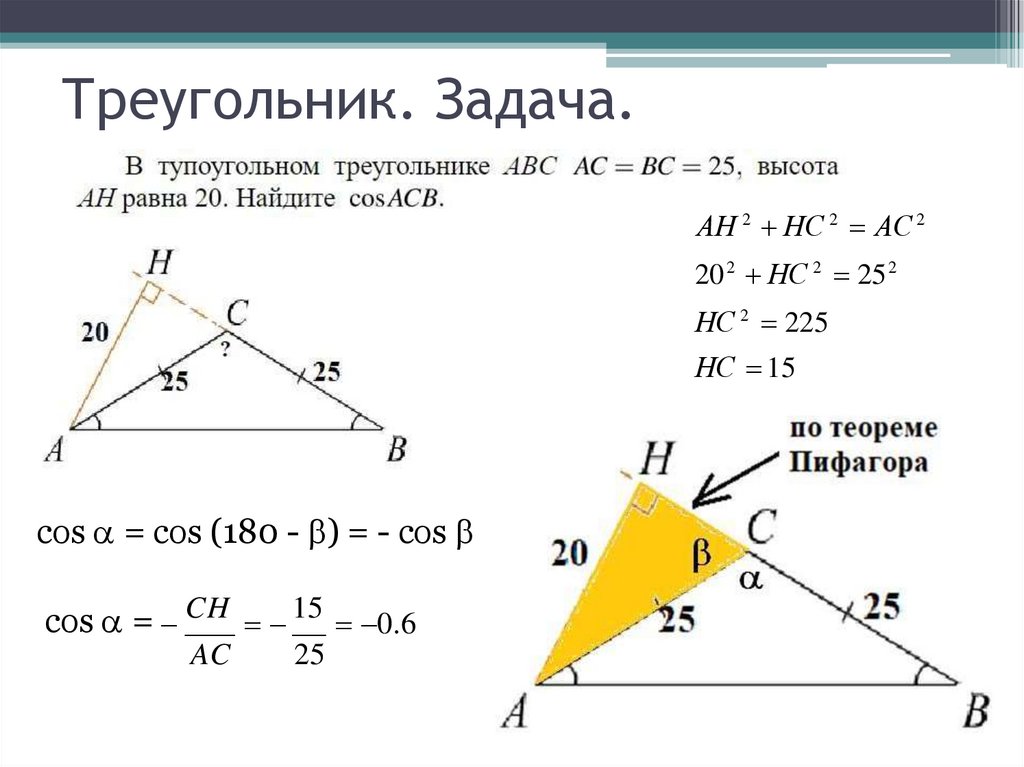
16.

Треугольник. Задача.
АН 2 НС 2 АС 2
20 2 НС 2 25 2
НС 2 225
НС 15
cos = cos (180 - ) = - cos
cos = CH 15 0.6
AC
25

17.

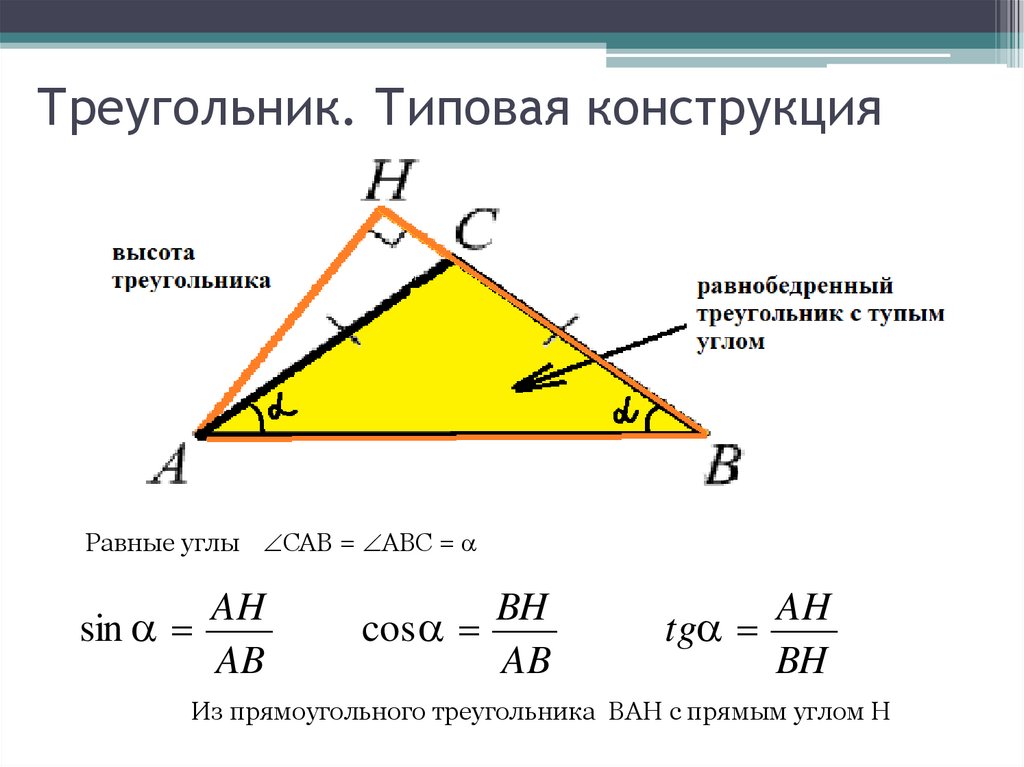
Треугольник. Типовая конструкция
Равные углы САВ = АВС =
AH
sin
AB
BH
cos
AB
AH
tg
BH
Из прямоугольного треугольника BAH c прямым углом Н

18.

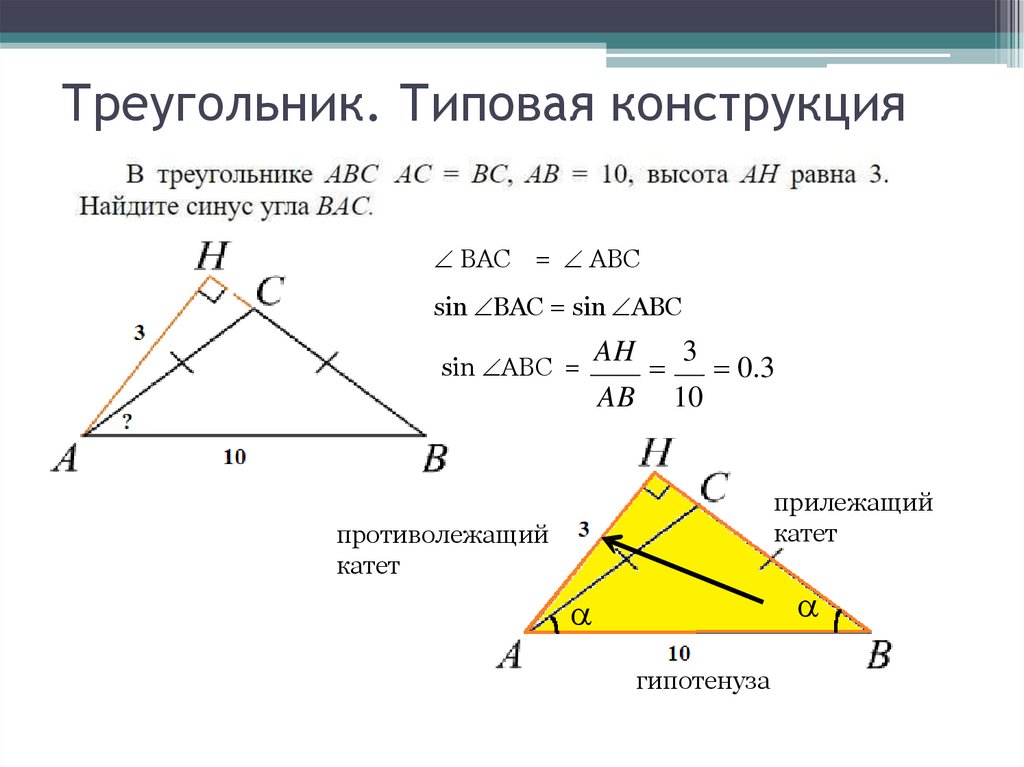
Треугольник. Типовая конструкция
BAC = ABC
sin BAC = sin ABC
sin ABC =
AH
AB
3
0.3
10
прилежащий
катет
противолежащий
катет
гипотенуза

19.

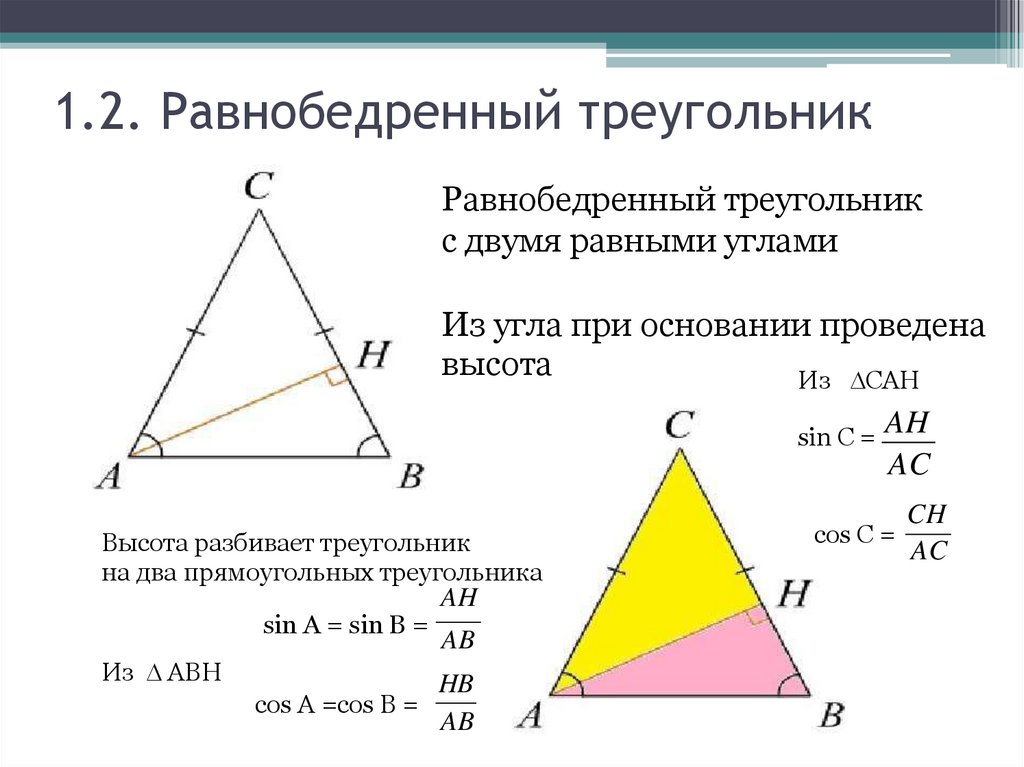
1.2. Равнобедренный треугольник
Равнобедренный треугольник
с двумя равными углами
Из угла при основании проведена
высота
Из CAH
sin C =
Высота разбивает треугольник
на два прямоугольных треугольника
sin A = sin B =
Из ABH
AH
AB
HB
cos A =cos B =
AB
AH
AC
CH
cos C =
AC

20.

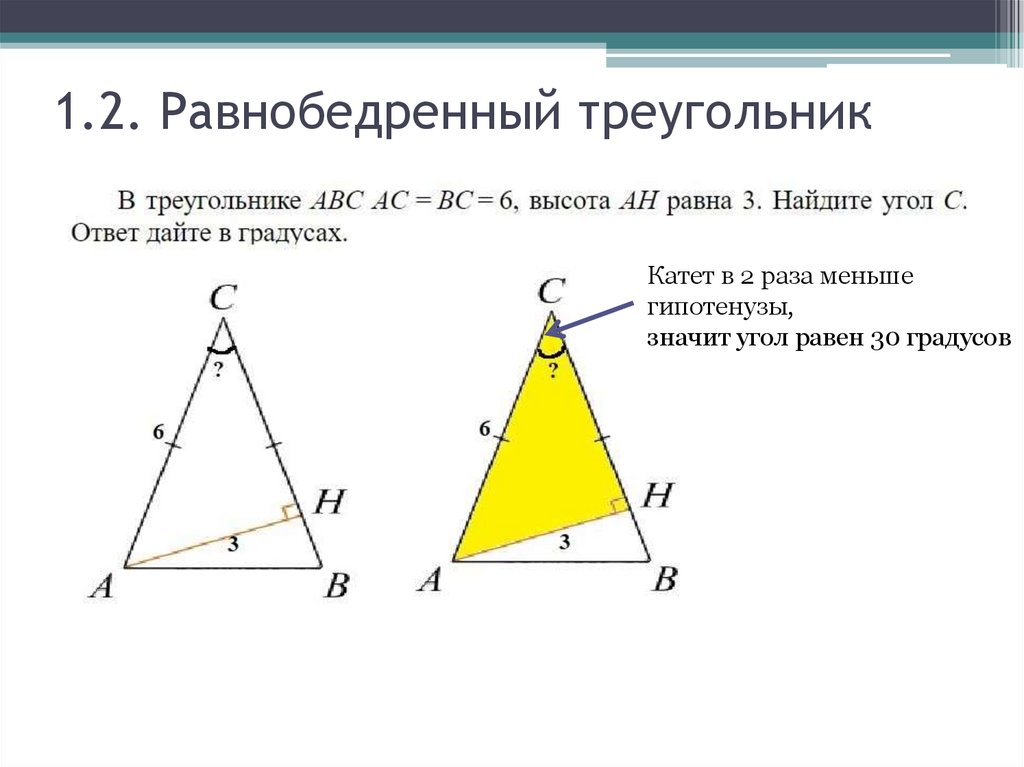
1.2. Равнобедренный треугольник
Катет в 2 раза меньше
гипотенузы,
значит угол равен 30 градусов

21.

1.2. Равнобедренный треугольник
Треугольник равнобедренный, значит углы
при основании равны
AH
33
33
tg B =
tg BAC = tg ABC =
BH
4 33
1 tg 2
1
cos2
4
мы не знаем эти стороны,
найдем значение косинуса
2
33
1
1
cos2
4
49
1
16 cos2
4
cos
7
угол острый, значит берем +
cos
4 BH
7
7
BH 4
BH
AB

22.

Площадь треугольника
Для прямоугольного треугольника
1
S a b
2
а
b
Для произвольного треугольника
1
S a h
2
h
а

23.

Задача. Площадь треугольника
Боковая сторона равнобедренного треугольника
равна 5, а основание равно 6.
Найдите площадь этого треугольника.
1 способ:
32 h 2 5 2
S 1 a h
2
h 4
5
5
S
h
2 способ:
3
3
1
4 6 12
2
Формула Герона
S
p
5 5 6
8
2
p
p ( p a) ( p b) ( p c)
a b c
2
S 8 (8 5) (8 5) (8 6) 8 3 3 2 12

24.

Площадь треугольника
1
S a b sin
2
а
b
Угол при вершине, противолежащей основанию равнобедренного
треугольника, равен 150°.
20
Боковая сторона треугольника равна 20.
20
150
Найдите площадь этого треугольника.
S
1
2
20 20 sin 150 200 sin(180 30) 200 sin 30 200
1
2
100

25.

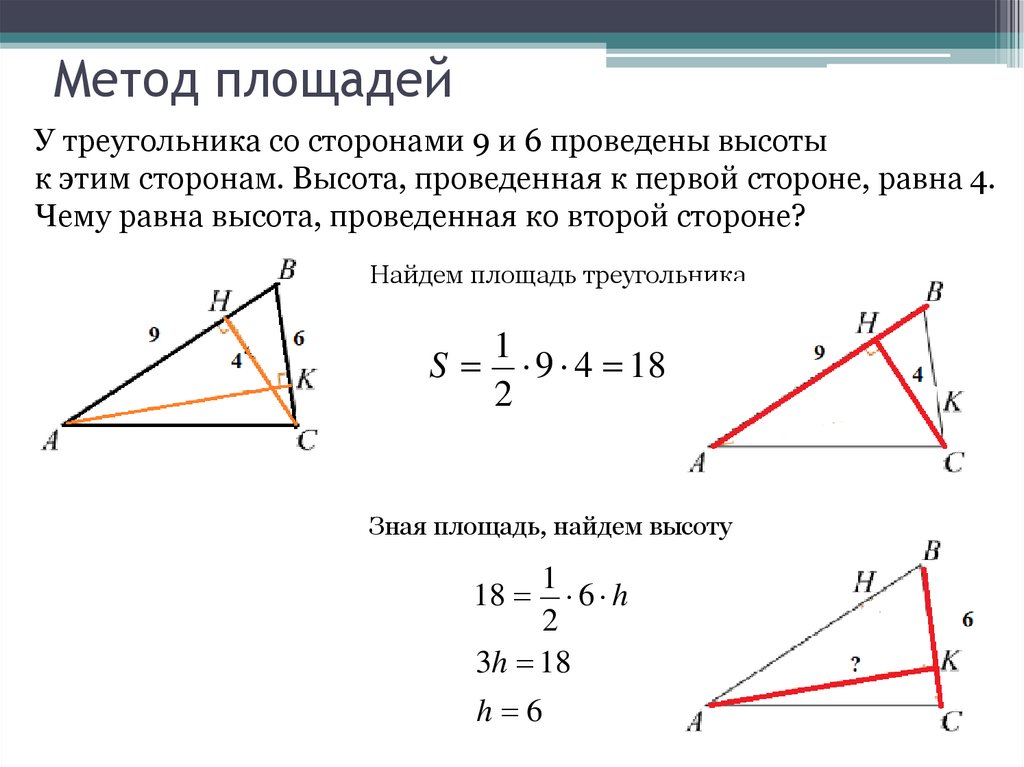
Метод площадей
У треугольника со сторонами 9 и 6 проведены высоты
к этим сторонам. Высота, проведенная к первой стороне, равна 4.
Чему равна высота, проведенная ко второй стороне?
Найдем площадь треугольника
1
S 9 4 18
2
Зная площадь, найдем высоту
1
6 h
2
3h 18
18
h 6

26.

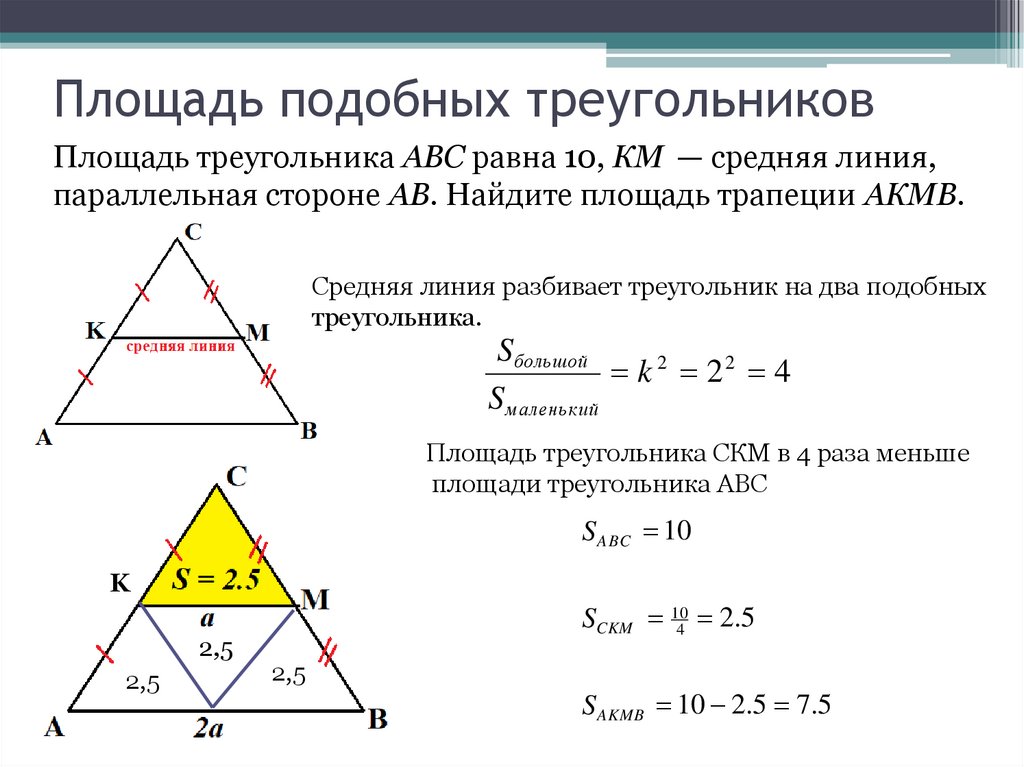
Площадь подобных треугольников
Площадь треугольника ABC равна 10, КМ — средняя линия,
параллельная стороне AB. Найдите площадь трапеции AКМВ.
Средняя линия разбивает треугольник на два подобных
треугольника.
Sбольшой
k 2 22 4
Sмаленький
Площадь треугольника СКМ в 4 раза меньше
площади треугольника АВС
S ABC 10
K
2,5
2,5
SCKM 104 2.5
2,5
S AKMB 10 2.5 7.5

27.

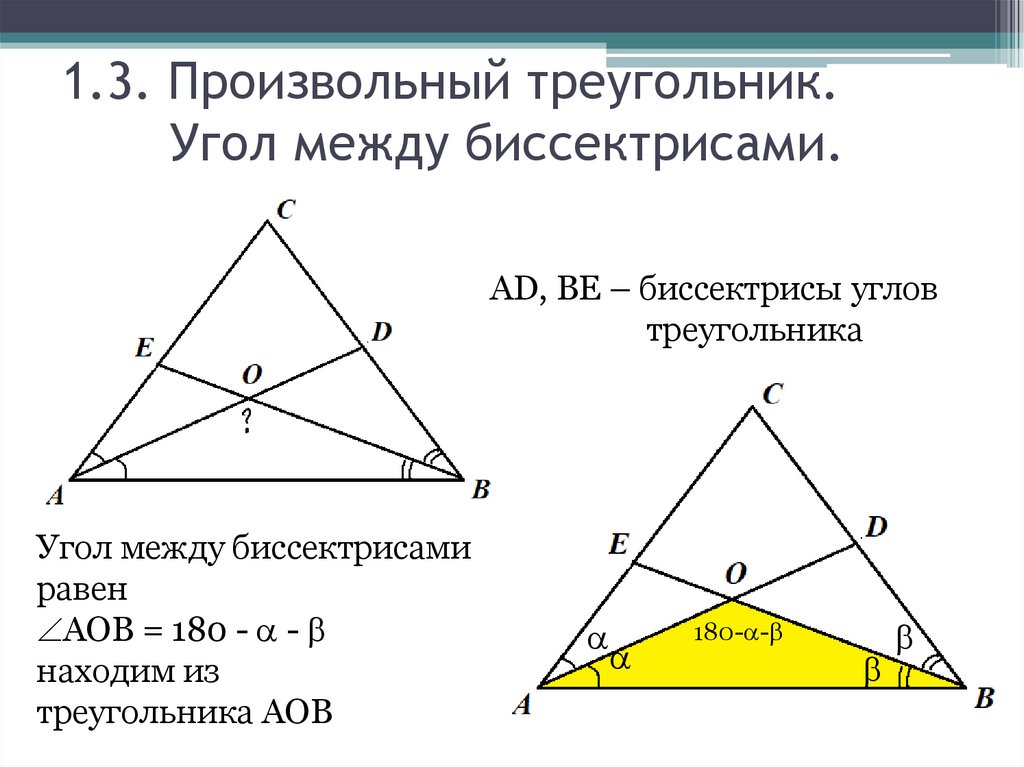
1.3. Произвольный треугольник.
Угол между биссектрисами.
AD, BE – биссектрисы углов
треугольника
Угол между биссектрисами
равен
АОВ = 180 - -
находим из
треугольника АОВ
180- -

28.

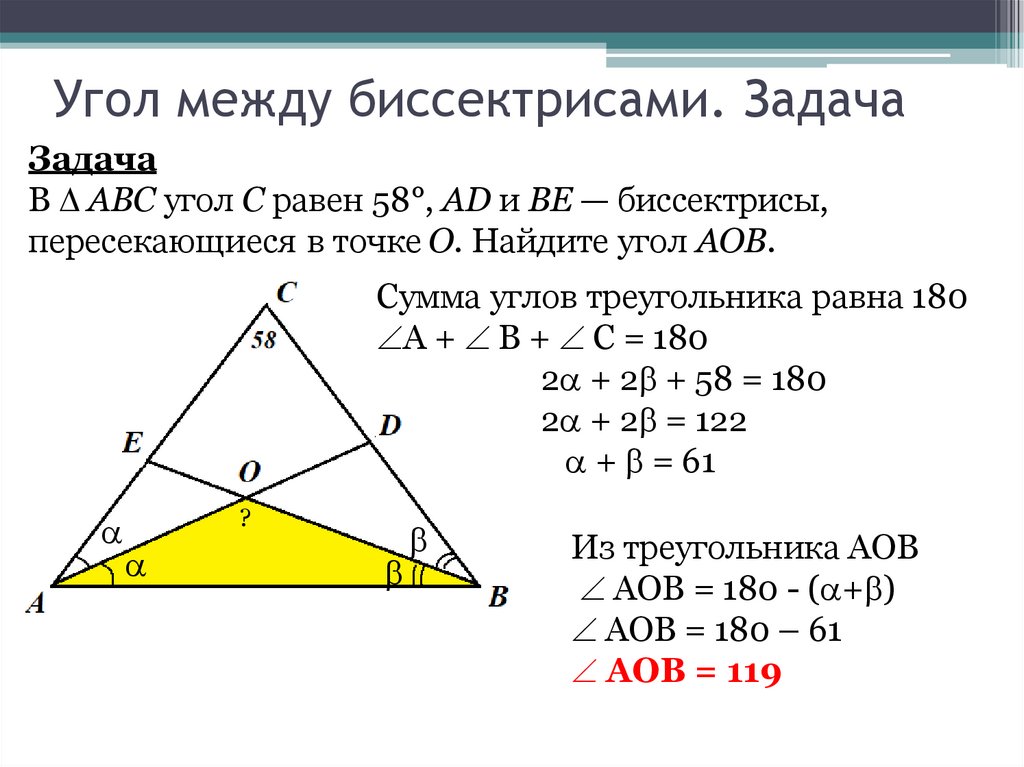
Угол между биссектрисами. Задача
Задача
В ABC угол C равен 58°, AD и BE — биссектрисы,
пересекающиеся в точке O. Найдите угол AOB.
Сумма углов треугольника равна 180
А + В + С = 180
2 + 2 + 58 = 180
2 + 2 = 122
+ = 61
?
Из треугольника АОВ
АОВ = 180 - ( + )
АОВ = 180 – 61
АОВ = 119

29.

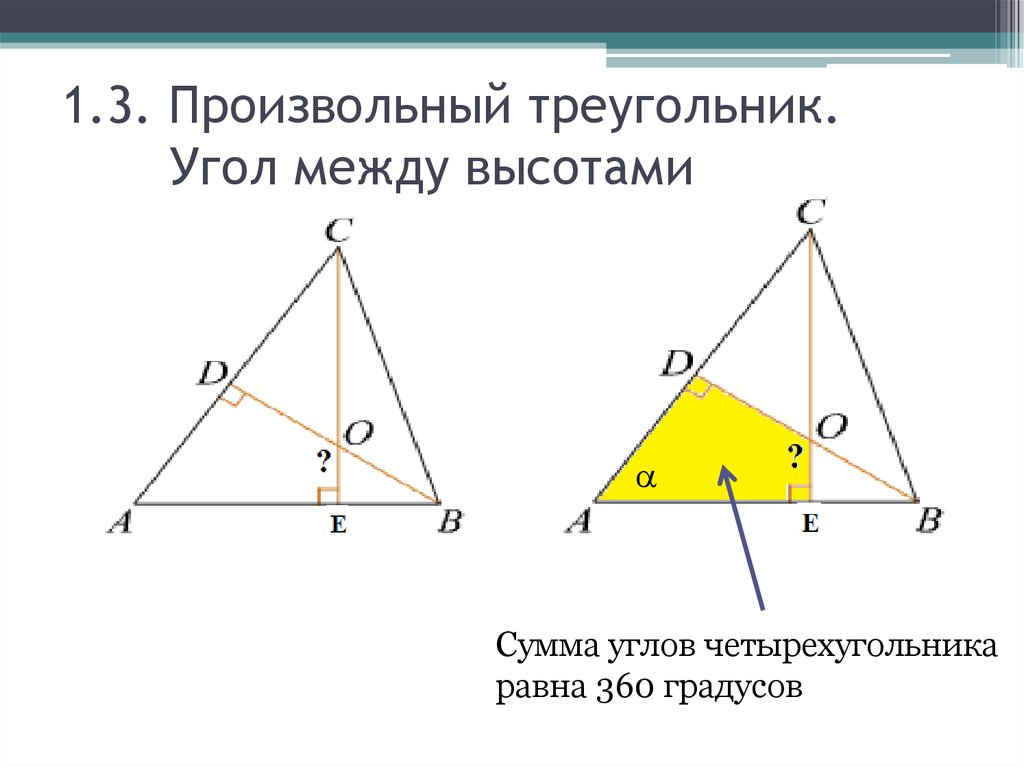
1.3. Произвольный треугольник.
Угол между высотами
Сумма углов четырехугольника
равна 360 градусов

30.

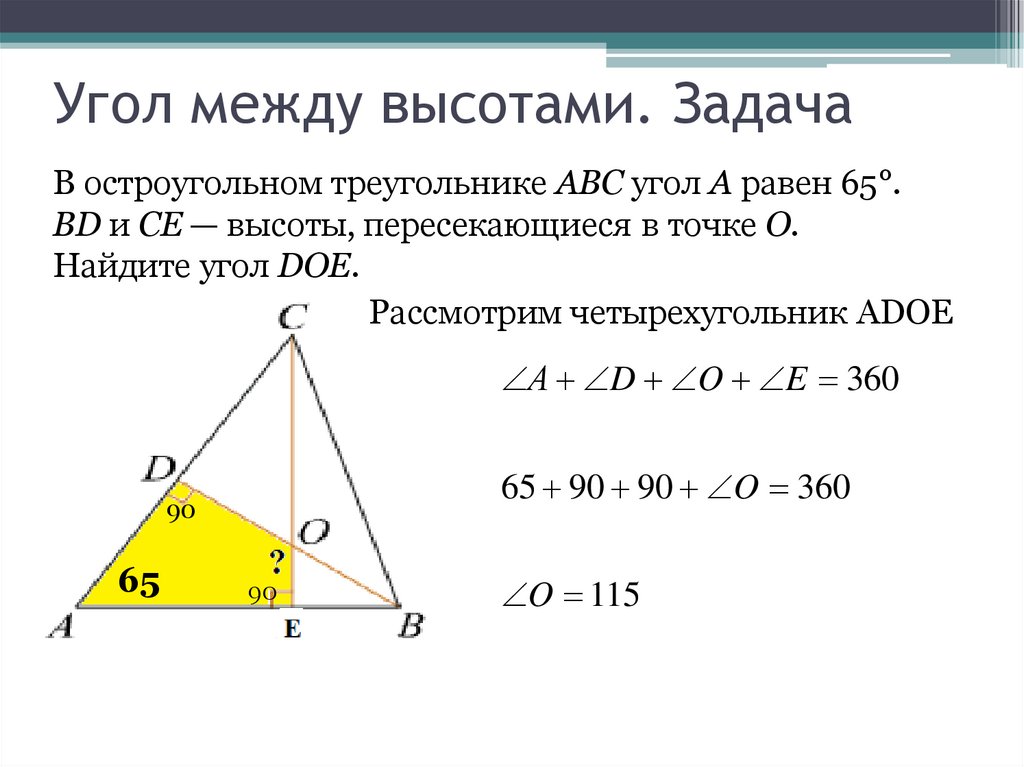
Угол между высотами. Задача
В остроугольном треугольнике ABC угол A равен 65°.
BD и CE — высоты, пересекающиеся в точке O.
Найдите угол DOE.
Рассмотрим четырехугольник ADOE
А D O E 360
65 90 90 O 360
90
65
90
O 115

31.

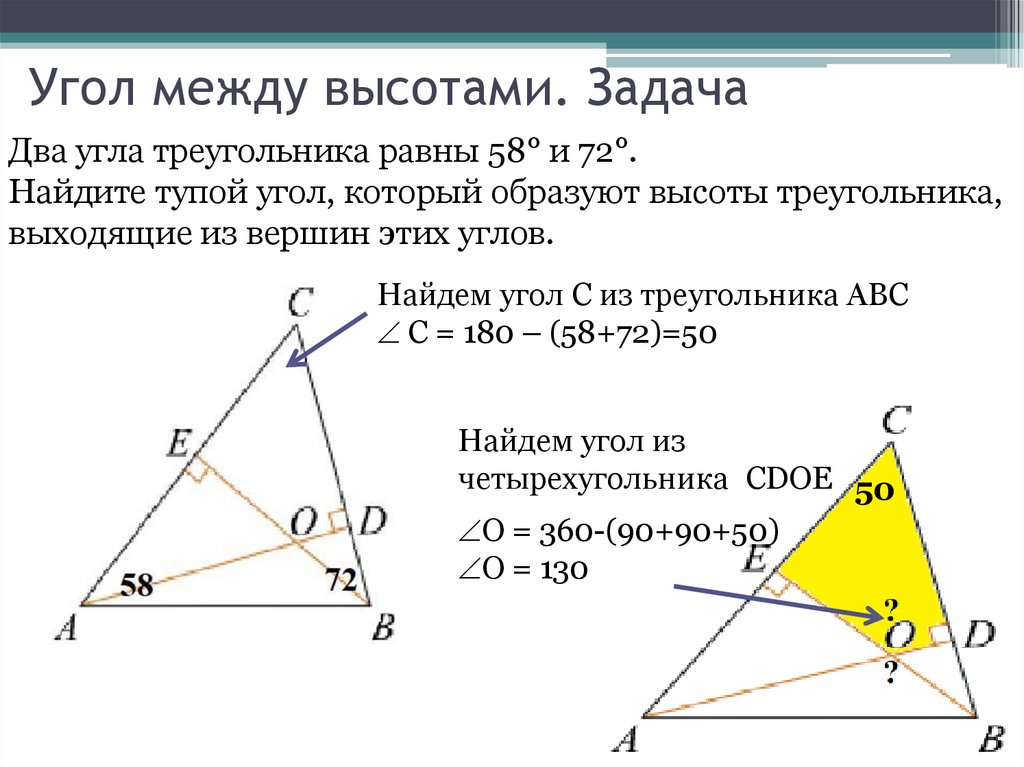
Угол между высотами. Задача
Два угла треугольника равны 58° и 72°.
Найдите тупой угол, который образуют высоты треугольника,
выходящие из вершин этих углов.
Найдем угол С из треугольника АВС
С = 180 – (58+72)=50
Найдем угол из
четырехугольника CDOE 50
O = 360-(90+90+50)
O = 130