Similar presentations:
Лекции № 5-6
1.
Числовыехарактеристики
случайных величин
2.
Характеристики, назначение которых выразитьв сжатой форме наиболее существенные особенности
распределения случайной величины, называются
числовыми характерис тиками случайной величины.
3.
Математическое ожидание,мода, медиана
4.
Пусть задана дискретная случайная величина X :X
x1
x2
…
xn
P
p1
p2
…
pn
Математиче ским ожиданием дискретной
случайной величины X называется сумма произведений
всех ее возможных значений на их вероятности :
M ( X ) x1 p1 x2 p2 xn pn .
В случае счетного множества возможных значений
M ( X ) xn p n .
n 1
Ряд xn pn должен абсолютно сходиться.
n 1
5.
Математиче ским ожиданием непрерывнойслучайной величины X называется интеграл
b
M ( X ) x f ( x)dx,
a
где f ( x) плотность распределения случайной
величины X , отличная от нуля на интервале (a, b).
В общем случае,
M ( X ) x f ( x)dx.
6.
Пусть произведено N испытаний, в которых случайнаявеличина X приняла m1 раз значение x1 , m2 раз значение x2 ,
, mn раз значение xn , где m1 m2 mn N . Среднее
арифметическое X случайной величины в результате N
опытов равно
mn
1
m1
m2
X (m1 x1 m2 x2 mn xn ) x1
x2
xn
N
N
N
N
x1w1 x2 w2 xn wn ,
где wk относительная частота (k 1, n).
При больших N : wk pk X M ( X ).
Таким образом, математиче ское ожидание
приближенн о равно среднему арифметиче скому
наблюдаемых значений случайной величины.
7.
Суммой ( разностью или произведен ием) случайныхвеличин X и Y называется случайная величина, которая
принимает все возможные значения вида xi y j ( xi y j
или xi y j ), где xi , y j возможные значения величин X и Y ,
соответственно, с вероятностями pij того, что
случайная величина X примет значение xi , а Y значение
yj :
pij P( X xi , Y y j ).
Если случайные величины X и Y независимы, то по
теореме умножения вероятностей для независимых
событий
pij P( X xi ) P(Y y j ).
8.
Рассмотрим свойства математического ожидания.1. Математическое ожидание постоянной величины
равно самой постоянной
M (C ) C.
2. Постоянный множитель можно выносить за знак
математического ожидания
M (CX ) C M ( X ).
3. Математическое ожидание суммы случайных величин
равно сумме их математических ожиданий
M ( X Y ) M ( X ) M (Y ).
9.
4. Математическое ожидание произведения независимы хслучайных величин равно произведению их математических
ожиданий
M ( X Y ) M ( X ) M (Y ).
5. Математическое ожидание отклонения случайной
величины от ее математического ожидания равно нулю :
M [ X M ( X )] 0.
10.
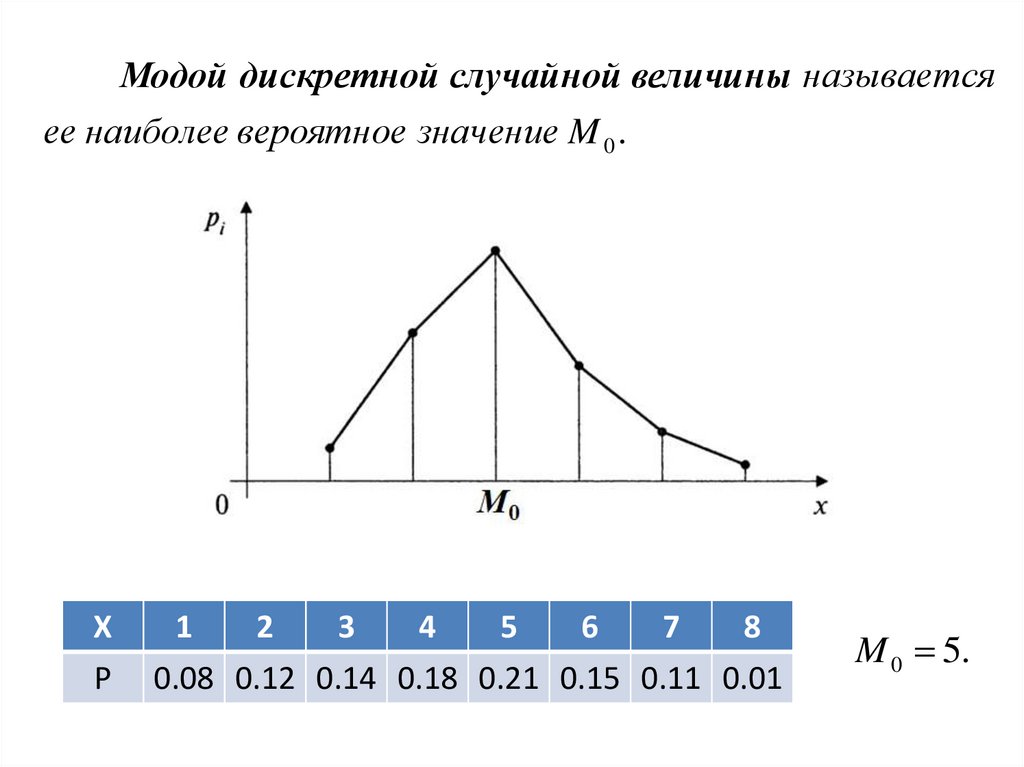
Модой дискретной случайной величины называетсяее наиболее вероятное значение M 0 .
X
P
1
2
3
4
5
6
7
8
0.08 0.12 0.14 0.18 0.21 0.15 0.11 0.01
M 0 5.
11.
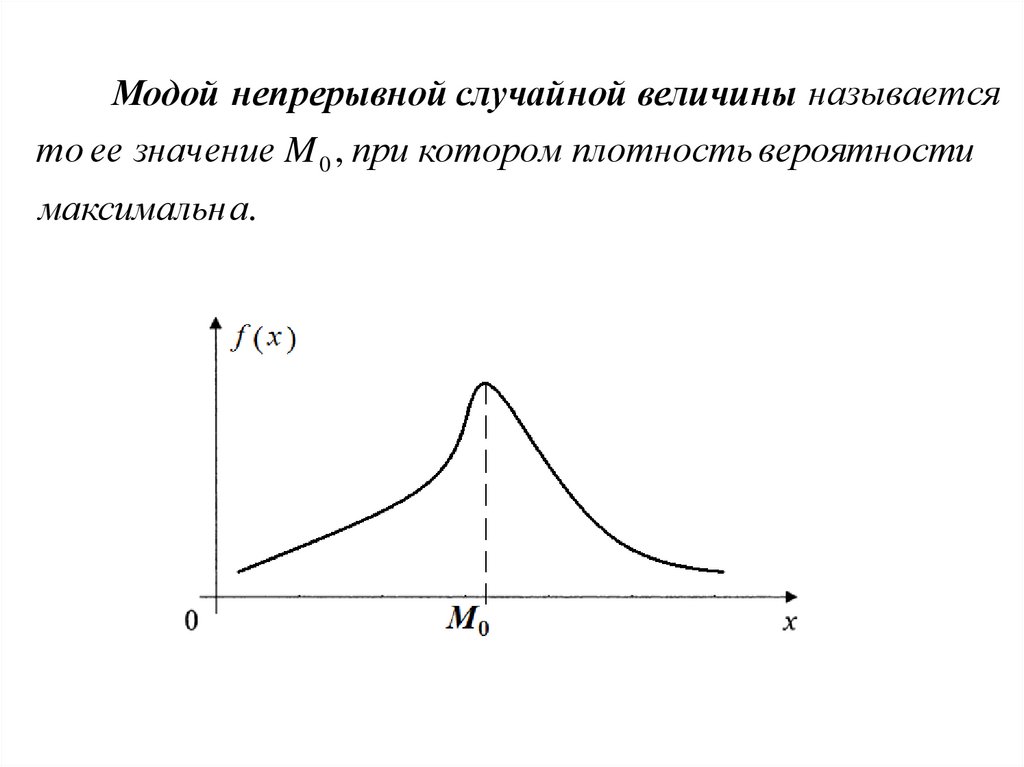
Модой непрерывной случайной величины называетсято ее значение M 0 , при котором плотность вероятности
максимальн а.
12.
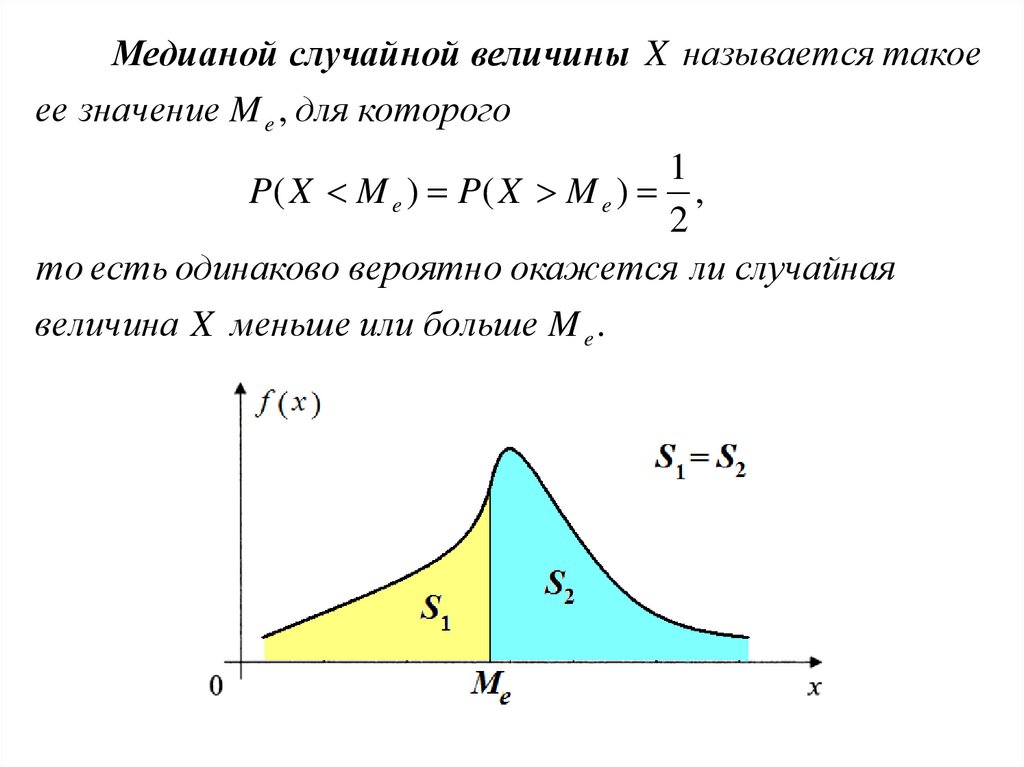
Медианой случайной величины X называется такоеее значение M e , для которого
1
P( X M e ) P( X M e ) ,
2
то есть одинаково вероятно окажется ли случайная
величина X меньше или больше M e .
13.
Моменты случайныхвеличин. Дисперсия.
Среднее квадратическое
отклонение
14.
Начальным моментом порядка k случайнойвеличины X называют математическое ожидание
случайной величины X k :
k M ( X k ),
k 1,2,
Отклонением называют разность между
случайной величиной и ее математическим ожиданием:
X M ( X ).
Центральным моментом порядка k случайной
величины X называют математическое ожидание
величины ( X M ( X )) k :
k M [( X M ( X )) k ],
k 1,2,
Заметим, что 1 M ( X ), 1 ( X ) M ( X M ( X )) 0.
15.
Если распределение случайной величины симметричноотносительно математического ожидания, то все k
нечетного порядка равны нулю и могут служить мерой
симметрии распределения относительно M ( X ).
Четные k характеризуют меру " крутости", то есть
остро или плосковершинности распределения.
Рассмотрим подробнее центральный момент 2 го
порядка называемый дисперсией случайной величины.
16.
Дисперсией случайной величины X называютматематическое ожидание квадрата отклонения
случайной величины от ее математического ожидания:
D( X ) M [( X M ( X )) 2 ].
Если X дискретная случайная величина с законом
распределения :
X
x1
x2
…
xn
P
p1
p2
…
pn
то ее дисперсия определяется по формуле :
n
D( X ) ( xi M ( X )) 2 pi .
i 1
17.
Если X непрерывная случайная величина сплотностью распределения f ( x), то
D( X ) ( x M ( X )) 2 f ( x)dx.
Рассмотрим свойства дисперсии.
1. Дисперсия случайной величины X равна разности
между математическим ожиданием квадрата
случайной величины X и квадратом ее математического
ожидания:
D( X ) M ( X 2 ) M 2 ( X ).
18.
2. Дисперсия постоянной величины равна нулюD(C ) 0.
3. Постоянный множитель можно выносить за знак
дисперсии, возведя его в квадрат
D(CX ) C 2 D( X ).
4. Дисперсия суммы независимых случайных величин
равна сумме их дисперсий
D( X Y ) D( X ) D(Y ).
19.
Средним квадратическим отклонением случайнойвеличины X называют квадратный корень из дисперсии :
( X ) D ( X ) .
Теорема.Среднее квадратическое отклонение суммы
конечного числа взаимно независимых случайных величин
равно корню квадратному из суммы квадратов средних
квадратических отклонений этих величин :
( X 1 X 2 X n ) 2 ( X 1 ) 2 ( X 2 ) 2 ( X n ) .
20.
Доказательство. Из свойства 4 дисперсии имеем :D( X 1 X 2 X n ) D( X 1 ) D( X 2 ) D( X n )
2 ( X 1 X 2 X n ) 2 ( X 1 ) 2 ( X 2 ) 2 ( X n ).
Тогда извлекая корень квадратный получаем
( X 1 X 2 X n ) 2 ( X 1 ) 2 ( X 2 ) 2 ( X n ) .
21.
Пример. Непрерывная случайная величина X заданаплотностью распределения
A sin x, x [0, ],
f ( x)
0, x [0, ].
Найти : а ) A; б ) P (0 X 3); в ) F ( x); г ) M ( X ); д) D( X ).
0
0
а ) f ( x)dx 1 f ( x)dx f ( x)dx f ( x)dx 1
0
0
0
0dx A sin xdx 0dx 1 A sin xdx 1
1
A ( cos x) 0 1 A 2 1 A .
2
22.
б ) Подставляя значение A в f ( x) , будем иметь1
sin x, x [0, ],
f ( x) 2
0, x [0, ].
Тогда
3
3
1
P(0 X 3) f ( x)dx sin xdx
0
0 2
3
1
1 1 1
( cos x) .
2
4 2 4
0
23.
xв ) Из равенства F ( x) f (t )dt находим F ( x).
x
Для x 0 : F ( x) 0dx 0;
0
x
1
1
Для 0 x : F ( x) 0dx sin xdx (1 cos x);
2
0 2
0
x
1
Для x : F ( x) 0dx sin xdx 0dx 1.
0 2
Таким образом,
0,
x 0,
1
F ( x) (1 cos x), 0 x ,
2
1,
x .
24.
г ) Из равенства M ( X ) x f ( x)dx находимматематическое ожидание M ( X ) :
1
1
M ( X ) x sin xdx xd ( cos x)
20
20
1
1
x cos x 0 ( cos x)dx sin x 0 .
2
2
0
2
То есть, M ( X ) .
2
д) Из равенства D( X ) ( x M ( X )) 2 f ( x)dx находим
дисперсию D( X ) :
25.
11
D( X ) x sin xdx x d ( cos x)
2 0
2
2 0
2
2
2
2
1
x ( cos x) 2 x ( cos x)dx
2
2
2
0
0
2
1 2 2
2 x cos xdx x cos xdx
2 4 4
2
2
0
4 0
x d (sin x) x sin x sin xdx
4 0
2
4
2
0
0
2
2
2
2
2 8
cos x 0 2
.
4
4
4
2 8
То есть, D( X )
.
4
26.
Функции случайныхаргументов
27.
Если каждому возможному значению случайнойвеличины X по некоторому закону соответствует
одно возможное значение случайной величины Y , то
Y называют функцией случайного аргумента X , и
обозначают
Y ( X ).
При составлении распределения функций по
заданному распределению аргумента X пользуются
следующими правилами.
28.
1. X дискретная случайная величина :X
x1
x2
…
xn
P
p1
p2
…
pn
а) Для функции Y ( X ) возможные значения Y
находят из равенства yi ( xi ).
б ) Если различным возможным значениям X
соответствуют различные возможные значения Y ,
то вероятности
P(Y yi ) P( X xi ), yi ( xi ).
в ) Если среди Y есть значения, равные между
собой , то их вероятности следует складывать.
29.
Пример. Дискретная случайная величина X заданараспределением
X
P
2
3
0,6 0,4
Найти распределение функции Y X 2 1.
Найдем возможные значения Y : y1 22 1 5,
y2 32 1 10. Тогда функция Y имеет распределение
Y 5 10
P 0,6 0,4
30.
Пример. Дискретная случайная величина X заданараспределением
X
P
2 1 0
1
2
0,1 0,2 0,3 0,3 0,1
Найти распределение функции Y X 2 1.
Найдем возможные значения Y : y1 ( 2) 2 1 5,
y2 ( 1) 2 1 2, y3 02 1, y4 12 1 2, y5 22 1 5.
Тогда функция Y имеет распределение
Y 1
2
5
P 0,3 0,5 0,2
31.
2. X непрерывная случайная величина с заданнойплотностью распределения f ( x).
а) Если y ( x) дифференцируемая, монотонная
функция, имеющая обратную функцию x ( y ), то
плотность распределения g ( y ) случайной величины Y
определяется по формуле
g ( y ) f [ ( y )] ( y ) .
(1)
32.
б ) Если в интервале возможных значений Xфункция y ( x) не монотонна , то этот интервал
разбивается на интервалы, где ( x) монотонна и
n
g ( y ) g i ( y ),
i 1
где g i ( y ) ищется по формуле (1) на i ом интервале
монотоннос ти функции ( x).
33.
Пример. Непрерывная случайная величина X заданаплотностью распределения
2
, x (0, 2),
f ( x)
0, x (0, 2).
Найти плотность распределения случайной величины
Y sin X .
Функция y sin x на интервале (0, 2) монотонна
и дифференцируема, и имеет обратную функцию
x arcsin y. Таким образом,
1
( y ) arcsin y, ( y )
2
1 y
34.
21
g ( y)
при y (0,1) и
2
1 y
1
g ( y) 0
0 при y (0,1).
2
1 y
Следовательно, случайная величина Y имеет плотность
распределения
2
, y (0,1),
2
g ( y) 1 y
0,
y (0,1).
35.
Рассмотрим как определяются математическоеожидание и дисперсия для функций случайных аргуметов.
1. X дискретная случайная величина с законом
распределения :
xn
X
x1
x2
P
p1
p 2 pn
Y ( X ) функция случайного аргумента. Тогда
n
M (Y ) ( xi ) pi ,
i 1
D(Y ) ( xi ) M (Y ) pi .
n
i 1
2
36.
Либо сперва составляется ряд :Y
P
y1
g1
y2 ym
g2 gm
и после математическое ожидание M (Y ) и дисперсия
D(Y ) вычисляются по формулам :
m
M (Y ) yi g i ,
i 1
D(Y ) yi M (Y ) g i .
m
i 1
2
37.
Пример. Дискретная случайная величина X заданараспределением
X
2
1
P
0,1 0,2 0,3 0,3 0,1
0
1
2
Найти M (Y ) и D(Y ) для функции Y X 2 1.
Случайная величина Y имеет распределение
Y
1
2
5
P 0,3 0,5 0,2
Тогда
M (Y ) 1 0,3 2 0,5 5 0,2 2,3,
D(Y ) (1 2,3) 2 0,3 (2 2,3) 2 0,5 (5 2,3) 2 0,2 2,01.
38.
2. X непрерывная случайная величина с заданнойплотностью распределения f ( x). Математическое
ожидание и дисперсию для функции Y ( x) случайного
аргумента можно найти по формулам :
M (Y ) ( x) f ( x)dx , D(Y ) [ ( x) M (Y )]2 f ( x)dx
или
M (Y ) yg ( y )dy , D(Y ) [ y M (Y )] g ( y )dy.
2
39.
Пример. Непрерывная случайная величина X заданаплотностью распределения
2
, x (0, 2),
f ( x)
0, x (0, 2).
Найти M (Y ) случайной величины Y sin X .
Случайная величина Y имеет плотность распределения
2
, y (0,1),
2
g ( y) 1 y
0,
y (0,1).
Тогда
1
21
1
1 1 d (1 y 2 )
2
2
2
M (Y ) y
dy
1 y .
2
2
0
0 1 y
0 1 y
40.
Пример. Непрерывная случайная величина X заданаплотностью распределения
sin x, x (0, 2),
f ( x)
0, x (0, 2).
Найти M (Y ) случайной величины Y X 2 .
Воспользуемся первой формулой из пункта 2 :
2
2
2
M (Y ) x sin xdx x d ( cos x) x ( cos x) 0
2
0
2
2
0
2
2
2
0
0
0
( cos x)2 xdx 2 x cos xdx 2 xd (sin x)
2
2
2
2 x sin x 0 sin xdx 2 cos x 0 2.
0
2





















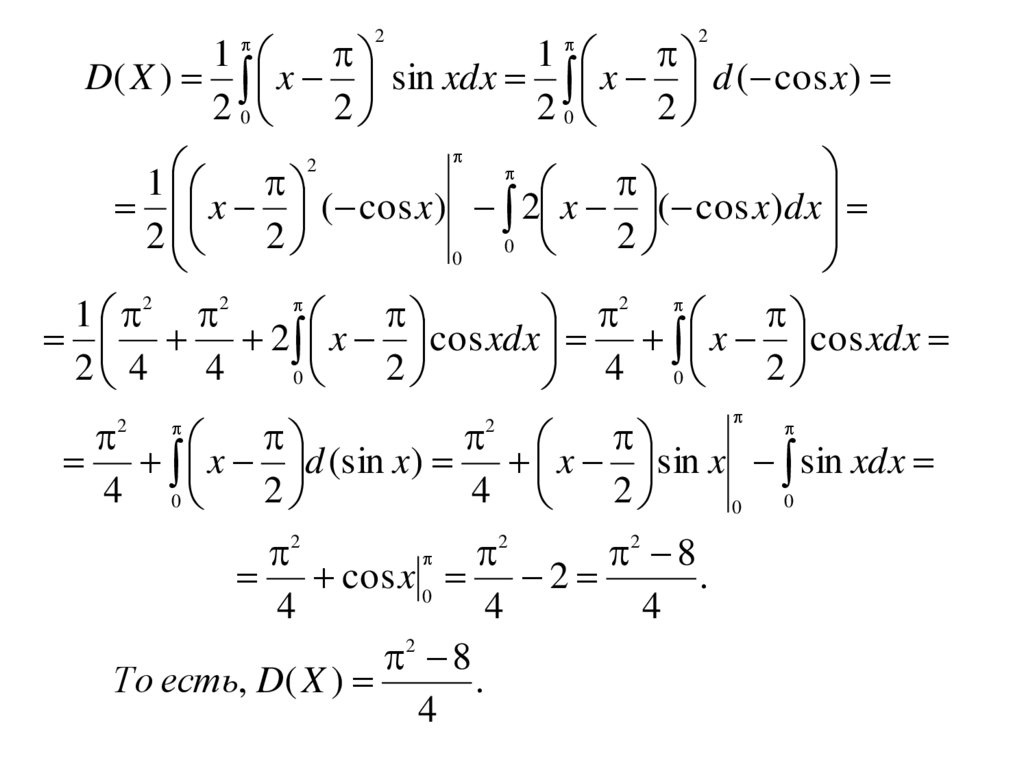
















 mathematics
mathematics








