3.40M

Category: $mathematics$ mathematics

Основы теории вероятностей и математической статистики

1.

тема № 7
ЛЕКЦИЯ
№1
Основы
теории вероятностей
и математической
статистики
Основы
теории вероятностей
Вопросы лекции:
1. Случайные события
2. Случайные величины

Вечные истины
Математику многие любят
за ее вечные истины:
дважды два всегда четыре,
сумма четных чисел четна,
а площадь прямоугольника
равна произведению его
В любой задаче,
смежных сторон.
которую мы решаем на
уроках математики, у
всех получается один и
тот же ответ – нужно
только не делать
ошибок в решении.

3.

Случайные события
Реальная жизнь оказывается не
такой простой и однозначной.
Исходы многих явлений
невозможно предсказать
заранее, какой бы полной
информацией мы о них не
располагали.
Нельзя, например, сказать
наверняка, какой стороной
упадет брошенная вверх
монета, когда в следующем
году выпадет первый снег.

4.

Случай имеет свои законы !
Однако случай тоже имеет свои законы, которые
начинают проявляться при многократном
повторении случайных явлений.
Именно такие закономерности
изучаются в специальном
разделе математики

5.

Теория вероятностей
и математическая статистика
изучает ???
«Теория вероятностей есть в сущности
не что иное, как здравый смысл,
сведенной к исчислению»
Лаплас

6.

В настоящее время Теория вероятностей
имеет статус точной науки наравне
с арифметикой, алгеброй, геометрией,
тригонометрией и т.д.
А начиналось все весьма своеобразно…

7.

Предыстория теории
вероятностей
Богатый материал для
наблюдения за
случайностью на
протяжении многих
веков давали
азартные игры.

8.

У истоков науки
В археологических
Самый древний
раскопках специально
игральный кубик
обработанные для игры найден в Северном
кости животных
Ираке и относится к IV
встречаются, начиная тысячелетию
до н.э.
с V века до н.э.

9.

• Теория вероятностей — раздел математики,
изучающий вероятности событий. Теория вероятностей
разрабатывает методы, с помощью которых можно
вычислить вероятности одних событий, зная
вероятности других. Теория вероятностей изучает также
случайные величины и их распределения.
• Испытание — опыт, действие в результате которого
наступает событие.
• Элементарное событие — простейшее событие,
которое наступает в результате случайного опыта.
Элементарное событие нельзя разложить на более
простые.

10.

Определить испытание
и случайное событие
испытание
событие
При бросании монеты
выпадает герб или цифра

11.

Виды событий
достоверные
невозможные
(обозначение: U)
(обозначение: V)
случайные
(обозначение: А, В, С и т.д.)

12.

Невозможные – те, которые в данных
условиях произойти не могут.
Пример: вода замерзла при t=+20º
Достоверные – те, которые в данных условиях
обязательно произойдут.
Пример: после зимы придет весна.
Случайные – те, которые в данных условиях
могут произойти, а могут и не произойти.
Пример: завтра утром пойдет дождь.

13.

Случайные события
• Пример: светит солнце • Пример: прилетел
инопланетянин

14.

Упражнения
• определите вид события:
1) Любому курсанту 2 курса больше
шестнадцати лет.
2) В сборнике задач по высшей математике
страница двадцать пять начинается со слова
на букву ы.
3) В группе два курсанта отмечают день
рождения 30 марта.

15.

Упражнения
• Составьте пример события по картинке
и определите его вид:
Зенит обыграет Спартак
Лиса живет в норе
Крокодил солнце проглотил

16.

Виды случайных событий
простые
сложные
совместные
несовместные
противоположные
полная группа событий
равновозможные
А

17.

Простые событие – это
элементарный исход в результате
испытания
Сложные события – события,
состоящие из нескольких
элементарных исходов

18.

События бывают:
совместные и несовместные
• Совместные – это
события, которые в
данных условиях
могут происходить
одновременно.
Пример: Наступило
лето. Стоит жаркая
погода.
• Несовместные –это
события, которые в
данных условиях не
могут происходить
одновременно.
Пример: Наступило
утро. Наступила ночь.

19.

Упражнения
• определите, события совместные или
несовместные:
1) Выпал снег. Начались соревнования по лыжам.
2) Наступил ноябрь. В летнем саду зацвела
сирень.

20.

События равновозможные
Равновозможные –это те события, которые в данных
условиях одинаково возможны.
Пример: при подбрасывании монеты возможно:
1. выпадение орла
2. выпадение решки

21.

Упражнения
• определите, являются ли события
равновозможными:
1)При подбрасывании кубика:
выпадает число 4
выпадает число 6
2)При подбрасывании кубика:
выпадает число 2
выпадает число 7

22.

Противоположным к событию А
называют событие А ,
которое происходит,
когда не происходит А

23.

Полная группа событий,
если в результате испытания
непременно произойдет хотя бы
одно из них
Полная группа попарно несовместных
событий, если в результате
испытания непременно произойдет
одно и только одно событие

24.

2)
Являются
ли событий
несовместными
события А1 и
1)Найти
среди
Аi
Адостоверные
и невозможные:
2:
испытание
- бросание
монеты;
А1 – «появление
10 очков
при бросании
события: А1 –« появление
герба»,
игральной
кости»;
А2 – «появление
цифры»;
А2 – «появление
10 очков при
бросании
испытание - бросание
игральной
кости;
трех игральных
костей»;
события:
А1 – «появление
очков»,
А3 – «появление
20 очков трех
при бросании
А2– «появление
нечетного костей»;
числа очков»;
трех игральных
испытание
- бросание
двух
монет;
А4 – «наугад
выбранное
двухзначное
число
события: А1 – «появление
на одной
негерба
больше
100»; из
монет»,
А5 – «появление двух гербов при бросании
А2 – «появление герба на двух
второй
монете »?
монет».

25.

3) Являются
4)
Образуют ли равновозможными
полную группу события:
события
испытание
А
– бросание монеты;
1 и А 2:
события: А1– –бросание
испытание
«появление
игральной
герба», кости;
события: А12 ––«появление
«появление цифры»;
двух очков»,
испытаниеА2три
– «появление
выстрела попяти
мишени;
очков»;
события: А1 бросание
испытание–«ни одного
игральной
попадания»,
кости;
события: А12 – «появление
«одно попадание»,
двух очков»,
А2 – «появление
А3 – «два попадания»,
четного числа очков»;
испытание
А4––два
«три
выстрела
попадания».
по мишени;
ЯвляютсяАли
события:
«промах
попарно
при несовместными?
первом выстреле»,
1 – они
А2 – «промах при втором выстреле»?

26.

Классическое определение вероятности
Рассмотрим группу попарно
несовместимых событий А1, А2, …, Аn,
связанную с некоторым испытанием
Событие А называется благоприятствующим
данному событию В,
если наступление события А влечет за собой
наступление события В

27.

Пусть
при
бросании
игральной
кости
Под вероятностью случайного события
события А2, А4, А6 - появление
соответственно
2,
4
и
6
очков.
понимают численную меру
А
–
событие,
состоящее
в
появлении
объективной возможности появления
четного числа очков; данного события
события А2, А4, А6 благоприятствуют
событию А

28.

Классическое
определение
вероятности
Свойства
вероятности
1.Вероятность
достоверного
события
0 PPAA m1 P A m n 1
равна единице
n
n n
2. Вероятность
невозможного
события
Вычислить
вероятность
выпадения
герба
0
m
P
A
0
равна
нулю
при одном бросании монеты
n n
3. Вероятность случайного события
есть положительное число, заключенное
между нулем и единицей 0 m n
0 P A 1
0 m
1
n

29.

СТАТИСТИЧЕСКОЕ
ОПРЕДЕЛЕНИЕ
ВЕРОЯТНОСТИ

30.

ПРОБЛЕМНЫЙ ВОПРОС 1:
А можно ли вычислить
вероятность события с
помощью ряда
экспериментов?

31.

Опыт человечества
Вероятность попасть под дождь
в Лондоне гораздо выше, чем в пустыне Сахара.
Весь наш жизненный опыт подсказывает,
что любое событие считается тем более
вероятным, чем чаще оно происходит.
Значит, вероятность должна быть какимто образом связана с частотой.

32.

Частота случайного события
Абсолютной частотой
случайного события А в серии
из N случайных опытов
называется число NA , которое
показывает, сколько раз в этой
серии произошло событие А.

33.

Частота случайного события
Относительной частотой случайного
события называют отношение числа
появлений этого события к общему
числу проведенных экспериментов:
NA
W ( A)
N
где А – случайное событие по отношению к
некоторому испытанию,
N раз проведено испытание и при этом событие А
наступило в NA случаях.

34.

Примеры
Пример 1. Наблюдения показывают, что
в среднем среди 1000 новорожденных
детей 515 мальчиков. Какова частота
рождения мальчика в такой серии
наблюдений?
515
W ( A)
0,515
1000
Ответ: 0,515

35.

Примеры
Пример 2. За лето на Черноморском
побережье было 67 солнечных дней.
Какова частота солнечных дней на
побережье за лето? Частота пасмурных
дней?
67
25
W ( A)
0,728 W ( B )
0,272.
92
92
Ответ: 0,728; 0,272.

36.

Примеры
Пример 3. Отдел технического контроля
обнаружил 5 бракованных изделий в
партии из 1000 изделий. Найдите частоту
изготовления бракованных изделий.
Ответ: 0,005

37.

Примеры
Пример 4. Для выяснения качества
семян было отобрано и высеяно в
лабораторных условиях 1000 штук.
980 семян дали нормальные всходы.
Найдите частоту нормального всхода
семян.
Ответ: 0,98

38.

ПРОБЛЕМНЫЙ ВОПРОС 2:
Может быть,
относительную частоту и
нужно принять за
вероятность?

39.

Фундаментальным свойством
относительных частот является тот
факт, что с увеличением числа опытов
относительная частота случайного
события постепенно
стабилизируется и приближается к
вполне определенному числу, которое
и следует считать его
вероятностью.

40.

Проверка
Пример 5. Подбрасывание монеты.
А – выпадает герб.
Классическая вероятность:
всего 2 исхода, 1 исход события А:
1
P( A) 0,5
2

41.

Проверка
Жорж Бюффон
Пример 5. Французский
естествоиспытатель
Бюффон (XVIII в.) бросил
монету 4040 раз, и при
этом герб выпал в 2048
случаях. Следовательно,
частота выпадения герба в
данной серии испытаний
равна:
2048
W ( A)
4040
0,50693...

42.

Проверка
Карл Пирсон
Пример 5. Английский
математик Карл Пирсон
(1857-1936) бросал монету
24000 раз, причем герб
выпал 12012 раз.
Следовательно, частота
выпадения герба в данной
серии испытаний равна:
12012
W ( A)
0,5005
24000

43.

Результаты
1
P( A) 0,5
2
W ( A) 0,50693...
W ( A) 0,5005
Вывод
Пример 5 подтверждает естественное
предположение о том, что вероятность
выпадения герба при одном бросании монеты
равна 0,5.

44.

Статистическая вероятность
Вероятность случайного события
приближенно равна частоте этого
события, полученной при проведении
большого числа случайных
NA
экспериментов: P( A) , где N A - число
N
испытаний, в которых наступило
событие А, N – общее число испытаний.

45.

Задача №6.
Чтобы определить, как часто встречаются в лесопарке
деревья разных пород, ребята провели следующие
эксперименты. Каждый выбрал свою тропинку и по
пути следования записывал породу каждого десятого
дерева.
Результаты были занесены в таблицу:
Породы
Сосна Дуб Береза Ель Осина Всего
Число деревьев 315 217
123 67
35
757
Оцените вероятность того, что выбранное наугад в этом
парке дерево будет:
а) сосной;
б) хвойным;
в) лиственным.
Указание. Ответ запишите в виде десятичной дроби с
тремя знаками после запятой.

46.

Задача №6.
Решение:
а) A={выбранное наугад в парке дерево - сосна}
NА = 315, N = 757, Р(А) = 315/757 0,416;
б) В ={выбранное наугад в парке дерево - хвойное}
NА = 315 + 67 = 382, N = 757.
Р(А) = 382/757 0,505;
в) C = {выбранное наугад в парке дерево - лиственное}
NА = 217 + 123 + 35 = 375, N = 757.
Р(А) = 375/757 0,495.

47.

Задача №7.
По статистике, на каждые 1000 лампочек
приходится 3 бракованные. Какова
вероятность купить исправную
лампочку?
Решение:
3/1000 = 0,003
1 – 0,003 = 0,997

48.

Задача №8.
Демографы утверждают, что вероятность
рождения близнецов равна 0,012. В скольких
случаях из 10 000 рождений можно ожидать
появление близнецов?
Решение:
P ( A) 0,012
N 10000
NA
P ( A)
N
NA
0,012
10000
N A 0,012 10000 120
Ответ: в 120 случаях.

49.

Основные формулы
комбинаторики

50.

Что же такое «Комбинаторика»?
Комбинаторика – это раздел математики, в
котором исследуются и решаются задачи выбора
элементов
из
исходного
множества
и
расположения их в некоторой комбинации,
составленной по заданным правилам.

51.

Правила сложения и умножения
в комбинаторике
Правило суммы
Если два действия А и В взаимно исключают
друг друга, причем действие А можно
выполнить m способами, а В – n способами,
то выполнить одно любое из этих действий
(либо А, либо В) можно n + m способами.

52.

Пример
В группе учится 20 юношей и 5 девушек.
Сколькими способами можно назначить одного
дневального?
Решение
Дневальным можно назначить либо юношу,
либо девушку, т.е. дневальным может быть
любой из 20 юношей, либо любая из 5
девушек. По правилу суммы получаем, что
одного дневального можно назначить 20+5=25
способами

53.

Правило произведения
Пусть
требуется
последовательно k действий.
выполнить
Если первое действие можно выполнить n1
способами, второе действие n2 способами,
третье – n3 способами и так до k-го действия,
которое можно выполнить nk способами, то
все k действий вместе могут быть
выполнены:
N n1 n2 ... nk

54.

Пример. В группе учится 20 юношей и 5 девушек.
Сколькими
способами
можно
назначить
двух
дневальных?
Решение
Первым дневальным можно назначить либо юношу, либо
девушку. Т.к. в группе учится 20 юношей и 5 девушек, то
назначить первого дневального можно 20+5=25
способами.
После того, как мы выбрали первого дневального,
второго мы можем выбрать из оставшихся 24 человек, т.е.
24-ю способами.
По теореме умножения двое дневальных могут быть
выбраны 25*24=600 способами.

55.

Размещениями из
n различных элементов по m
m n
называют комбинации, составленные из
данных n элементов по m элементов,
которые
отличаются
либо
самими
элементами, либо порядком элементов.
m
An
n!
n ( n 1) ( n 2) ... [ n ( m 1)]
n m !
m
n ! 1 2 3 ... n

56.

Пример. Сколько можно составить сигналов из 6 флажков различного
цвета, взятых по 2?
Искомое число сигналов
2
A6
6!
4!
1 2 3 4 5 6
1 2 3 4
5 6 30 .

57.

Пример. Группа слушателей второго курса изучает 10
различных дисциплин. Сколькими способами можно
составить расписание занятий в среду, если в этот день
должно быть три пары по различным дисциплинам?
Способов составления расписания из 10 дисциплин по
три существует столько, сколько можно составить
размещений из десяти предметов по три, так как способы
могут отличаться друг от друга как порядком (первая пара
по дисциплине «Высшая математика» или по дисциплине
«Физика» – это разница), так и хотя бы одной
дисциплиной:

58.

Перестановками из n различных элементов
называют размещения из этих n по n
Pn n n 1 n 2 ... 3 2 1 n !

59.

Пример.
Для лечения заболевания применяют три лекарства.
Полагают, что последовательность, в которой принимают
лекарства, оказывает существенное влияние на результаты
лечения.
Сколько имеется различных порядков назначения этих
лекарств?
P3 3! 6

60.

Сочетаниями из
n различных элементов по m
m n
называют комбинации, составленные из
данных n элементов по m элементов,
которые отличаются хотя бы одним
элементом.
m
Cn
m
An
Pm
n n 1 n 2 ... n m 1
1 2 3 ... m 1 m
n!
m !( n m )!

61.

Пример. Сколько существует способов выбрать два
цветка из корзины, в которой 5 роз и 4 хризантемы?
Два цветка выбираем из девяти. В данном случае не
важно, какой цветок будет первым в паре. Количество
способов будет равно:
2
C9
9!
2! 7!
7! 8 9
1 2 7!
8 9
2
36

62.

Алгоритм выбора формулы для вычисления
количества комбинаций
Cnm
m
An n!
n m !
n!
m! n m !

63.

1.Из
трех
элементов
2, 5, 6 можно
составить
3. Для
лечения
заболевания
применяют
по два элемента следующие размещения:
три лекарства.
Полагают, что последовательность,
(2; 5), (5 ;2 ), (2; 6), (6; 2), (5; 6), (6; 5)
в которой принимают лекарства, оказывает
2.
Сколько можно
составить
сигналов из
существенное
влияние
на результаты
6 флажков различного цвета, взятых по 2?
лечения.
2
6!
Сколько
порядков
A6имеется
6! различных
5
6
30
6 2!
4!
назначения этих
лекарств?
P 3! 6
3

64.

4. В корзине 3 белых и 2 черных шара.
Найти число способов выбора двух шаров,
если они могут быть любого цвета
С52
5! 5! 4 5 10
2
2! 5 2 ! 2!3!
5. Набирая номер телефона, абонент забыл
две последние цифры и, помня лишь, что эти
цифры различны, набрал их наудачу.
Какова вероятность того, что номер набран
правильно?
P A 1 1 1
2 9 10 90
A10

65.

Схема выбора с возвращением
Если при упорядоченной выборке m
элементов из n элементы возвращаются
обратно,
то
полученные
выборки
представляют собой
размещения с повторениями
m
An
n
m

66.

Пример. Сколько существует четырёхзначных пинкодов?
По условию задачи нам предложен набор из n = 10
цифр, из которого выбираются m = 4 цифры и
располагаются в определенном порядке, при этом цифры в
выборке могут повторяться (т. е. любой цифрой исходного
набора можно пользоваться произвольное количество раз).
Найдем количество пин-кодов по формуле размещений
с повторениями:
4
A10
10 10 000
4

67.

Схема выбора с возвращением
Пусть в множестве из n элементов есть m
различных типов элементов, при этом 1-й тип
повторяется n1 раз, 2-й − n2 раз, …, п-й − nm
раз, причем
n1 + n2 + … + nm = n.
Тогда перестановки элементов данного
множества
представляют
собой
перестановки с повторениями
Pn n1 , n2 ,..nm
n!
n1 ! n2 ! ... nm !

68.

Пример. Сколько существует способов расположения
шахматных фигур на первой линии шахматной доски?
Порядок важен, места на доске различны, но есть
повторения (2 ладьи, 2 слона и 2 коня).
Нужна формула перестановки с повторениями, n = 8,
n1 = 1, n2 = 1, n3 = 2, n4 = 2, n5 = 2. Их число:
P8 1,1, 2, 2, 2
8!
1!1!2!2!2!
1 2 3 4 5 6 7 8
1 1 2 2 2
5 040

69.

Схема выбора с возвращением
Если при выборке m элементов из n элементы
возвращаются обратно без последующего
упорядочивания (таким образом, одни и те же
элементы могут выниматься по нескольку раз,
т.е. повторяться), то полученные выборки есть
сочетания с повторениями
m
Cn
m
Cn m 1

70.

Задача: Сколько трехзначных чисел можно
составить из цифр 1, 2, 3, 4, 5?
Решение: Так как порядок цифр в числе
существенен, цифры могут повторяться, то
это будут размещения с повторениями из
пяти элементов по три, а их число равно:
3
5
А 5 125
3

71.

Задача: В кондитерском магазине продавались 4 сорта
пирожных: эклеры, песочные, наполеоны и слоеные.
Сколькими способами можно купить 7 пирожных.
Решение: Покупка не зависит от того, в каком порядке
укладывают купленные пирожные в коробку. Покупки
будут различными, если они отличаются количеством
купленных пирожных хотя бы одного сорта.
Следовательно, количество различных покупок равно
числу сочетаний четырех видов пирожных по семь -
7
C4
10! 7! 8 9 10
C
C
120
7! 1 2 3
4 7 1
10 7! 3!
7
7

72.

Задача:
Сколькими
способами
переставить буквы слова «ананас»?
можно
Решение: всего букв 6. Из них одинаковы
n1«а»=3, n2«н»=2, n3«с»=1.
Следовательно, число различных перестановок
равно
P 6 3,2,1
6!
3!2!1!
3! 4 5 6
3!1
2 1
60

73.

Операции над событиями

74.

Операции над случайными событиями
Суммой
Суммой
А+В = С
A A1 A2 ... Ak
A1, A2 ,..., Ak
Испытание – стрельба двух стрелков
(каждый делает поВодному выстрелу)
А
Событие А–попадание в мишень первым стрелком;
Событие В - попадание в мишень вторым стрелком.
Суммой событий А+В = С является событие …

75.

Операции над случайными событиями
Произведением
А В = С
Испытание – стрельба двух стрелков
A1, A2выстрелу)
,..., Ak
Произведением
(каждый
делает по одному
A A1 A2 ... Ak
Событие А – попадание в мишень
первым
стрелком,
В
А
Событие В - попадание в мишень вторым стрелком.
Произведением событий А∙В является событие …

76.

Операции над случайными событиями
Отрицанием события А
А
А
А
Испытание – стрельба одного стрелка
Событие А – попадание в мишень стрелком
Событие А - промах по мишени

77.

Теоремы сложения вероятностей
Когда наступит событие С = А + В?
А или В или они наступят вместе
несовместные
А или В
совместные
А или В или А В

78.

Теорема
Вероятность суммы двух несовместных
событий А и В равна …
P A B P A P B

79.

Теорема
Вероятность суммы конечного числа
попарно несовместных событий
A1, A2 ,..., An
равна …
P A1 A2 ... An P A1 P A2 ... P An

80.

Теорема
Вероятность суммы двух совместных
событий равна …
P A B P A P B P A B

81.

Следствие 1
A1, A2 ,..., An
полная группа
попарно несовместных событий
P A1 P A2 ... P An 1
Следствие 2
P A P A 1

82.

Пример. В коробке имеется 250 лампочек, из них 100 по 90 Вт, 50 – по 60 Вт, 50 –
по 25 Вт и 50 – по 15 Вт. Определить вероятность того, что мощность любой наугад
взятой лампочки не превысит 60 Вт.
Решение.
Рассматриваем следующие события:
А = {мощность лампочки равна 90 Вт}, вероятность Р(А)=100/250=0,4;
В = {мощность лампочки равна 60 Вт};
С = {мощность лампочки равна 25 Вт};
D = {мощность лампочки равна 15 Вт}.
События А, В, С, D образуют полную группу, так как все они несовместны и одно из
них обязательно наступит в данном опыте (выборе лампочки).
Вероятность наступления одного из них есть достоверное событие, тогда
Р(А)+Р(В)+Р(С)+Р(D)=1.
События {мощность лампочки не более 60 Вт} (т.е. меньше или равна 60 Вт), и
{мощность лампочки более 60 Вт} (в данном случае – 90 Вт) являются
противоположными.
По свойству противоположных чисел Р(В)+Р(С)+Р(D)=1-Р(А).
Учитывая, что Р(В)+Р(С)+Р(D)=Р(В+С+D), получим
Р(В+С+D)=1-Р(А)=1-0,4=0,6.

83.

Пример. Два стрелка стреляют в одну и ту же цель, причём вероятность поражения
цели первым стрелком 0,8, а вторым стрелком 0,5. Оба стрелка стреляют одновременно
и один раз. Какова вероятность того, что цель будет поражена хотя бы одним из
стрелков?
Решение:
Пусть А – попадание в цель первым стрелком,
В – вторым стрелком,
А+В – поражение цели хотя бы одним стрелком,
А·В – поражение цели обоими стрелками.
Тогда Р(А+В) = 0,8 + 0,5 – Р(А·В).
Считая события А и В независимыми имеем:
Р(А·В) = Р(А)·Р(В) = 0,8·0,5 = 0,4.
Тогда Р(А+В) = 0,8 + 0,5 – 0,4=0,9.

84.

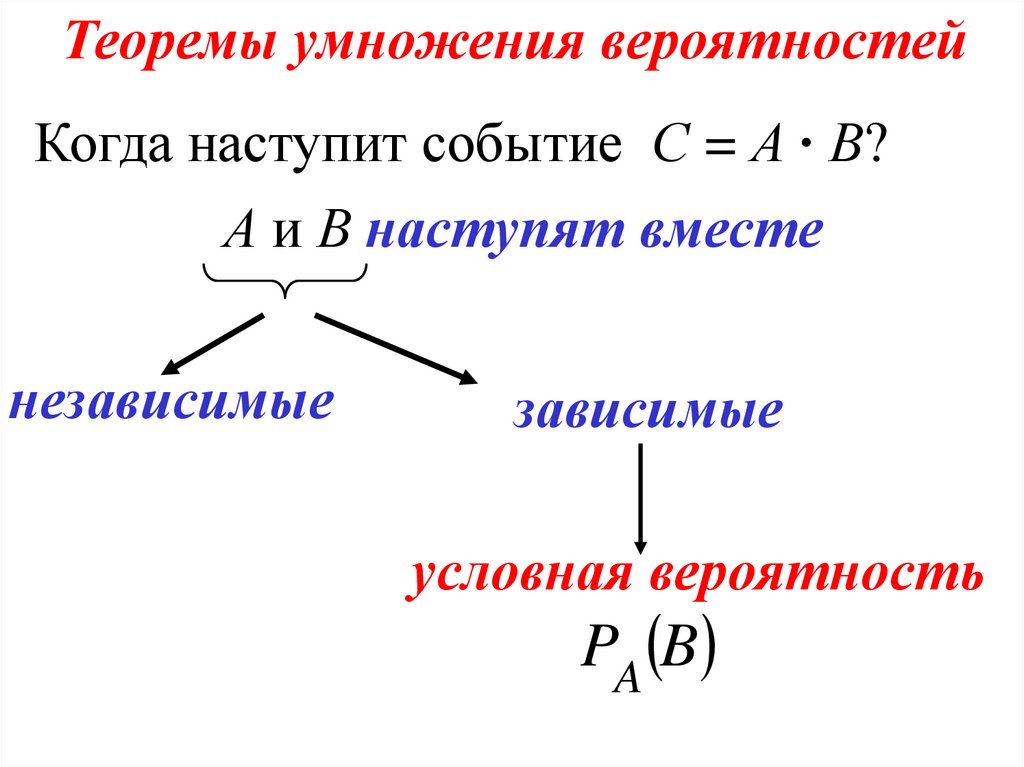
Теоремы умножения вероятностей
Когда наступит событие С = А ∙ В?
А и В наступят вместе
независимые
зависимые
условная вероятность
PA B

85.

Теорема
Вероятность произведения двух
зависимых событий А и В равна …
P A B P A PA B

86.

Теорема
Вероятность произведения двух независимых
событий равна …
P AB P A P B

87.

Пример. В ящике имеются 7 белых и 5 чёрных шаров, отличающихся
лишь цветом. Опыт состоит в том, что сначала вынимают (не глядя) один шар
и, не опуская его обратно, вынимают ещё один шар. Какова вероятность, что
оба вынутых шара чёрные?
Решение: Появление первого чёрного шара (событие А) имеет
5
вероятность P A . Если первый шар оказался чёрным, то условная
12
вероятность события В – появление второго чёрного шара (при условии, что
4
P
B
первый шар был чёрным) – равна A
, т.к. перед выниманием второго
11
шара осталось 11 шаров, из них 4 чёрных. Вероятность вынуть два чёрных
шара подряд можно подсчитать по формуле:
5 4
5
P A B P A PA B
.
12 11 33

88.

Пример. Три ящика содержат по 10 деталей. В первом ящике - 8
стандартных деталей, во втором - 7, в третьем - 9. Из каждого ящика наудачу
вынимают по одной детали. Найти вероятность того, что все три вынутые
детали окажутся стандартными.
Решение. Вероятность того, что из первого ящика взята стандартная
8 4
.
деталь (событие А), P A
10 5
Вероятность того, что из второго ящика взята стандартная деталь
7
(событие В), P В
.
10
Вероятность того, что из третьего ящика взята стандартная деталь
9
(событие С), P С . Так как события А, В и С независимые в
10
совокупности, то искомая вероятность (по теореме умножения):
4 7 9
P A B С P A P B P С
0,504
5 10 10

89.

90.

Брошены 3 игральные кости. Определить
вероятность того, что выпадет три «шестерки».

91.

Круговая мишень состоит из зон с номерами
1, 2, 3.
Вероятности попадания в эти зоны при одном
выстреле соответственно равны 0,1; 0,35 и 0,4.
Найти вероятность: попадания в первую или
третью зоны.

92.

Пусть А и В – некоторые события, связанные с
одним опытом, причем Р(А) = 0,25 и Р(В) = 0,35.
Предполагая, что А и В независимы, вычислите
вероятность того, что произошло одно из событий
А и В.

93.

Студент разыскивает нужную ему формулу в трех
справочниках. Вероятность того, что формула
содержится в 1, 2 и 3 справочнике соответственно
равна 0,6; 0,7; 0,8.
Найти вероятность того, что формула содержится
только в двух справочниках.

94.

В группе 25 студентов, из них 10 юношей и 15
девушек.
Какова вероятность того, что из вызванных наудачу
трех студентов первые две девушки, третий –
юноша?

95.

Ученик получает оценку от 2 до 5 баллов.
Вероятности того, что ему поставят «4», «3» и «2»,
соответственно равны 0,45, 0,23 и 0,09.
Определите вероятность того, что он получит
оценку не ниже «4».

96.

В группе, состоящей из 25 студентов, спортивный
разряд по борьбе имеют 10 человек, по стрельбе –
12.
Вероятность того, что студент этой группы имеет
разряды по обоим видам спорта, равна 0,32.
Найдите вероятность того, что наугад выбранный
студент имеет какой-нибудь разряд.

97.

Два стрелка произвели по одному выстрелу.
Вероятность попадания в мишень
стрелком равна 0,5, вторым 0, 7.
первым
Найти вероятность того, что хотя бы один из
стрелков попал в мишень.

98.

Формула
полной вероятности

99.

Формула полной вероятности
Теорема. Вероятность события А, которое
Pможет
P H n PH A
A Pнаступить
P Hпри
A ... появления
2 PHусловии
H1 PH1 Aлишь
2
одного из п попарно несовместных
событий n
H1,H2,...,Hn,
образующих полную группу, равна сумме
произведений вероятностей каждого из этих
событий на соответствующую условную
вероятность события А:
События H1,H2,...,Hn называются гипотезами

100.

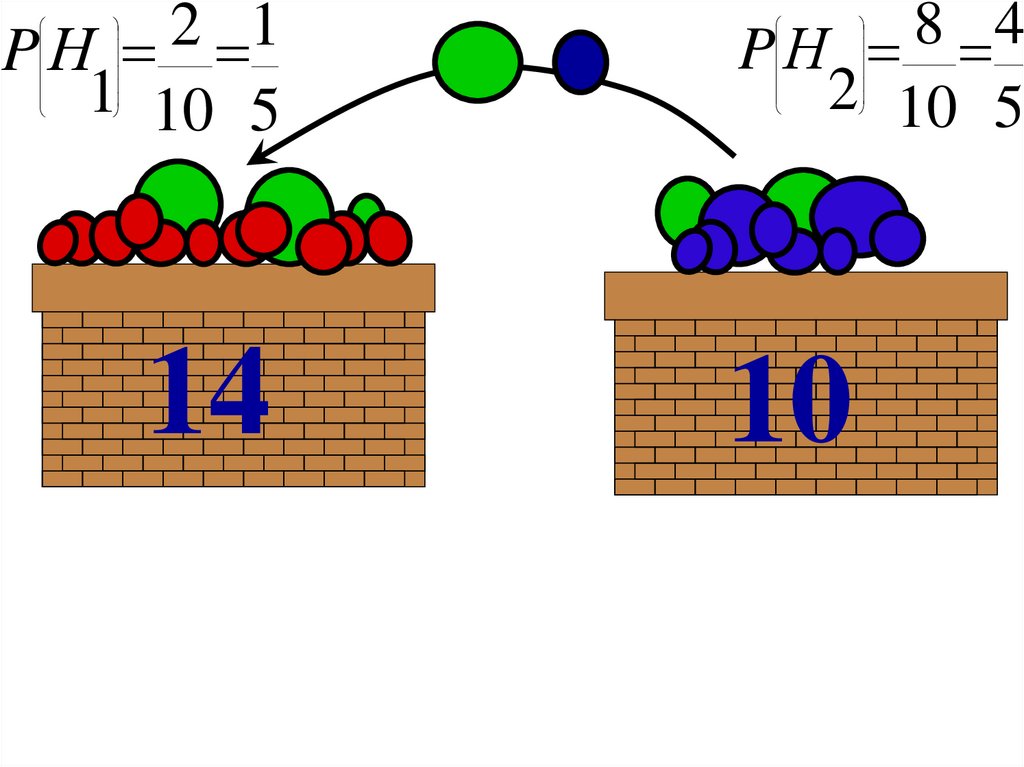
Пример. В двух корзинах имеются шары.
В первой корзине 14 шаров, из них 3 зеленого цвета. Во второй
корзине 10 шаров, из них 2 зеленого цвета.
Из второй корзины наудачу взят один шар и переложен в первую
корзину. Найти вероятность того, что взятый наудачу шар из первой
корзины окажется зеленым.

101.

?
P A ?
14
10
Н1
Н2
P A P H1 PH A P H2 PH A
1
2

102.

2
1
PН
1 10 5
14
8
4
PН
2 10 5
10

103.

15
14
10
9
4
3
1
4
1
4
1
16
PН АP A P Н А
1
15 15 5 5 52 7515 5

104.

Формула Байеса используется для переоценки
вероятностей доопытных гипотез.
Для оценки вероятности появления некоего события А выдвигают
ряд несовместных гипотез (все возможные решения), которые
могут повлечь за собой событие А.
Перед
началом
эксперимента
выдвинутым
гипотезам
приписываются предположительные вероятности.
Далее эти гипотезы можно проверить с помощью эксперимента.
Целью эксперимента является разумная коррекция этих
доопытных вероятностей.
В результате эксперимента эти доопытные вероятности заменяются
послеопытными, причем некоторые из них могут оказаться
настолько малыми, что позволяют отбросить соответствующие
гипотезы из дальнейших рассмотрений.
Опыт с оставшимися гипотезами можно повторить, каждый раз
уточняя их вероятности. Таким образом мы можем выстроить
рейтинг гипотез, выводя на первые позиции те, которые наиболее
вероятно повлекут за собой событие А.

105.

P HkФормула
PH A Байеса
k
P
H
Пусть
одно
испытание,
A kпроизведено
P
A
в результате которого произошло событие А.
А PАH
Как, в связи с тем, чтоPсобытие
уже
j PH
n
j 1
j
произошло, изменились величины P H ,
k 1,2,...,n
P Hk PH A
k
P
H
n
PA Hk ?A k P H j PH A
j 1
j
k
A

106.

Пример. Предположим, что 5% мужчин и
0,25% всех женщин имеют рост выше 180 см,
наугад выбранное лицо имеет рост
выше 180 см считая, что мужчин и женщин
одинаковое количество, найти вероятность
того, что этот человек:
а) мужчина; б) женщина.

107.

Событие А – выбранный человек оказался
ростом выше 180 см
Гипотеза H
- выбранный человек мужчина
1
Гипотеза H - выбранный человек женщина
2
P H P H 0,5
1
2

108.

P A ?
PH A 0,05
1
PH A 0,0025
2
P A 0,5 0,05 0,5 0,0025 0,02625

109.

а)
P H P A
1 H
1 0,5 0,05 20
P H
A 1
0,02625 21
PA
б)
P H P A
2 H
2 0,5 0,0025 1
P H
A 2
0,02625 21
PA

110.

Пример. Известно, что 30% приборов собирает
специалист высшей квалификации, 70% приборов –
специалист средней квалификации. Вероятность того, что
прибор, собранный специалистом высшей квалификации,
надёжен, равна 0,9. Для специалиста средней
квалификации эта вероятность равна 0,8. Взятый наудачу
прибор оказался надёжным. Найти вероятность того, что
этот прибор собран специалистом высшей квалификации.

111.

Событие А: Взятый наудачу прибор оказался надёжным.
Гипотеза H1
– появление прибора,
специалистом высшей квалификации.
Гипотеза H2 – появление прибора,
специалистом средней квалификации.
P(H1) = 0,3
P(A/H1) = 0,9
P(H2) = 0,7
P(A/H2) = 0,8
P(A) = 0,3·0,9 + 0,7·0,8 = 0,83
P(H1/A) = 0,3·0,9 / 0,83 ≈ 0,325
собранного
собранного

112.

Последовательность независимых
испытаний.
Формула Бернулли
Пусть относительно некоторого случайного
события А проводится п испытаний, в одних и тех
же условиях, в силу чего вероятность наступления
события А остается одной и той же в каждом
испытании, т.е. испытания независимые.
Обозначим эту вероятность через р.

113.

Какова вероятность того, что при этих п
испытаниях событие А произойдет т раз?
(т – любое число, заключенное между нулем и п)
n m
m m
Pm,n Cn p 1 p
m
n!
p qn m
m ! n m !

114.

Пример. Стрелок стреляет по цели пять раз
подряд. Вероятность поражения цели этим
стрелком при одном выстреле равна 0,8.
Какова вероятность того, что цель будет поражена
четыре раза?
4 1
4
P C 0,8 0,2 0,4096 0,41
4,5 5

115.

Пример
Каждый день акции корпорации АВС поднимаются в
цене или падают в цене на один пункт с вероятностями
соответственно 0,75 и 0,25. Найти вероятность того, что
акции после шести дней вернутся к своей
первоначальной цене. Принять условие, что изменения
цены акции вверх и вниз – независимые события.
РЕШЕНИЕ:
Для того, чтобы акции вернулись за 6 дней к своей
первоначальной цене, нужно, чтобы за это время они 3
раза поднялись в цене и три раза опустились в цене.
P6(3) = C36(3/4)3(1/4)3 = 0,13

116.

Случайной
величиной
Случайное
событиеназывается величина,
которая
можетхарактеристика
в зависимости от исходов
качественная
испытания
принимать те или иные
испытания
случайные значения Случайная величина
Обозначениеколичественная
С.В.: X,Y, Z характеристика
испытания
Значения С.В.: x, y, z
Вероятность С.В.:
P x P X x

117.

Случайные величины
Случайная дискретная величина - это
такая величина ,число возможных
испытаний которой либо конечно,
либо бесконечное множество,
но обязательно счетное

118.

Примеры ДСВ
1. Частота попаданий при 3 выстрелах – X
x1=0, x2=1, x3=2, x4=3
2. Игрок бросает монету – при выпадении
герба он выигрывает 100 рублей, решки –
проигрывает 100 рубль. Случайная величина
Х–выигрыш
игрока
будет
принимать
значения +100 или -100 в зависимости от
того, чем закончится эксперимент – гербом
или решкой.

119.

Примеры ДСВ
3. Эксперимент – одновременное бросание
двух
игральных
кубиков,
случайная
величина – сумма выпавших очков, может
принимать все целые значения от 2 до 12 в
зависимости от выпавшей комбинации.

120.

Случайные величины
Случайной непрерывной величиной
называется такая величина, возможные
значения которой непрерывно заполняют
некоторый интервал (конечный или
бесконечный).
Число всех возможных значений НСВ
бесконечно

121.

Примеры НСВ
1. Случайное отклонение по дальности точки
падения снаряда от цели
2.
Продолжительность
электрической лампы
работы
3. Дальность полета снаряда, уровень воды
в половодье и т.д.

122.

Числовые характеристики
ДСВ

123.

Математическое ожидание Д.С.В.
Х
р
x1
x2
…
xn
p1
p2
…
pn
n
m x M ( X ) x1 p1 x 2 p 2 ... x n p n xi pi
i 1

124.

Свойства
математического ожидания Д.С.В.
1) М (С ) С
Теорема. M X
x1 x2 ... xn
n

125.

2) M (C Х ) C M ( Х )

126.

3) M ( X Y ) M ( X ) M (Y )
независимые
4) M ( X Y ) M ( X ) M (Y )

127.

Теорема. М(Х) числа появления события
А в п независимых испытаниях равно
произведению числа испытаний
на вероятность появления события в
каждом испытании.
M ( X ) np

128.

X M (X )
D ( X ) M X M ( X )
2
Дисперсия
С.В.
отклонение
значений
?
случайной величины от М(Х)
2
2
2
2
X M X x1 M X x2 M X … xn M X
p
p2
p1
2
…
pn
2
D X x1 M X p1 x2 M X p2 ...
2
... xn M X pn

129.

Свойства дисперсии Д.С.В.
1)
D (C ) 0
2) D(CX ) C D( X )
2
3) D( X Y ) D( X ) D(Y )

130.

Теорема. Дисперсия числа появления
σ X D X
события А в п независимых испытаний,
в каждом из которых вероятность р
появления события постоянна, равна
произведению числа испытаний
на вероятности появления и
не появления события
в каждом испытании
D( X ) npq

131.

Способы вычисления дисперсии Д.С.В.
1) D( X ) M X M ( X )
2
2) D( X ) M ( X ) M ( X )
2
2

132.

Законы распределения ДСВ

133.

Способы задания закона распределения
а) таблицей - рядом распределения
1

134.

б) Графическое представление этой
таблицы – многоугольник
распределения
0,4
0,35
0,3
0,25
0,2
0,15
0,1
0,05
0
0
1
2
3
4
5

135.

Законы распределения ДСВ
2.
Закон распределения
1.Биноминальный
законПуассона
распределения
m mn m
m
P C p q e
P X nm
m!
q
1
p
n p 10
р 0,1
n

136.

Числовые характеристики
НСВ

137.

Математическое ожидание Н.С.В.
M (X )
x f ( x)dx
Дисперсия Н.С.В.
D( X )
x
f
(
x
)
dx
[
M
(
X
)]
2
2

138.

Среднее квадратичное отклонение
( X ) D ( X )
Модой (М0) Д.С.В. называется
ее наиболее вероятное значение
Модой (М0) Н.С.В. называется
такое значение случайной величины,
при которой плотность распределения
имеет максимум
f ( M 0 ) max

139.

Пусть х – действительное число.
1
Вероятность
0,8 события, состоящего в том,
что Х примет
0,6 значение, меньшее х,
0,4
т.е. Х < x, обозначим
через
F(x)
0,2
0
Функция распределения
0
1
2
3
4
0,084Интегральная
0,386 0,766 0,964
1
Функция
функция
распределения
F ( x) P( X x)

140.

b
Свойства
плотности
распределения
f ( x) F ( x)
P (a X b) f ( x)dx
-плотность
распределения
a
1. f ( x ) 0
вероятности Н.С.В. Х
2.
f ( xF)(dx
x) 1
x
f ( x)dx
a sin x, при 0 x
f ( x)
при x 0 или
0,
x

141.

при
x a
0,
Законы
распределения
Н.С.В.
x a
1.Равномерное
распределение
на
F ( x)
, при a x b
a b]
отрезке
b [a,
0, x a
1,
при
x b
f ( x) C , a x b
0, x b

142.

2. Показательное распределение
вероятностей Н.С.В. Х
при x 0
0,
f ( x ) x
e , при x 0
- положительное число
при x 0
0,
F ( x)
x
при x 0
1 e

143.

3. Нормальный закон распределения
f ( x)
F ( x)
1
x 2
1
( x mx ) 2
e
x
e
x 2
2 x2
( x mx ) 2
2 2x
dx

144.

Пример. Задана Н.С.В. Х
своей плотностью распределения f(x).
A
cos
2
x
,
при
x
4
4
f ( x)
0,
при
x
4

145.

1. Определить коэффициент А.
2. Найти функцию распределения.
3. Построить графики
функции распределения и плотности
распределения.
4. Определить вероятность того,
что случайная величина Х попадет
в интервал 6 ; 2
5. Найти математическое ожидание,
дисперсию и
среднее квадратичное отклонение.