Similar presentations:
Теория вероятностей и математическая статистика. Лекция 3
1. Теория вероятностей и математическая статистика
ГУ ЛНР «Луганский государственный медицинскийуниверситет им. Святителя Луки»
кафедра медицинской, биологической физики и
информатики
Лекция 3 по дисциплине «Физика, математика» по теме
Теория вероятностей и
математическая статистика
Лектор: к.п.н, доц. Березкина И.А.
Луганск, 2020
2. История развития теории вероятностей
• Становление теории вероятностейотносится к эпохе Возрождения в
Италии (15 век):
- итальянец Кардано (16 век),
«Книга об игре в кости»
- Галилео Галилей (16-17 века),
«О выходе очков при игре в кости»
• Считается, что теория вероятностей зародилась как
наука в переписке двух ученых Б. Паскаля и П. Ферма
(17 век)
• Якоб Бернулли, который в 1713 г. выпустил книгу
«Искусство предположений»
• А.Н. Колмогоров в 1933 г. – аксиоматическое
построение теории вероятностей ...
2
3. Основные определения
Испытание - выполнение определенного комплексаусловий, в которых наблюдается то или иное
явление, фиксируется тот или иной результат.
Def Событие есть результат испытания.
Виды событий:
–Достоверное, которое обязательно
произойдет при определенной совокупности
условий.
–Невозможное, которое заведомо
не произойдет.
–Случайное, которое может либо
произойти, либо не произойти.
3
4. Виды случайных событий
4Виды случайных событий
• События называют несовместными, если
появление одного из них исключает
появление других событий в одном и том
же испытании. В противном случае это
совместные события.
•События называют равновозможными, если есть
основания считать, что ни одно из них не является
более возможным, чем другое.
•Несколько событий образуют полную группу, если
в результате испытания появится хотя бы одно из
них.
Пример: бросание игральной кости W = {1, 2, 3, 4, 5, 6}
5. Классическое определение вероятности
5Классическое определение вероятности
• Вероятностью события А называется
отношение числа m случаев,
благоприятствующих этому событию
(т.е. приводящих к наступлению события А),
к общему числу случаев n:
m
P( A)
n
6. Свойства вероятности
6Свойства вероятности
• Свойство 1. Вероятность достоверного
события равна единице.
• Свойство 2. Вероятность невозможного
события равна нулю.
• Свойство 3. Вероятность случайного
события есть положительное число,
заключенное между нулем и единицей.
0 P( A) 1
7.
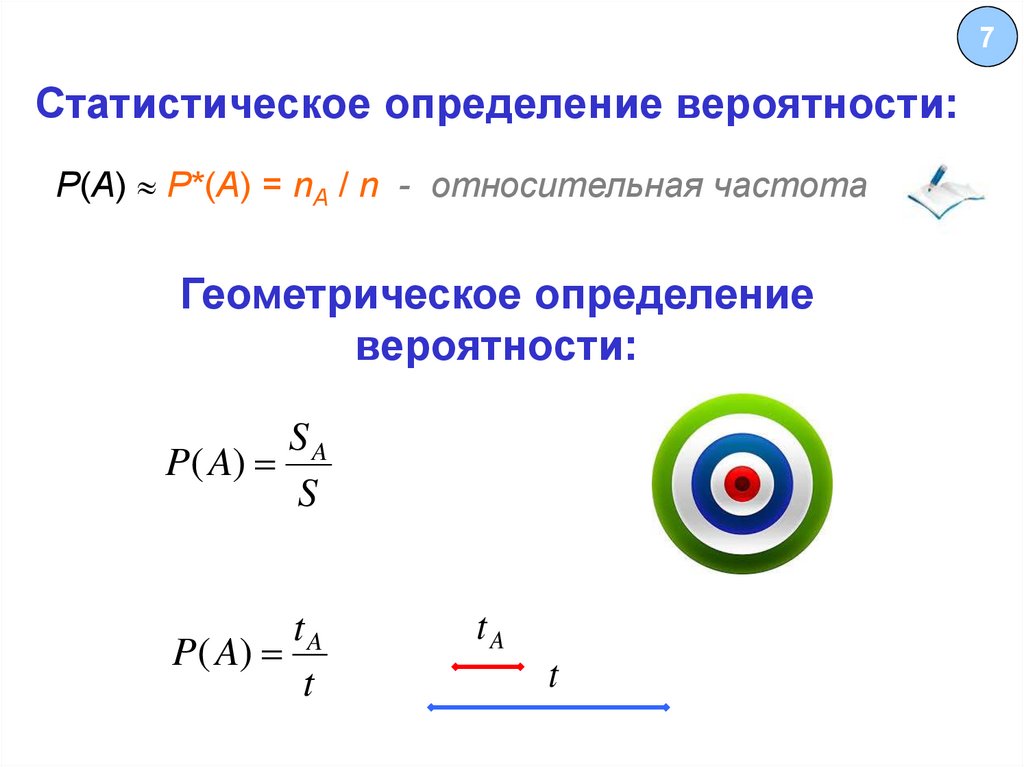
7Статистическое определение вероятности:
Р(А) P*(A) = nА / n - относительная частота
Геометрическое определение
вероятности:
SA
P( A)
S
tA
P( A)
t
tA
t
8. Условная вероятность
8Условная вероятность
Условной вероятностью события В при условии,
что произошло событие А называется отношение
вероятности произведения этих событий к
вероятности события А, причем Р(А) 0:
P( A B)
P( B / A)
P( A)
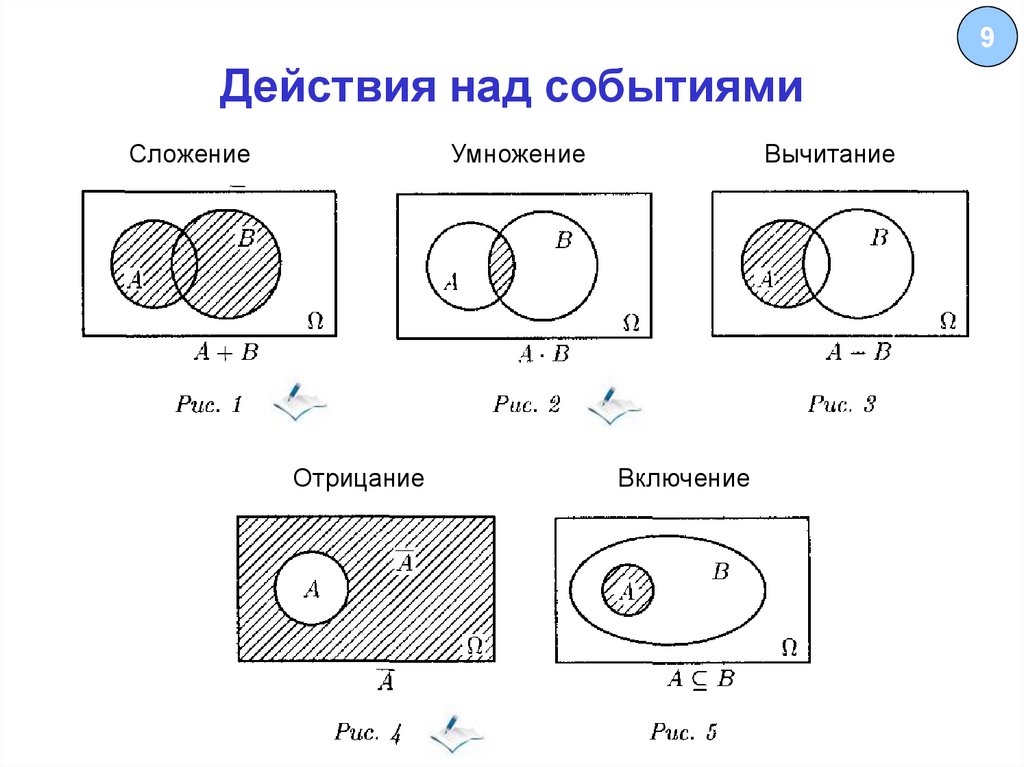
9. Действия над событиями
9Действия над событиями
Сложение
Умножение
Отрицание
Вычитание
Включение
10. Вероятность произведений событий
10Вероятность произведений событий
Теорема умножения вероятностей
Вероятность произведения двух событий равна
произведению вероятности одного из них на
условную вероятность другого при условии, что
первое событие произошло:
P( A B) P( А) P( В / А)
11. Независимые события
11Независимые события
Событие А называется
независимым от события В,
если его условная вероятность
равна безусловной Р(А / В) = Р(А).
Теорема умножения вероятностей
для независимых событий:
P( A B) P( A) P( B)
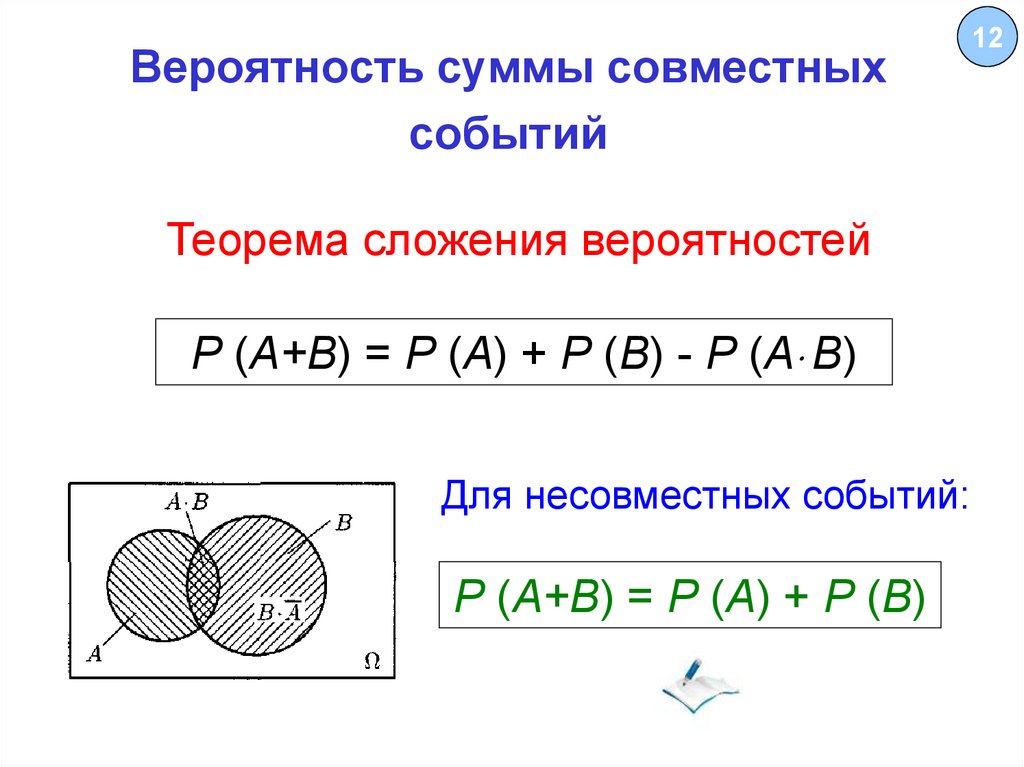
12. Вероятность суммы совместных событий
Теорема сложения вероятностейР (А+В) = Р (А) + Р (В) - Р (А В)
Для несовместных событий:
Р (А+В) = Р (А) + Р (В)
12
13.
13Предмет математической статистики
В широком смысле статистика является
наукой, изучающей массовые явления
протекающие в совокупностях некоторых
факторов или явлений.
Статистика в узком смысле представляет
собой метод обработки данных индивидуальных
наблюдений.
14.
14Этапы статистического исследования
1. Сбор информации
2. Обработка информации
3. Анализ данных
15. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
15СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Def Случайной называют величину, которая в
результате испытания примет одно и только
одно возможное значение, наперед не
известное и зависящее от случайных причин.
Виды случайных величин:
•Дискретной называют случайную
величину, которая принимает
отдельные, изолированные возможные
значения с определенными
вероятностями.
•Непрерывной называют случайную
величину, которая может принимать
все значения из некоторого конечного
или бесконечного промежутка.
16. Закон распределения случайной величины
Пусть Х – дискретная случайная величина,принимающая значения х1, х2,…. с некоторыми
вероятностями рi
Способы задания закона распределения:
• формула рi = Р {X=xi }
• таблица распределения (или ряд распределения)
16
17. Функция распределения
17Функция распределения
• Функцией распределения случайной
величины Х называется функция F(х),
которая для любого х равна вероятности
события { X < x }:
F(х) = Р { X < x }
F (x < - ) = 0
F (x < + ) = 1
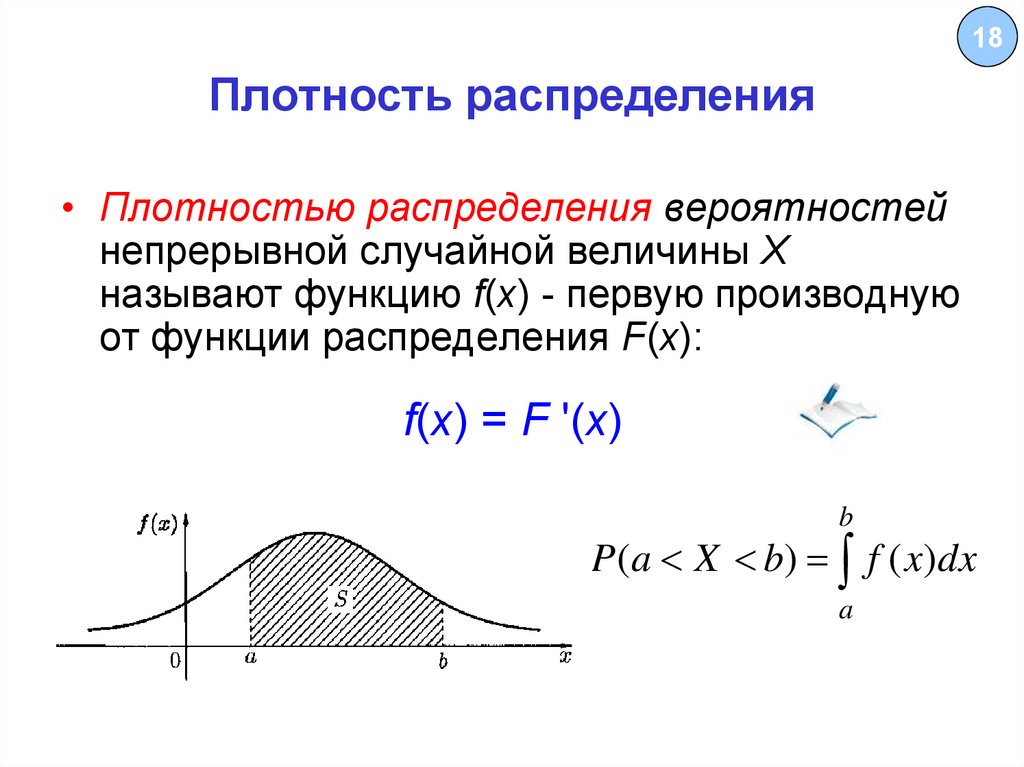
18. Плотность распределения
18Плотность распределения
• Плотностью распределения вероятностей
непрерывной случайной величины X
называют функцию f(х) - первую производную
от функции распределения F(х):
f(х) = F '(х)
b
P(a X b) f ( x)dx
a
19. Математическое ожидание
Математическим ожиданием дискретной
случайной величины Х называется число,
равное сумме произведений всех ее значений
на соответствующие им вероятности
n
M [ X ] xi pi
i 1
• Математическим ожиданием непрерывной
случайной величины X с плотностью вероятности f(x),
возможные значения которой принадлежат отрезку
[а, b], называют определенный интеграл
b
M [ X ] x f ( x)dx
a
19
20. Дисперсия
• Дисперсией случайной величины Хназывается математическое ожидание
квадрата ее отклонения от своего
математического ожидания.
• Дисперсия характеризует разброс значений
случайной величины относительно ее
математического ожидания.
D[ X ] xi M [ X ] 2 pi
i
20
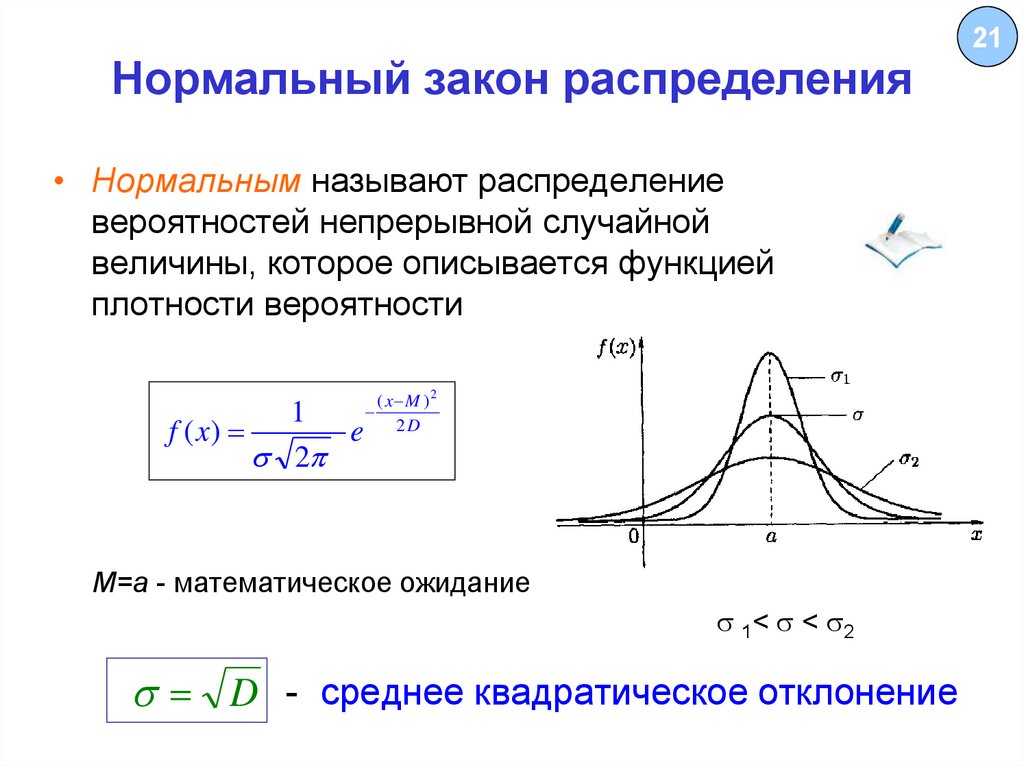
21. Нормальный закон распределения
• Нормальным называют распределениевероятностей непрерывной случайной
величины, которое описывается функцией
плотности вероятности
f ( x)
1
e
2
( x M )2
2D
M=a - математическое ожидание
1< < 2
D - среднее квадратическое отклонение
21
22.
22Мыслимое множество всех изучаемых
объектов называется генеральной совокупностью.
Выборка - это последовательность
чисел x1, . . . , xn , полученных при nкратном повторении эксперимента в
неизменных условия.
Характеристики выборки (среднее,
дисперсия) являются приблизительными
оценками истинных параметров неизвестного
нам генерального распределения.
23. Центральная тенденция
Измерение центральной тенденции заключается ввыборе числа, которое наилучшим способом
описывает все значения признака набора данных.
Среднее значение:
n
xi
x i 1
n
Главная цель среднего – обобщение набора
данных для их последующего анализа,
сопоставления и сравнения.
23
24.
Дисперсия – основная характеристикаразброса случайной величины около
среднего.
n
( xi x)
s 2 i 1
2
n 1
Корень из дисперсии называется
стандартным отклонением (std).
s
s2
24
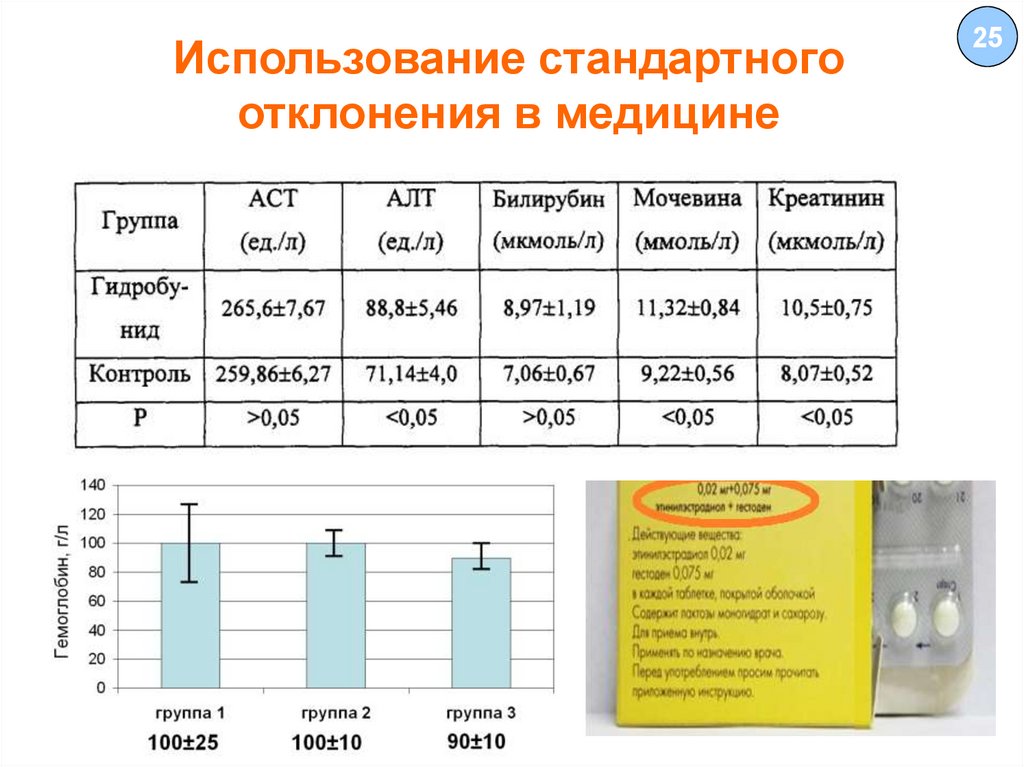
25.
Использование стандартногоотклонения в медицине
25
26.
26Доверительный интервал
генерального среднего
• Доверительным интервалом
для среднего значения является
интервал значений вокруг оценки,
где с данным уровнем доверия
находится "истинное" среднее
популяции.
• расчет границ генерального среднего
s
X x Δx x tкр
n
X x
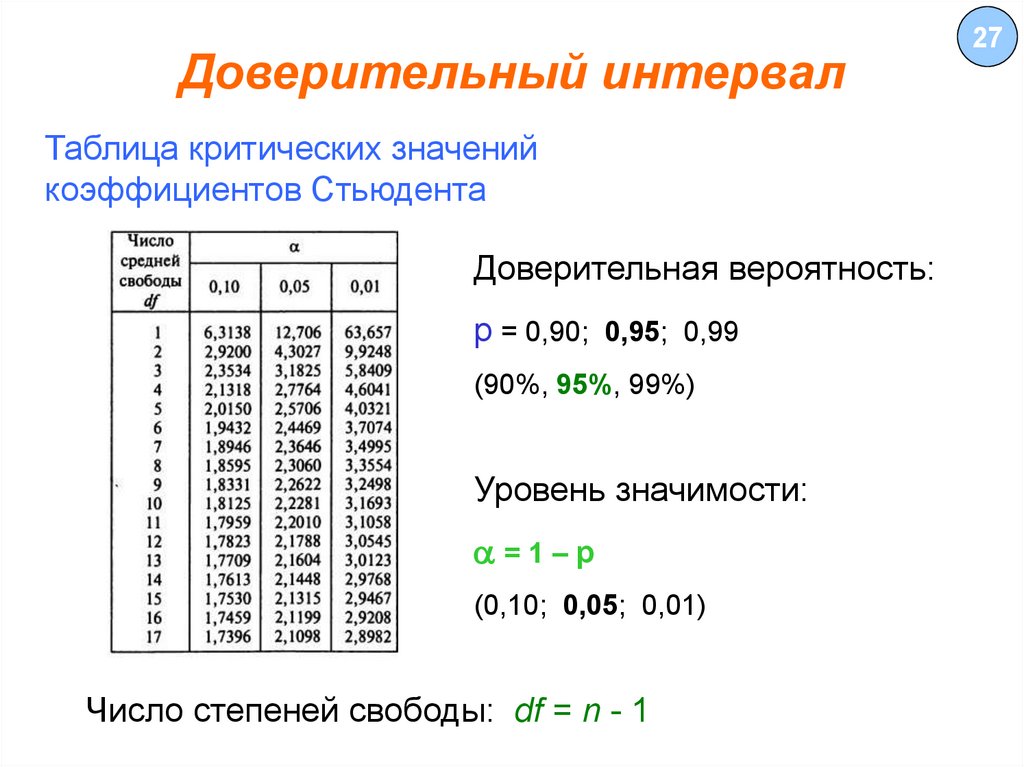
27.
Доверительный интервалТаблица критических значений
коэффициентов Стьюдента
Доверительная вероятность:
p = 0,90; 0,95; 0,99
(90%, 95%, 99%)
Уровень значимости:
a=1–p
(0,10; 0,05; 0,01)
Число степеней свободы: df = n - 1
27
28.
Литература1. Лобоцкая Н.Л. Основы высшей математики.
2. Тимонюк В.А. Биофизика.
3. Ремизов А.Н. Медицинская и биологическая физика.
4. Чалий О.В. Медична і біологічна фізика.





















 mathematics
mathematics








