Similar presentations:
Основы теории вероятностей и математической статистики. Лекция 12
1.
ПРАКТИЧЕСКАЯ ФИЗИКАДоцент кафедры
экспериментальной физики
Ерина Марина Васильевна
2.
Лекция № 12Основы теории вероятностей и математической
статистики
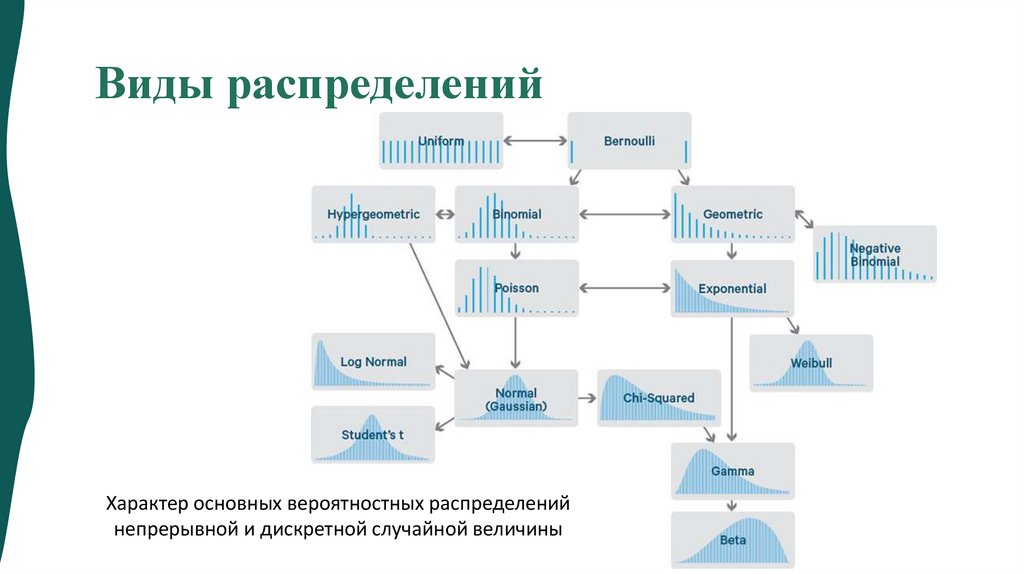
• Функция распределения. Плотность вероятности.
Математическое ожидание и дисперсия.
• Распределения в физике
3.
Функция распределения. Плотностьвероятности. Математическое ожидание и
дисперсия
Интегральным законом распределения или функцией распределения случайной величины X
называется функция F(x), равная вероятности того, что случайная величина X принимает
значение меньшее x:
F ( x) P( X x)
В случае дискретных случайных величин: F ( x)
p i – вероятности значений xi
p
xi x
i
F(x) – монотонно возрастающая функция
P(a x b) F (b) F (a )
В предельном случае интегральная функция распределения имеет вид гладкой кривой
4.
xЕсли физическая величина X непрерывная:
F ( x ) f ( x ) dx
Вероятность того, что случайная величина примет значение в интервале [a, b]:
b
P(a x b) f ( x)dx
a
f(x) – дифференциальный закон распределения случайной величины – функция
плотности вероятности.
Условие нормировки функции плотности вероятности:
f ( x)dx 1
5.
Математическое ожидание случайной величины x есть среднее значение x сучетом вероятности осуществления каждого значения x.
n
Для дискретного распределения: M ( x) xi pi
i 1
Для непрерывного распределения:
x M ( x) x f ( x)dx
Если задана какая-либо функция переменной
математическое ожидание этой функции:
x,
например
h(x),
то
M (h( x)) h( x) f ( x)dx
M ( x 2 ) x 2 f ( x)dx
Например: Математическое ожидание функции х2 равно:
Дисперсией случайной величины x называют
2
математическое ожидание функции x x :
M x x 2 x
2
6.
Распределение Пуассонаn
n
n!
p k q n k n p
В распределении Бернулли: k k P k
k!(n k )!
k 0
k 0
2 np 1 p npq
k
n
В классическом виде распределение Бернулли в физике применяется редко.
Чаще используется распределение Пуассона, которое является частным случаем
биномиального распределения при условии p 0, а n . Второе название
распределения Пуассона – закон редких явлений.
a n a
Pa (n)
e
n!
n=0, 1, 2 …
7.
Математическое ожидание:a n a
M ( n) n e a n
n!
Дисперсия:
a
2 a
8.
Распределение Пуассона описывает распределение результатов в эксперименте,когда ведется счет событий, происходящих случайно, но в определенном
ожидаемом среднем темпе.
Пример: подсчет радиоактивных ядер и подсчет частиц космических лучей.
Пусть студент А утверждает, что он измерил число частиц космических лучей,
упавших на счетчик Гейгера за одну минуту. И нашел, что в среднем 9 частиц
проходит через счетчик.
Студент Б также считает число частиц за одну минуту и получает в среднем 12.
Кто же прав?
Студентка В считает число частиц упавших за 10 минут. Регистрирует 120 частиц.
Если прав А, то 9 ± 9 = 9 ± 3
Вероятность любого результата









 mathematics
mathematics








