Similar presentations:
Лекция_10_Функции_Пределы
1.
Понятие функции.Предел,
непрерывность
2.
Функция – это зависимость переменной уот переменной х, причем каждому
значению х соответствует только
одно значение у.
y = f (x) - функция
x – аргумент, или
независимая переменная
y – значение функции, или
зависимая переменная
3.
Термин «функция» - от латинскогоfunctio - совершение, выполнение
Первоначально понятие функции как
выражения сложилось в 17 веке
В 18 веке основным объектом
изучения
математики стали зависимости между
переменными величинами
4.
y = f (x) - функцияx – аргумент, или
независимая переменная
y – значение функции, или
зависимая переменная
5.
Область определения функцииОбластью определения (существования)
функции называется множество всех
действительных значений аргумента, при
которых она может иметь действительное
значение.
Например, для функции у=х областью
определения является множество всех
действительных значений чисел R ;
для функции у=1/х областью определения
является множество R кроме х=0.
6.
Общая схема исследования функции1. Область определения функции.
2.Исследование области значений функции.
3. Исследование функции на четность.
4.Исследование промежутков возрастания и убывания
функции.
5. Исследование функции на монотонность.
5. Исследование функции на экстремум.
6. Исследование функции на периодичность.
7. Определение промежутков знакопостоянства.
8.Определение точек пересечения графика функции с осями
координат.
9. Построение графика функции.
7.
Множество значений функции.Множеством значений функции
называется множество всех
действительных значений
функции у, которые она может
принимать. Например,
множеством значений функции
у= х+1 является множество R.
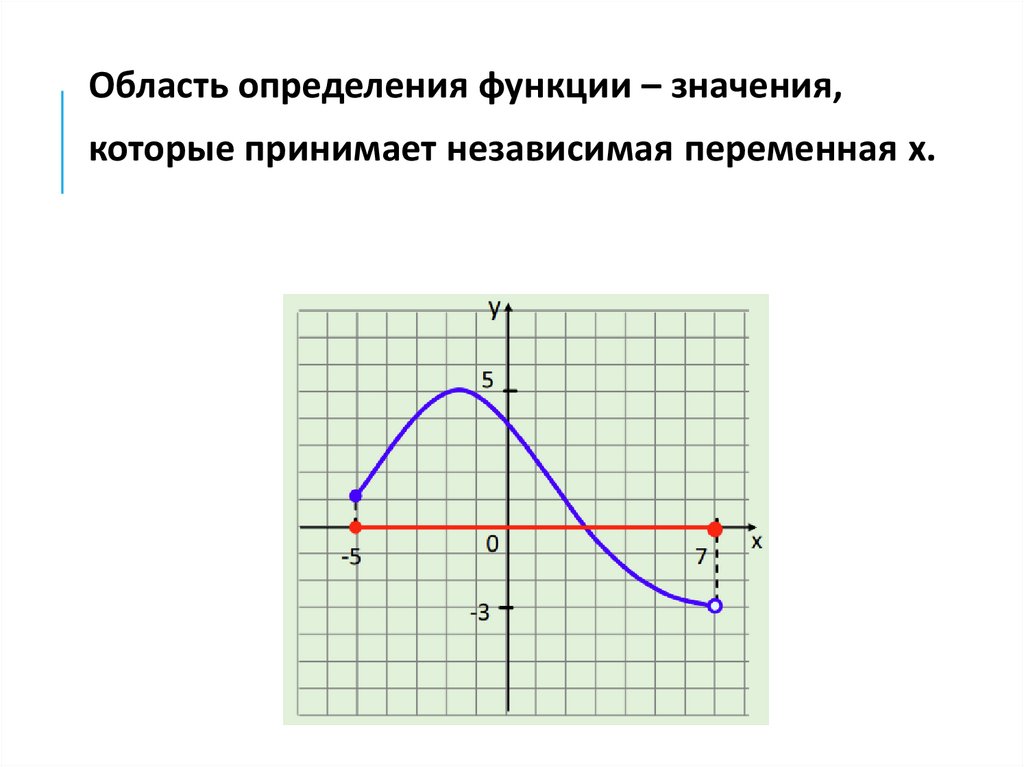
8.
Область определения функции – значения,которые принимает независимая переменная х.
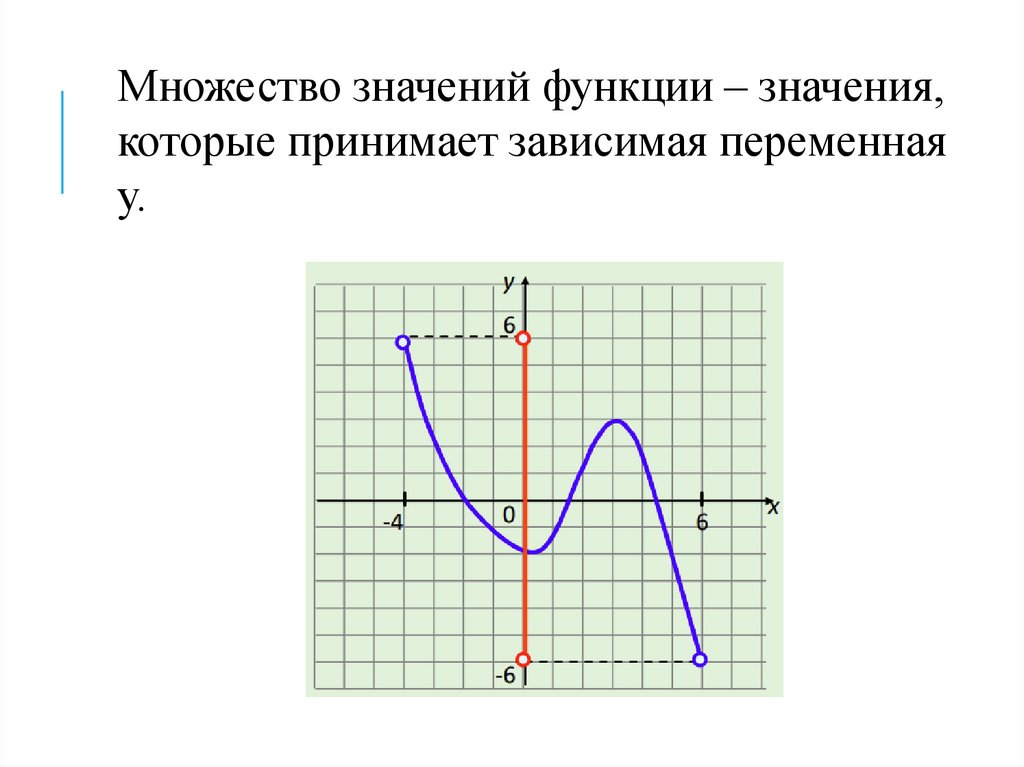
9.
Множество значений функции – значения,которые принимает зависимая переменная
у.
10. Алгоритм описания свойств функций
СВОЙСТВА ФУНКЦИИАЛГОРИТМ ОПИСАНИЯ СВОЙСТВ ФУНКЦИЙ
Область определения
Область значений
Четность
Монотонность
Непрерывность
Ограниченность
Наибольшее и наименьшее значения
Нули функции
Выпуклость
11. Рассмотрим свойства функций:
СВОЙСТВА ФУНКЦИЙРАССМОТРИМ СВОЙСТВА ФУНКЦИЙ:
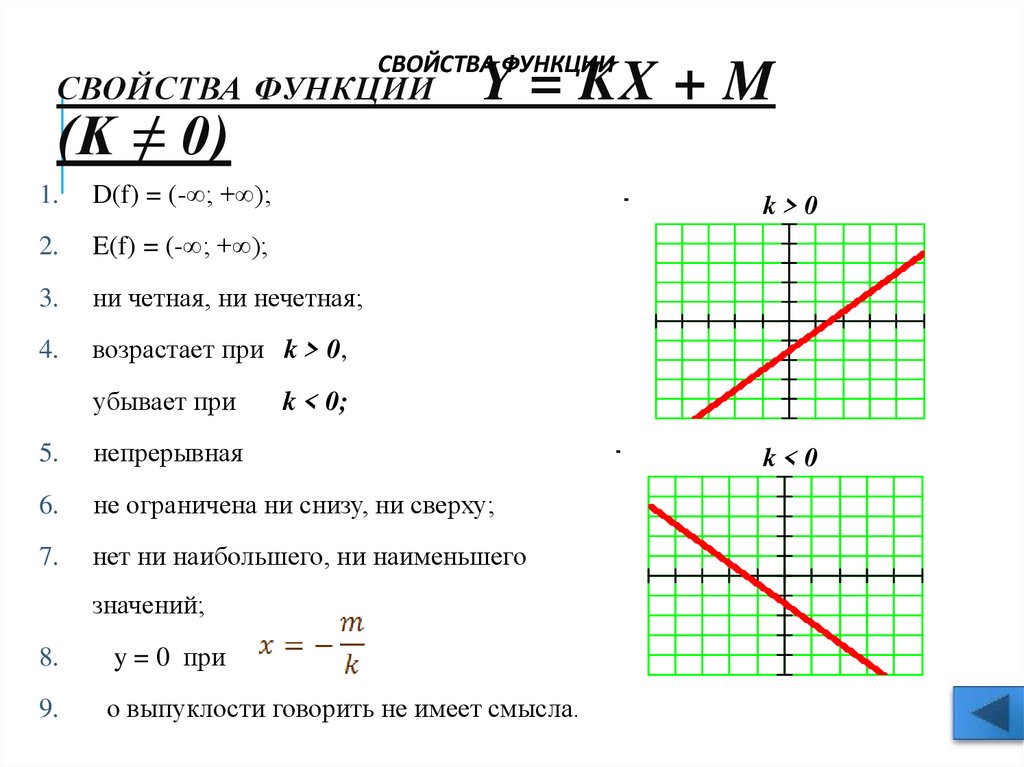
12. Свойства функции y = kx + m (k ≠ 0)
СВОЙСТВА ФУНКЦИИСВОЙСТВА ФУНКЦИИ
(K ≠ 0)
1.
D(f) = (-∞; +∞);
2.
E(f) = (-∞; +∞);
3.
ни четная, ни нечетная;
4.
возрастает при k > 0,
убывает при
Y = KX + M
k>0
k < 0;
5.
непрерывная
6.
не ограничена ни снизу, ни сверху;
7.
нет ни наибольшего, ни наименьшего
значений;
8.
y = 0 при
9.
о выпуклости говорить не имеет смысла.
k<0
13.
Предел и непрерывностьфункции
14. Бесконечно малая и бесконечно большие величины.
БЕСКОНЕЧНО МАЛАЯ И БЕСКОНЕЧНОБОЛЬШИЕ ВЕЛИЧИНЫ.
Переменная величина α называется бесконечно малой, если
она изменяется так, что какое бы малое положительное число ℰ
ни взято , ∣α∣ становится и при дальнейшем изменении
величины α остается меньше ℰ.
α→0
1
1
1
1
: 1; ; ; ; ;...
2
3
4
5
-1
0
или
: 1;
1
1 1
;
;
2 3
1 1
;
;...
4 5
15.
Переменная величина у называется бесконечно большой, еслиона изменяется так, что какое бы большое положительное число
N ни взято , ∣у∣ становится и при дальнейшем изменении
величины у остается больше N.
у→∞
или
y : 2; 4; 6; 8; ...
0
y : 2; 4; 6; 8; ...
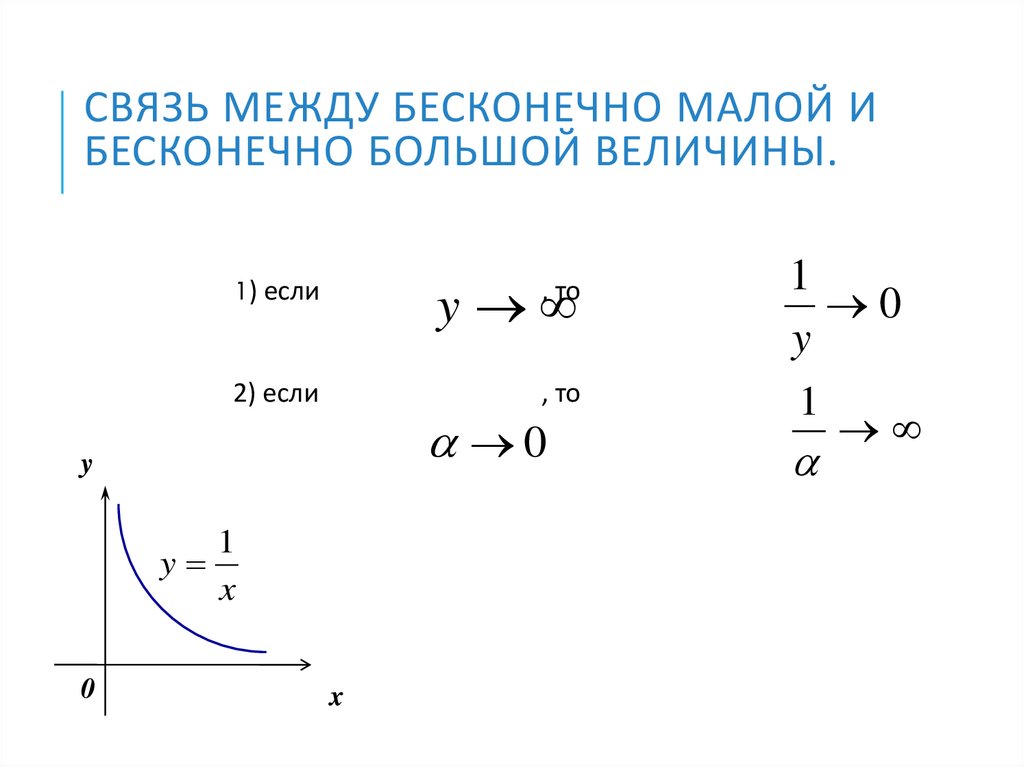
16. Связь между бесконечно малой и бесконечно большой величины.
СВЯЗЬ МЕЖДУ БЕСКОНЕЧНО МАЛОЙ ИБЕСКОНЕЧНО БОЛЬШОЙ ВЕЛИЧИНЫ.
1) если
y
2) если
, то
, то
0
y
y
0
1
x
x
1
0
y
1
17. пример:
ПРИМЕР:1)
, тогда
y : 1, 10, 100, 1000, ...
1
: 1 0,1 0,01 0,001 ... 0
y
2) : 1 0,1 0,01 , 0тогда
,001 ... 0
1
: 1, 10, 100, 1000, ...
18. Предел переменной
ПРЕДЕЛ ПЕРЕМЕННОЙx : 3,1 3,01 3,001 3,0001 ... 3
x 3 : 0,1 0,01 0,001 0,0001 ... 0
Число 3 называется пределом переменной х:
lim x 3
или
x 3
19. Постоянная а называется пределом переменной х, если разность между ними есть бесконечно малая величина α�, т.е
• ПОСТОЯННАЯА
НАЗЫВАЕТСЯ
ПРЕДЕЛОМ
ПЕРЕМЕННОЙ Х, ЕСЛИ РАЗНОСТЬ МЕЖДУ НИМИ
ЕСТЬ БЕСКОНЕЧНО МАЛАЯ ВЕЛИЧИНА Α , Т.Е
lim x a , если
x a
lim 0
lim y
или
x a 0
20. Предел функции
ПРЕДЕЛ ФУНКЦИИy x 4
2
x : 3,1 3,01 3,001 3,0001 ... 3
y : 5,6 5,06 5,006 5,0006 ... 5
lim x2 4 5
x 3
21.
Определение «на языке последовательности»Число а называется пределом функции f(x) в
точке х=х0, если для всех значений х, достаточно
близких к х0 (х→х0) и отличных от х0 (х≠х0),
значение функции f(x) сколь угодно мало
отличается от числа а (f(x)→а), т.е
lim f ( x) a
x x0
или
f ( x) a
при
x x0
22.
предел функции в точке ипредел функции на бесконечности
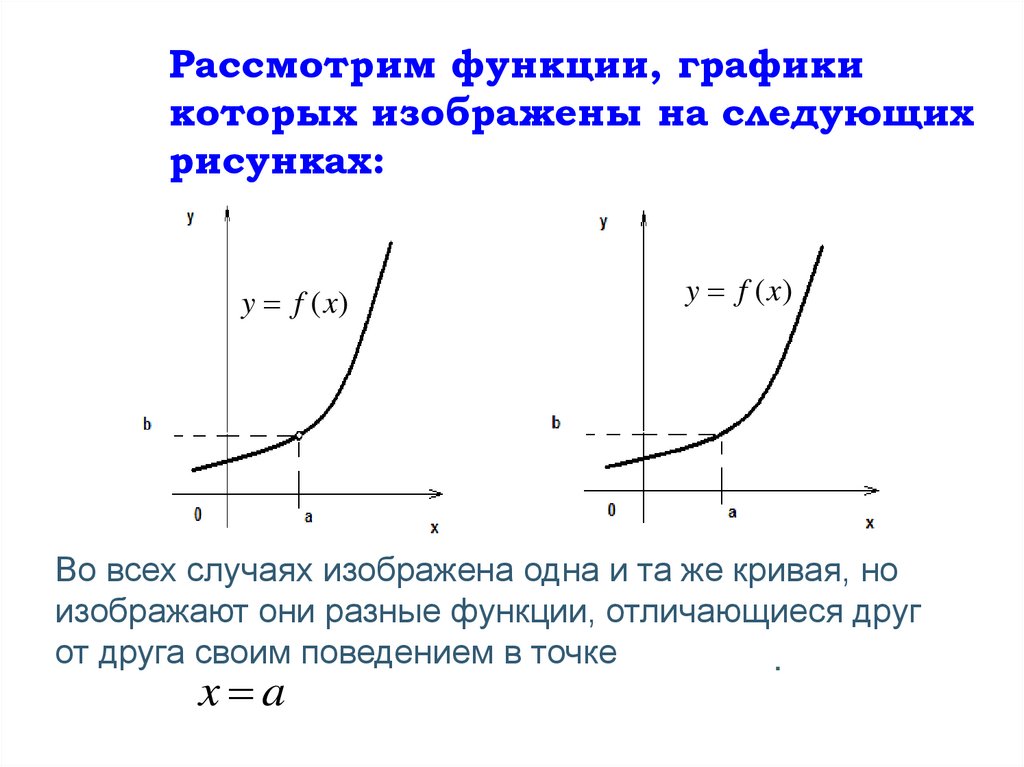
23.
Рассмотрим функции, графикикоторых изображены на следующих
рисунках:
y f (x)
y f (x)
Во всех случаях изображена одна и та же кривая, но
изображают они разные функции, отличающиеся друг
от друга своим поведением в точке
.
x a
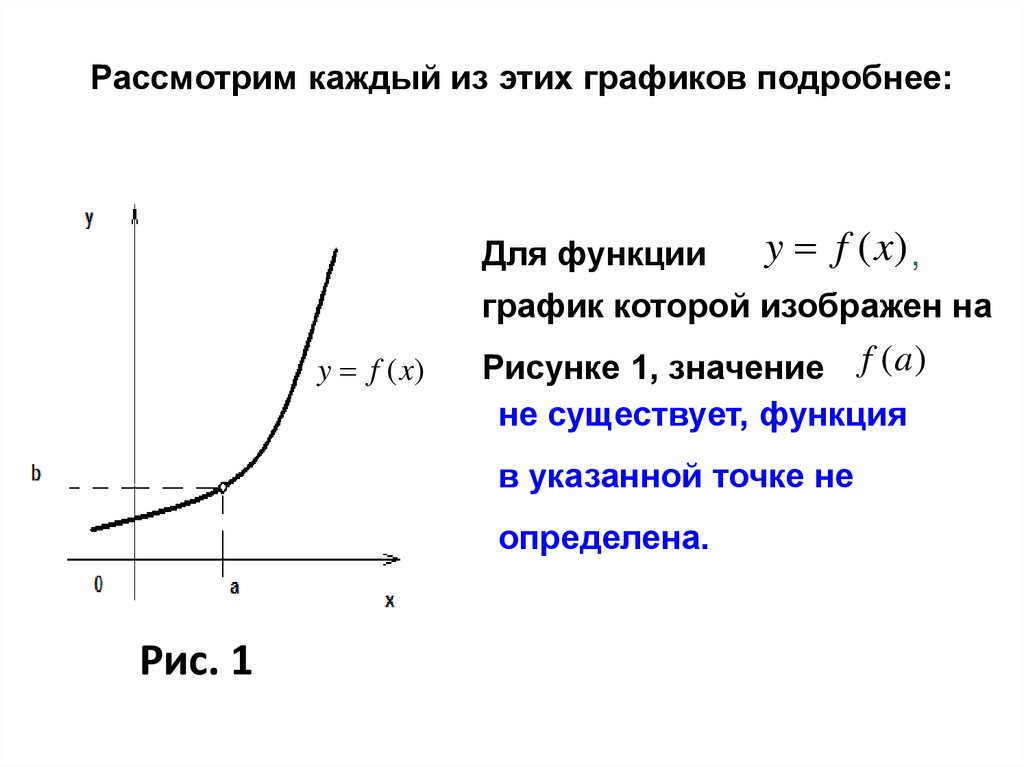
24.
Рассмотрим каждый из этих графиков подробнее:Для функции
y f (x) ,
график которой изображен на
y f (x)
Рисунке 1, значение f (a )
не существует, функция
в указанной точке не
определена.
Рис. 1
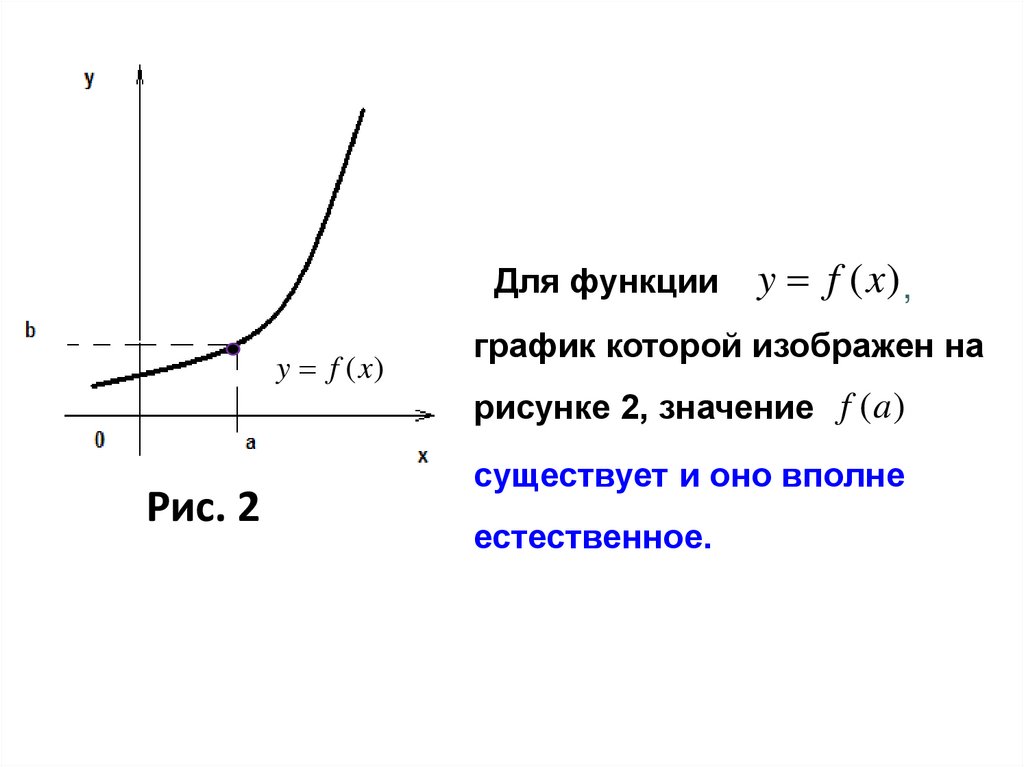
25.
Для функцииy f (x)
y f (x) ,
график которой изображен на
рисунке 2, значение f (a )
Рис. 2
существует и оно вполне
естественное.
26.
Для всех случаев используется одна и таже запись:
lim f ( x) b,
x а
которую читают: «предел функции
y f (x)
при стремлении
x
к a равен b ».
27.
Содержательный смысл этой фразы следующий:если значения аргумента выбирать все ближе и ближе к
значению x a , то значения функции
все меньше и меньше
отличаются от предельного значения
b.
Или
в достаточно малой окрестности точки a
справедливо приближенное равенство:
f ( x) a
При этом сама точка x a исключается из рассмотрения.
28.
если предел функцииy f (x) при стремлении х к
функции в точке
a равен значению
x a , то в таком случае
функцию называют непрерывной.
График такой функции представляет собой
сплошную линию, без «проколов» и «скачков».
29.
Функцию y f (x)называют непрерывной
на промежутке
X , если она непрерывна в
каждой точке этого промежутка.
Примерами непрерывных функций на всей числовой
2
y
ax
by c,
y
kx
b
,
y
C
,
прямой являются:
y | x |, y x n , n ,
Функция
y x непрерывна на луче [0, ), а
n
y
x
, n непрерывна на промежутках
функция
( , 0) (0, ).
30. Предел функции в точке
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕПусть функция y = f(x) определена в некоторой окрестности точки
x0, кроме, самой точки x0.
Число А называют пределом функции в точке x0 (или при x x0),
если для любого положительного ε найдется такое положительное
число δ, что для всех х из δ – окрестности точки x0 справедливо
неравенство:
f (x) A
0; 0; x : x x0 f ( x ) A
lim f ( x ) A
x x0
31. Теорема.
ЕСЛИ ФУНКЦИЯ F (X) ИМЕЕТ ПРЕДЕЛ В ТОЧКЕХ0, ТО ЭТОТ ПРЕДЕЛ ЕДИНСТВЕННЫЙ.
32. Бесконечно малая функция и бесконечно большая функция.
Функция α (x) называется бесконечномалой при x → a (здесь a – конечное
число или ∞), если
Функция f(x) называется бесконечно
большой функцией (или бесконечно большой
величиной) при х→а, если lim f ( x)
x a
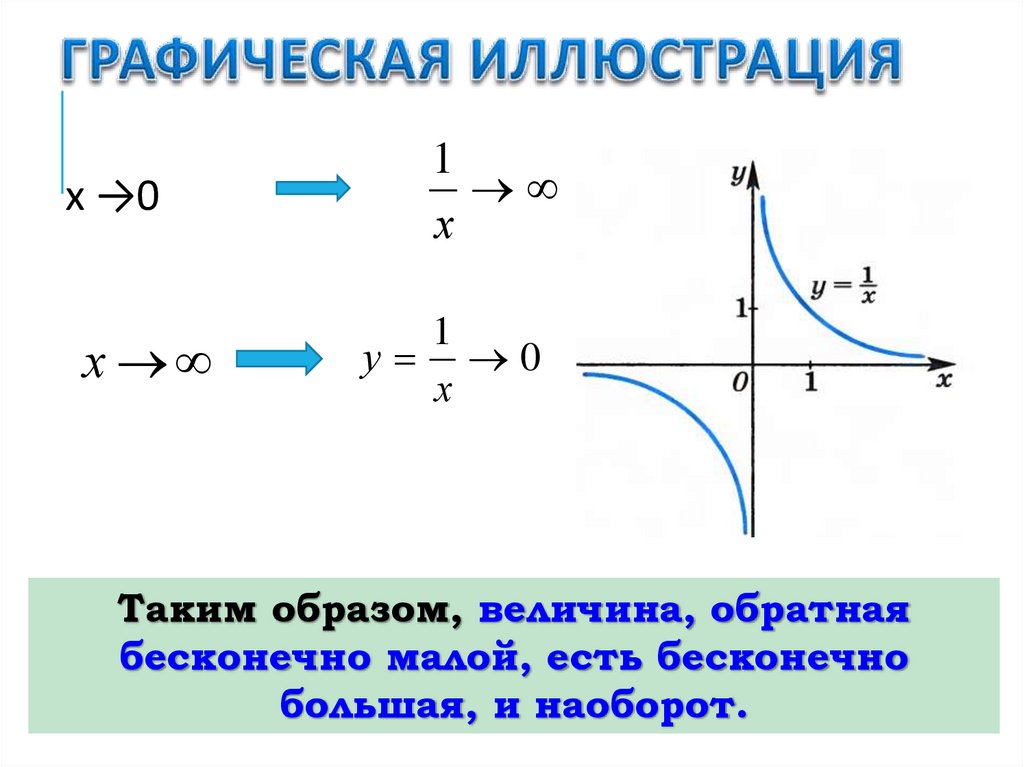
33. Графическая иллюстрация
х →0х
1
х
1
у 0
х
Таким образом, величина, обратная
бесконечно малой, есть бесконечно
большая, и наоборот.
34.
Теорема 1.lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x x0
x x0
x x0
35.
Теорема 2.lim C C
x x0
36.
Теорема 3.lim ( f ( x) g ( x)) lim f ( x) lim g ( x)
x x0
x x0
x x0
37.
Теорема 4.lim f ( x)
f ( x) x x0
lim
, если _ lim g ( x) 0
x x0 g ( x)
x x0
lim g ( x)
x x0
38.
Теорема 5.lim (k f ( x)) k lim f ( x)
x x0
x x0
39.
Теорема 6.lim ( z ) (lim z)
n
x a
x a
n
40. Основные теоремы о пределах
ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ1) lim C C , C const
2) lim f ( x) g ( x) lim f ( x) lim g ( x)
3) lim f ( x) g ( x) lim f ( x) lim g ( x)
4) lim C f ( x) C lim f ( x)
f ( x) lim f ( x)
5) lim
, lim g ( x) 0
g ( x) lim g ( x)
6) lim f ( x) lim f ( x)
n
n
41. Вычисление пределов
Вычисление предела:lim f ( x ) A
x x0
начинают с подстановки предельного значения
x0 в функцию f(x).
Если при этом получается конечное число, то предел равен этому числу.
3x 1 3 1 1 2
lim
2
2
x 1
1
x
Если при подстановки
предельного значения x0 в
функцию f(x) получаются
выражения вида:
C
0
C
0
42. Вычислить пределы:
ВЫЧИСЛИТЬПРЕДЕЛЫ:
lim ( x 2 7 x 4) 32 7 3 4 8;
x 3
x2 4
( x 2)( x 2)
x 2
lim 2
lim
lim
2;
x 2 x 2 x
x 2
x 2
x( x 2)
x
3
2( x 2)( x )
2 x 2 7 x 6 (0 / 0)
2x 3
2
lim
lim
lim
;
2
2
x 2
x 2
x 2 x 2
( x 2)
( x 2)
43.
Примеры44. Вычисление пределов
Часто при подстановке предельногозначения x0 в функцию f(x) получаются
выражения следующих видов:
0
;
0
;
Эти выражения называются
а вычисление
пределов в этом случае называется
.
45. Методы вычисления пределов на неопределенность
3x 2 x 0 0 0lim 2
x 0 2 x 5 x
0 0 0
2
0 с с
, ,
0 0
Раскрыть соответствующую неопределенность это значит найти предел (если он существует)
соответствующего выражения, что, однако не
всегда просто
46.
В большинстве случаев, чтобы раскрытьнеопределенность вида 0 , достаточно
0
числитель и знаменатель дроби
разделить на множители, и затем
сократить на множитель, приводящий к
неопределенности.
47.
ПРИМЕР №1:3x 2 x 0
lim 2
x 0 2 x 5 x
0
2
Разложим числитель и знаменатель на
множители:
x 3x 2
3x 2 2
lim
lim
x 0 x 2 x 5
x 0 2 x 5
5
48.
ПРИМЕР № 2:lim 4 x
4x
4*0
0
x 0
lim 2
2
x 0 3 x 2 x
lim 3x 2 x 3 * 0 2 * 0 0
x 0
4x
4
4
lim
lim
2.
x 0 x 3 x 2
x 0 3 x 2
3* 0 2
49.
Чтобы раскрыть неопределенность данноговида, зависящую от иррациональности,
достаточно перевести иррациональность
(или иррациональности) из числителя в
знаменатель или из знаменателя в числитель и
сократить на множитель, приводящий к
неопределенности.
50. Раскрытие неопределенностей
РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙРаскрытие неопределенности
0
0
x 2 14 x 32
0
x 2 x 16
lim
lim
2
x 2
x 2
x 6x 8
0
x 2 x 4
x 16 18
lim
9
x 2
x 4
2
Если f(x) – дробно –
рациональная
x 1 1 x 1 1
0
x 1 1 функция,
необходимо разложить
наlim
lim
Если f(x) – иррациональная
x
0
x 0
0
x
множители
числитель
и
x 1 умножить
1
дробь, x
необходимо
знаменатель дроби
числитель и знаменатель
x 1 1
1дроби на выражение,
1
lim
lim
числителю.
x 0
x 0
сопряженное
x x 1 1
x 1 1 2
51. I.Вычисление пределов функций
I.ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИЙlim 9 x 2 6 x 8
1) Вычислить
x 1
lim 9 x 2 6 x 8 lim 9 x 2 lim 6 x lim 8 9 lim x 2 6 lim x 8
x 1
x 1
x 1
x 1
x 1
x 1
9 lim x 6 lim x 8 9 12 6 1 8 9 6 8 11
2
x 1
x 1
52.
2)x 2 3x
lim
x 2 2 x 1
Вычислить
убедимся, что предел знаменателя отличен от 0:
lim 2 x 1 2 lim x lim 1 2 2 1 5
x 2
x 2
x 2
тогда применима теорема о пределе дроби:
x 3x
lim x 3 lim x 2 2 3 2 10
x 3x lim
x 2
lim
x 2
x 2
2
x 2 2 x 1
lim 2 x 1
2 lim x lim 1
2 2 1
5
2
x 2
2
2
x 2
x 2
53. II. Вычисление пределов функций. Предел знаменателя равен 0.
II. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИЙ.ПРЕДЕЛ ЗНАМЕНАТЕЛЯ РАВЕН 0.
3)
Вычислить
5
lim
x 4 3 x 12
lim 3x ⇒
12( 3х-12)
0
есть бесконечно
x 4
малая величина, а обратная ей величина есть бесконечно
большая.
5
1
lim
5 lim
5
x 4 3 x 12
x 4 3 x 12
54.
4)Вычислить
x 2 5x 6
lim
x 2 x 2 3 x 2
x 2 5x 6 0
x 3 x 2
x 3 2 3
lim
lim
lim
1
x 2 x 2 3 x 2
x
2
x
2
x 2 x 1
1 x 1 2
0
0
0
неопределённость
55.
5)Вычислить
lim
x 12
lim
x 12
lim
x 12
lim
x 12
x 4 4
x 12
x 4 4 0
lim
x 12
0 x 12
x 4 4 x 4 4
x 12 x 4 4
x 4 16
x 12
x 12 x 4 4
1
lim
1
x 12
x 12 x 4 4
1
x 4 4
12 4 4 8
56. III. Вычисление пределов функций. Предел функции при х→∞.
III. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ ФУНКЦИЙ.ПРЕДЕЛ ФУНКЦИИ ПРИ Х→∞ .
6)
Вычислить
2
lim
x 4 x 3
(4х+3) при х→∞ есть бесконечно большая величина,
а обратная ей величина есть
1
бесконечно малая.
4x 3
2
1
lim
2 lim
2 0 0
x 4 x 3
x 4 x 3
57.
7)Вычислить
x 2 5x 6
lim 2
x 2 x 6 x 8
x 2 5x 6
5 6
x
1
2
2
2
2
2
x
x
x
x 5x 6
lim
x x
lim 2
lim
x 2 x 6 x 8
x 2 2 x 2 6 x 8 x 2 6 8
x 2 2 2
2
x
x
x
x
x
2
5
6
1
1
lim 1 lim lim 2
lim 1 5 lim 6 lim 2
x
x x
x x
x
x x
x x
1 0 0 1
6
8
1
1
2 0 0 2
lim 2 lim lim 2 lim 2 6 lim 8 lim 2
x
x x
x x
x
x x
x x
58. Замечательные пределы
ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫпервый замечательный предел
sin x
lim
1;
x 0
x
второй замечательный
предел
х
1
1
lim 1 lim (1 x) x e.
x
x 0
x
59. Примеры
ПРИМЕРЫsin( 2 x)
0
lim
( )
x 0
x
0
2 sin( 2 x)
sin( 2 x)
lim
2 lim
x 0
x 0
2x
2x
2 1 2.
е
4
3
60.
Решение. Используем первый замечательный предел61.
62.
63.
64.
65.
66.
67. Односторонние пределы.
ОДНОСТОРОННИЕ ПРЕДЕЛЫ.Пределы функций при х→х0- и х→х0+
Определение «на языке последовательности»:
если f(x) стремится к пределу а при х→х0 так, что
х принимает только значения, меньшие х0, то
предел а называют пределом функции f(x) в
точке х0 слева (или левым пределом) и пишут
lim f ( x) a
x x0
68.
Определение «на языке последовательности»:если f(x) стремится к пределу а при х→х0 так, что
х принимает только значения, большие чем х0, то
предел а называют пределом функции f(x) в
точке х0 справа (или правым пределом) и пишут
lim f ( x) a
x x0
69.
1, x 0y sgn x 0, x 0
1, x 0
Пример.
у
1
0
→
lim sgn x 1
←
-1
x 0
х
lim sgn x 1
x 0
70.
Связь между односторонними пределами.Теорема. Функция f(x) имеет в точке х0 предел а
тогда и только тогда, когда в этой точке
существуют как правый так и левый пределы и
они равны. В этом случае предел функции равен
односторонним пределам:
lim f ( x) lim f ( x) lim f ( x) a
x x0
x x0
x x0
71.
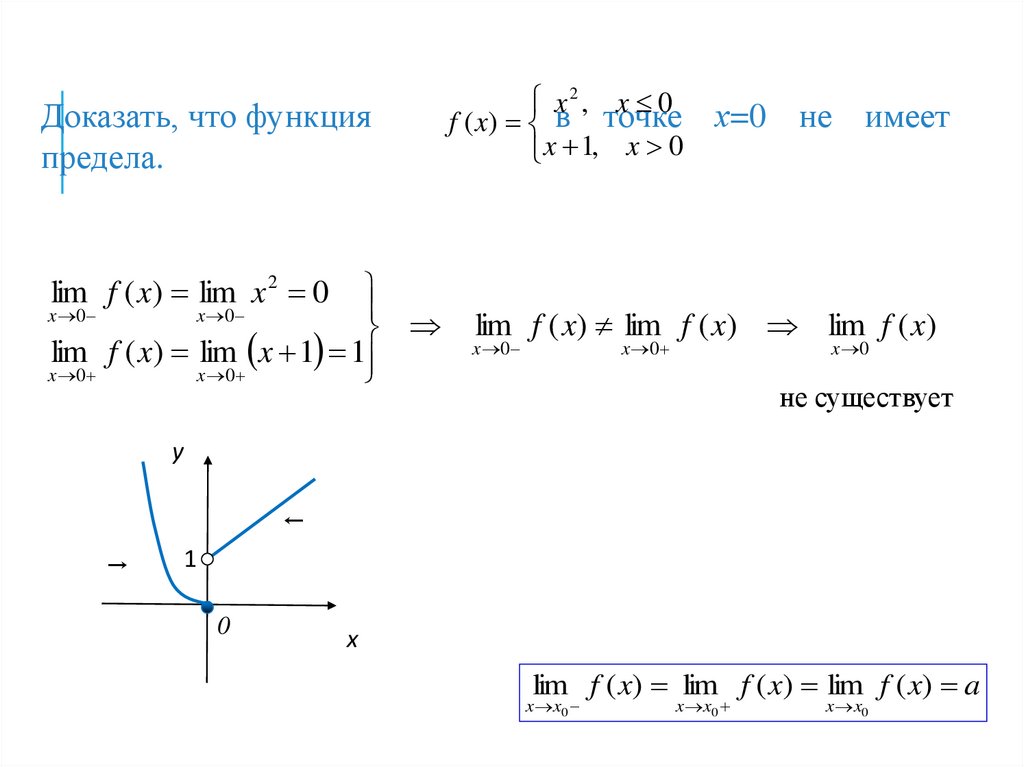
Доказать, что функцияпредела.
x 0
x 0
lim f ( x) lim x 1 1
x 0
x 0
lim f ( x) lim x 2 0
x2 , x 0
f ( x) в точке
x 1, x 0
х=0 не имеет
lim f ( x) lim f ( x) lim f ( x)
x 0
x 0
x 0
не существует
у
←
→
1
0
x
lim f ( x) lim f ( x) lim f ( x) a
x x0
x x0
x x0
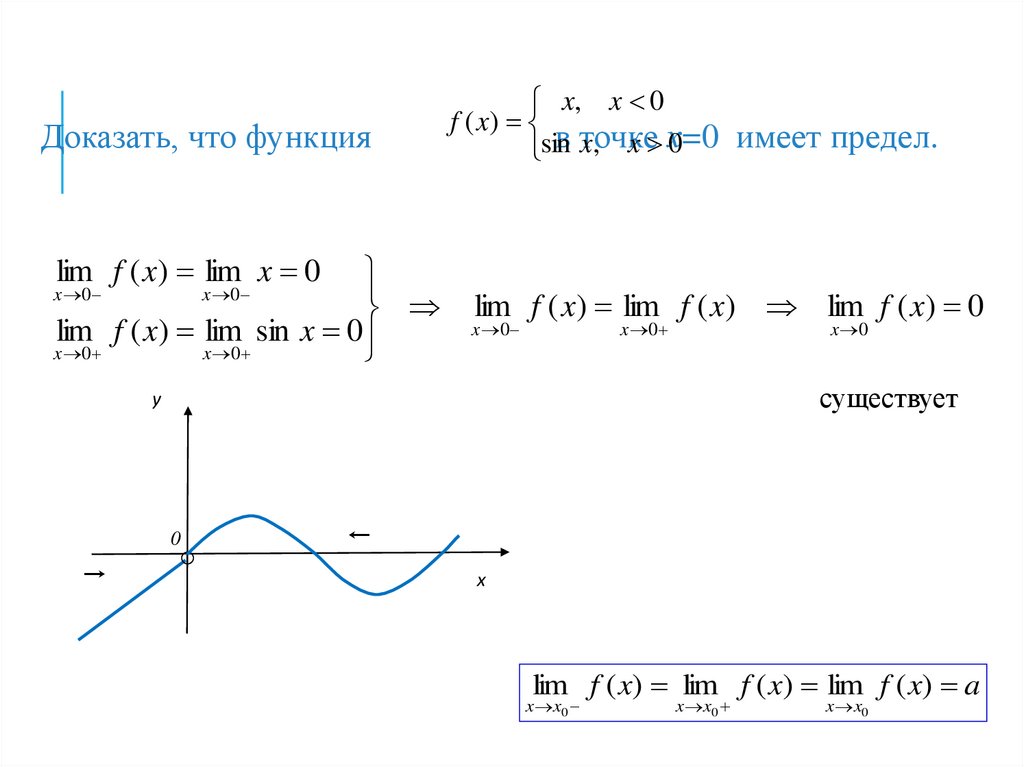
72.
Доказать, что функцияlim f ( x) lim x 0
lim f ( x) lim sin x 0
x 0
x 0
x 0
x 0
x, x 0
f ( x)
в точке
имеет предел.
x, x х=0
0
sin
lim f ( x) lim f ( x) lim f ( x) 0
x 0
x 0
x 0
существует
y
0
→
←
x
lim f ( x) lim f ( x) lim f ( x) a
x x0
x x0
x x0
73.
Пределы функций при х→∞, х→ - ∞ и х→+∞Определение «на языке последовательности»:
число а называется пределом функции f(x) при
х→∞, если для всех значений х бесконечно
большой последовательности значения функции
f(x) сколь угодно мало отличаются от а (f(x) →а) и
пишут
lim f ( x) a
x
74.
Определение «на языке последовательности»:число а называется пределом функции f(x) при
х→+∞ (х→-∞), если для всех значений х
бесконечно
большой
последовательности,
элементы
которой
положительны
(отрицательны), значения функции f(x) сколь
угодно мало отличаются от числа а (f(x) →а)
и пишут
lim f ( x) a
x
( lim f ( x) a )
x
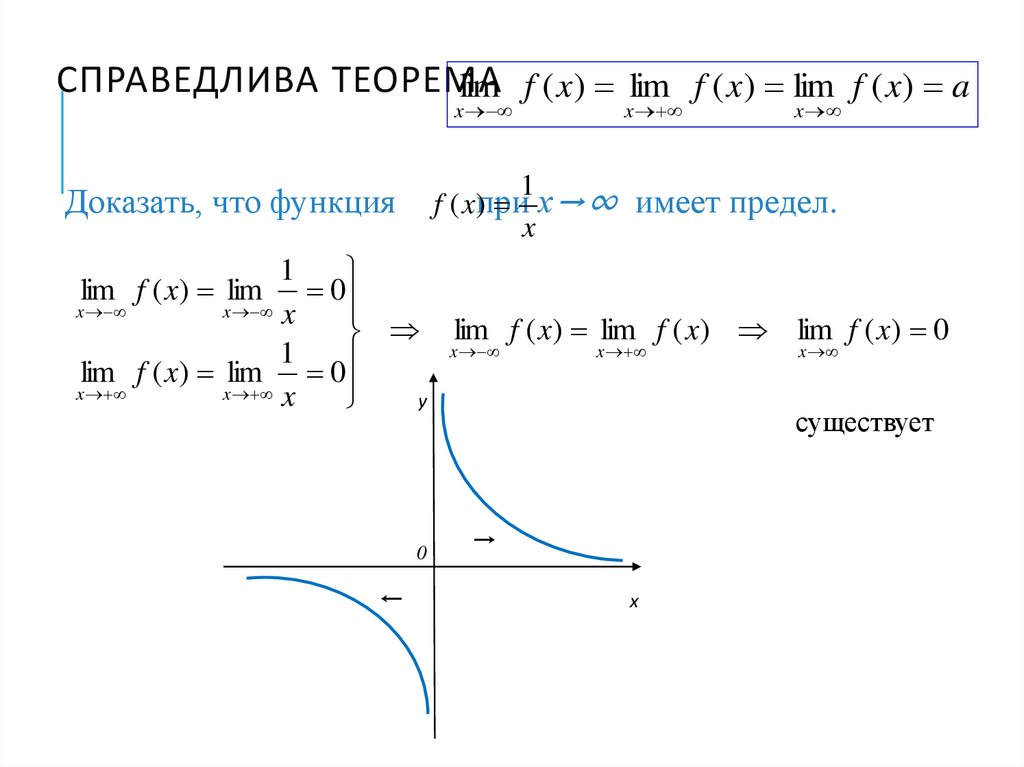
75. Справедлива теорема
СПРАВЕДЛИВА ТЕОРЕМАlim f ( x) lim f ( x) lim f ( x) a
x
x
x
1
f ( xпри
) х→∞ имеет предел.
x
Доказать, что функция
1
0
x
x x
f ( x) lim f ( x) lim f ( x) 0
xlim
x
x
1
lim f ( x) lim 0
x
x x
у
lim f ( x) lim
существует
0
←
→
x
76. Бесконечно малые и бесконечно большие функции.
БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНОБОЛЬШИЕ ФУНКЦИИ.
Функция α=α(х) называется бесконечно малой функцией (или просто бесконечно малой) в точке х0 (или при х→х0), если
lim ( x) 0
x x0
Аналогично определяются бесконечно малые функции при х→х0- , х→х0+,
х→-∞, х→+∞, х→∞.
Бесконечно малые функции обладают такими же свойствами,
что и бесконечно малая переменная величина.
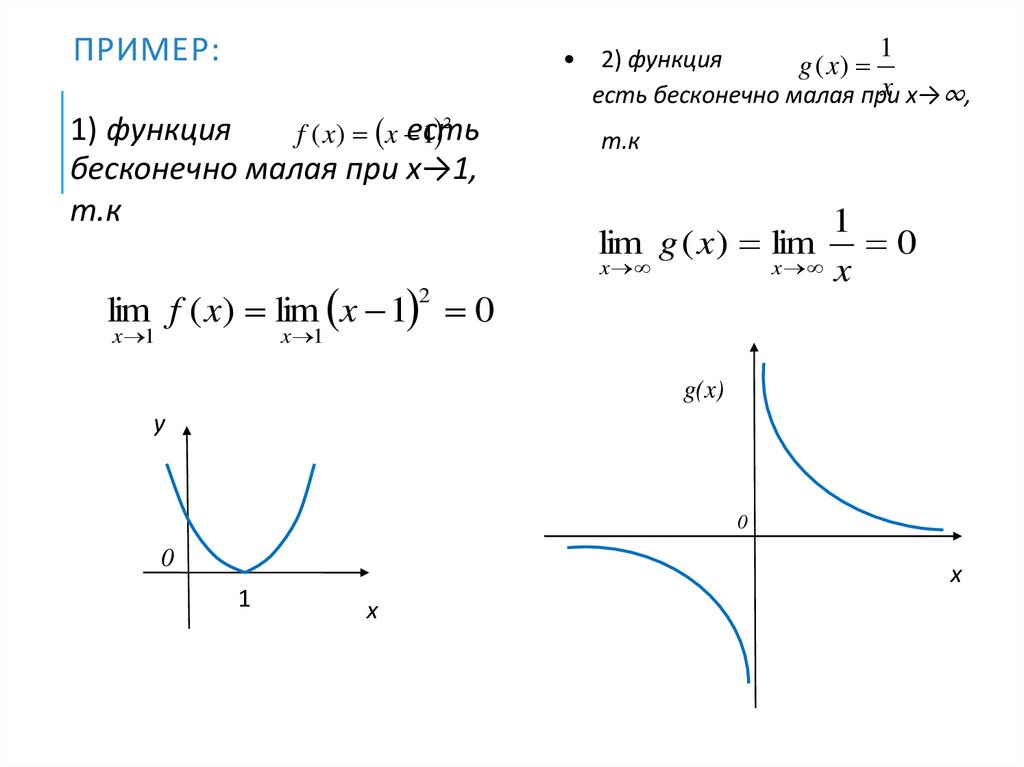
77. Пример:
ПРИМЕР:2
1) функция
f ( x) x есть
1
бесконечно малая при х→1,
т.к
lim f ( x) lim x 1 0
2
x 1
1
2) функция
g ( x)
x х→∞,
есть бесконечно малая при
т.к
1
lim g ( x ) lim 0
x
x x
x 1
g(x)
y
0
0
1
x
x
78.
Функция f(x) называется бесконечно большой функцией (или просто бесконечно большой) в точке х=х0 (или при х→х0), еслиlim f ( x)
x x0
Аналогично определяются бесконечно большие функции при
х→х0- , х→х0+, х→-∞, х→+∞, х→∞.
Если f(x) стремится к бесконечности при х→х0 и при этом
принимает
только
положительные
или
только
отрицательные значения, соответственно пишут
lim f ( x)
x x0
lim f ( x)
x x0
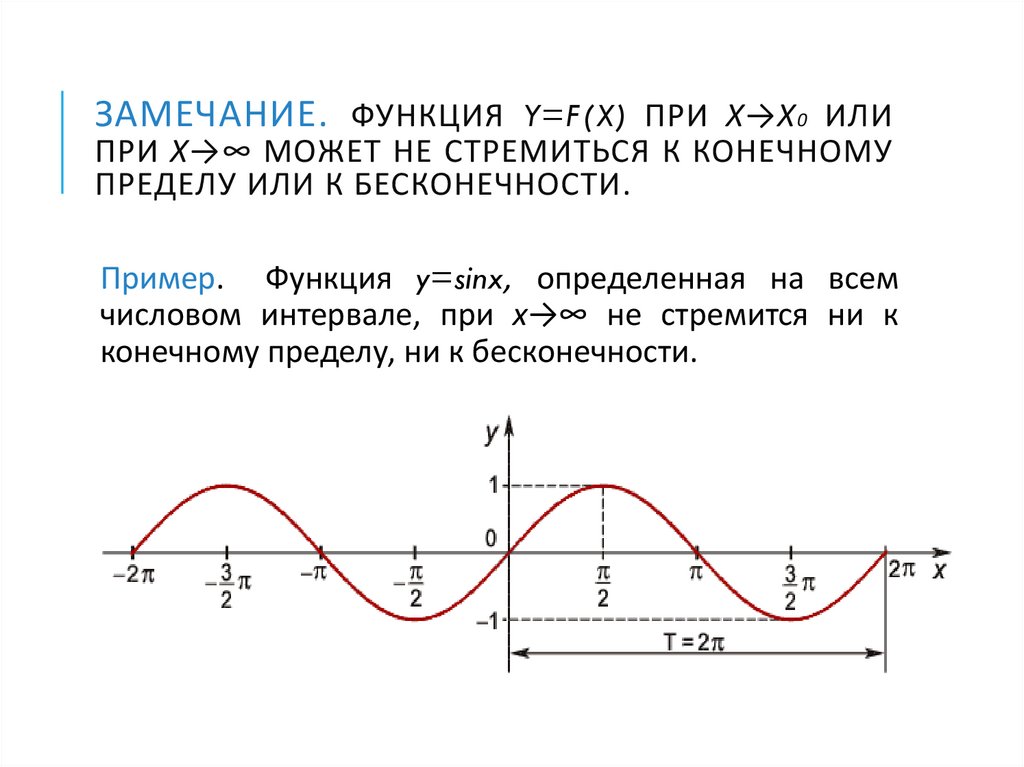
79. Замечание. Функция y=f(x) при х→х0 или при х→∞ может не стремиться к конечному пределу или к бесконечности.
ЗАМЕЧАНИЕ. ФУНКЦИЯ Y=F(X) ПРИ Х→Х 0 ИЛИПРИ Х→∞ МОЖЕТ НЕ СТРЕМИТЬСЯ К КОНЕЧНОМУ
ПРЕДЕЛУ ИЛИ К БЕСКОНЕЧНОСТИ.
Пример. Функция y=sinx, определенная на всем
числовом интервале, при х→∞ не стремится ни к
конечному пределу, ни к бесконечности.




















































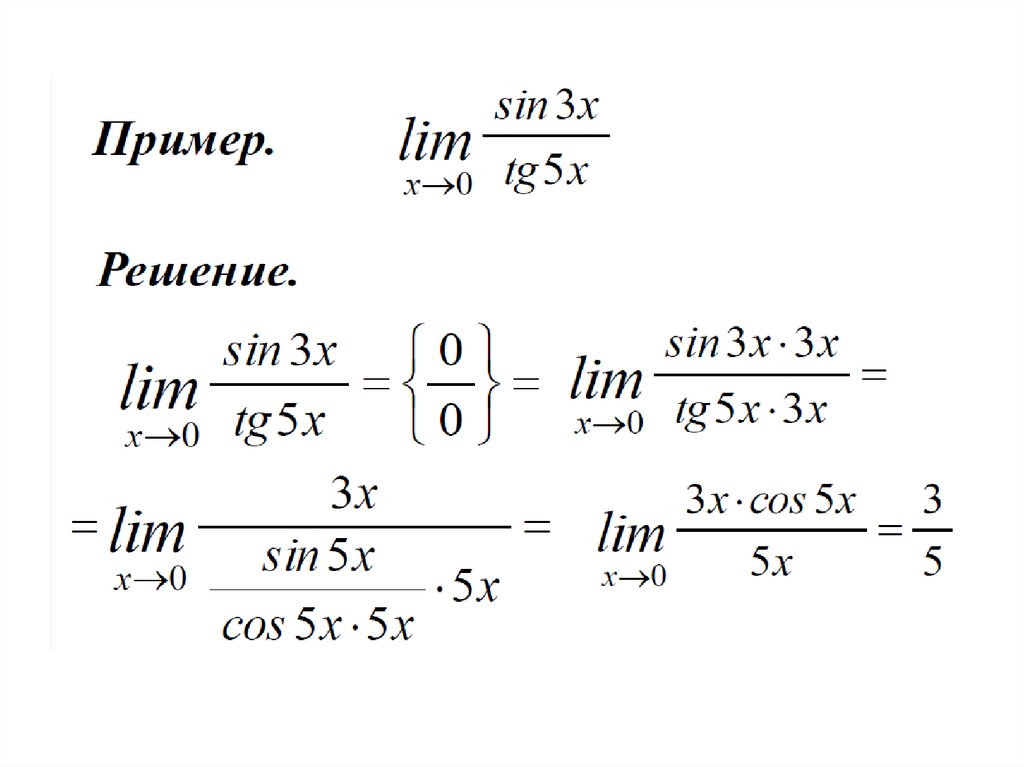

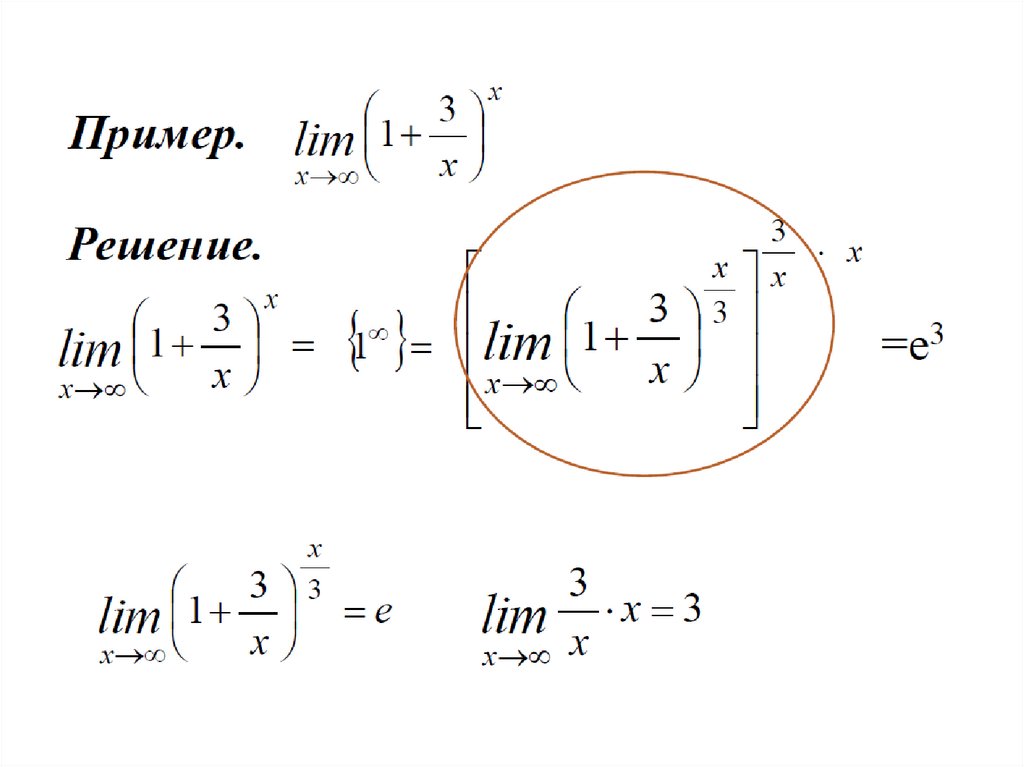











 mathematics
mathematics








