1.06M

Category: $mathematics$ mathematics

Предел и непрерывность функции

Бесконечно малая и бесконечно большие
величины.
• Переменная величина α называется бесконечно малой, если
она изменяется так, что какое бы малое положительное число
ℰ ни взято , ∣α∣ становится и при дальнейшем изменении
величины α остается меньше ℰ.
α→0
1
1
1
1
: 1; ; ; ; ;...
2
3
4
5
-1
0
или
: 1;
1
1 1
;
;
2 3
1 1
;
;...
4 5

3.

• Переменная величина у называется бесконечно большой,
если она изменяется так, что какое бы большое
положительное число N ни взято , ∣у∣ становится и при
дальнейшем изменении величины у остается больше N.
у→∞
или
y : 2; 4; 6; 8; ...
0
y : 2; 4; 6; 8; ...

4.

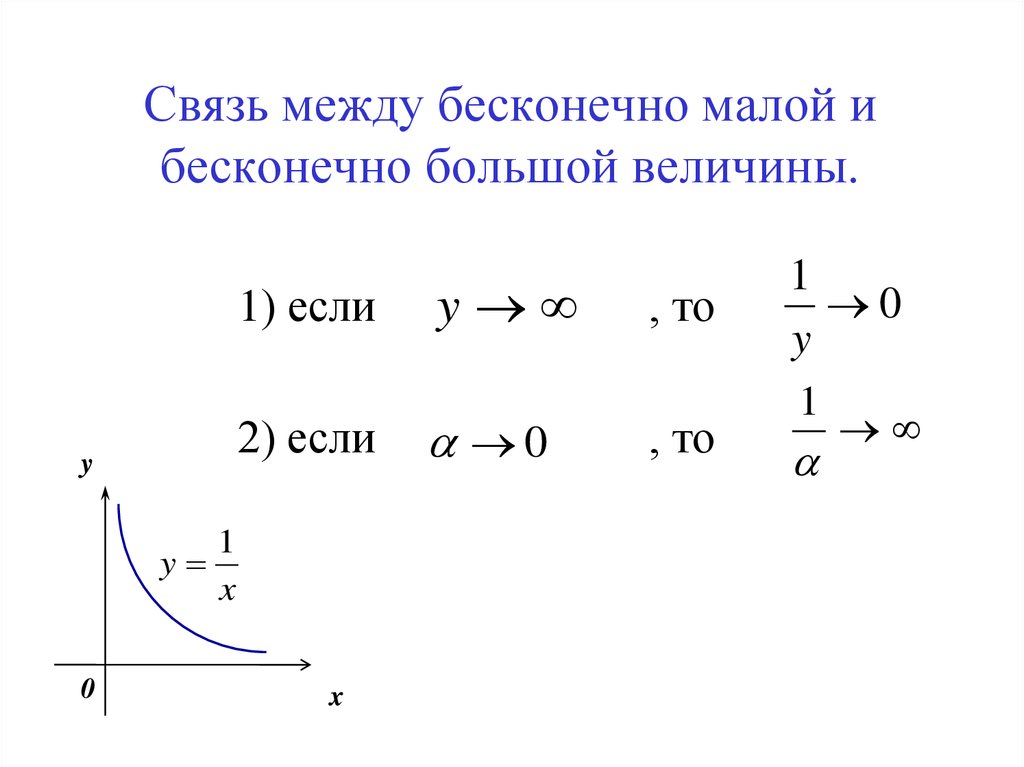
Связь между бесконечно малой и
бесконечно большой величины.
1) если
2) если
y
y
0
1
x
x
y
0
, то
, то
1
0
y
1

5.

пример:
1) y : 1, 10, 100, 1000, ... , тогда
1
: 1 0,1 0,01 0,001 ... 0
y
2) : 1 0,1 0,01 0,001 ... 0 , тогда
1
: 1, 10, 100, 1000, ...

6.

Предел переменной
x : 3,1 3,01 3,001 3,0001 ... 3
x 3 : 0,1 0,01 0,001 0,0001 ... 0
Число 3 называется пределом переменной х:
lim x 3
или
x 3

7.

• Постоянная а называется пределом переменной
х, если разность между ними есть бесконечно
малая величина α, т.е
lim x a
, если
x a
lim 0
lim y
или
x a 0

8.

Предел функции
y x 4
2
x : 3,1 3,01 3,001 3,0001 ... 3
y : 5,6 5,06 5,006 5,0006 ... 5
lim x2 4 5
x 3

9.

• Определение «на языке последовательности»
Число а называется пределом функции f(x) в
точке х=х0, если для всех значений х,
достаточно близких к х0 (х→х0) и отличных от
х0 (х≠х0), значение функции f(x) сколь угодно
мало отличается от числа а (f(x)→а), т.е
lim f ( x) a
x x0
или
f ( x) a
при
x x0

10.

Односторонние пределы.
Пределы функций при х→х0- и х→х0+
Определение «на языке последовательности»:
если f(x) стремится к пределу а при х→х0 так, что
х принимает только значения, меньшие х0, то
предел а называют пределом функции f(x) в
точке х0 слева (или левым пределом) и пишут
lim f ( x) a
x x0

11.

Определение «на языке последовательности»:
если f(x) стремится к пределу а при х→х0 так, что
х принимает только значения, большие чем х0, то
предел а называют пределом функции f(x) в
точке х0 справа (или правым пределом) и пишут
lim f ( x) a
x x0

12.

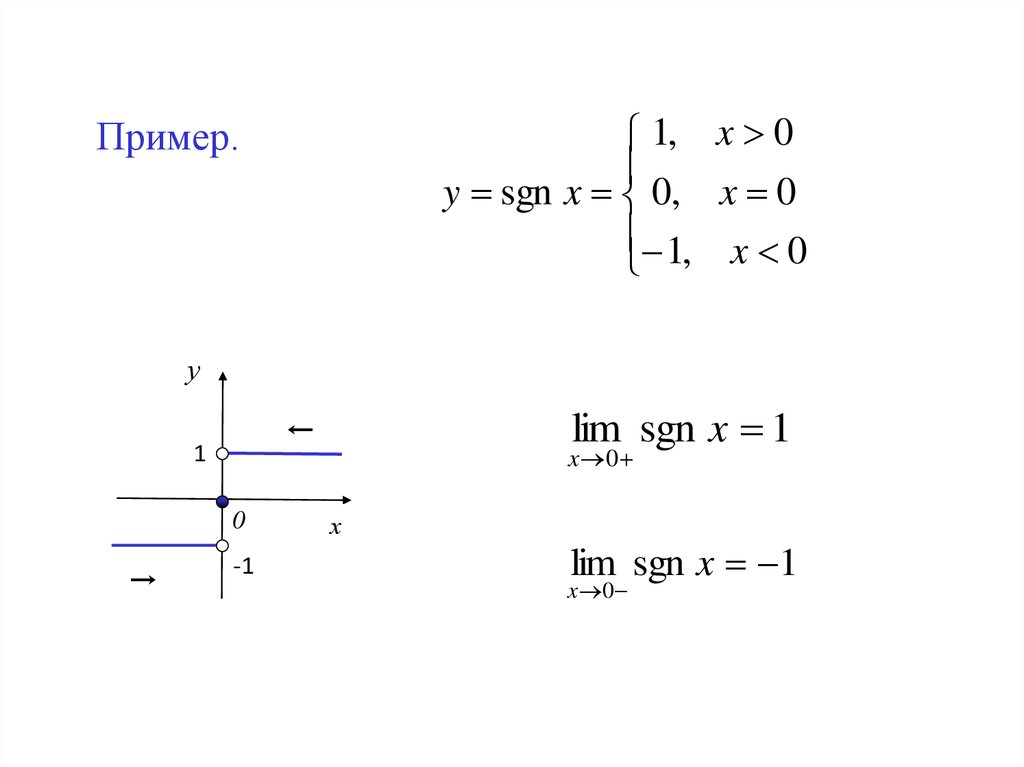
1, x 0
y sgn x 0, x 0
1, x 0
Пример.
у
1
0
→
lim sgn x 1
←
-1
x 0
х
lim sgn x 1
x 0

13.

Связь между односторонними пределами.
Теорема. Функция f(x) имеет в точке х0 предел а
тогда и только тогда, когда в этой точке
существуют как правый так и левый пределы и
они равны. В этом случае предел функции равен
односторонним пределам:
lim f ( x) lim f ( x) lim f ( x) a
x x0
x x0
x x0

14.

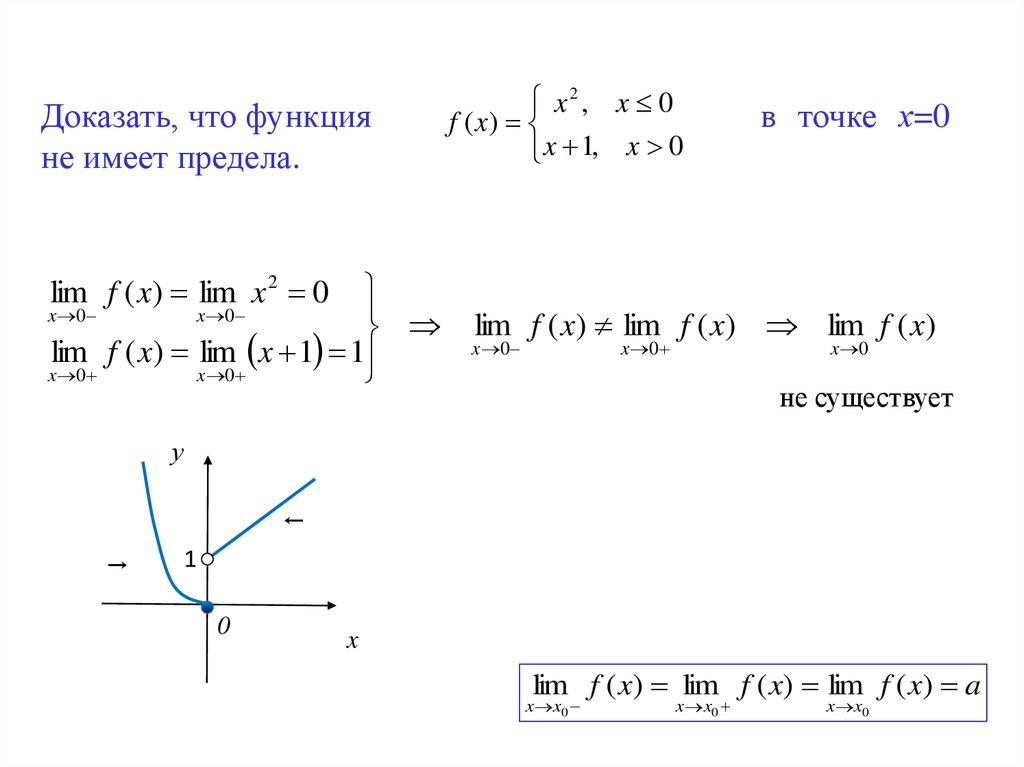
Доказать, что функция
не имеет предела.
x 0
x 0
lim f ( x) lim x 1 1
x 0
x 0
lim f ( x) lim x 2 0
x2 , x 0
f ( x)
x 1, x 0
в точке х=0
lim f ( x) lim f ( x) lim f ( x)
x 0
x 0
x 0
не существует
у
←
→
1
0
x
lim f ( x) lim f ( x) lim f ( x) a
x x0
x x0
x x0

15.

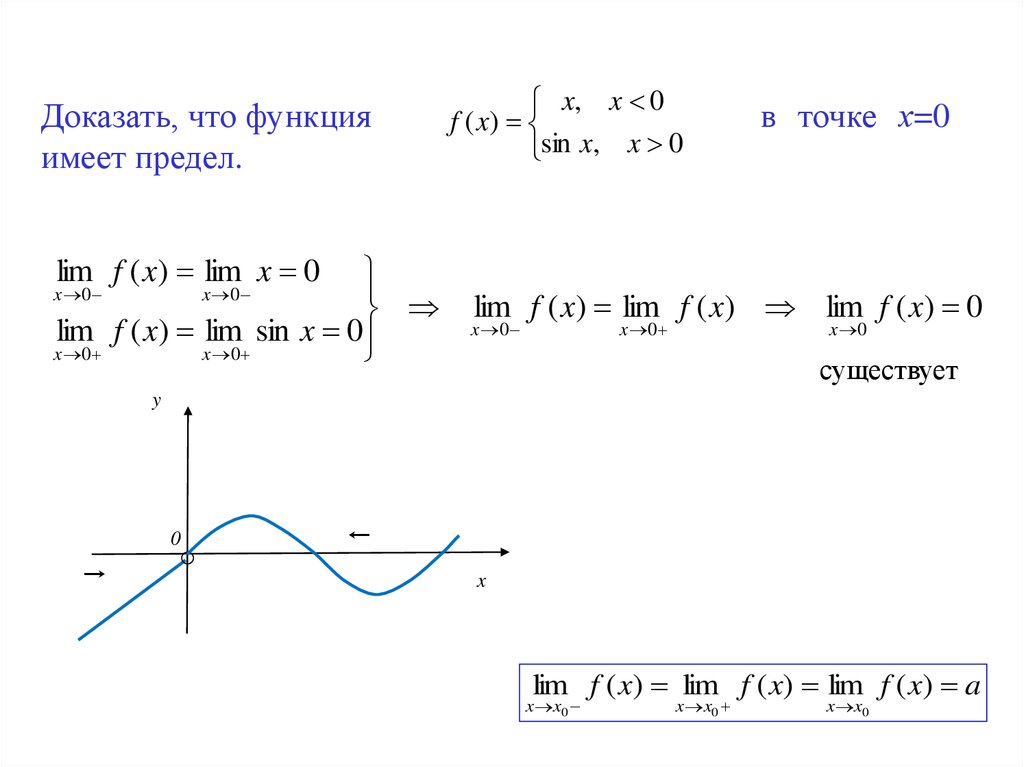
Доказать, что функция
имеет предел.
lim f ( x) lim x 0
lim f ( x) lim sin x 0
x 0
x 0
x 0
x 0
x, x 0
f ( x)
sin x, x 0
в точке х=0
lim f ( x) lim f ( x) lim f ( x) 0
x 0
x 0
x 0
существует
y
0
→
←
x
lim f ( x) lim f ( x) lim f ( x) a
x x0
x x0
x x0

16.

Пределы функций при х→∞, х→ - ∞ и х→+∞
Определение «на языке последовательности»:
число а называется пределом функции f(x) при
х→∞, если для всех значений х бесконечно
большой последовательности значения функции
f(x) сколь угодно мало отличаются от а (f(x) →а)
и пишут
lim f ( x) a
x

17.

Определение «на языке последовательности»:
число а называется пределом функции f(x) при
х→+∞ (х→-∞), если для всех значений х
бесконечно
большой
последовательности,
элементы
которой
положительны
(отрицательны), значения функции f(x) сколь
угодно мало отличаются от числа а (f(x) →а)
и пишут
lim f ( x) a
x
( lim f ( x) a )
x

18.

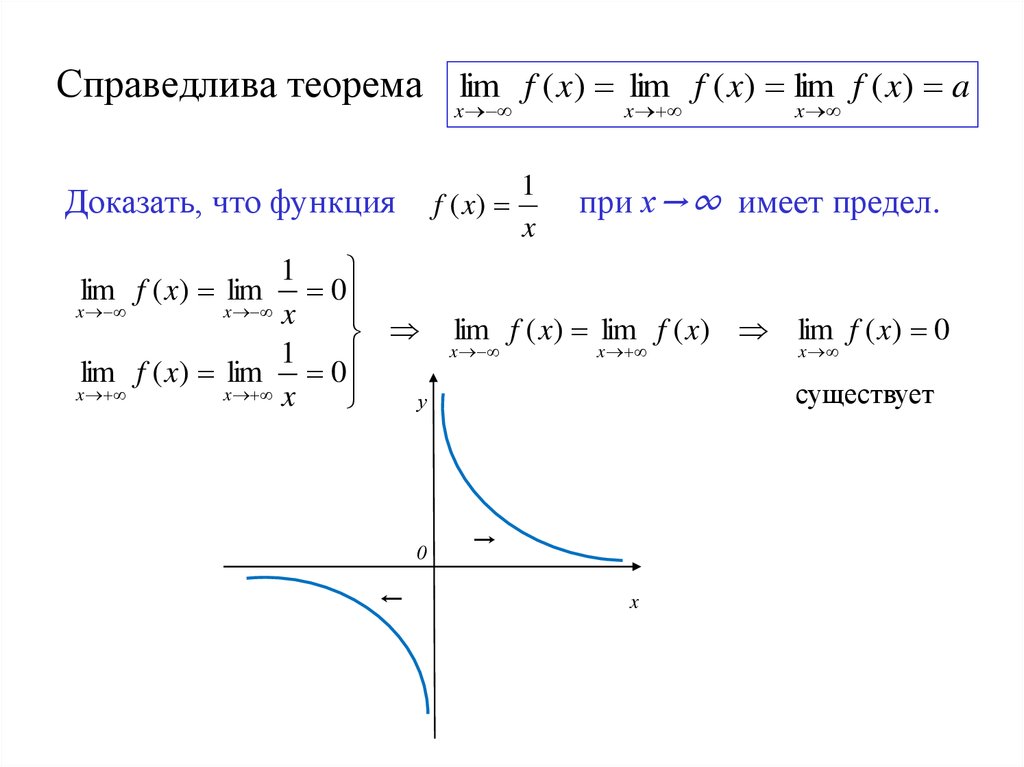
Справедлива теорема lim f ( x) lim f ( x) lim f ( x) a
x
Доказать, что функция
f ( x)
x
1
x
x
при х→∞ имеет предел.
1
0
x
x x
f ( x) lim f ( x) lim f ( x) 0
xlim
x
x
1
lim f ( x) lim 0
x
x x
существует
у
lim f ( x) lim
0
←
→
x

19.

Бесконечно малые и бесконечно большие
функции.
• Функция α=α(х) называется бесконечно малой
функцией (или просто бесконечно малой) в точке х0 (или
при х→х0), если
lim ( x) 0
x x0
Аналогично определяются бесконечно малые функции
при х→х0- , х→х0+, х→-∞, х→+∞, х→∞.
Бесконечно малые функции обладают такими же свойствами, что
и бесконечно малая переменная величина.

20.

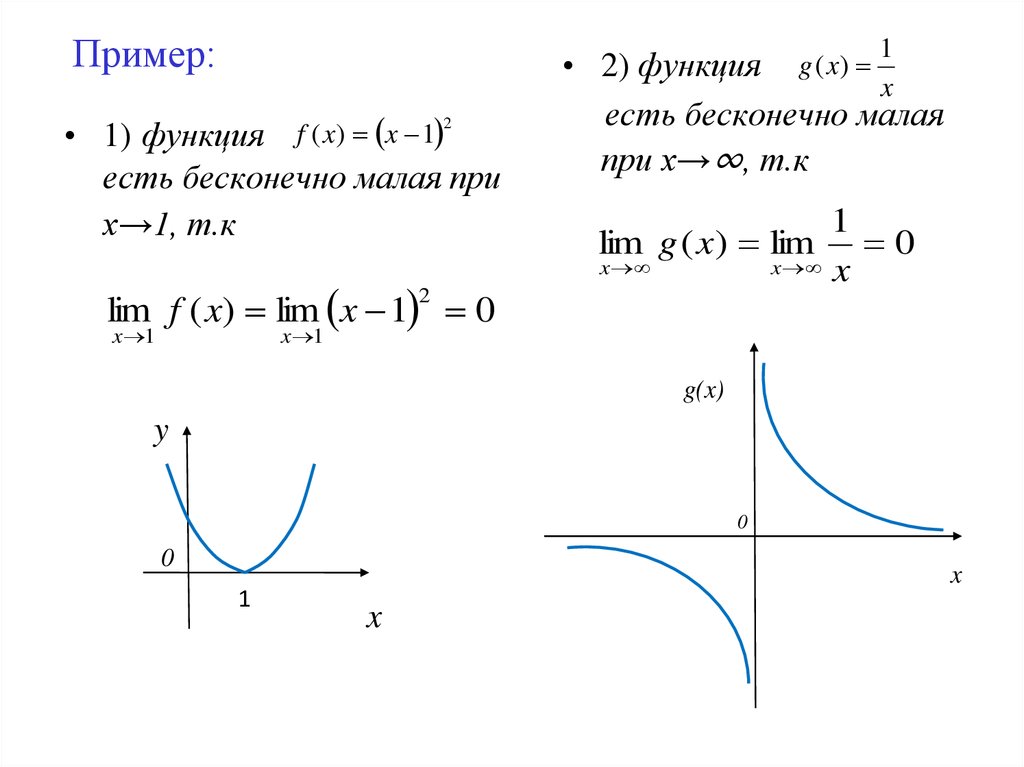
Пример:
1
• 1) функция f ( x) x 1
есть бесконечно малая при
х→1, т.к
2
lim f ( x) lim x 1 0
2
x 1
• 2) функция g ( x)
x
есть бесконечно малая
при х→∞, т.к
1
lim g ( x) lim 0
x
x x
x 1
g(x)
y
0
0
1
x
x

21.

• Функция f(x) называется бесконечно большой
функцией (или просто бесконечно большой) в точке
х=х0 (или при х→х0), если
lim f ( x)
x x0
Аналогично определяются бесконечно большие функции при
х→х0- , х→х0+, х→-∞, х→+∞, х→∞.
Если f(x) стремится к бесконечности при х→х0 и при этом
принимает только положительные или только отрицательные
значения, соответственно пишут
lim f ( x)
x x0
lim f ( x)
x x0

22.

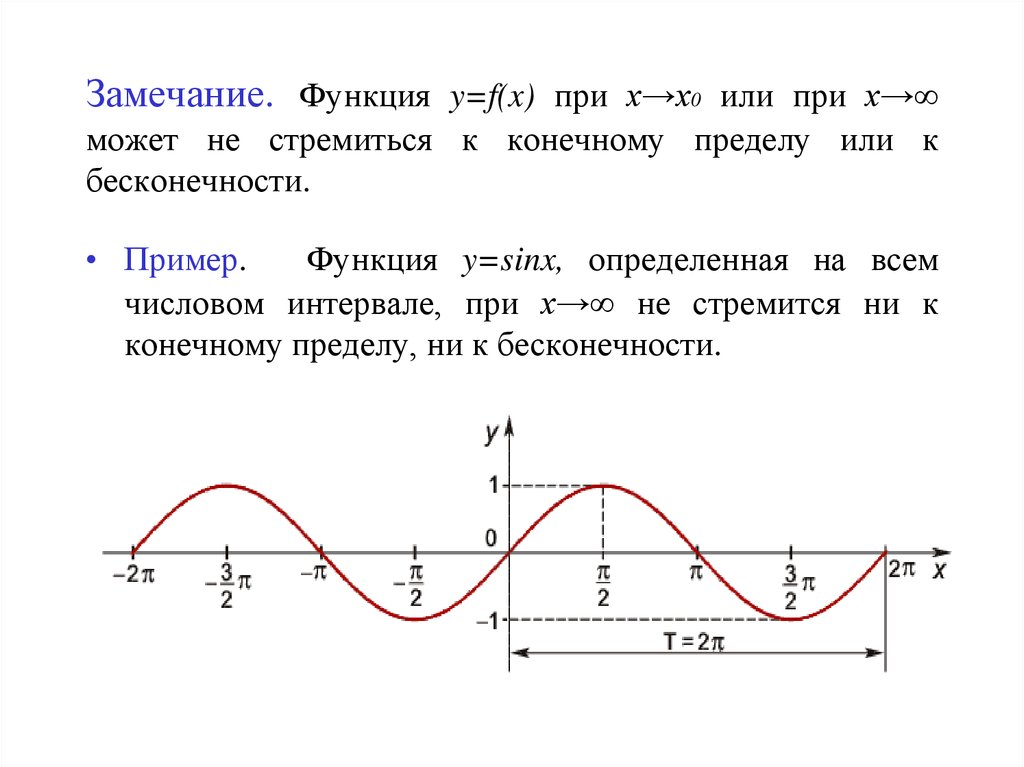
Замечание. Функция y=f(x) при х→х0 или при х→∞
может не стремиться к конечному пределу или к
бесконечности.
• Пример.
Функция y=sinx, определенная на всем
числовом интервале, при х→∞ не стремится ни к
конечному пределу, ни к бесконечности.

23.

Основные теоремы о пределах
1) lim C C , C const
2) lim f ( x) g ( x) lim f ( x) lim g ( x)
3) lim f ( x) g ( x) lim f ( x) lim g ( x)
4) lim C f ( x) C lim f ( x)
f ( x) lim f ( x)
5) lim
, lim g ( x) 0
g ( x) lim g ( x)
6) lim f ( x) lim f ( x)
n
n

24.

Основные теоремы о пределах
7) Пусть функции f(x), g(x) и h(x) определены в
некоторой окрестности точки х0, за исключением
может быть самой точки х0, и функции f(x) и h(x)
имеют в точке х0 предел, равный а, т.е.
lim f ( x) lim h( x) a
x x0
x x0
Пусть, кроме того, выполняется неравенство:
f ( x ) g ( x ) h( x )
Тогда
lim g ( x) a
x x0

25.

I.Вычисление пределов функций.
lim 9 x 2 6 x 8
1) Вычислить
x 1
lim 9 x 2 6 x 8 lim 9 x 2 lim 6 x lim 8 9 lim x 2 6 lim x 8
x 1
x 1
x 1
x 1
x 1
x 1
9 lim x 6 lim x 8 9 12 6 1 8 9 6 8 11
2
x 1
x 1

26.

x 2 3x
lim
x 2 2 x 1
Вычислить
2)
убедимся, что предел знаменателя отличен от 0:
lim 2 x 1 2 lim x lim 1 2 2 1 5
x 2
x 2
x 2
тогда применима теорема о пределе дроби:
x 3x
lim x 3 lim x 2 2 3 2 10
x 3x lim
x 2
lim
x 2
x 2
2
x 2 2 x 1
lim 2 x 1
2 lim x lim 1
2 2 1
5
2
x 2
2
2
x 2
x 2

27.

II. Вычисление пределов функций.
Предел знаменателя равен 0.
3)
Вычислить
lim 3x 12 0
x 4
5
lim
x 4 3 x 12
⇒
(3х-12) есть бесконечно
малая величина, а обратная ей величина есть
бесконечно большая.
5
1
lim
5 lim
5
x 4 3 x 12
x 4 3 x 12

28.

4) Вычислить
x 2 5x 6
lim
x 2 x 2 3 x 2
x 2 5x 6 0
x 3 x 2
x 3 2 3
lim
lim
lim
1
x 2 x 2 3 x 2
x
2
x
2
x 2 x 1
1 x 1 2
0
0
0
неопределённость

29.

5) Вычислить
lim
x 12
lim
x 12
lim
x 12
lim
x 12
x 4 4
x 12
x 4 4 0
lim
x 12
0 x 12
x 4 16
x 12
1
x 4 4
x 4 4
x 12
lim
1
x 12
x 4 4
x 12
x 12
1
x 4 4
12 4 4 8
x 4 4
x 4 4

30.

III. Вычисление пределов функций.
Предел функции при х→∞.
6)
Вычислить
2
lim
x 4 x 3
(4х+3) при х→∞ есть бесконечно большая величина,
а обратная ей величина есть
малая.
1
4x 3
бесконечно
2
1
lim
2 lim
2 0 0
x 4 x 3
x 4 x 3

31.

7) Вычислить
x 2 5x 6
lim 2
x 2 x 6 x 8
x 2 5x 6
5 6
x
1
2
2
2
2
2
x
x
x
x 5x 6
lim
x x
lim
lim
x 2 x 2 6 x 8
x 2 2 x 2 6 x 8 x 2 6 8
x 2 2 2
2
x
x
x
x
x
2
5
6
1
1
lim 1 lim lim 2
lim 1 5 lim 6 lim 2
x
x x
x x
x
x x
x x
1 0 0 1
6
8
1
1
2 0 0 2
lim 2 lim lim 2 lim 2 6 lim 8 lim 2
x
x x
x x
x
x x
x x

32.

Для раскрытия неопределенности вида
числитель и знаменатель дроби надо делить на
старшую степень х.

English Русский Rules