Предел функции. Лекция №8

1.

Лекция № 8. Предел функции
Учебные вопросы:
1. Предел функции в точке и на
бесконечности.
2. Основные свойства предела функции.
3. Бесконечно малые функции и их
свойства.

2.

В1. Предел функции в точке и на
бесконечности
Рассмотрим
функцию
у=f(x),
определенную на множестве Х и точку х0,
быть может, и не принадлежащую
множеству Х, но обладающей тем
свойством, что в любой её окрестности
есть точки множества Х.

3.

Определение 1. (по Гейне)
Число А называется пределом функции
y=f(x) в точке х0, если для любой
последовательности {xn} сходящейся к х0
xn X и xn x0 , соответствующая
последовательность значений функции
{ f(xn) } сходится к числу А.

4.

Определение 2. (по Коши)
Число А называется пределом функции
f(x) в точке х0, если для каждого > 0
можно указать такое число > 0, что
для всех хϵX и х≠х0 и удовлетворяющих
неравенству |x–х0| , имеет место
неравенство |f(x)–A| .
Обозначение lim f ( x) A или
x x0
f(x) А при х х0

5.

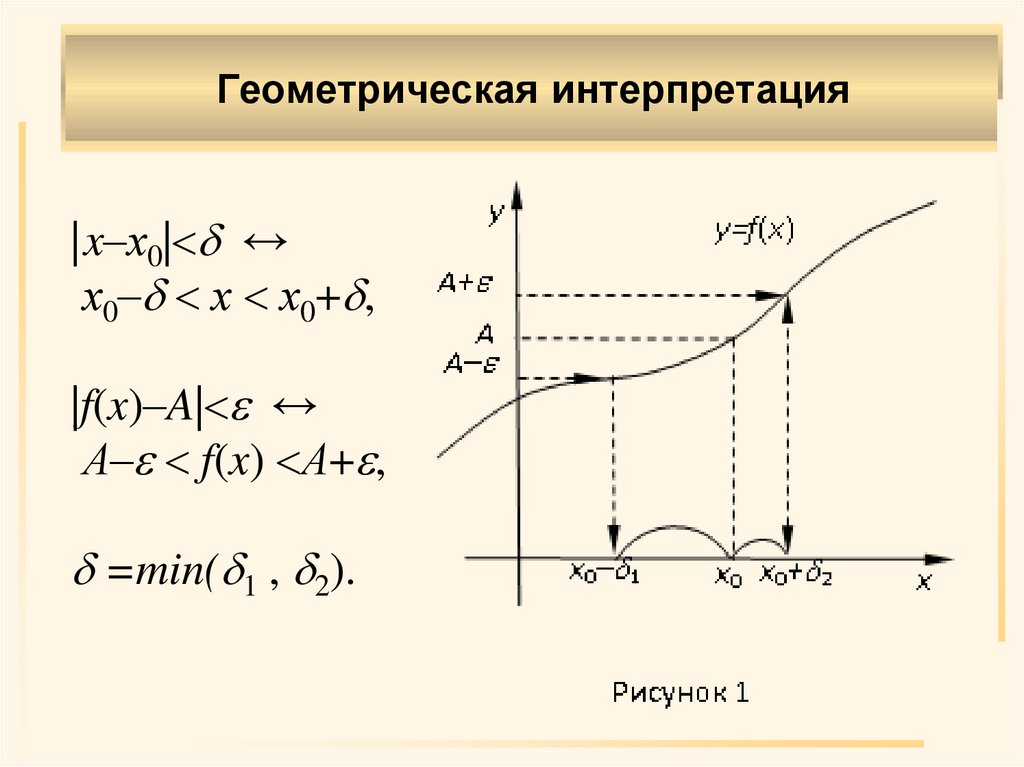
Геометрическая интерпретация
|x–х0| ↔
х0– х х0+ ,
|f(x)–A| ↔
А– f(x) А+ ,
=min( 1 , 2).

6.

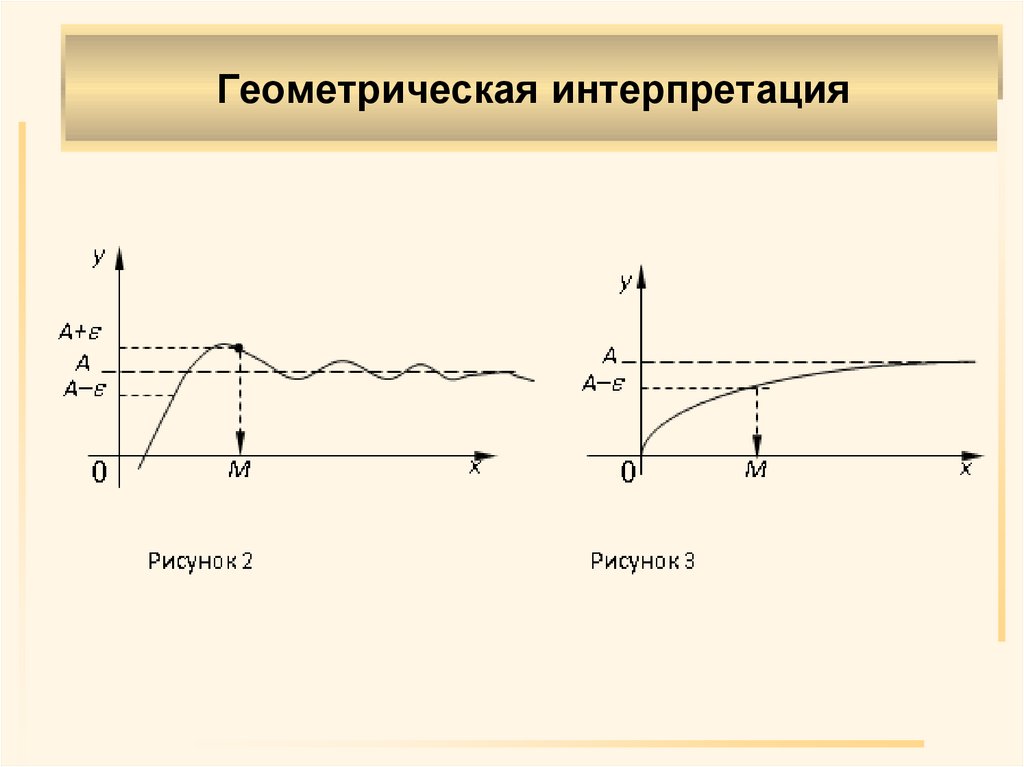
Предположим, что f(x) определена при сколь угодно
больших значениях x, то есть Х= D(f ) неограниченна.
Определение 3. (по Гейне). Число А
называется пределом функции f(x) на
бесконечности, то есть при
x x , если xn xn ,
соответствующая последовательность
Обозначают:
f ( xn ) A.
lim f ( x) A или f ( x) A , при х
x
( lim f ( x) A или f ( x) A , при х ).
x

7.

Определение 4. (по Коши)
Число А
называется пределом
функции f(x) на бесконечности, то есть
x x ,
при
если >0, M 0 такое, что
x M ( x M )
выполняется условие
f ( x) A .

8.

Геометрическая интерпретация

9.

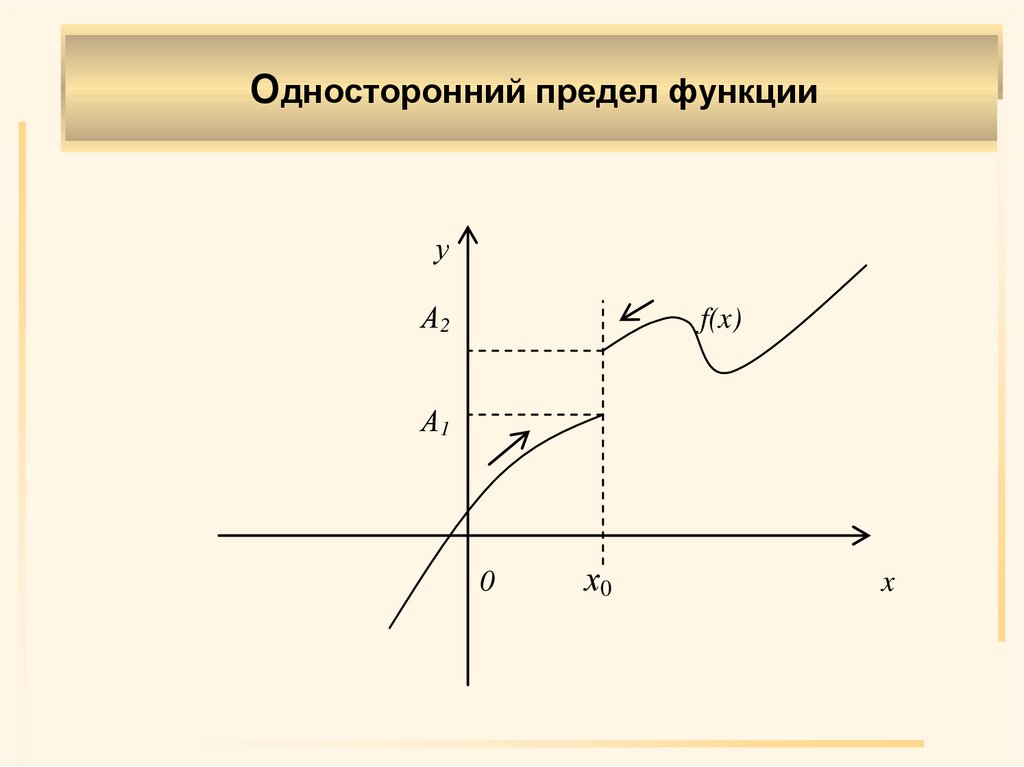
Односторонние пределы
Определение 5. Если f(x) A1 при х х0
только при x < х0, то
lim f ( x ) A1
x х0 0
- называется пределом функции f(x) в
точке х = х0 слева,
а если f(x) A2 при х х0 только при
lim f ( x ) A2
x > х0, то
x х0 0
называется пределом функции f(x) в
точке х = х0 справа.

10.

Определение 6.
Число A1 (A2) называется правым
(левым) пределом функции f(x) в точке х0,
если 0, 0 такое, что х Х и
удовлетворяющих условиям |x–х0| и
х>x0 (x<x0) выполняется неравенство
|f(x)–А| .

11.

Обозначения односторонних пределов
Обозначение предела справа
f(x0+0) или lim f ( x) ,
x x0 0
Обозначение предела слева
f(x0–0) или lim f ( x) .
x x0 0

12.

Односторонний предел функции
у
А2
f(x)
А1
0
х0
x

13.

2. Основные свойства предела функции
Свойство 1. (Единственность предела). Если
lim f ( x) A и
x x0
lim f ( x) B,
x x0
то А=В.
Свойство 2. Если существует lim f ( x), то
x x0
f(х) ограничена в некоторой окрестности х0.

14.

Свойство 3.
Если f(x) монотонна и ограничена
некоторой окрестности точки
х = х0 , то существует
lim f ( x) .
x x0
в

15.

Свойство 4.
Если функции f(x) и g(x) имеют в точке х0
конечные пределы А и В, то
1) lim С С ;
x x0
2) lim Cf ( x) С lim f ( x) ;
x x0
x x0
3) lim f ( x) g ( x) A B ;
x x0
4) lim f ( x) g ( x) A B ;
x x0
f ( x) A
5) lim
, B 0 .
x x 0 g ( x)
B

16.

Свойство 5.
Если в окрестности точки х0, (исключая быть
может саму точку х0), выполняется условие
f(x) (x) g(x) и
lim f ( х) lim g ( х) А ,
x x0
x x0
то функция (x) также имеет предел в точке
х0 и
lim ( х) А .
x x0

17.

Свойство 6.
Если в окрестности точки х0, (исключая быть
может саму точку х0), выполняется условие
f(x) g(x) и
lim f ( x ) A , lim g ( x ) B ,
x
то А В.
x

18.

3. Бесконечно малые функции и их свойства
Определение 7. Функция f(x) называется
бесконечно малой в точке x0, если
lim f ( x) 0 .
x x0
Обозначают (х), (х).

19.

Определение 8.
Если
( x)
lim
0 , где (х) и (х)
x a ( x)
– бесконечно малые величины при х а,
то
функция
(х)
называется
бесконечно малой более высокого
порядка, чем функция (х).

20.

Определение 9.
Если
( x)
lim
A, A 0, A const ,
x x0 ( x)
то (х) и (х) называются бесконечно
малыми одного порядка.

21.

Определение 10.
( x)
1, то функции (х) и
Если lim
x x0 ( x)
(х)
называются эквивалентными
бесконечно малыми.
Записывают (х) ~ (х).
Пример. Сравнить бесконечно малые
функции f(x)=x10 и f(x)=x при х 0.

22.

Определение 11.
Бесконечно
малая
функция
(х)
называется бесконечно малой порядка k
относительно бесконечно малой
( x)
функции (х), если предел xlim
x0 ( x) k
конечен и отличен от нуля.

23.

Свойства бесконечно малых функций
Свойство 1. Сумма конечного числа
бесконечно малых функций при х х0
тоже бесконечно малая функция при
х х0.

24.

Свойство 2. Произведение конечного
числа бесконечно малых функций при
х х0 тоже бесконечно малая функция
при х х0.
Свойство 3. Произведение бесконечно
малой
функции
на
функцию,
ограниченную в окрестности точки х=х0
является бесконечно малой функцией
при х х0.

25.

Свойство 4.
Частное от деления бесконечно малой
функции на функцию, предел которой
не равен нулю, есть величина
бесконечно малая.

26.

Свойство 5.
Для того, чтобы
lim f ( x) A
x
необходимо и достаточно выполнение
условия f(x)–A= (x), где (x) –
бесконечно малая функция.

27.

Свойство 6.
Если (х)~ (х) и (х)~ (х), то (х)~ (х) .

28.

Свойство 7.
Если (х)~ 1(х) и (х)~ 1(х) и
то
( x)
1 ( x)
lim
k
lim
k,
x x0 ( x )
x x0 ( x)
1
или
( x)
1 ( x)
lim
lim
.
x x0 ( x )
x x0 ( x )
1

29.

Литература
1. М. Л. Краснов, А. И. Киселев, Г. И.
Макаренко, Е. В. Шикин, В. И. Заляпин
Вся высшая математика. Том 1. Учебник.
(линейная алгебра и аналитическая
геометрия, введение в математический
анализ). -М.: Едиториал УРСС, 2012 – с.194206.