Similar presentations:
Предел и непрерывность функции
1.
Федеральное государственное бюджетное образовательное учреждениевысшего образования
«Оренбургский государственный университет»
Кафедра прикладной математики
И.Г. Руцкова
Электронный курс лекций «Математический анализ»,
часть 3
Оренбург 2017
2.
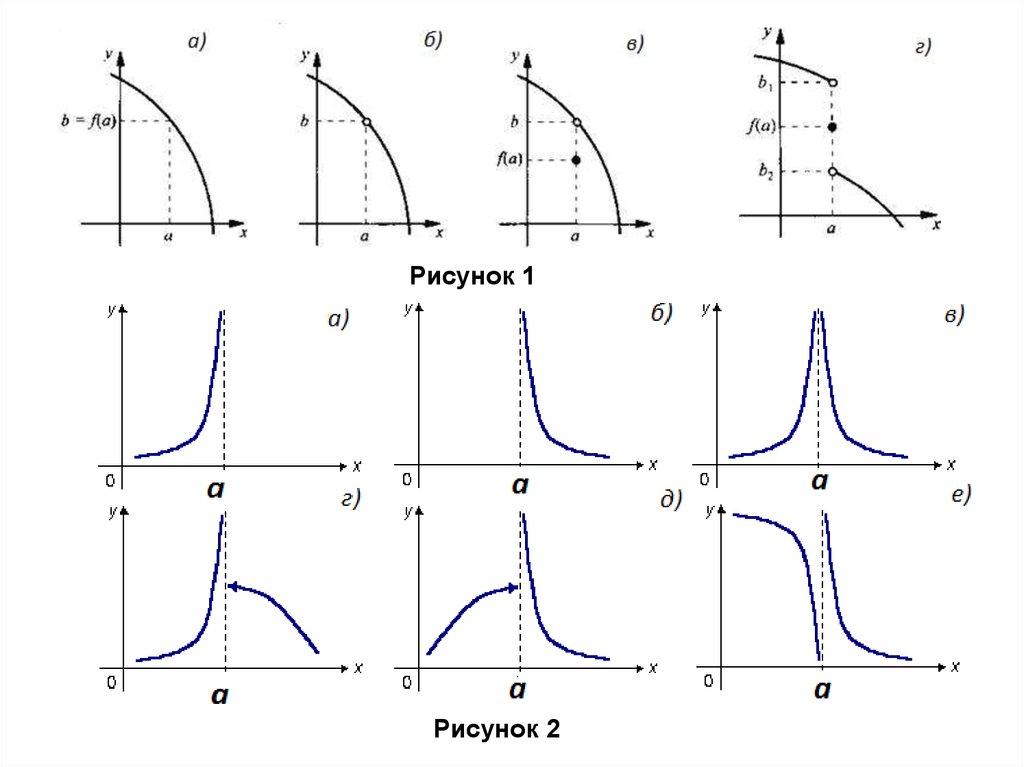
Рисунок 1Рисунок 2
3. Термины и обозначения
4. Предел функции при
x a5.
Предел функции в точке0 x a
x a ,
x a ,
a x a ,
x a,
x a.
x a,
f x A
0 x a x U a
f x A
A f x A
f x A f x U A
6. Свойства функций, имеющих предел в точке
Доказательство.lim f x A,
x a
0
B A
2
lim f x B ,
A B
x a
U A U B
lim f x A 1 : f x U A , x U 1 a
x a
lim f x B δ2 ε :f x U ε B , x U δ2 a
x a
min 1 ; 2
x U a
f x U A ,
f x U B ;
f x U A U B
Противоречие!
7. Свойства функций, имеющих предел в точке
Доказательство.A lim f x 0 0 : f x A , x U a
x a
1 : f x A 1, x U 1
,
a b a b,
a ,b R
f x A f x A 1,
f x A 1, x U 1 a ;
Доказательство.
x U δ 1 a ;
f x A 1, x U 1 a ;
С max A 1; f a
C A 1
8. Свойства функций, имеющих предел в точке
Доказательство. Изучите самостоятельноДоказательство. Изучите самостоятельно
9. Свойства функций, имеющих предел в точке
Доказательство. Изучите самостоятельноДоказательство. Изучите самостоятельно
10. Свойства функций, имеющих предел в точке
Доказательство. Изучите самостоятельноДоказательство. Докажите самостоятельно
Доказательство. Докажите самостоятельно
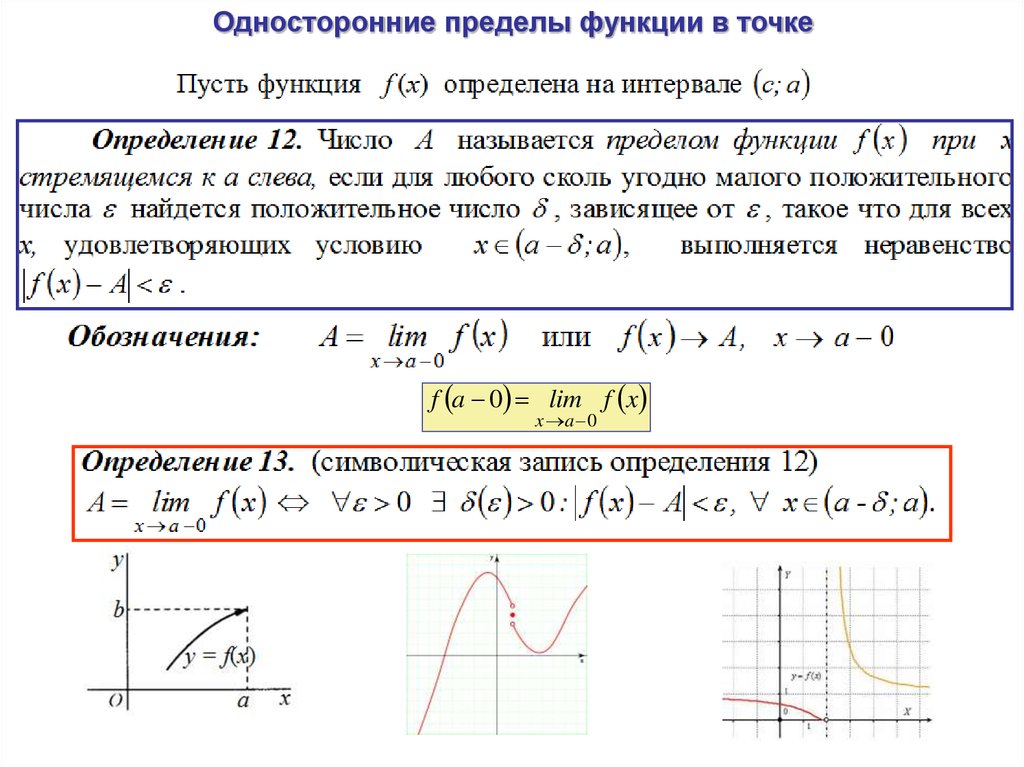
11. Односторонние пределы функции в точке
f a 0 lim f xx a 0
12. Односторонние пределы функции в точке
f a 0 lim f xx a 0
13. Односторонние пределы функции в точке
Доказательство.0 0 :
f x A ,
x U a
U a a ; a a; a
0 0 :
f x A ,
x a; a
0 0 :
f x A ,
x a ; a
lim f x A
x a 0
lim f x A
x a 0
lim f x A
1 0 :
f x A ,
x а; а 1 ;
lim f x A
2 0 :
f x A ,
x а 2 ; а ;
x a 0
x a 0
min 1 ; 2
x a ; a a; a U a
f x A
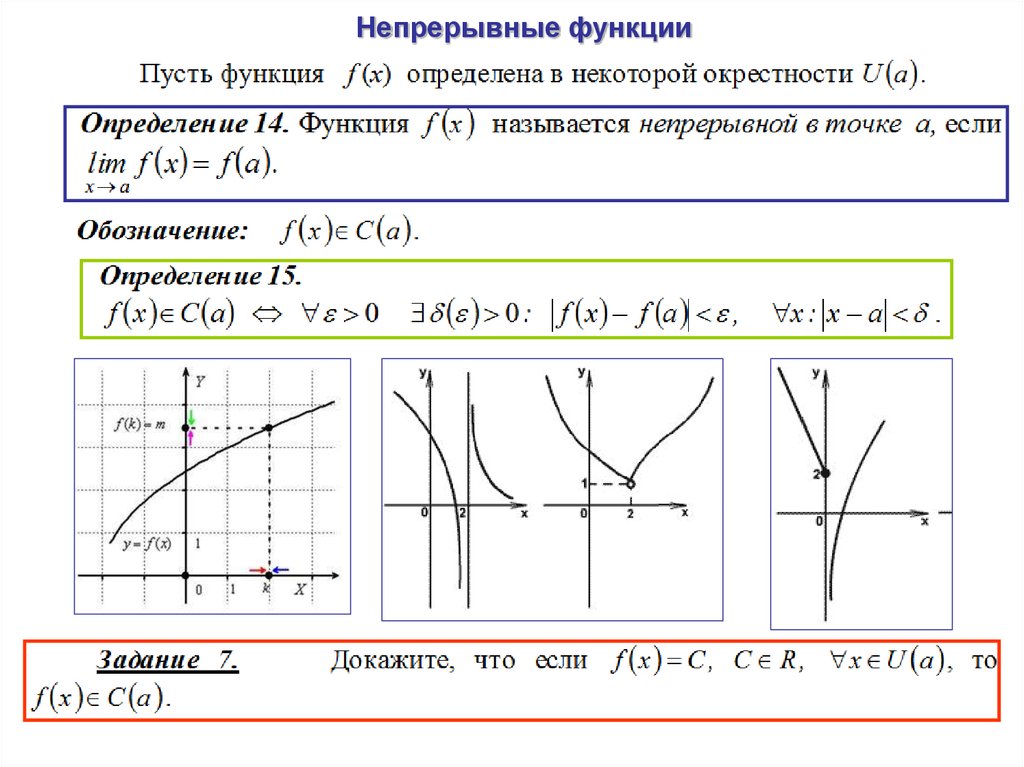
14.
15. Непрерывные функции
16. Непрерывные функции
Доказательство.lim f x f a , lim g x g a
x a
x a
1 ) lim x lim f x g x f a g a a
x C a
2 ) lim x lim f x g x f a g a a
x C a
x a
x a
x a
x a
3 ) lim x lim f x g x f a g a a
x a
x a
f x f a
a , g a 0
x a g x
g a
4 ) lim x lim
x a
x C a
x C a
17. Непрерывные функции
Доказательство. Изучите самостоятельно.18. Односторонняя непрерывность функции в точке
Доказательство. Проведите самостоятельно.19.
Непрерывность простейших (основных) элементарных функций20.
Непрерывность элементарных функцийПримеры:
y x x2 ,
Доказательство.
y tg ln x
21.
Некоторые практические правила вычисления предела функции в точке22.
Бесконечно малые и бесконечно большие функции, их свойстваДоказательство. Проведите самостоятельно.
Доказательство. Проведите самостоятельно.
23.
Бесконечно малые и бесконечно большие функции, их свойстваДоказательство. Проведите самостоятельно.
24.
Бесконечно малые и бесконечно большие функции, их свойстваДоказательство. Проведите самостоятельно.
25.
Бесконечно малые и бесконечно большие функции, их свойстваДоказательство. Проведите самостоятельно.
Доказательство. Проведите самостоятельно.
26.
Бесконечно малые и бесконечно большие функции, их свойства27.
Бесконечно малые и бесконечно большие функции, их свойства28.
Бесконечно малые и бесконечно большие функции, их свойстваДоказательство. Проведите самостоятельно.
29.
Бесконечно малые и бесконечно большие функции, их свойстваДоказательство. Проведите самостоятельно.
30. Список использованных источников
12
3
4
5
6
7
8
9
http://compendium.su/mathematics/algebra10/38.html
http://www.academiaxxi.ru/WWW_Books/HM/Ma/01/02/t.htm
https://it.rfei.ru/course/~Eyun/~I8wki7/~OvpMiq
http://ru.solverbook.com/spravochnik/predely/odnostoronnie-predely/
http://mathprofi.absolom.ru/nepreryvnost_funkcii_i_tochki_razryva.html
http://dic.academic.ru/dic.nsf/ruwiki/1059801
http://mathprofi.ru/nepreryvnost_funkcii_i_tochki_razryva.html
http://festival.1september.ru/articles/211285/
http://math-helper.ru/vyisshaya-matematika/nepreryivnost-i-tochkirazryiva-funktsii-primeryi-praktikum-po-matematicheskomu-analizu-urok-23
10 http://natalibrilenova.ru/blog/1261-elementarnye-funkcii.html



























 mathematics
mathematics








