Лекция 3_Проецирование плоскости_Строительство

1. Лекция 3 Тема: Проецирование плоскости

ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ И ГРАФИКИ
Лекция 3
Тема: Проецирование плоскости
РАЗРАБОТАЛИ: ст. преп. кафедры Н Г и Г – Крамаровская В.И.
ст. преп. кафедры Н Г и Г – Стаселько О.Л.
ст. преп. кафедры Н Г и Г – Шушарина И.В.

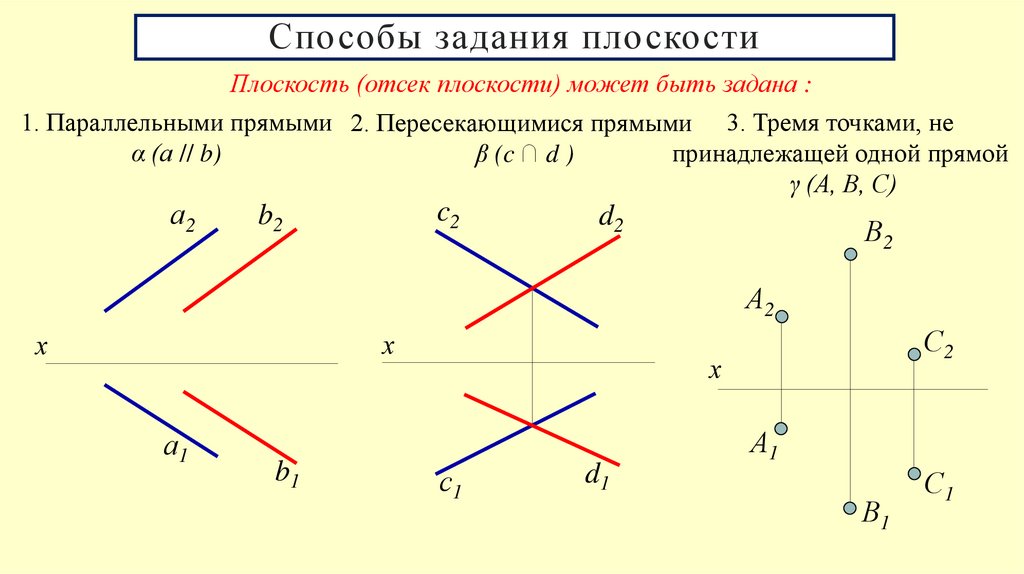
2. Способы задания плоскости

Плоскость (отсек плоскости) может быть задана :
1. Параллельными прямыми 2. Пересекающимися прямыми 3. Тремя точками, не
α (а // b)
принадлежащей одной прямой
β (c ∩ d )
γ (А, В, С)
а2
c2
b2
d2
В2
А2
х
х
а1
b1
С2
х
с1
d1
А1
В1
С1

3.

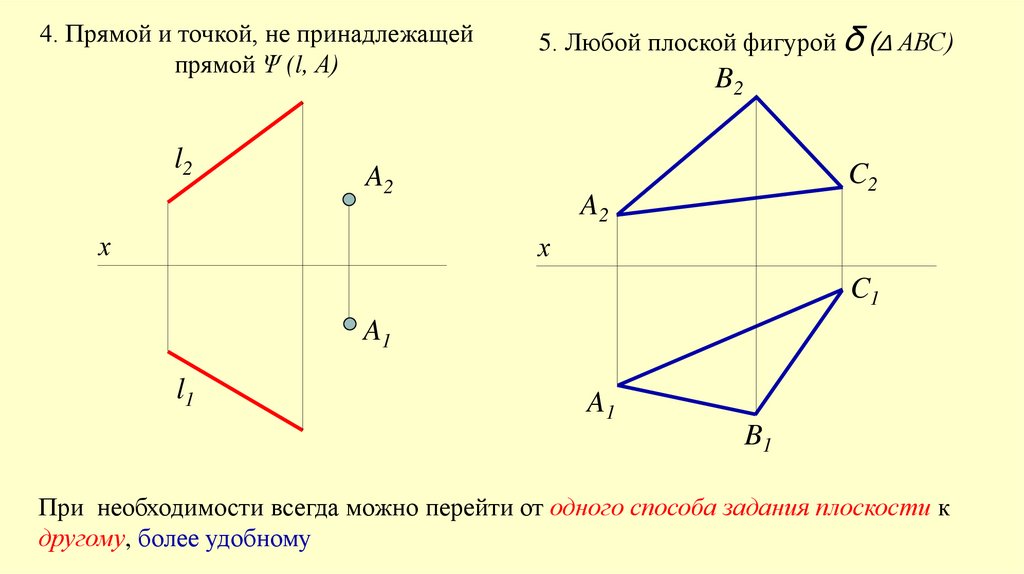
4. Прямой и точкой, не принадлежащей
прямой Ψ (l, А)
l2
5. Любой плоской фигурой δ (Δ АВС)
B2
A2
х
C2
A2
х
C1
A1
l1
A1
B1
При необходимости всегда можно перейти от одного способа задания плоскости к
другому, более удобному

4.

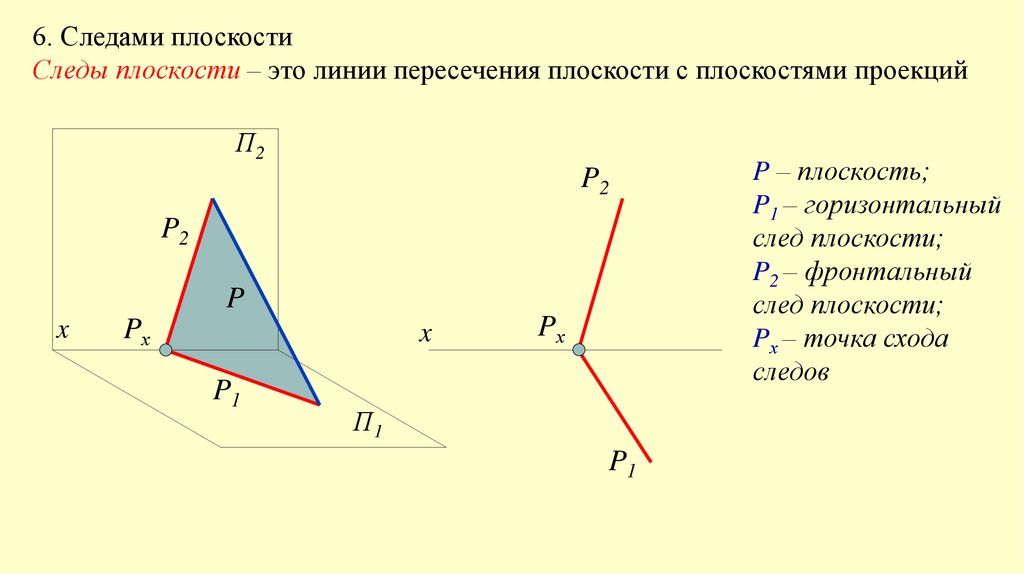
6. Следами плоскости
Следы плоскости – это линии пересечения плоскости с плоскостями проекций
П2
P2
P2
P
x
Pх
x
P1
Pх
П1
P1
P – плоскость;
P1 – горизонтальный
след плоскости;
P2 – фронтальный
след плоскости;
Pх – точка схода
следов

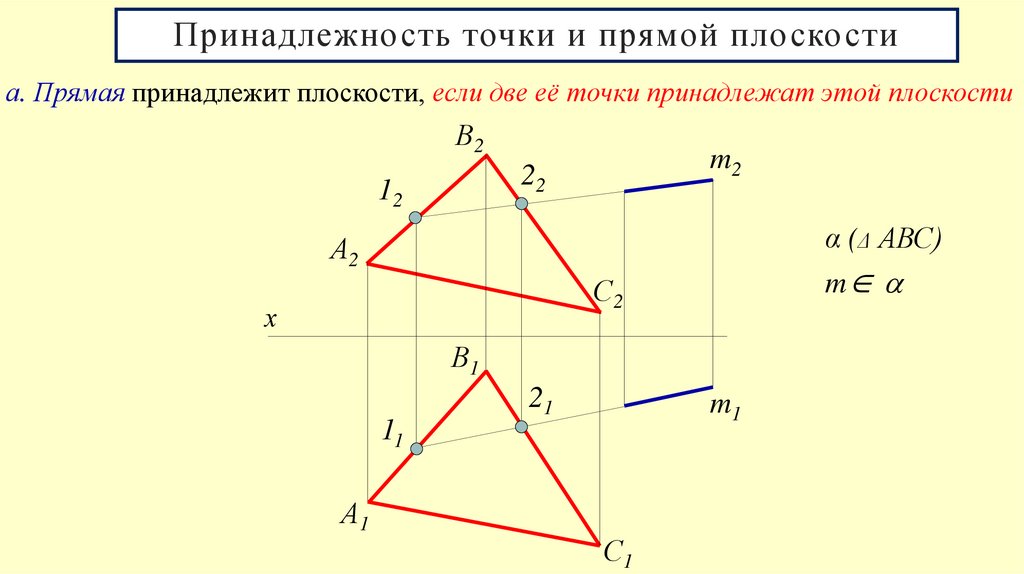
5. Принадлежность точки и прямой плоскости

а. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости
В2
m2
22
12
α (Δ АВС)
m
А2
С2
х
В1
21
m1
11
А1
С1

6.

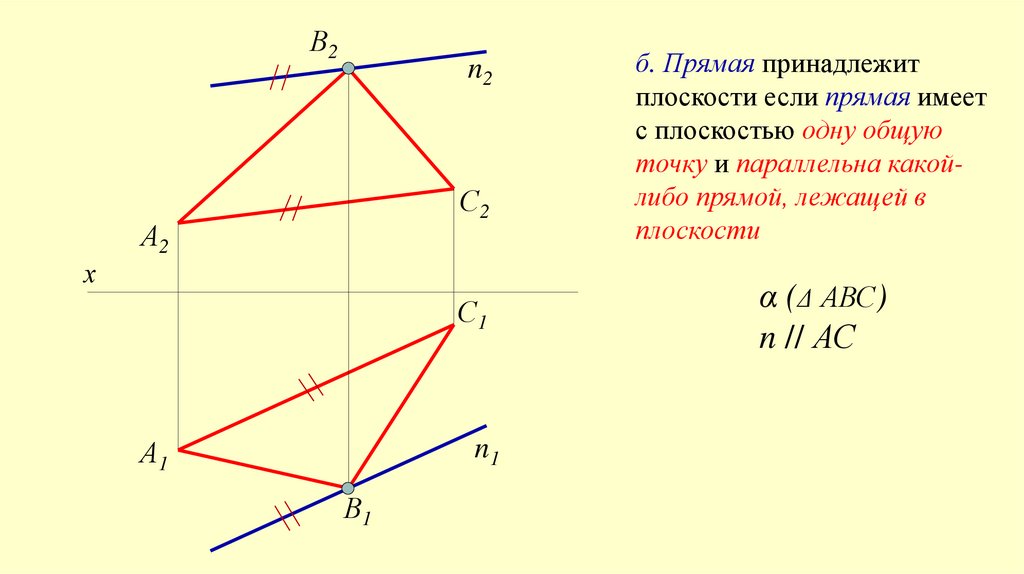
В2
n2
С2
А2
х
С1
А1
n1
В1
б. Прямая принадлежит
плоскости если прямая имеет
с плоскостью одну общую
точку и параллельна какойлибо прямой, лежащей в
плоскости
α (Δ АВС)
n // АС

7.

В2
12
К2
С2
А2
х
С1
11
А1
К1
В1
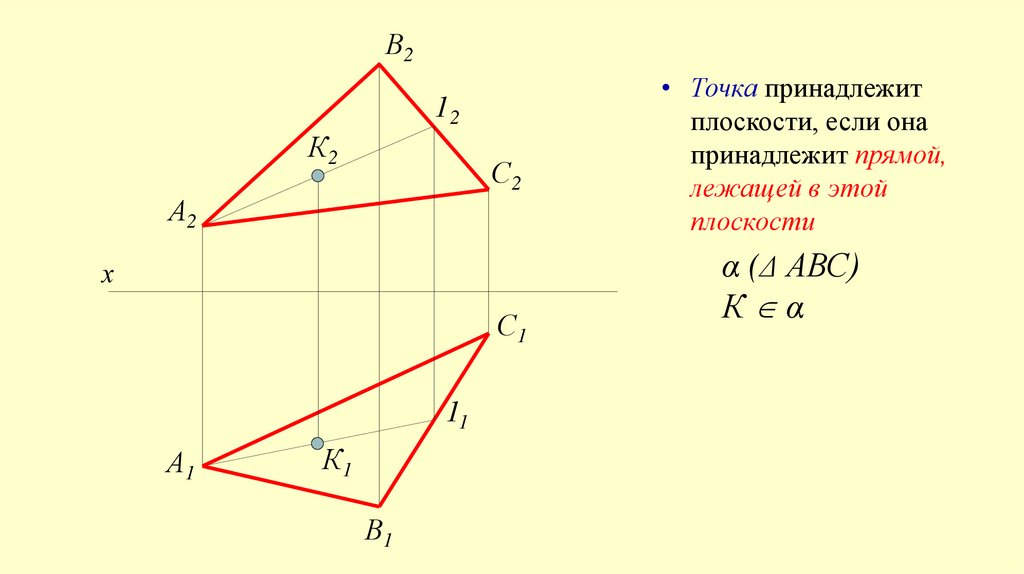
• Точка принадлежит
плоскости, если она
принадлежит прямой,
лежащей в этой
плоскости
α (Δ АВС)
К α

8.

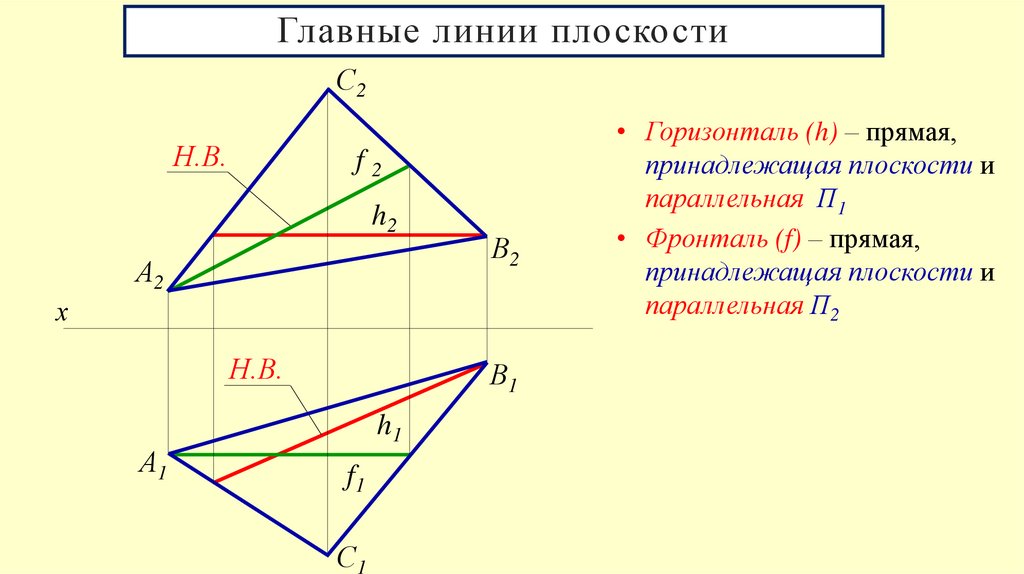
Главные линии плоскости
С2
Н.В.
f2
h2
А2
В2
х
Н.В.
А1
В1
h1
f1
С1
• Горизонталь (h) – прямая,
принадлежащая плоскости и
параллельная П1
• Фронталь (f) – прямая,
принадлежащая плоскости и
параллельная П2

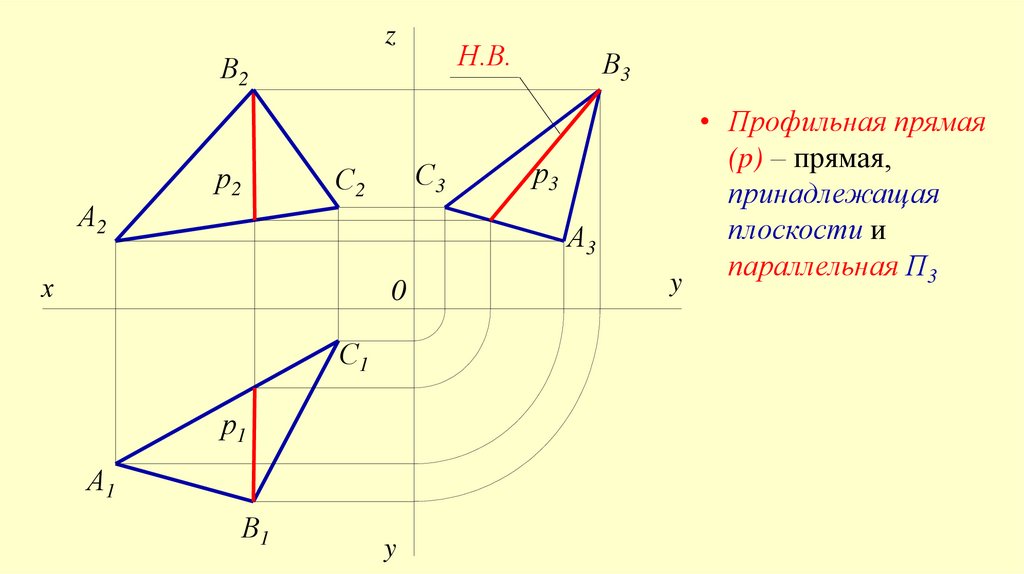
9. Главные линии плоскости

z
Н.В.
В2
А2
р2
С3
С2
В3
р3
А3
х
0
С1
р1
А1
В1
y
y
• Профильная прямая
(p) – прямая,
принадлежащая
плоскости и
параллельная П3

10.

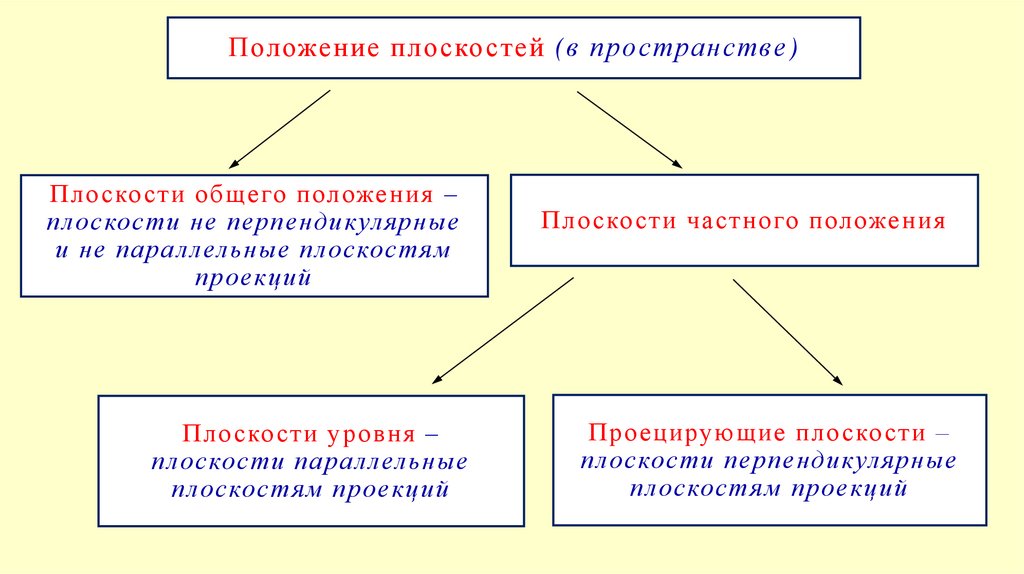
Положение пло ско стей (в пространстве)
Пло ско сти общего положения –
плоскости не перпендикулярные
и не паралл ельные плоскостям
проекций
Пло ско сти уровня –
плоскости паралл ельные
плоскостям проекций
Пло ско сти частного положения
Проецирующие пло ско сти –
плоскости перпендикулярные
плоскостям проекций

11.

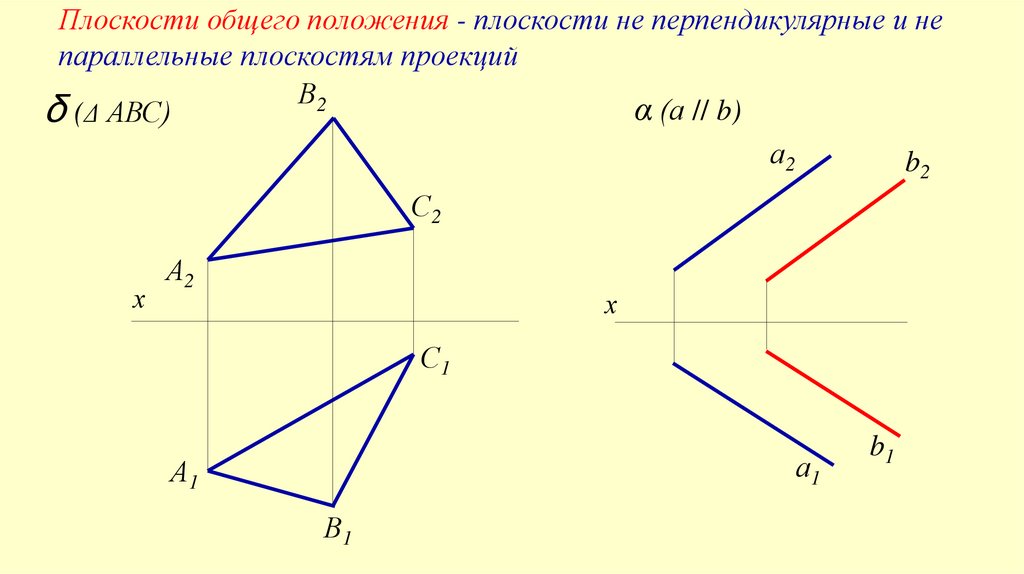
Плоскости общего положения - плоскости не перпендикулярные и не
параллельные плоскостям проекций
В2
α (а // b)
δ (Δ АВС)
а2
b2
С2
х
А2
х
С1
а1
А1
В1
b1

12.

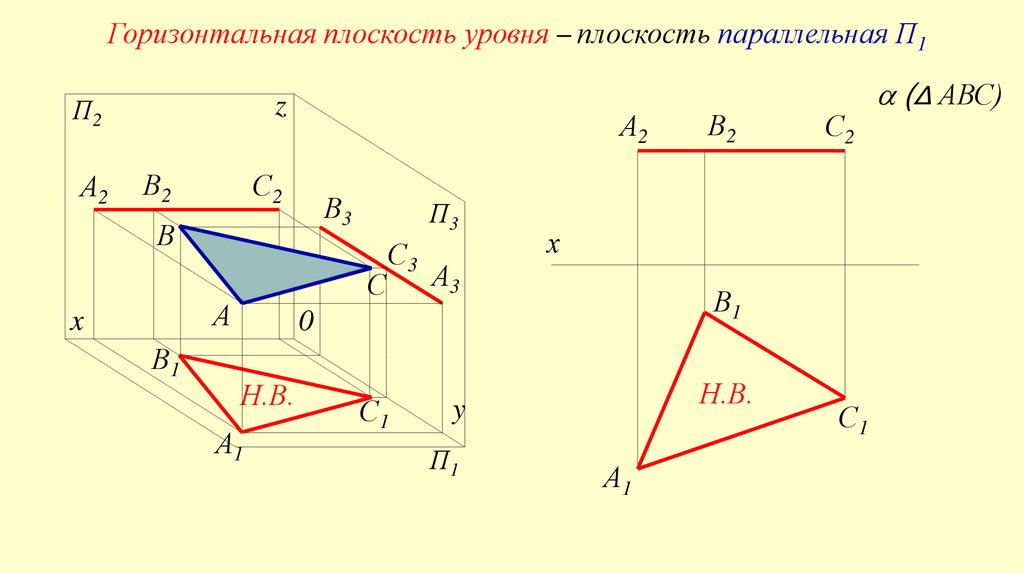
Горизонтальная плоскость уровня – плоскость параллельная П1
z
П2
А2
В2
А2
С2
В3
В
С
А
x
В1
П3
С3
А3
А1
С1
В1
Н.В.
y
П1
С2
х
0
Н.В.
В2
А1
С1
(Δ АВС)

13.

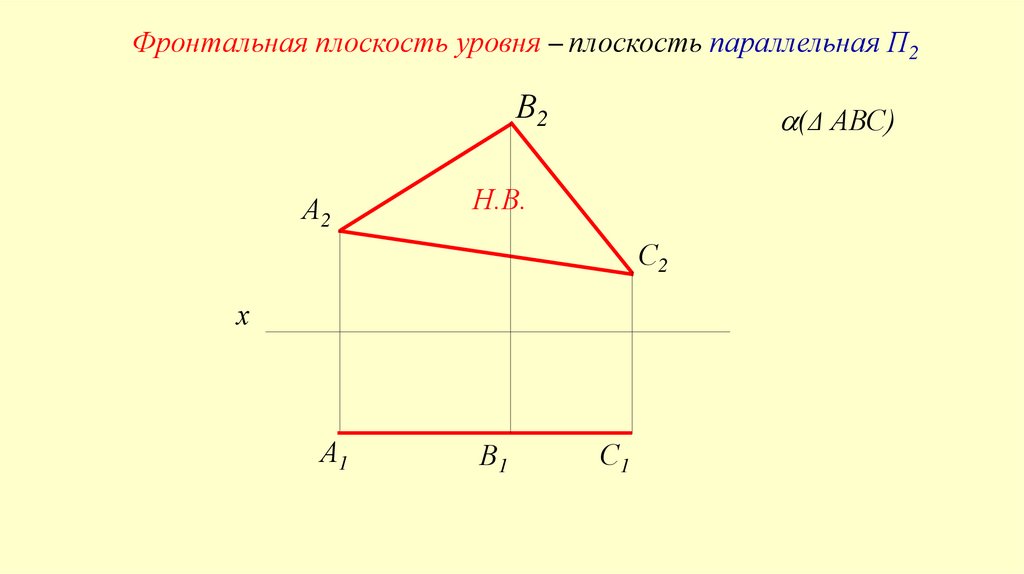
Фронтальная плоскость уровня – плоскость параллельная П2
В2
А2
(Δ АВС)
Н.В.
С2
х
А1
В1
С1

14.

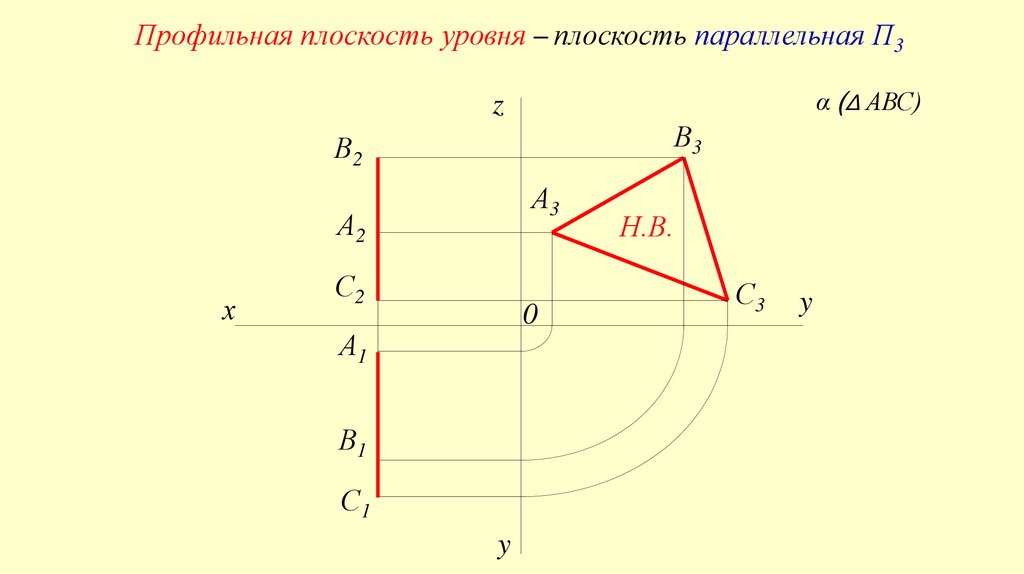
Профильная плоскость уровня – плоскость параллельная П3
α (Δ АВС)
z
В3
В2
А3
А2
х
С2
0
А1
В1
С1
y
Н.В.
С3
y

15.

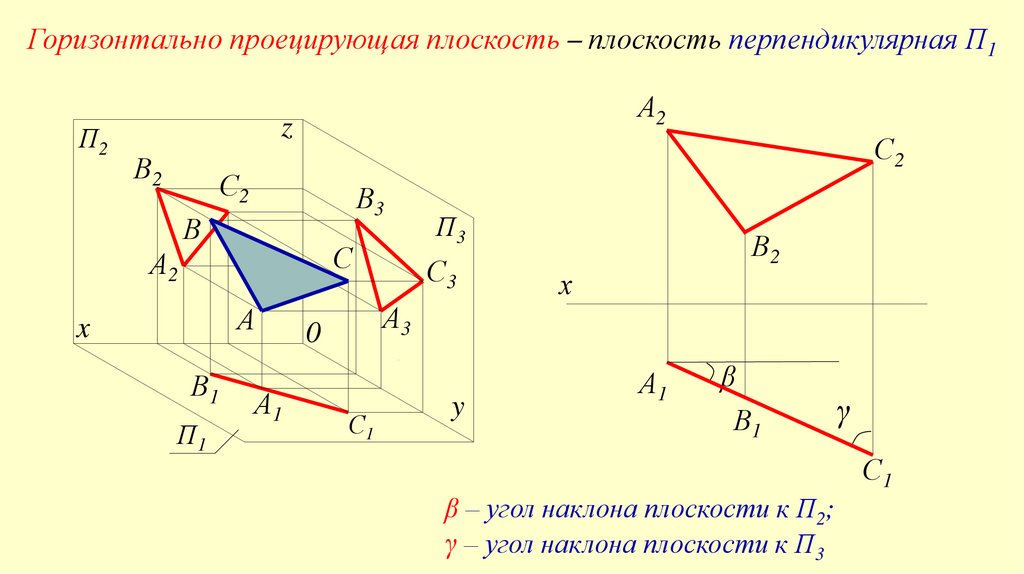
Горизонтально проецирующая плоскость – плоскость перпендикулярная П1
П2
А2
z
В2
С2
С2
В3
В
С
А2
А
x
В1
П1
А1
П3
С3
В2
х
А3
0
С1
y
А1
β
В1
γ
С1
β – угол наклона плоскости к П2;
γ – угол наклона плоскости к П3

16.

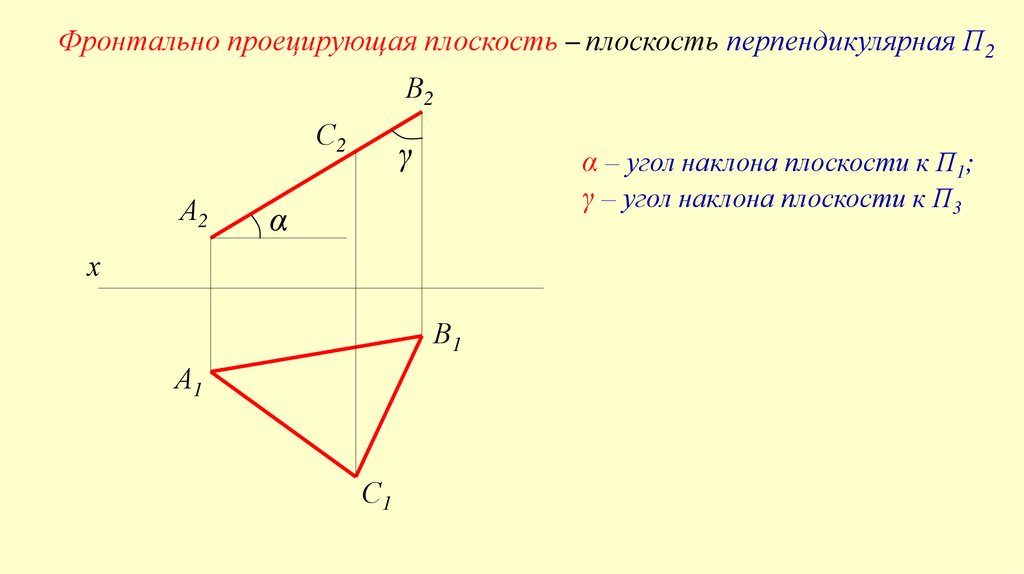
Фронтально проецирующая плоскость – плоскость перпендикулярная П2
В2
С2
А2
γ
α – угол наклона плоскости к П1;
γ – угол наклона плоскости к П3
α
х
В1
А1
С1

17.

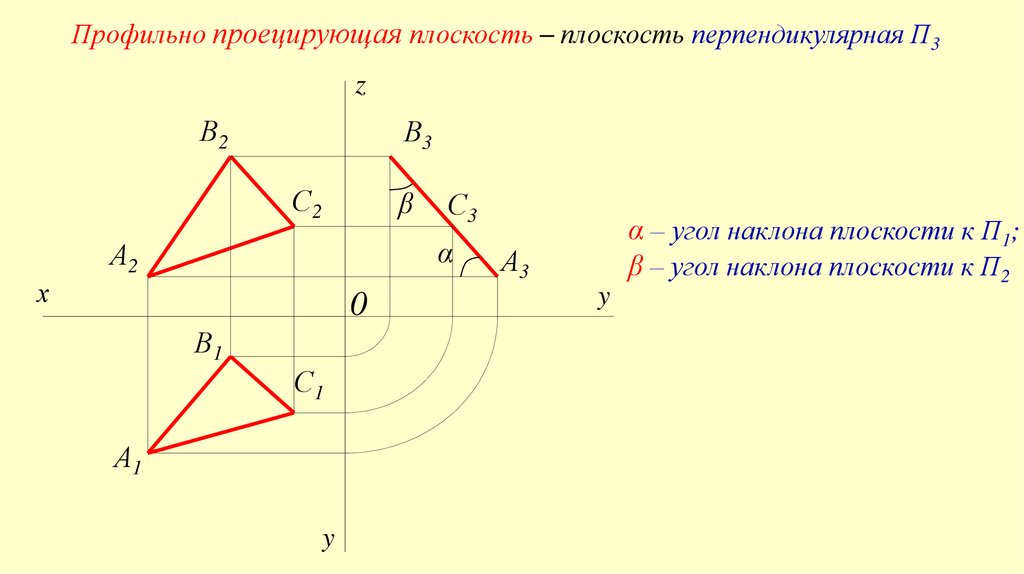
Профильно проецирующая плоскость – плоскость перпендикулярная П3
z
В2
В3
С2
β
С3
α
А2
х
0
В1
С1
А1
y
А3
y
α – угол наклона плоскости к П1;
β – угол наклона плоскости к П2

18.

• Каждая из плоскостей уровня на плоскость проекций, которой она
параллельна, проецируются без искажения, то есть в натуральную
величину
• Каждая из проецирующих плоскостей, то есть перпендикулярных
плоскостям проекций, обладает собирательным свойством – все,
что лежит в плоскости (точки, линии) проецируется в следпроекцию

19.

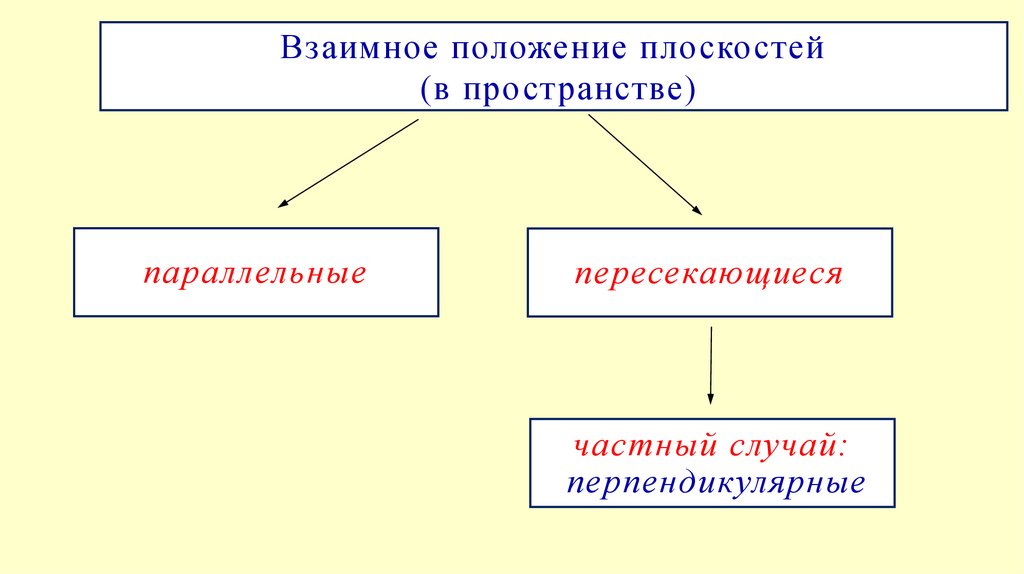
Взаимное положение плоскостей
(в пространстве)
параллельные
пересекающиеся
частный случай:
перпендикулярные

20.

В2
С2
А2
n2
m2
х
С1
m1
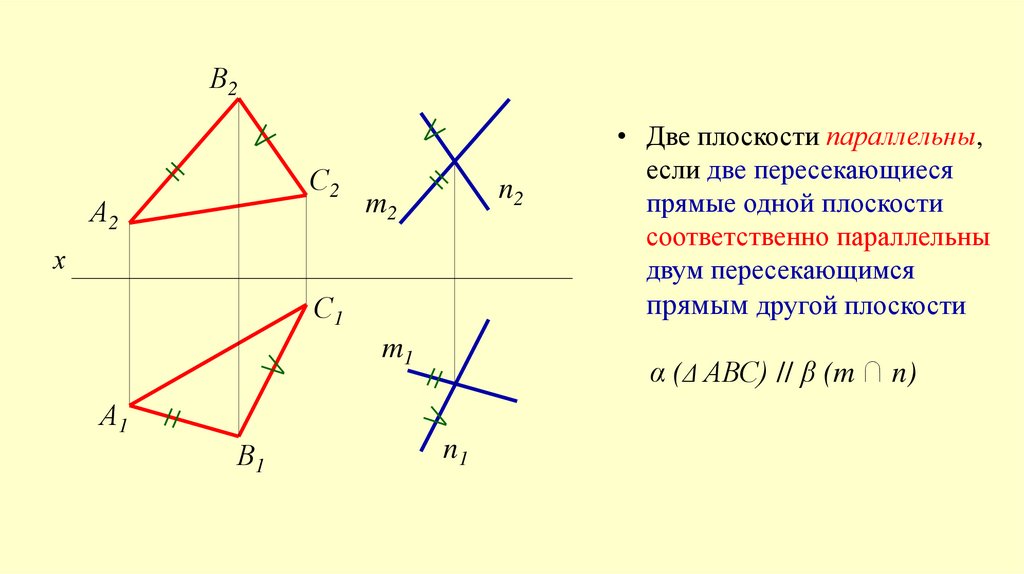
α (Δ АВС) // β (m ∩ n)
А1
В1
• Две плоскости параллельны,
если две пересекающиеся
прямые одной плоскости
соответственно параллельны
двум пересекающимся
прямым другой плоскости
n1

21.

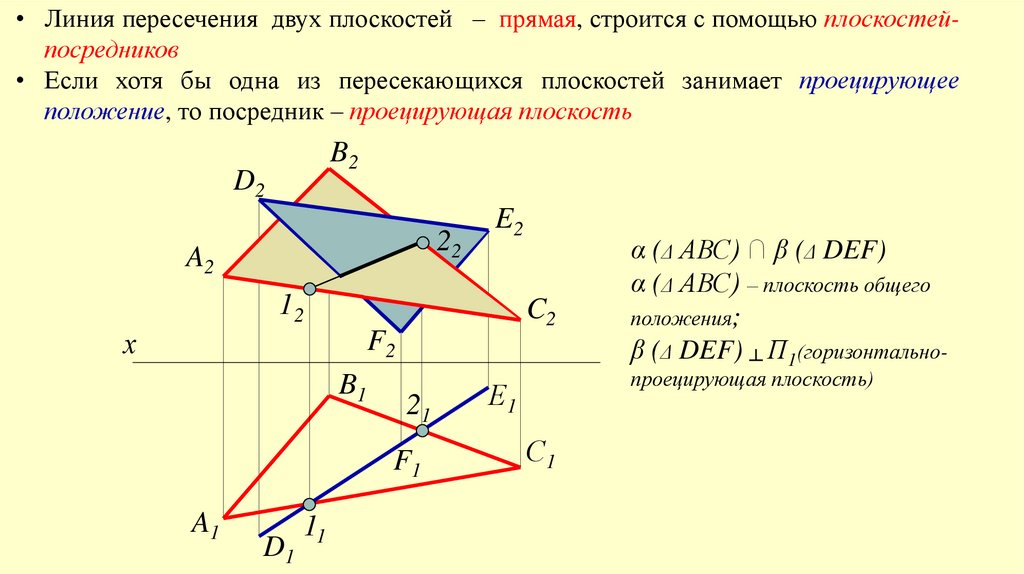
• Линия пересечения двух плоскостей – прямая, строится с помощью плоскостейпосредников
• Если хотя бы одна из пересекающихся плоскостей занимает проецирующее
положение, то посредник – проецирующая плоскость
B2
D2
22
A2
E2
12
х
C2
F2
B1
21
F1
A1
D1
11
α (Δ АВС) ∩ β (Δ DEF)
α (Δ АВС) – плоскость общего
положения;
β (Δ DEF) ┴ П1(горизонтальнопроецирующая плоскость)
Е1
С1

22.

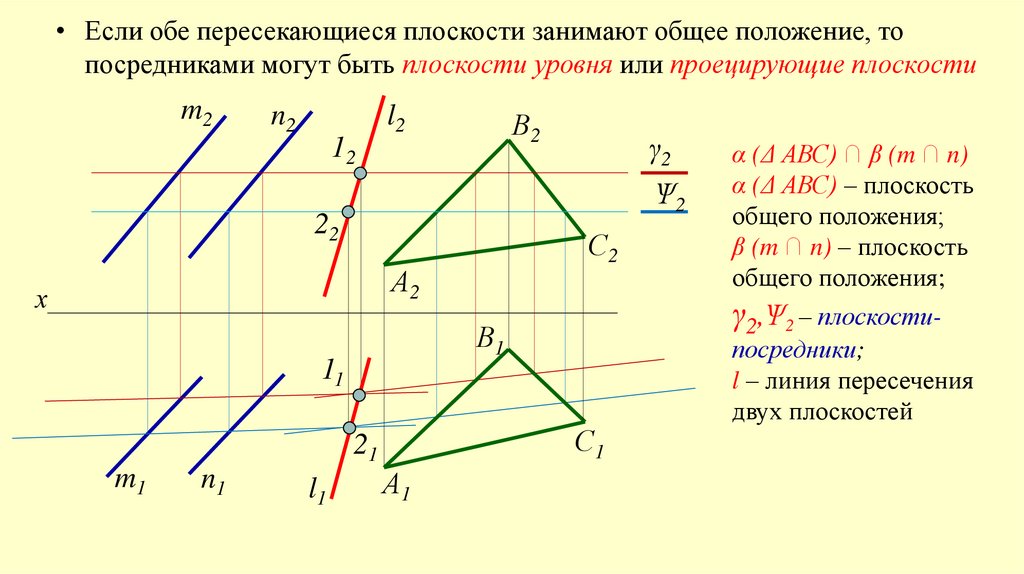
• Если обе пересекающиеся плоскости занимают общее положение, то
посредниками могут быть плоскости уровня или проецирующие плоскости
m2
n2
l2
В2
12
Ѱ2
22
С2
А2
х
С1
21
n1
l1
А1
α (Δ АВС) ∩ β (m ∩ n)
α (Δ АВС) – плоскость
общего положения;
β (m ∩ n) – плоскость
общего положения;
γ2,Ѱ2 – плоскости-
В1
11
m1
γ2
посредники;
l – линия пересечения
двух плоскостей

23.

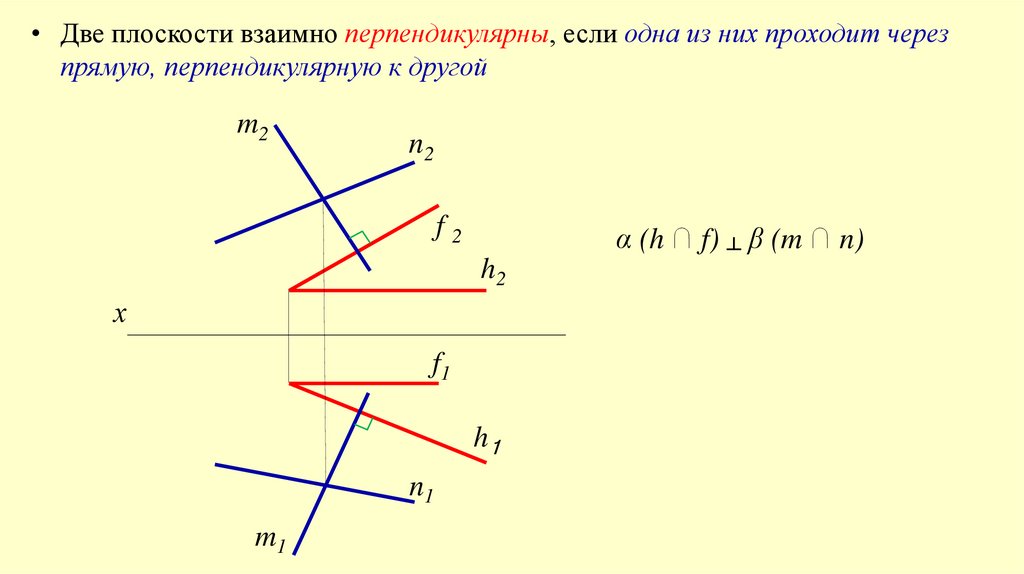
• Две плоскости взаимно перпендикулярны, если одна из них проходит через
прямую, перпендикулярную к другой
m2
n2
f2
h2
х
f1
h1
n1
m1
α (h ∩ f) ┴ β (m ∩ n)

24.

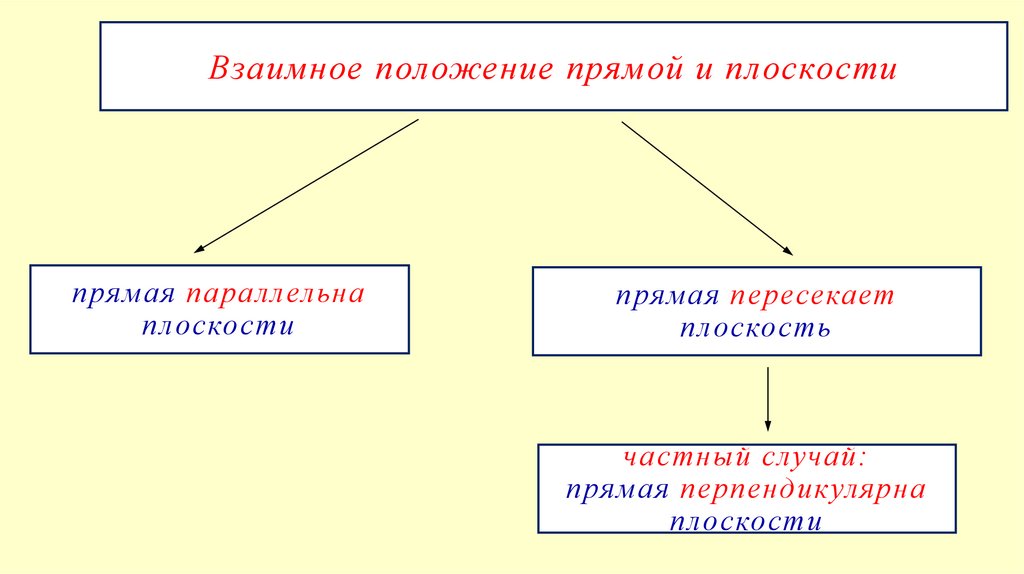
Взаимное положение прямой и плоскости
прямая параллельна
плоскости
прямая пересекает
плоскость
частный случай:
прямая перпендикулярна
плоскости

25.

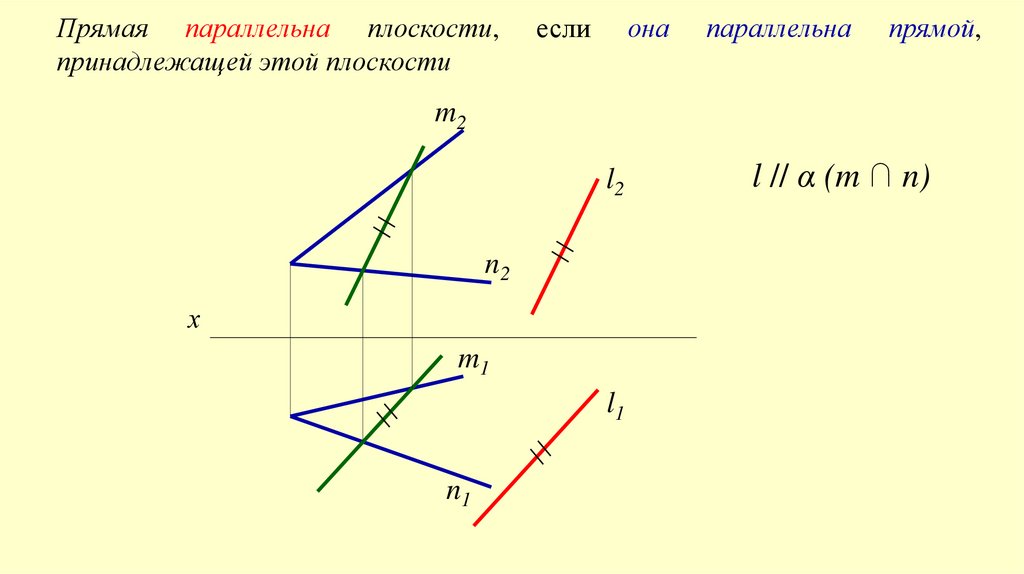
Прямая параллельна плоскости,
принадлежащей этой плоскости
если
она
параллельна
прямой,
m2
l2
n2
х
m1
l1
n1
l // α (m ∩ n)

26.

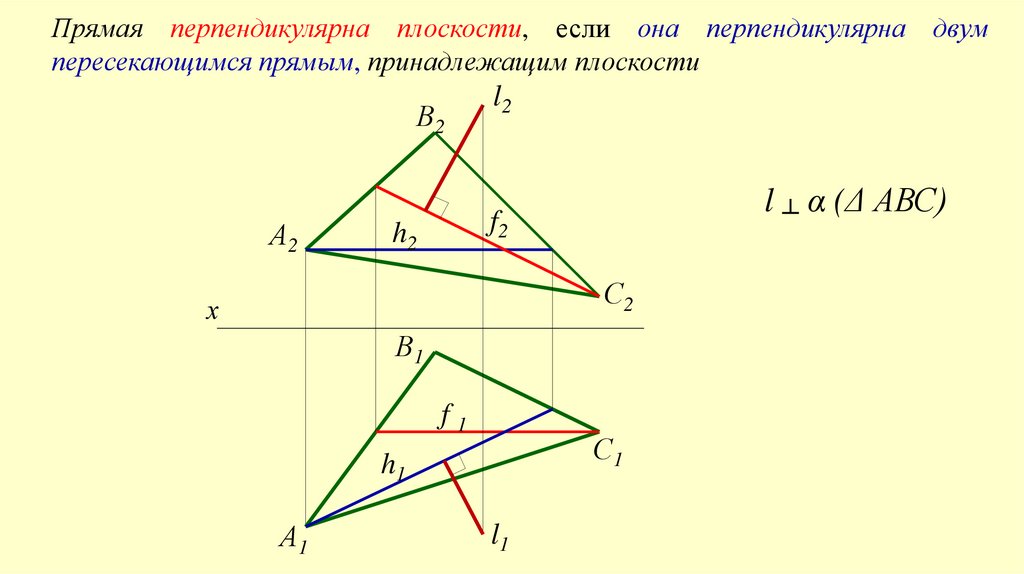
Прямая перпендикулярна плоскости, если она перпендикулярна двум
пересекающимся прямым, принадлежащим плоскости
В2
А2
l2
l ┴ α (Δ АВС)
f2
h2
С2
х
В1
f1
С1
h1
А1
l1

27.

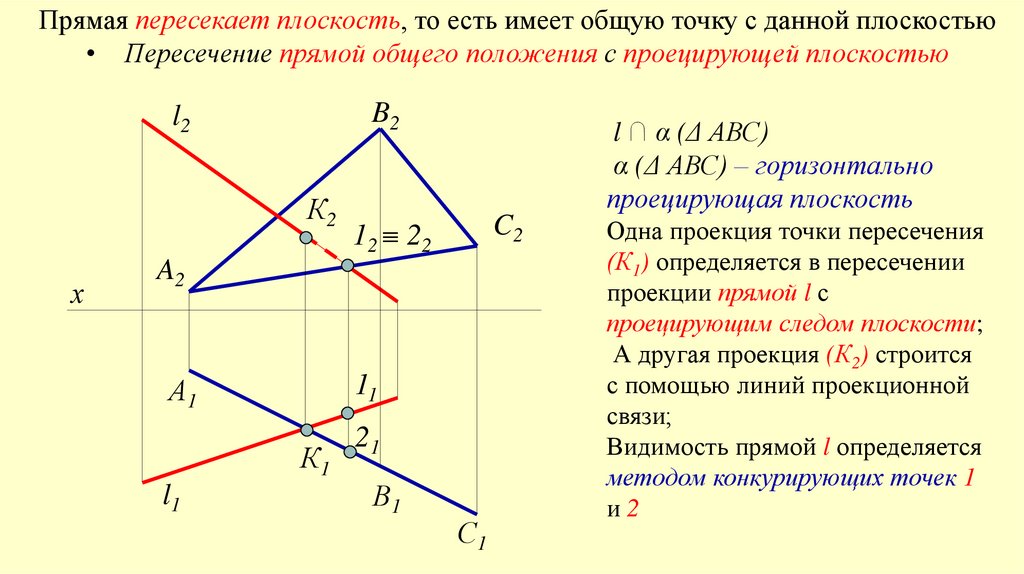
Прямая пересекает плоскость, то есть имеет общую точку с данной плоскостью
• Пересечение прямой общего положения с проецирующей плоскостью
B2
l2
К2
х
l ∩ α (Δ АВС)
α (Δ АВС) – горизонтально
проецирующая плоскость
C2
12 22
A2
А1
11
К1
l1
21
В1
С1
Одна проекция точки пересечения
(К1) определяется в пересечении
проекции прямой l с
проецирующим следом плоскости;
А другая проекция (К2) строится
с помощью линий проекционной
связи;
Видимость прямой l определяется
методом конкурирующих точек 1
и2

28.

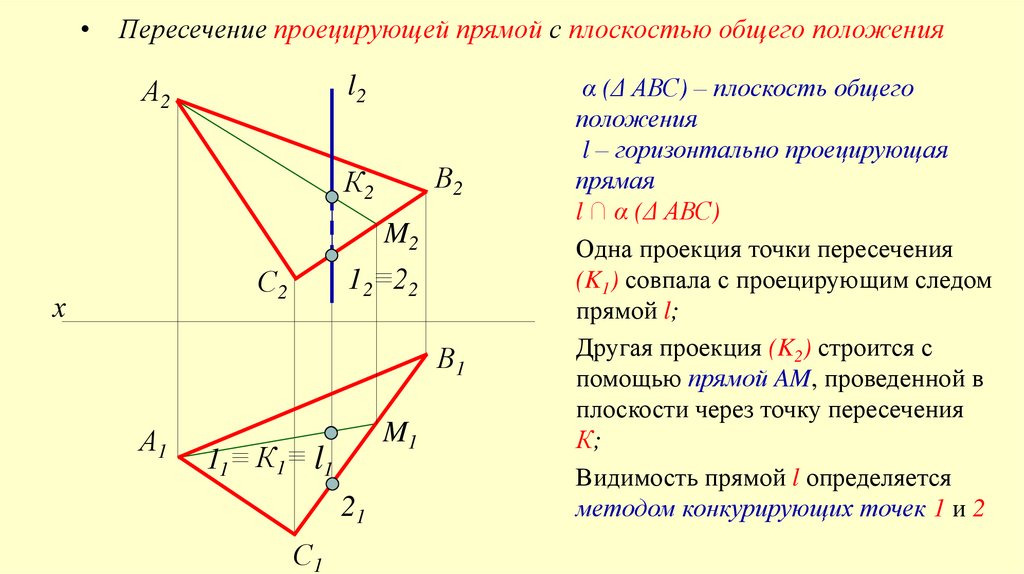
Пересечение проецирующей прямой с плоскостью общего положения
А2
l2
В2
К2
M2
12≡22
С2
х
В1
А1
M1
11≡ К1≡ l1
21
С1
α (Δ АВС) – плоскость общего
положения
l – горизонтально проецирующая
прямая
l ∩ α (Δ АВС)
Одна проекция точки пересечения
(K1) совпала с проецирующим следом
прямой l;
Другая проекция (K2) строится с
помощью прямой AM, проведенной в
плоскости через точку пересечения
К;
Видимость прямой l определяется
методом конкурирующих точек 1 и 2

29.

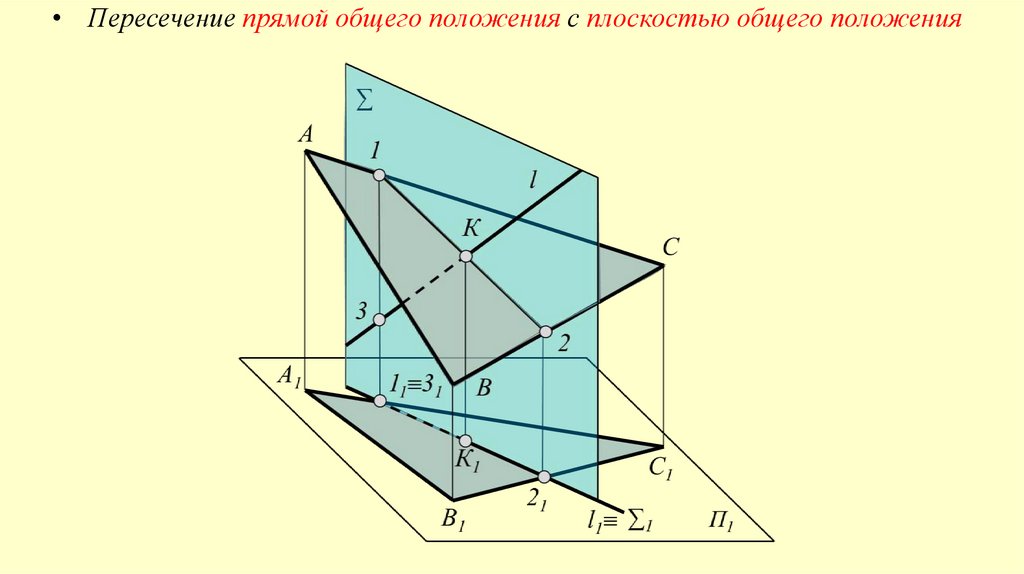
• Пересечение прямой общего положения с плоскостью общего положения

30.

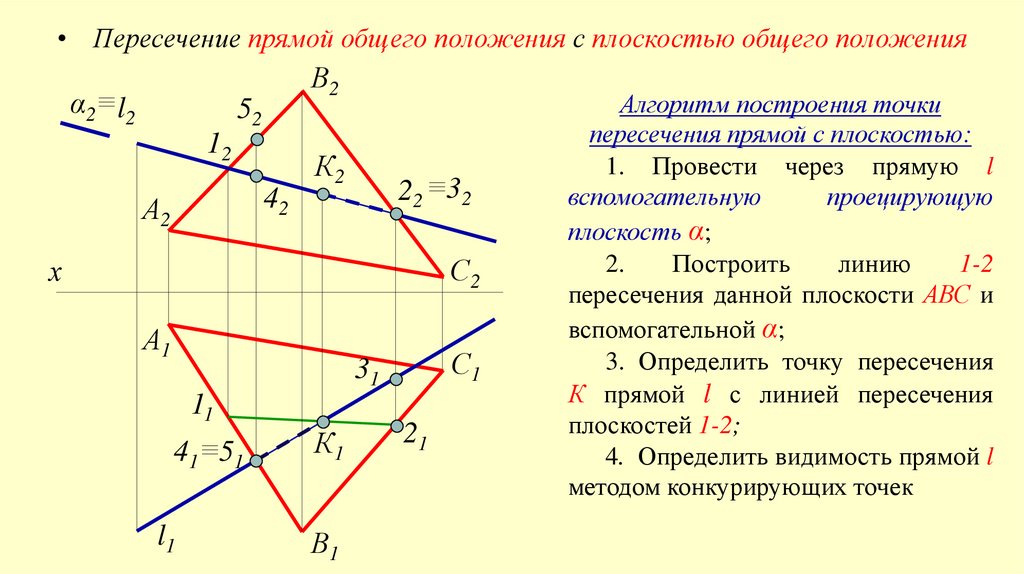
• Пересечение прямой общего положения с плоскостью общего положения
α2≡ l2
В2
52
12
42
А2
К2
22 ≡32
С2
х
А1
С1
31
11
41≡51
К1
l1
В1
21
Алгоритм построения точки
пересечения прямой с плоскостью:
1. Провести через прямую l
вспомогательную
проецирующую
плоскость α;
2.
Построить
линию
1-2
пересечения данной плоскости АВС и
вспомогательной α;
3. Определить точку пересечения
К прямой l с линией пересечения
плоскостей 1-2;
4. Определить видимость прямой l
методом конкурирующих точек

31.

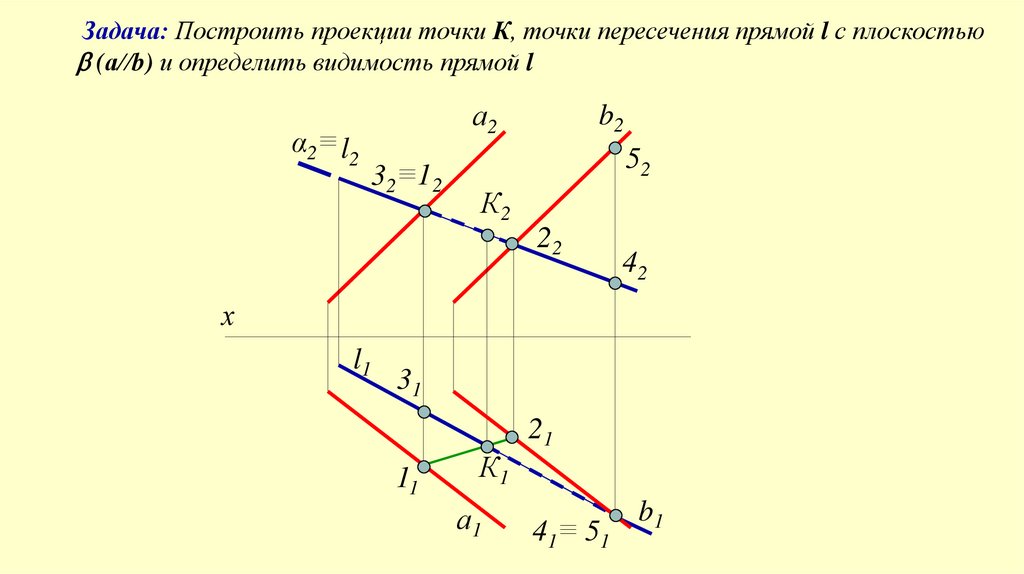
Задача: Построить проекции точки К, точки пересечения прямой l с плоскостью
(а//b) и определить видимость прямой l
α2≡ l2
а2
32≡12
b2
52
К2
22
42
х
l1
31
21
11
К1
а1
41≡ 51
b1