m3_lecter3_17

1.

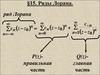
§ 7. Ряды Лорана
ОПР 23. Рядом Лорана называется ряд вида
cn z a n c n z a n c n 1 z a n 1 c 1 z a 1 c0 c1 z a c2 z a 2 cn z a n
n
или
1
c n
n
c
z
a
c
z
a
c
z
a
c
z
a
n
n
n
n
n
z
a
n
n
n 0
n 1
n 0
n
n
n
7.1
Ряд
cn z a n
называется правильной частью ряда Лорана. Область
сходимости круг | z − a | < R (включая R=0, R=∞).
n 0
1
Ряд
cn z a c n z a n
n
n
n 1
(*)
называется главной частью ряда Лорана.
Дальше не писать! Только ознакомиться
пропустить 30 клеточек

2.

Это не писать! Только ознакомиться
Теорема 7.1. (о представлении аналитической функции рядом Лорана ).
Всякая функция, аналитическая в кольце r <|z − a| <R может быть представлена
в этом кольце рядом Лорана
f ( z ) c n z a n
n
1
где c 2 i
n
f (t ) dt
C' t a
c
n 1
1
n
2 i f (t ) t a
n 1dt
пропустить 1 страницу
Теорема 7.2. (единственности разложения функции в ряд Лорана ).
Если c n z a n сходится к функции f( z ) в кольце r <|z − a| <R, то
n
1
f (t ) dt
коэффициенты c
определяются однозначно
2
i
n
n 1
C' t a
пропустить 1 страницу
7.2

3.

Это не писать! Только ознакомиться
Разложение функций в ряд Лорана в окрестности ∞.
ОПР 24.
1
Если для ряда Лорана по степеням z используем замену переменных ,
z
то получим ряд вида
f ( z ) c n z cn z n
n
n 1
n 0
сходящийся к f ( z ) в кольце R < | z | < ∞.
Говорят: функция разложена в ряд Лорана в окрестности z = ∞.