Similar presentations:
Ряды Лорана
1. §15. Ряды Лорана.
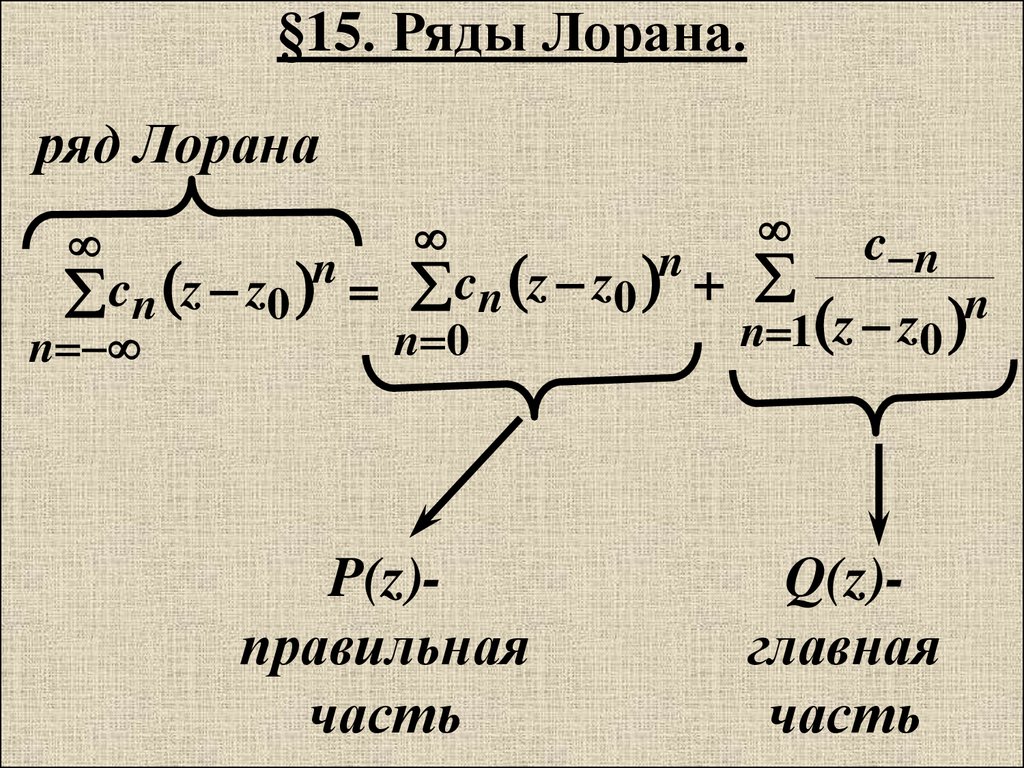
ряд Лоранаc n z z0 c n z z0
n
n
n 0
P(z)правильная
часть
n
c n
n 1 z z0
Q(z)главная
часть
n
2.
P z Сz z0 R1
1
Q z :
z z0
~
1
n
Q z Q c n С
R2
n 1
1
R2
обозначение радиуса сходимости
~
ряда Q
3.
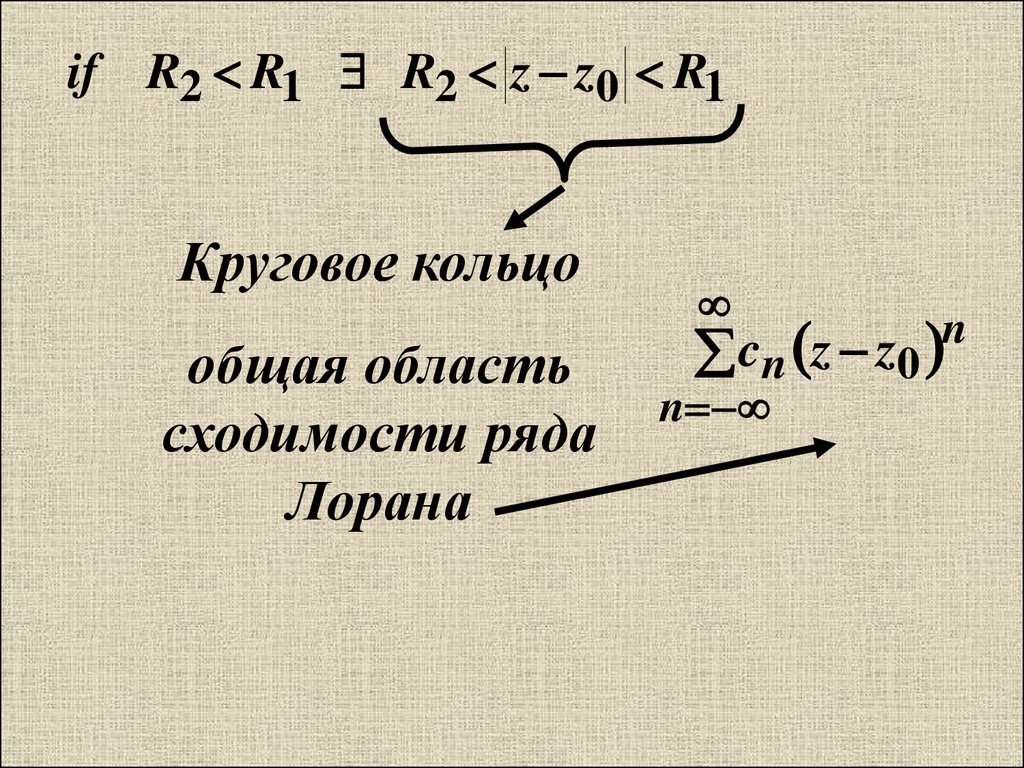
if R2 R1 R2 z z0 R1Круговое кольцо
общая область
сходимости ряда
Лорана
c n z z0
n
n
4. Следствия теоремы Абеля.
c n z z0 Сn
n
R2 z z0 R1
5.
2) Ряд Лорана внутри кольцасходимости
можно дифференцировать и
интегрировать почленно любое
число раз.
При этом полученные ряды также
С
R2 z z0 R1
6. 3)
1R1
L1 lim n cn
L1
n
R2 lim n c n
n
cn 1
L1 lim
n cn
c n 1
R2 lim
n c n
4) Коэффициенты ряда Лорана cn
через значения суммы ряда в точке z0
не определяются!
В точке z0 сумма ряда Лорана не
определена!
7. Теорема 15.1
Еслиf z С
R2 z z0 R1
! cn z z0 f z z : R2 z z0 R1 .
n
n
8.
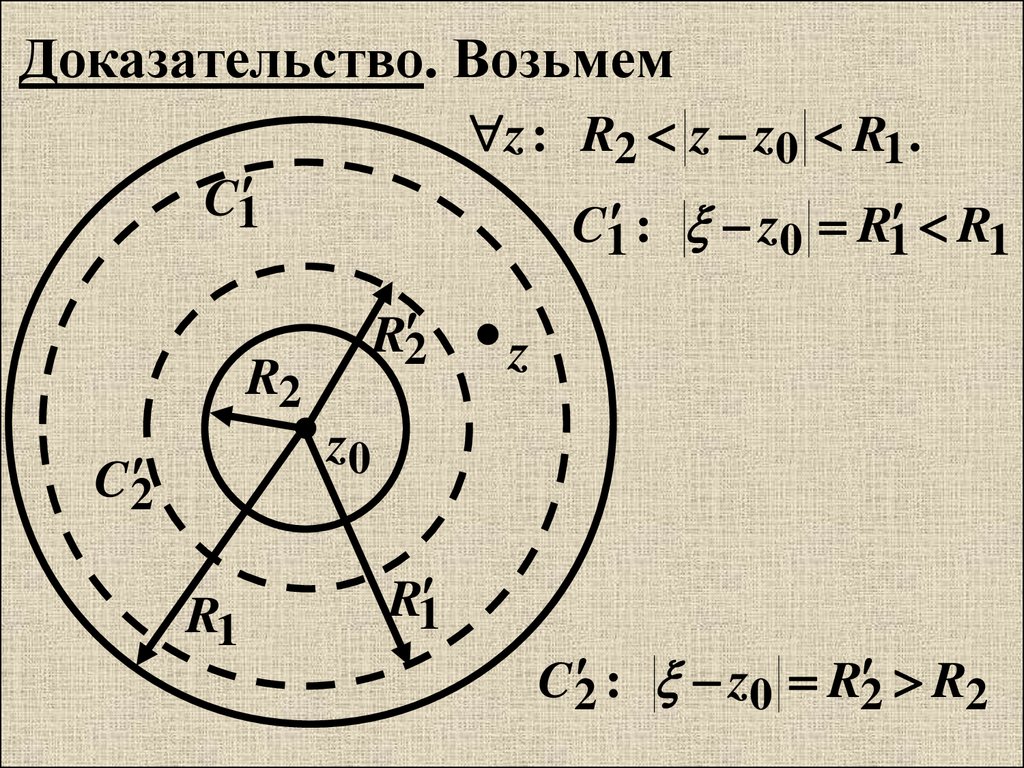
Доказательство. Возьмемz : R2 z z0 R1 .
C1 : z0 R1 R1
C1
R2
R2
z
z0
C 2
R1
R1
C 2 : z0 R2 R2
9.
f z Сz z0 R1
R2
f ( )
1
f ( )
f z
d
d
2 i ' z
2 i ' z
1
C1
P z Q z .
z z0
C1 :
q 1
z0
C2
10.
11
z z0 z z0
1
1
z0 1 z z0
z0
z z
1
0
z0 n 0 z0
n
Сходится равномерно по на C1
11.
1P z
n 0 2 i
f ( )
n
d z z0
n 1
z
'
0
C1
cn z z0 , где
n
n 0
cn
1
f ( )
2 i ' z0 n 1
C
1
d , n 0.
12.
C 2 :z0
z z0
1
1
1
z z0 z z0
1
1
z z0 1 z0
z z0
k
z0
1
k n 1
z z0 k 0 z z 0
n k 1
13.
Сходитсяn 1
z0
n
n 1 z z0
равномерно
по на C 2
c n
Q z
n 1 z z0
c n
1
n
n 1
f ( ) z0
2 i '
C
2
, n 0,
1
f ( )
2 i ' z0 n 1
C
2
d
d , n 0.
14.
cn1
f ( )
2 i C z0 n 1
d , n 0, 1, 2 .
где C- произвольный замкнутый
контур, лежащий в кольце
R2<|z-z0|<R1 и содержащий точку z0
внутри.
15.
f z c n z z0n
c n
n 1 z z0
n 0
n
c n z z0
n
n
cn
1
f ( )
2 i C z0 n 1
d , n .
16.
Т.к. z- внутри R2<|z-z0|<R1 =>c n z z0 f z
n
n
z : R2 z z0 R1 .
c n z z0 f z
n
n
R2 R2 z z0 R1 R1 .
17.
Докажем единственность.f z cn z z0 , n : cn cn
n
n
n
n
n
n
c n z z0 c n z z0
z : R2 z z0 R1 .
C R : z0 R, R2 R R1 .
18.
cn z0 fcn z0 f
n
n
n
n
m 1
d
m 1
d
d z0 R e
i
cn z0 z0
n
n
CR
n
CR
cn z0 z0
n
n m 1
z0
CR
19.
Rn m
2
i e
0
0, n m
d
2 i , n m
i n m
cn cn n
Точная область сходимости ряда
Лорана есть R2<|z-z0|<R1, на границах
которого имеется хотя бы по одной
особой точке аналитической функции
f(z) - суммы ряда (т. 13.1)





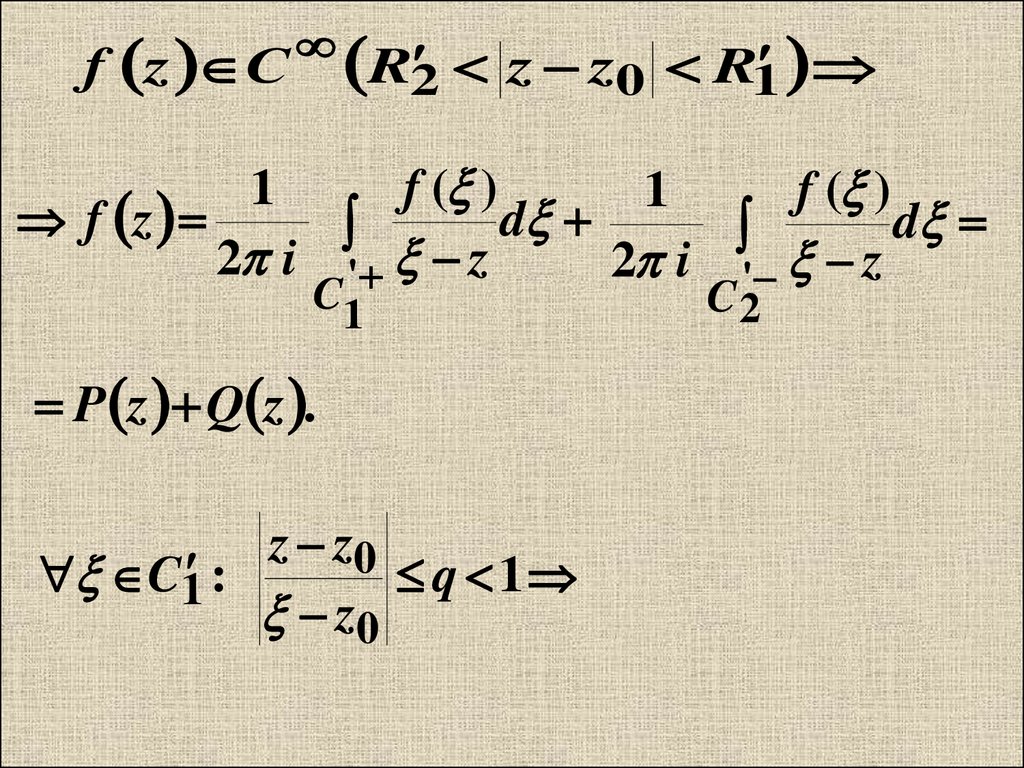

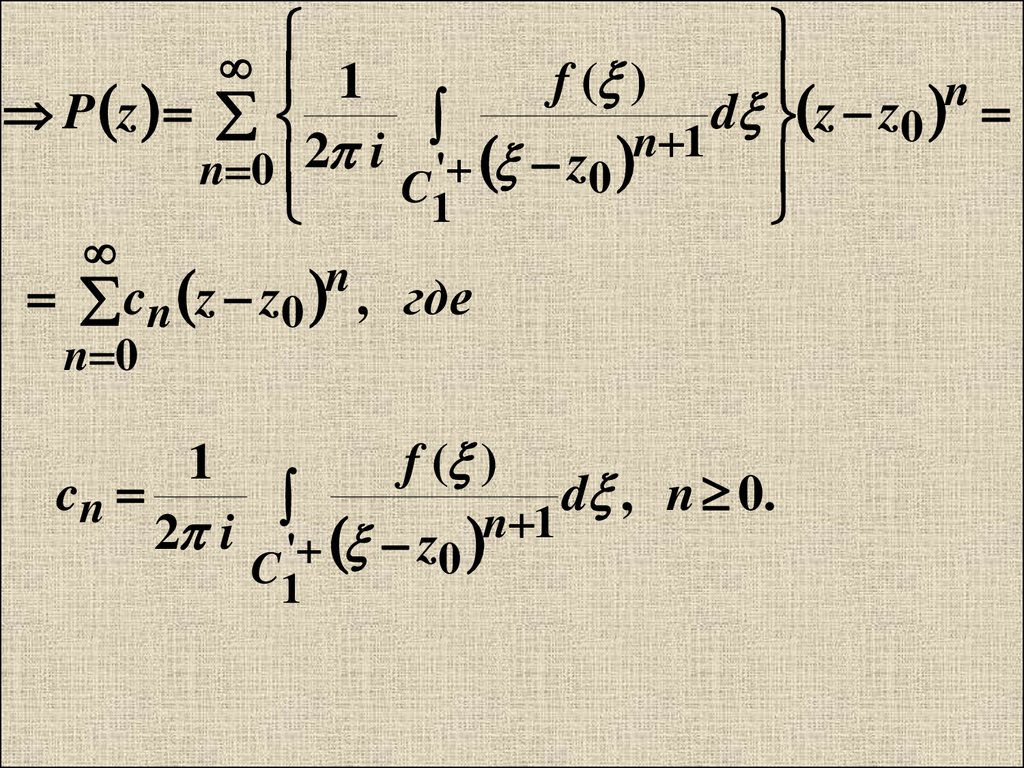
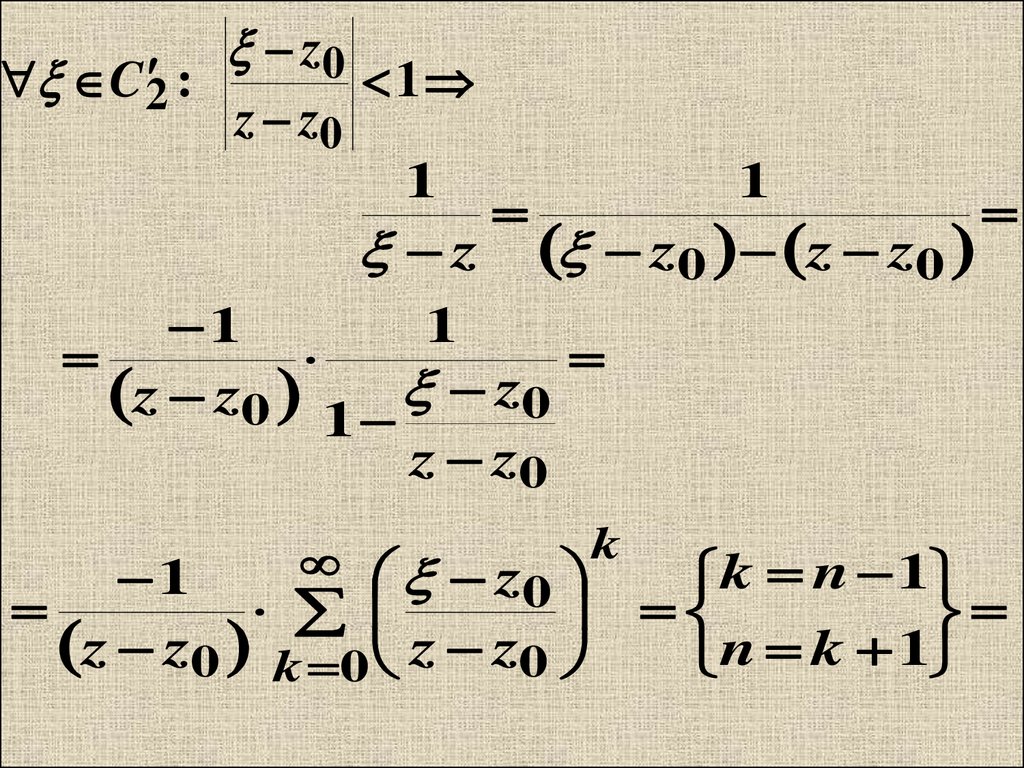
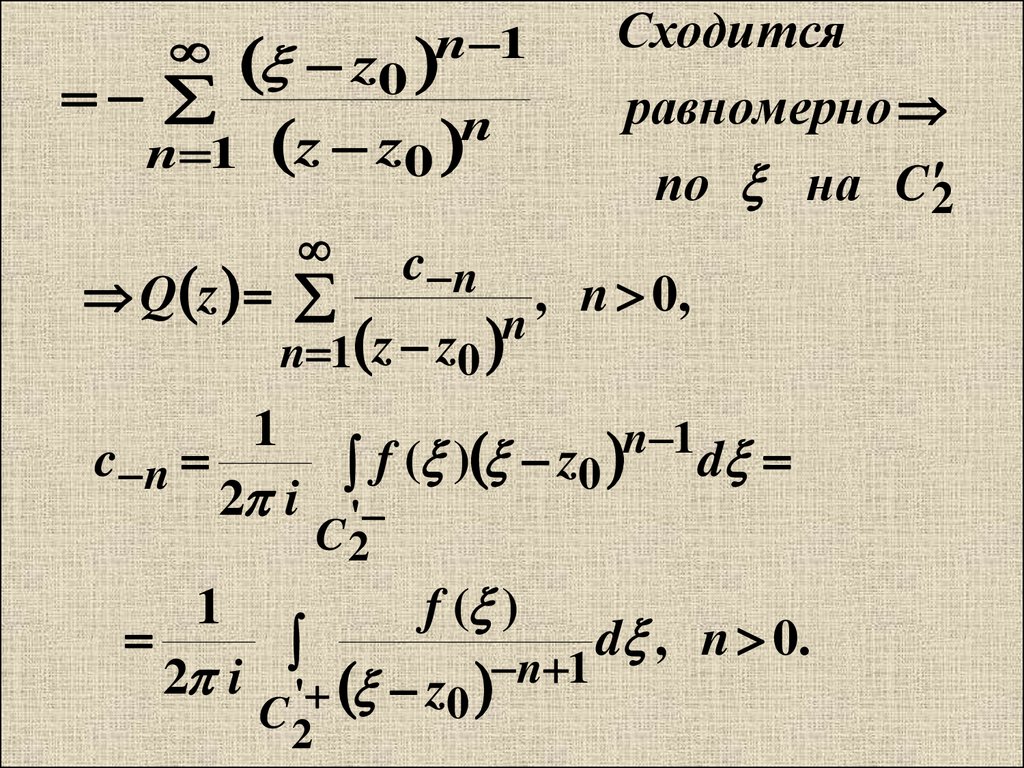

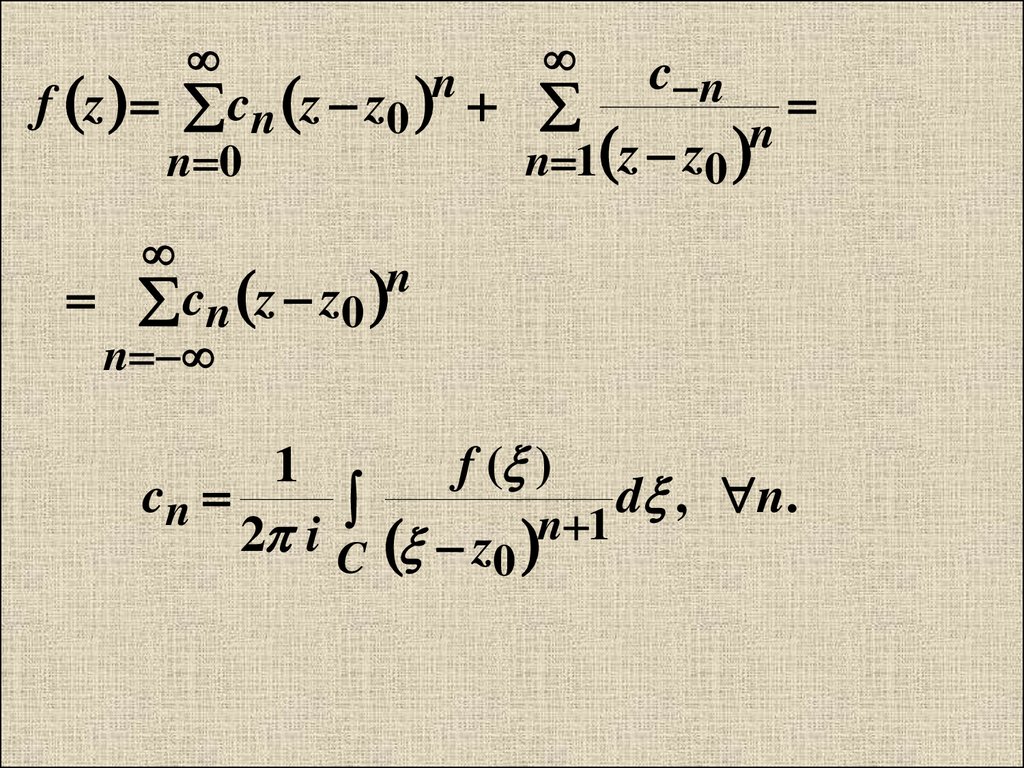
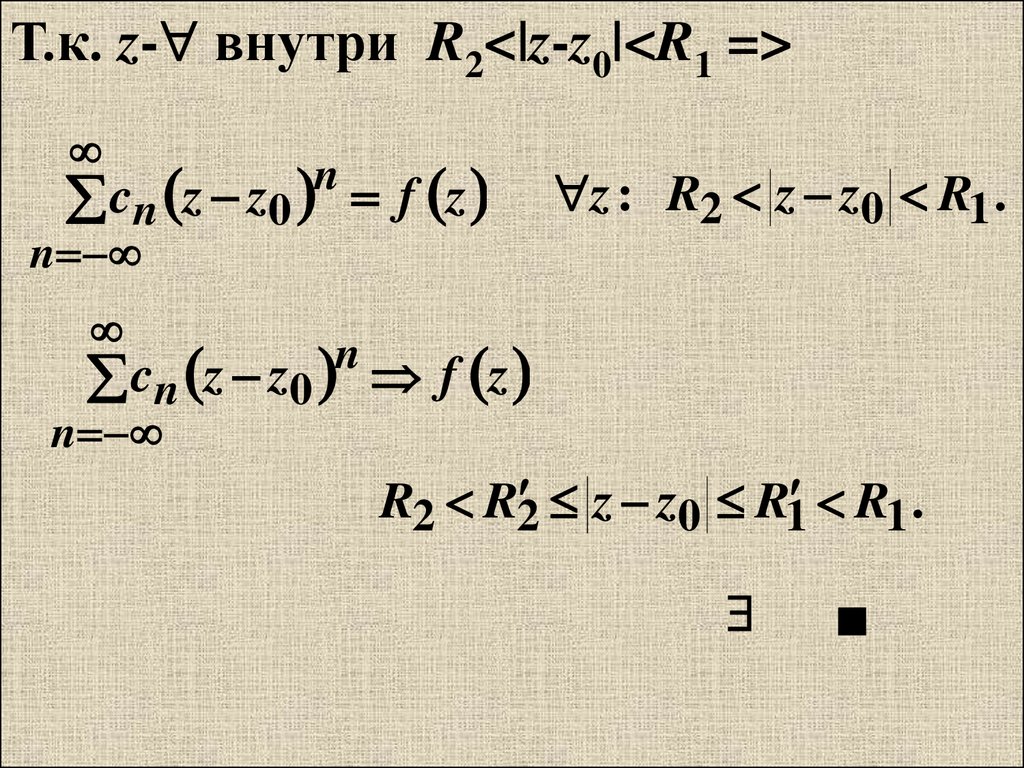
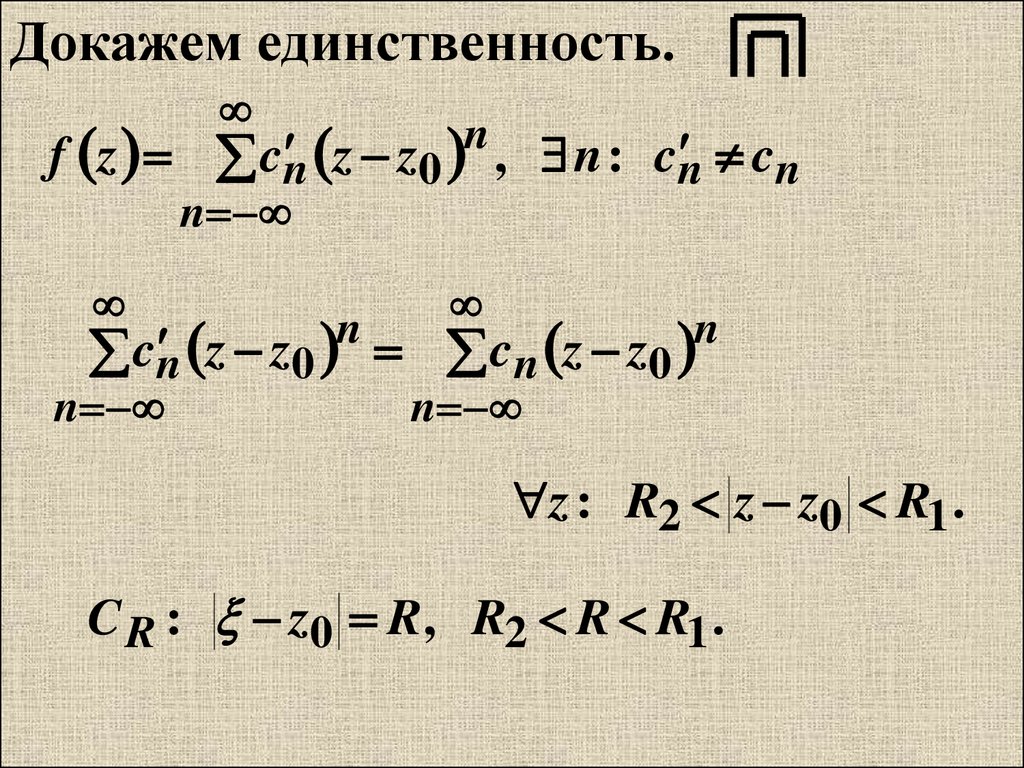
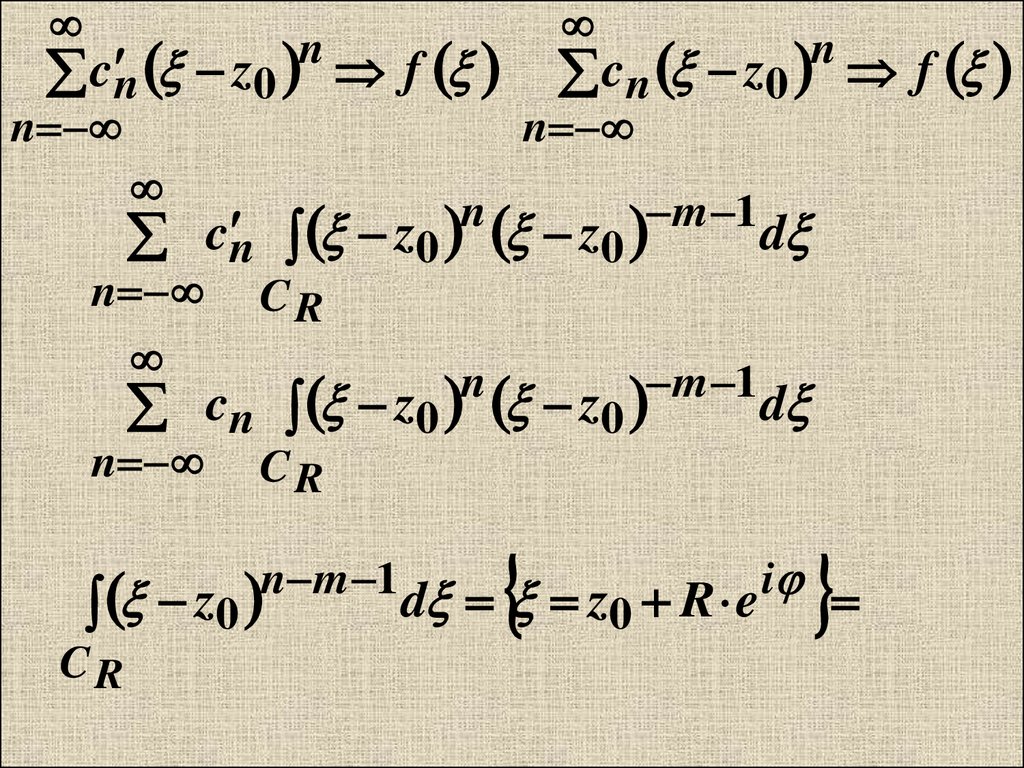

 mathematics
mathematics








