Поверхностные интегралы. Элементы теории поля

1.

Математика 2
Поверхностные интегралы.
Элементы теории поля
Лектор:
доцент отделения математики и информатики
Имас Ольга Николаевна

2.

Теорема. ФОРМУЛА ГРИНА. (связь между двойным интегралом по области D и
криволинейным интегралом по контуру C, ограничивающему область D )
Пусть С – замкнутый контур, ограничивающий область D, D – правильная
область. Пусть во всех точках D заданы непрерывные со своими частными
производными функции P(x,y) и Q(x,y). Тогда
Q( x, y ) P( x, y )
dxdy
P( x, y )d x Q( x, y )d y
x
y
C
D
y
y2(x)
A
D
M
B
a
N
y1(x)
b
x
пропустить 1.5 страницу (Для доказательства (уже доказали) и одного примера)

3.

Независимость интеграла от пути интегрирования
A
N
M
B
пропустить 10 клеточек

4.

Теорема . Пусть P(x,y) и Q(x,y) непрерывны вместе со своими частными
производными в области D.
Тогда для того, чтобы криволинейный интеграла по любому замкнутому
контуру из
D был равен нулю Pd x Qd y 0 ,
C
необходимо и достаточно выполнения равенства P'y( x, y ) = Q'x( x, y )
во всех точках области
D
Pd x Qd y 0
C
пропустить 10 клеточек
P( x, y) Q( x, y)
y
x
∀x,y ∈ D

5.

Теорема . Условие
P( x, y ) Q( x, y )
y
x
равносильно тому, что подынтегральная функция
P(x,y)dx + Q(x,y)dy
есть полный дифференциал некоторой функции
U(x;y)
P(x,y)dx + Q(x,y)dy = dU
пропустить 15 клеточек
∀x,y ∈ D

6.

Определение. Функция U(x,y), градиент которой равен вектору
называется потенциалом этого вектора
F Pi Q j
Теорема .
Криволинейный интеграл от полного дифференциала функции U(x,y) по
любой кривой, соединяющий точки M и N равен разности значений функции
U(x,y) в этих точках.
I
N
Pd x Qd y du( x, y) U ( N ) U ( M )
( MN )
M
Условие полного дифференциала: P'y( x, y ) = Q'x( x, y )
В случае пространственной
Pd x Qd y Rdzy U ( N ) U (M )
( MN )
кривой условие полного дифференциала:
пропустить 1 страницу
P'y= Q'x
P'z= R'x
Q'z= R'y

7.

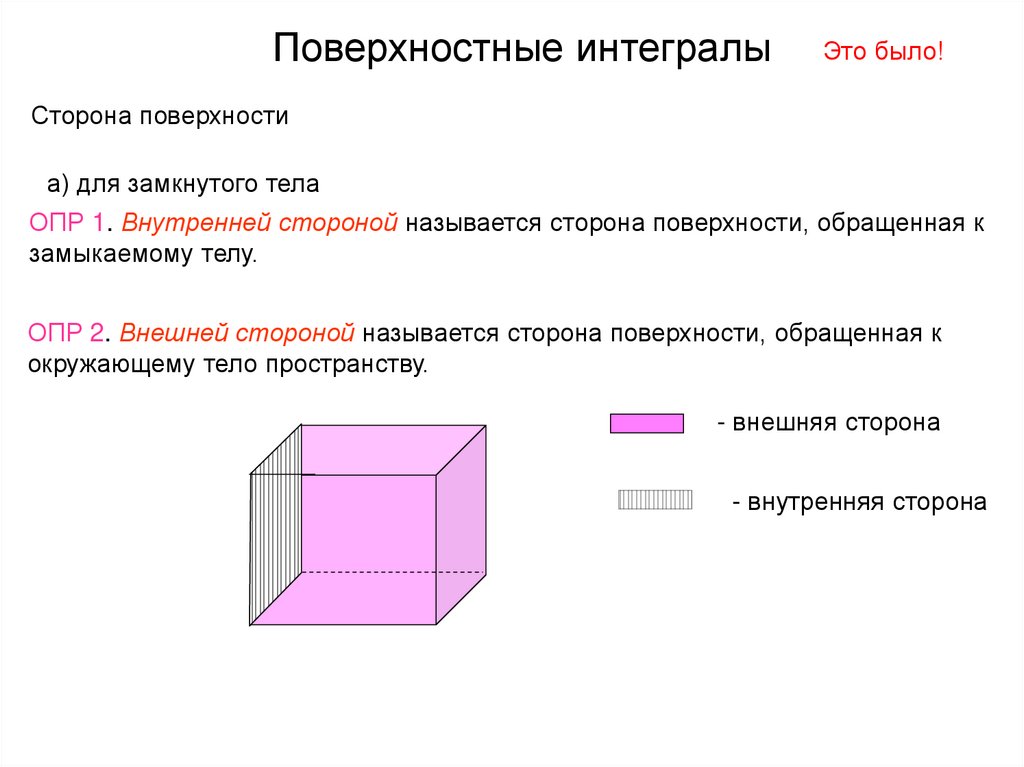
Поверхностные интегралы
Это было!
Сторона поверхности
а) для замкнутого тела
ОПР 1. Внутренней стороной называется сторона поверхности, обращенная к
замыкаемому телу.
ОПР 2. Внешней стороной называется сторона поверхности, обращенная к
окружающему тело пространству.
- внешняя сторона
- внутренняя сторона

8.

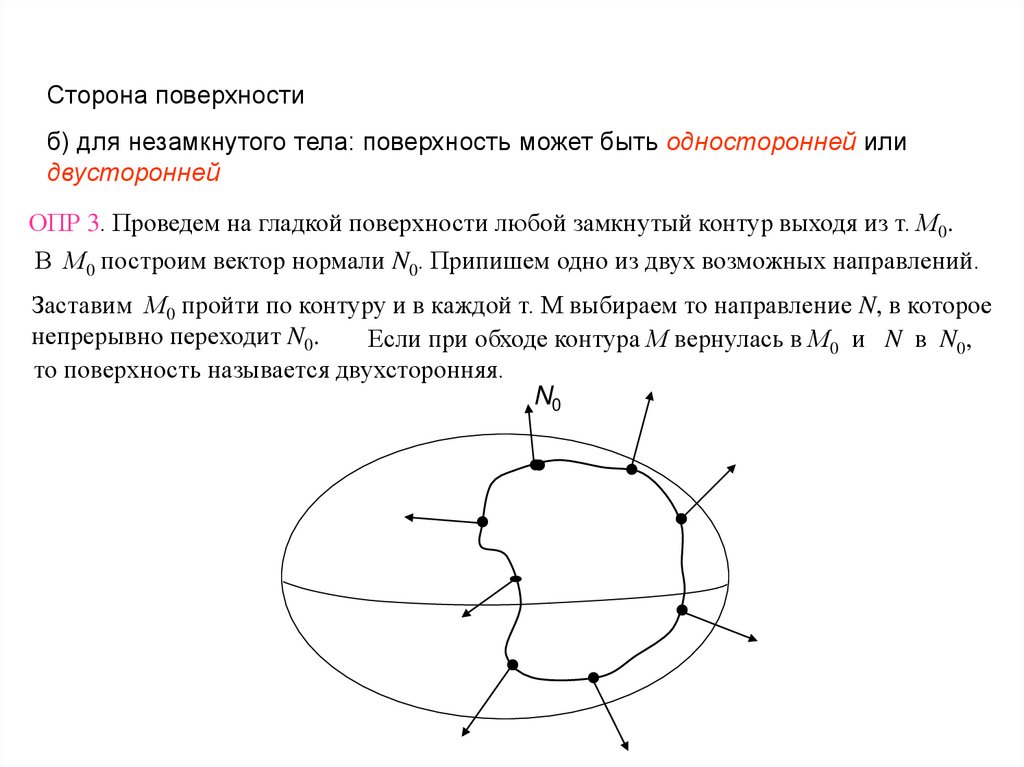
Сторона поверхности
б) для незамкнутого тела: поверхность может быть односторонней или
двусторонней
ОПР 3. Проведем на гладкой поверхности любой замкнутый контур выходя из т. М0.
В М0 построим вектор нормали N0. Припишем одно из двух возможных направлений.
Заставим М0 пройти по контуру и в каждой т. М выбираем то направление N, в которое
непрерывно переходит N0.
Если при обходе контура М вернулась в М0 и N в N0,
то поверхность называется двухсторонняя.
N0

9.

ОПР 4 (поверхностного интеграла 1-го типа).
Пусть дана поверхность s и в каждой ее точке определена функция
f(M) = f(x,y,z).
1) Разобьем поверхность s сетью гладких кривых на n частей:
T ={s1 , s2 , …, sn},
2) выберем точки Mi ∊ si произвольно
n
3) вычислим f(Mi)
( M , T ) f ( M i ) si
4) составим суммы
i 1
имеет конечный предел , не зависящий от
выбора точки Mi и от способа разбиения T, то этот предел называется
Если при d=max si → 0
поверхностным интегралом I типа
f (M )d s lim (M ,T )
d 0
S

10.

Вычисление (сведение к двойному)
g
z
si
sx
N
f(M)
y
x
2
2
f
(
M
)
d
s
f
(
x
,
y
,
z
(
x
,
y
))
1
(
z
)
(
z
)
d xd y
x
y
S
пропустить 20 клеточек
D

11.

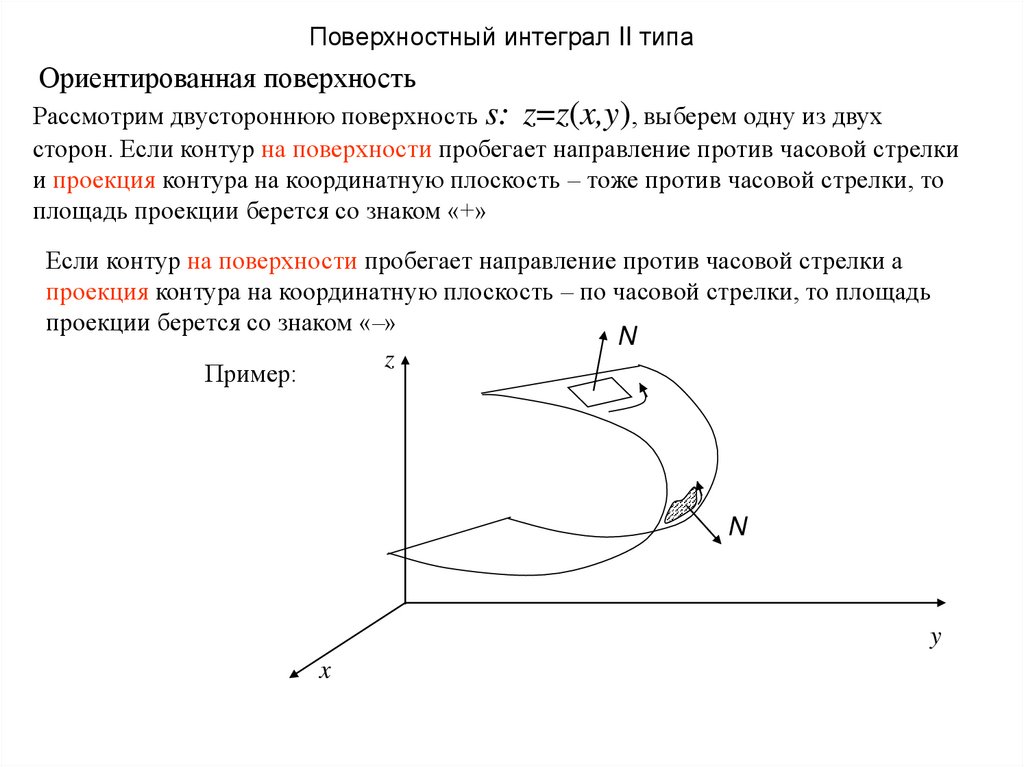
Поверхностный интеграл II типа
Ориентированная поверхность
Рассмотрим двустороннюю поверхность s: z=z(x,y), выберем одну из двух
сторон. Если контур на поверхности пробегает направление против часовой стрелки
и проекция контура на координатную плоскость – тоже против часовой стрелки, то
площадь проекции берется со знаком «+»
Если контур на поверхности пробегает направление против часовой стрелки а
проекция контура на координатную плоскость – по часовой стрелки, то площадь
проекции берется со знаком «–»
N
z
Пример:
N
y
x

12.

ОПР 5 (поверхностного интеграла 2-го типа).
Пусть дана поверхность s и в каждой ее точке определена функция
f(M) = f(x,y,z).
1) Разобьем поверхность s сетью гладких кривых на n частей:
T ={s1 , s2 , …, sn},
2) выберем точки Mi ∊ si произвольно
3) вычислим f(Mi)
n
( M , T ) f ( M i ) Di , где Di – площадь
4) составим сумму
i 1
проекции si на XOY
имеет конечный предел , не зависящий от
выбора точки Mi и от способа разбиения T, то этот предел называется
Если при d=max Di → 0
поверхностным интегралом II типа
n
( M , T ) lim f ( M i ) Di
f ( x, y, z )d xdy dlim
0
d 0
S
i 1

13.

Проецируя si на плоскости
соответственно
f ( x, y, z)d xdz
S
XOZ
и
YOZ
получим интегралы
f ( x, y, z)d ydz
S
В общем случае
P( x, y, z)d ydz Q( x, y, z)d xdz R( x, y, z)d xdy
S
где P(x,y,z), Q(x,y,z), R(x,y,z) – функции, определенные на поверхности s.

14.

Связь между интегралами двух типов
d xdy ds xoy cos g ds
Вспомним:
d xdz ds xoz cos ds
d ydz ds yoz cos ds
пропустить 1.5 страницы