Поверхностные интегралы

1.

2.

Понятие двойного интеграла по плоской области
обобщается на случай интегрирования по
поверхности.
Пусть S – некоторая поверхность, f(x,y,z) –
непрерывная функция на поверхности S.
Разобьем поверхность S на части с площадями
ΔGi. На каждой части выберем точку
M i ( xi , yi , zi )

3.

Сумму вида
n
f ( x , y , z ) G
i 1
i
i
i
i
называют интегральной суммой
для функции f(x,y,z) по поверхности S.

4.

Если
существует
конечный
предел
интегральной суммы при стремлении к
0
диаметра
каждой
площадки
разбиения, не зависящий от способа
разбиения поверхности S и выбора
точек (xi,yi,zi), то он называется
интегралом по поверхности S от
функции f(x,у,z).
n
lim
max G 0
f ( x , y , z ) G f ( x, y, z)dG
i 1
i
i
i
i
S

5.

Свойства поверхностных интегралов аналогичны
свойствам двойных интегралов.
Рассмотрим
вычисление
поверхностных
интегралов.
Пусть дан поверхностный интеграл
f ( x, y, z)dG
S
и поверхность S задана уравнением z=z(x,y).
В этом случае вычисление поверхностного
интеграла сведется к вычислению двойного
интеграла по области D – проекции поверхности
S на плоскость ХОУ.

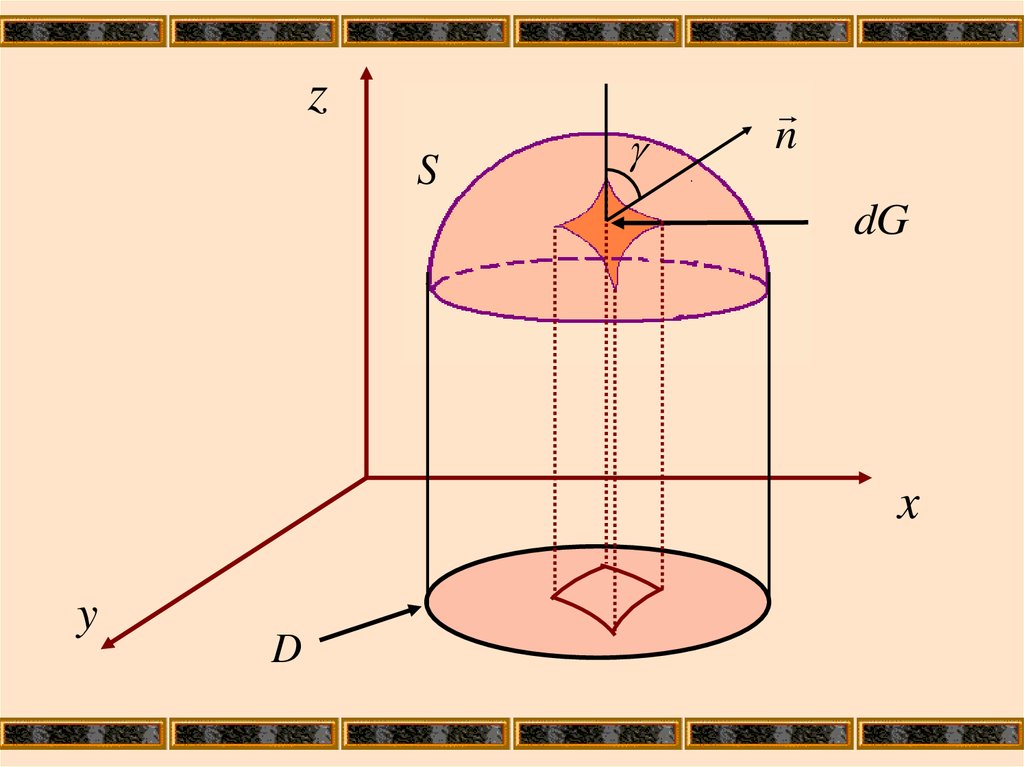
6.

z
S
n
dG
x
y
D

7.

Выберем элемент площади dxdy плоскости D и
проектирующийся в него элемент площади ΔG
поверхности S.
Проведем нормаль к ΔG так, чтобы она
образовывала острый угол γ с oz.
Тогда
dxdy dG cos
Нормаль к поверхности z=z(x,y) имеет проекции
z x , z y , 1
cos
1
1 ( z x ) ( z y )
2
2

8.

Тогда
2
2
dG 1 ( z x ) ( z y ) dxdy
f ( x, y, z )dG
S
D
2
2
f ( x, y, z ( x, y )) 1 ( z x ) ( z y ) dxdy