10.11.2025 Презентация по алгебре и началам анализа на тему_Площадь криволинейной трапеции и интеграл_ (11 класс)(1)

1. Площадь криволинейной трапеции и интеграл.

у
х

2.

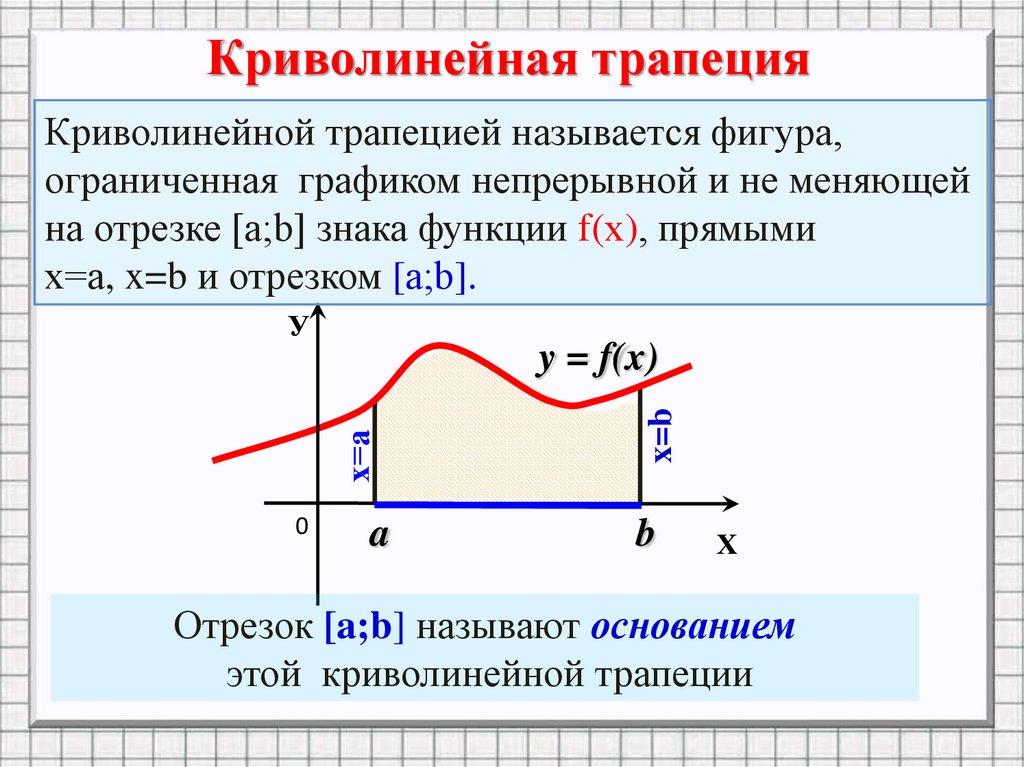
Криволинейная трапеция
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].
У
0
a
x=b
х=а
y = f(x)
b
Х
Отрезок [a;b] называют основанием
этой криволинейной трапеции

3.

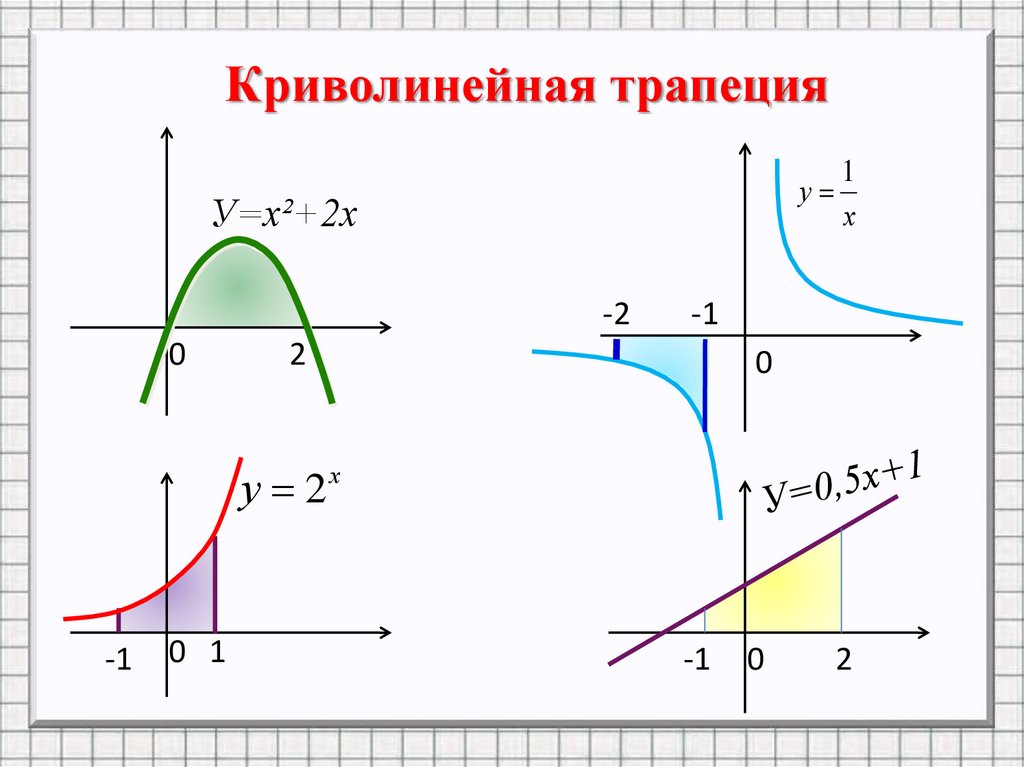
Криволинейная трапеция
у
У=х²+2х
-2
0
-1
0 1
-1
2
у 2
1
х
0
х
-1
0
2

4.

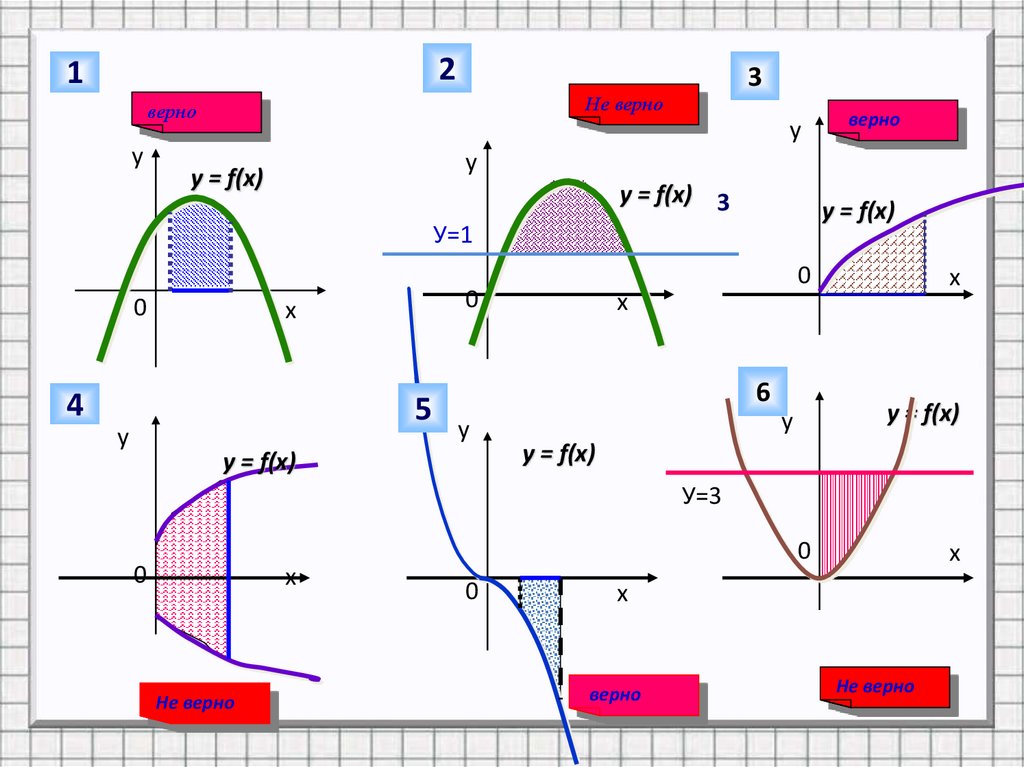
Используя определение ответь на
вопрос:
Какие из заштрихованных на рисунке
фигур являются криволинейными
трапециями, а какие нет?
Заполнить таблицу
№1
№2
№3
№4
№5
№6
Да/нет

5.

2
1
Не верно
верно
у
3
у
у
y = f(x)
y = f(x) 3
y = f(x)
У=1
0
0
0
х
4
5
у
верно
х
6
у
y = f(x)
х
y = f(x)
у
y = f(x)
У=3
0
0
х
Не верно
0
х
х
верно
Не верно

6.

Проверь себя:
№1
да
№2
№3
нет
да
№4
№5
№6
нет
да
нет

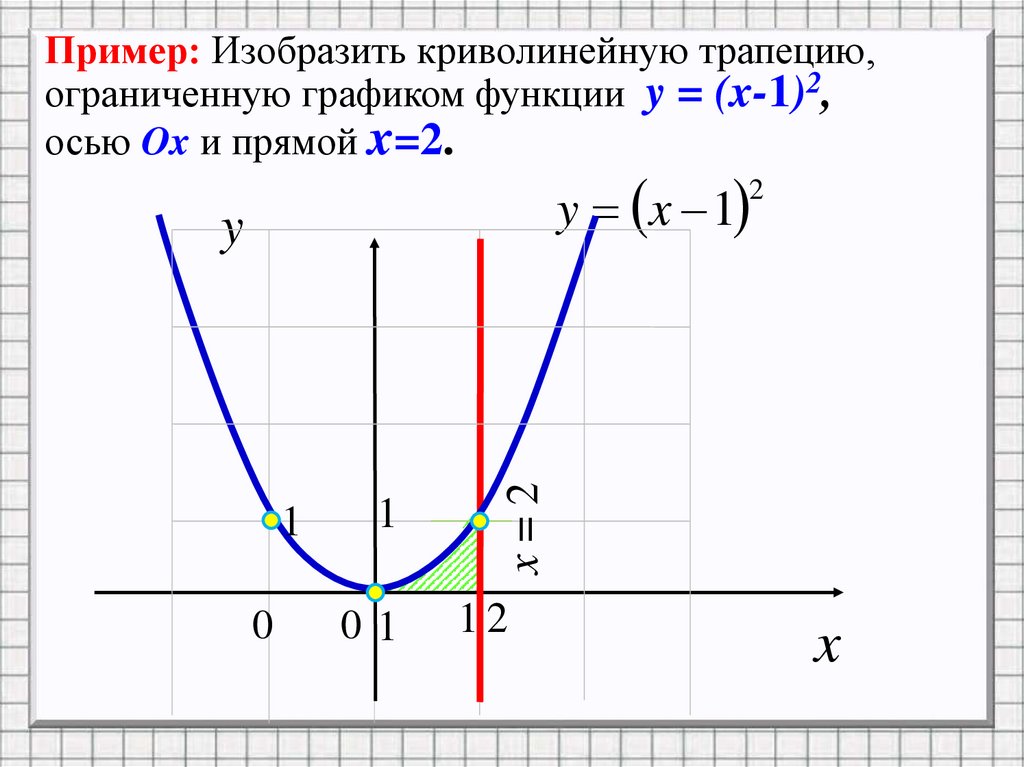
7. Пример: Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью Ox и прямой x=2.

y x 1
2
1
0
1
01
x=2
y
12
x

8.

Площадь криволинейной трапеции можно
вычислить по формуле:
S F (b ) F ( a )
Где F(x) – первообразная функции y=f(x)
Вычисление площади криволинейной трапеции сводится к
отысканию первообразной F(x)
функции f(x), то есть к
интегрированию функции f(x).
Определение
Разность F(b)–F(a) называют интегралом от функции
f(x) на отрезке [a;b] и обозначают:
Верхний предел
интегрирования
Нижний предел
интегрирования
b
f
(
x
)
dx
a
Подынтегральная
функция
Подынтегральное
выражение

9.

Формула Ньютона - Лейбница
b
f ( x)dx F (b) F (a)
a
Таким образом:
Исаак Ньютон
1642-1727
Готфрид Лейбниц
1646-1716 гг.
b
b
a
a
S f ( x)dx F F (b) F (a)

10.

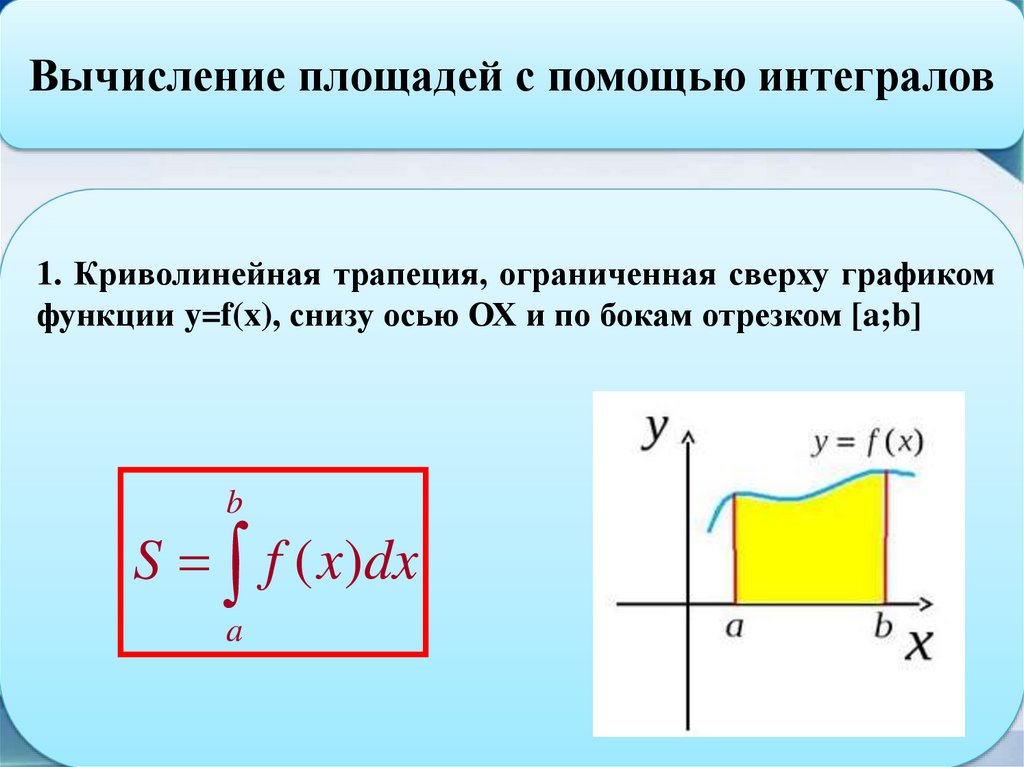
Вычисление площадей с помощью интегралов
1. Криволинейная трапеция, ограниченная сверху графиком
функции y=f(x), снизу осью ОХ и по бокам отрезком [a;b]
b
S f ( x)dx
a

11.

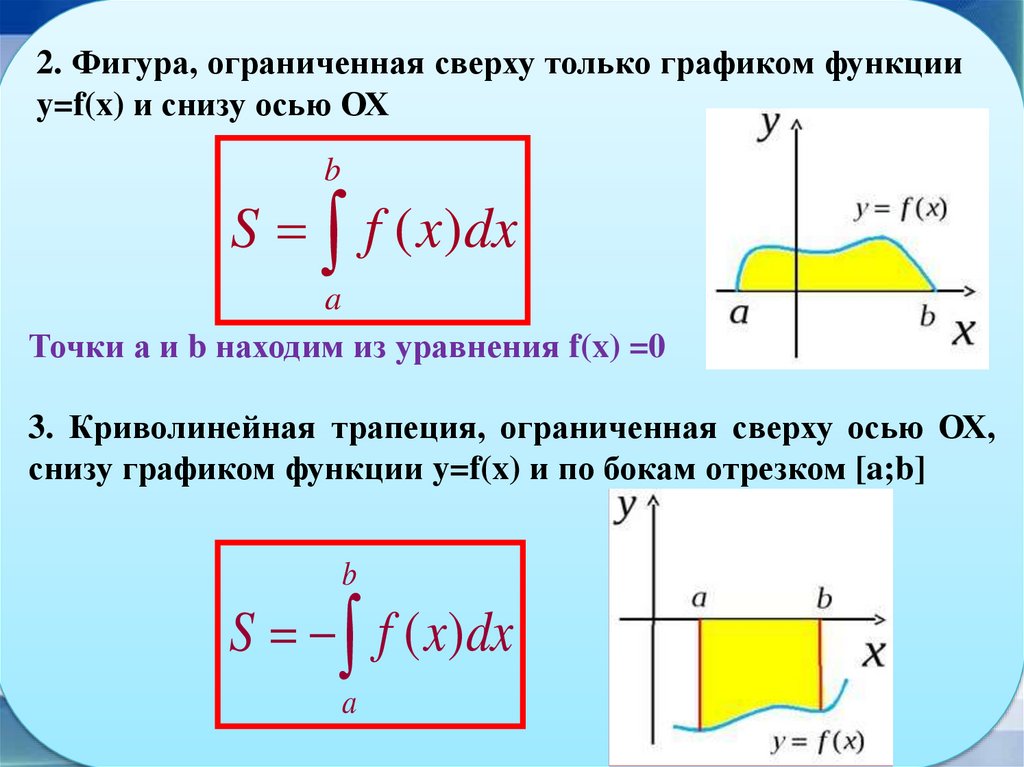
2. Фигура, ограниченная сверху только графиком функции
y=f(x) и снизу осью ОХ
b
S f ( x)dx
a
Точки а и b находим из уравнения f(x) =0
3. Криволинейная трапеция, ограниченная сверху осью ОХ,
снизу графиком функции y=f(x) и по бокам отрезком [a;b]
b
S f ( x)dx
a

12.

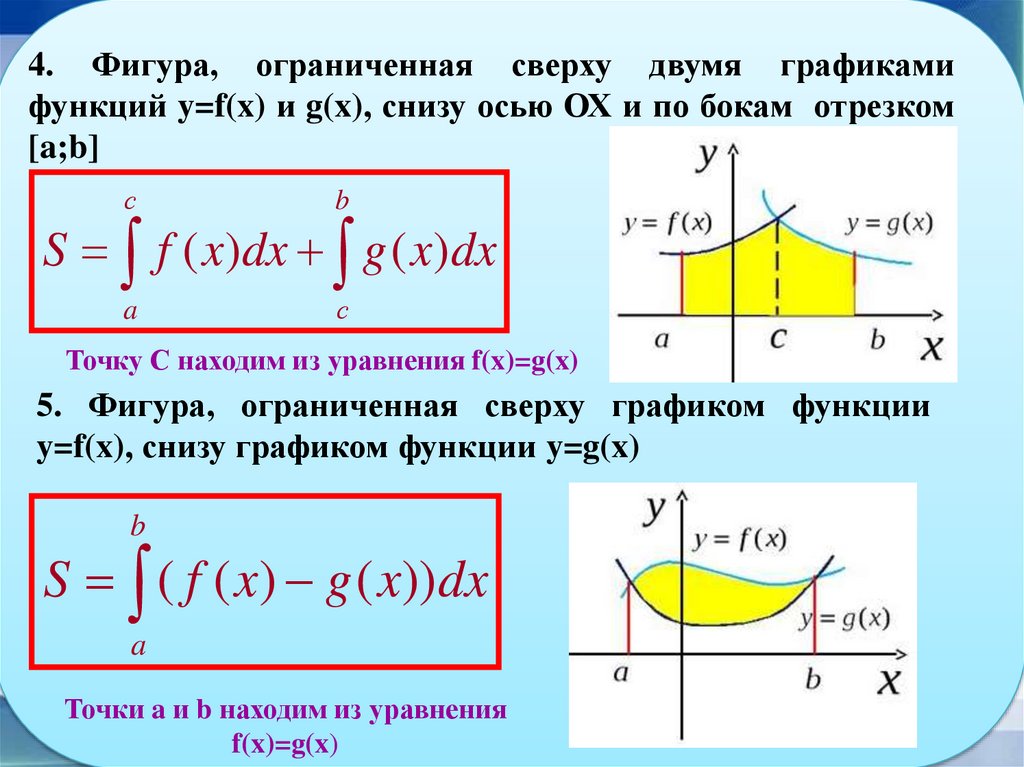
4. Фигура, ограниченная сверху двумя графиками
функций y=f(x) и g(x), снизу осью ОХ и по бокам отрезком
[a;b]
с
b
a
с
S f ( x)dx g ( x)dx
Точку С находим из уравнения f(x)=g(x)
5. Фигура, ограниченная сверху графиком функции
y=f(x), снизу графиком функции y=g(x)
b
S ( f ( x) g ( x)) dx
a
Точки a и b находим из уравнения
f(x)=g(x)

13.

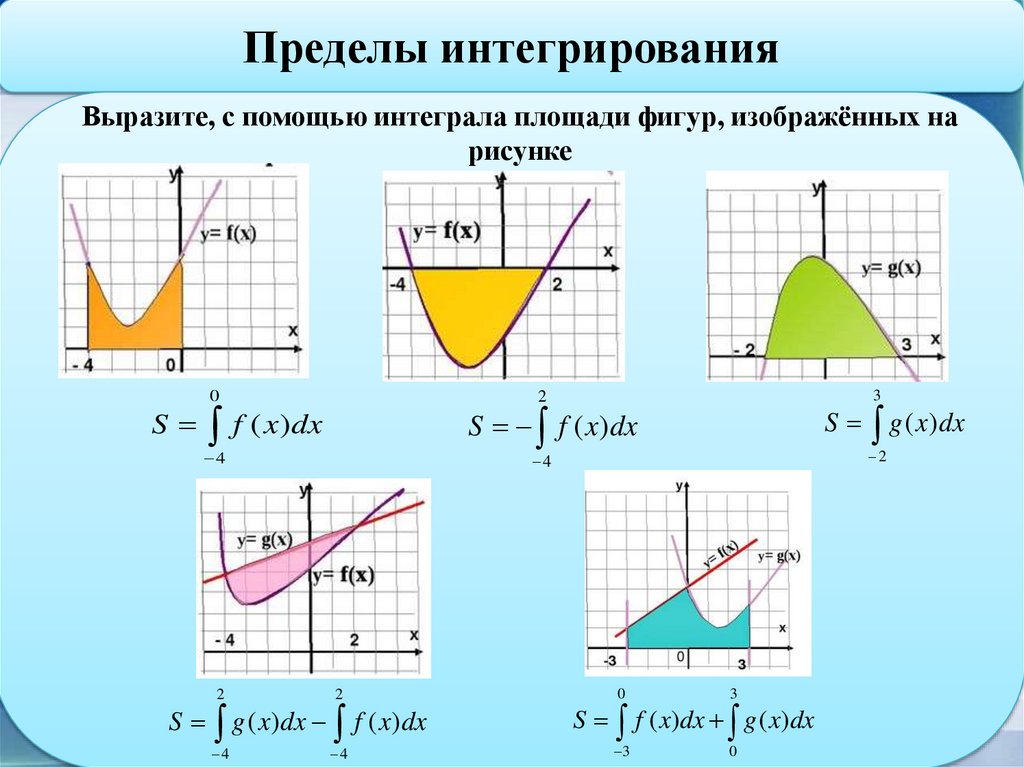
Пределы интегрирования
Выразите, с помощью интеграла площади фигур, изображённых на
рисунке
0
3
2
S f ( x ) dx
S g ( x) dx
S f ( x)dx
4
2
4
2
2
4
4
S g ( x)dx f ( x)dx
0
3
3
0
S f ( x)dx g ( x)dx

14.

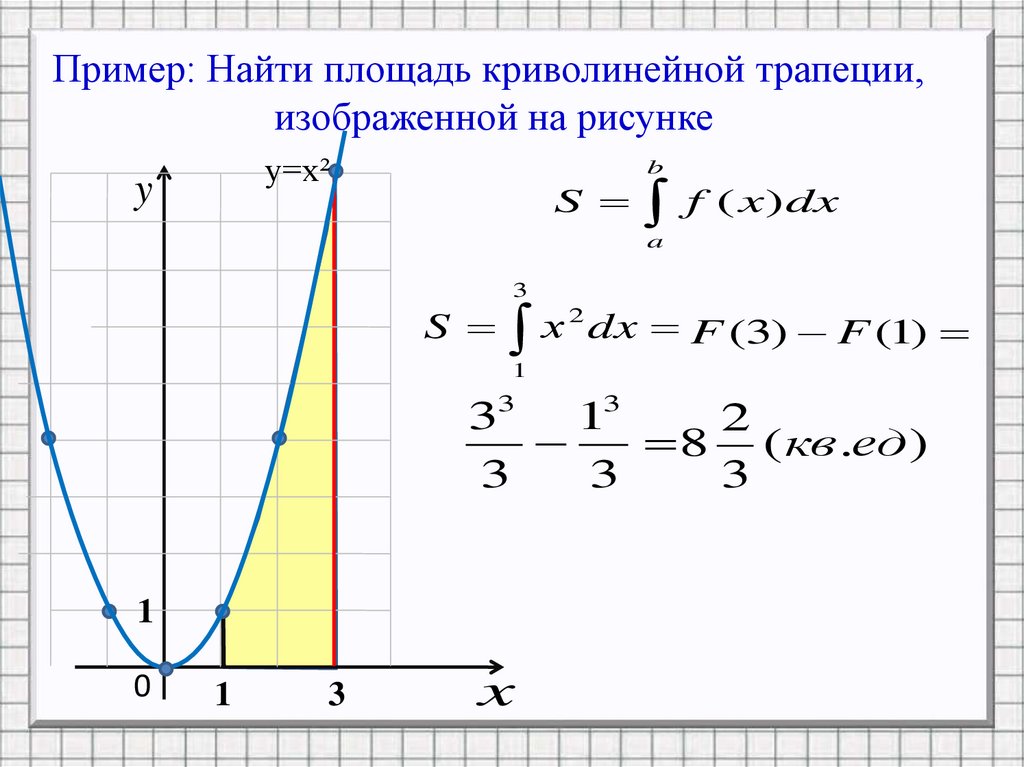
Пример: Найти площадь криволинейной трапеции,
изображенной на рисунке
у=х²
y
b
S f ( x ) dx
a
3
S х 2 dx F (3) F (1)
1
33 13
2
8 ( кв .ед)
3
3
3
1
0
1
3
x

15. Первообразная в ЕГЭ

16. Задание 1