Similar presentations:
1
1. Тема: НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§1. Неопределенный интеграл и егосвойства.
2. Таблица простейших интегралов
1. 0 du C;3. u du
1
u
1
2. 1 du u C;
C , 1;
1
1
4. 2 du C;
u
u
1
6. du ln u C;
u
1
5.
du 2 u C ;
u
u
a
u
7. a du
C;
ln a
9. sin udu cos u C;
10. cos udu sin u C;
1
11.
du tgu C ;
2
cos u
1
12. 2 du ctgu C;
sin u
8. e udu e u C;
3.
11
u
13. 2
du arctg C;
2
u a
a
a
14.
1
u
du arcsin C ;
2
2
a
a u
du
1
u a
15. 2
ln
C;
2
u a
2a u a
16.
du
u2 a 2
ln u u a C .
2
2
4.
Вычисление интегралов с помощьюпреобразования
подынтегрального
выражения к табличной форме и
использования свойств неопределенного
интеграла называется непосредственным
интегрированием.
Вспомогательные сведения
1. a a a
m
n
m n
1
; 3. n a n ;
a
m
2.
a
m n
a ;
n
a
4.
n
a a
m
m
n
.
5. Пример 1. Используя таблицу и свойства интегралов, найти интегралы.
5 1dx
x
5
1. 5 x dx (ô î ðì óëà (3))=
C
x
5 1
1
4 C.
4x
x
x
2. (2 x 7 )dx 2 xdx 7 dx
2
x
x
x
7
7
2
(ô î ðì óëû (3), (7))= 2
C x
C.
2 ln 7
ln 7
6.
3.2
x
dx (ô î ðì óëà (3))=
x dx
5
5
1
2
5
7
x
x 2
=
C
C.
5 1
7
2
2
dx
4. 2
x 16
dx
(ô î ðì óëà (13))= 2
2
x 4
1
x
arctg C .
4
4
7.
5.6.
dx
x 25
2
dx
ln x x 2 25 C .
9 x
2
dx
x
arcsin C .
3
32 x 2
8. 1.3. Основные методы вычисления неопределенных интегралов
Непосредственное интегрированиеМетод интегрирования, при котором
данный интеграл путем тождественных
преобразований подынтегральной функции
(или выражения) и применения свойств
неопределенного интеграла приводится к
одному или нескольким табличным
интегралам, называется непосредственным интегрированием.
9.
При сведении данного интеграла ктабличному часто используется следующее
преобразование дифференциала (операция
«подведения под знак дифференциала»).
f ( u)du d ( f ( u))
Например:
du d (u b), b const;
1
du d (au b), a 0, a const;
a
cos udu d (sin u).
10. Примеры
19
1. (3 x 1) dx (3 x 1) d (3 x 1)
3
10
1 (3 x 1)
C.
3
10
9
dx
1 d (4 x 5)
2.
4x 5 4 4x 5
1
ln 4 x 5 C .
4
11.
xx
x
3. cos 7 dx 5 cos 7 d 7
5
5
5
x
5sin 7 C .
5
12. Интегрирование заменой переменной
Метод замены переменной (методподстановки) состоит в преобразовании
интеграла f(x)dx
в другой интеграл
f(u)du,
который вычисляется проще, чем исходный.
13. Пример
(6x
3)
dx
t 6x 3
dt
dt 6dx , dx
6
6
1 5
1t
t dt
C ( t 6 x 3)
6
66
1.
5
1
6
(6 x 3) C .
36
14.
t 5 7xdx
2.
1
5 7 x dt 7dx , dx dt
7
1 dt
1
ln t C (t 5 7 x )
7 t
7
1
ln 5 7 x C .
7
15.
xt 8,
x
2
3. sin 8 dx
1
2
dt dx , dx 2dt
2
x
2 sin tdt 2cos t C ( t 8)
2
x
2cos 8 C .
2
16. Интегрирование по частям
Формулаudv uv vdu,
где u u( x ) и v v ( x ) – дифференцируемые
функции, называется
формулой интегрирования по частям.
Метод
интегрирования
по
частям
целесообразно применять, если
vdu
более прост в вычислении, чем
udv
.
17. Некоторые типы интегралов, которые можно вычислять методом интегрирования по частям
1. Интегралы вида Pn ( x )e mx dx , Pn ( x )a mx dx,P ( x)sin mxdx, Pn ( x )cos mxdx,
n
где Pn ( x ) − многочлен, m − число.
Здесь полагают u Pn ( x ),
за dv обозначают остальные сомножители.
18.
2. Интегралы вида Pn ( x )ln xdx, Pn ( x )arcsin xdx,P ( x)arccos xdx, P ( x)arctgxdx, P ( x)arcctgxdx.
n
n
n
Pn ( x )dx dv
Здесь полагают
за u обозначают остальные сомножители.
3. Интегралы вида e ax cos bxdx, e ax sin bxdx ,
где a и b − числа.
ax
За u можно принять функцию e .
19. Пример. Вычислить неопределенные интегралы методом интегрирования по частям.
1. 2 x 5 cos xdxu 2 x 5, du 2dx
dv cos x , v cos xdx sin x
(2 x 5) sin x 2 sin xdx
(2 x 5)sin x 2cos x C


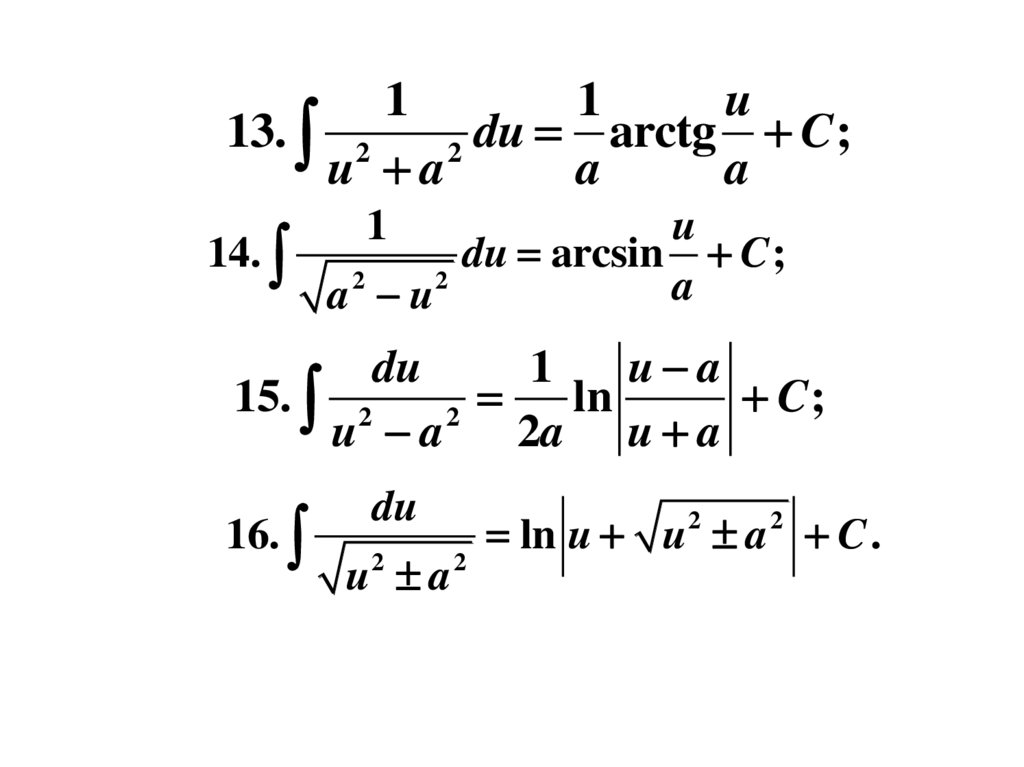


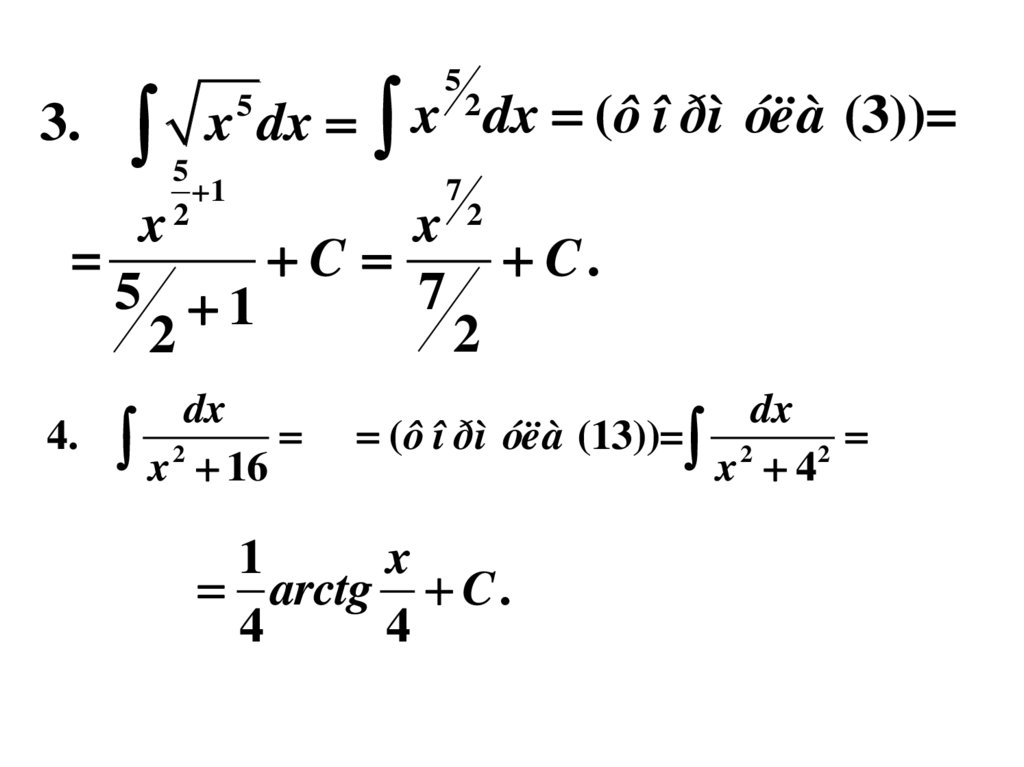
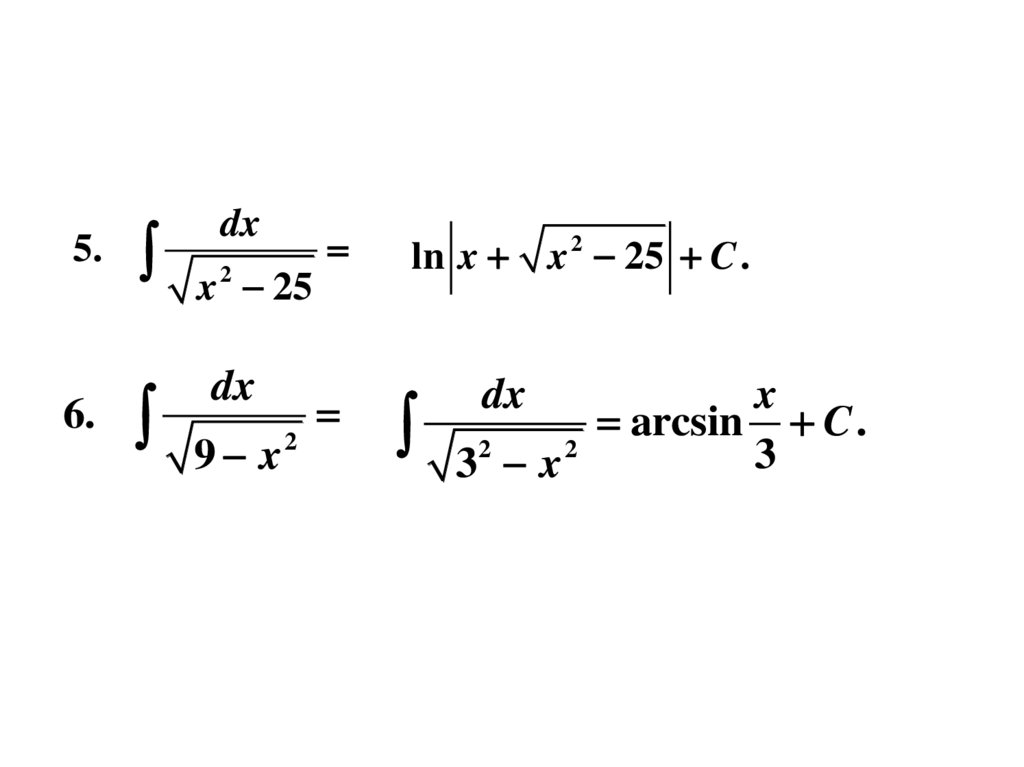


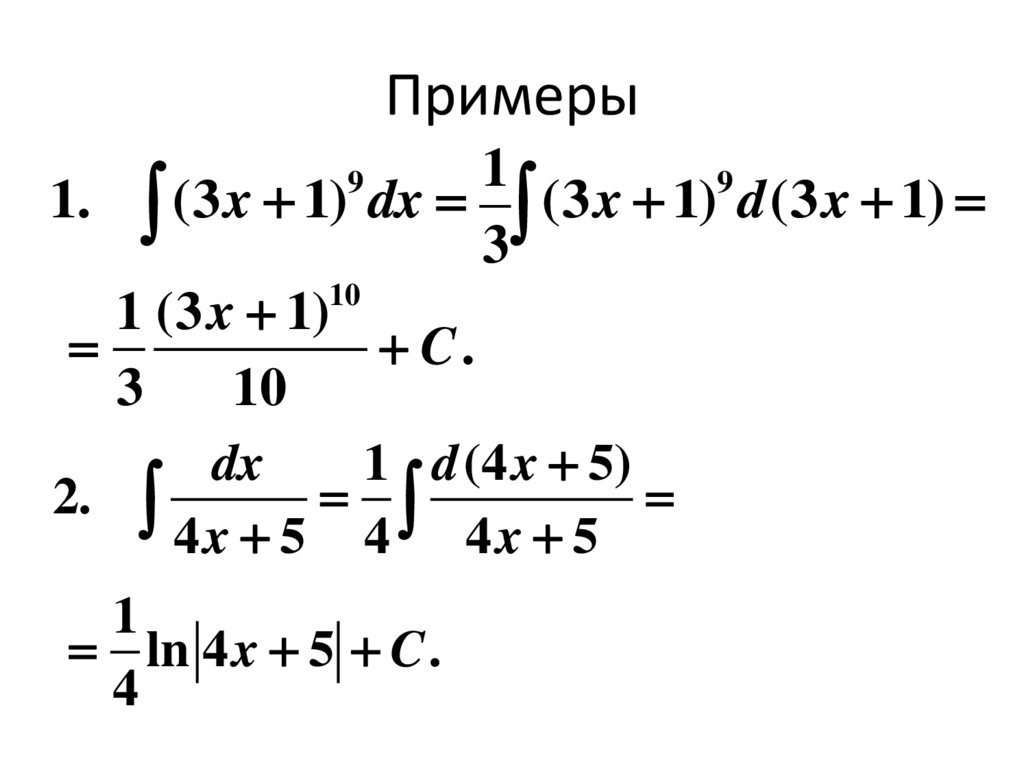
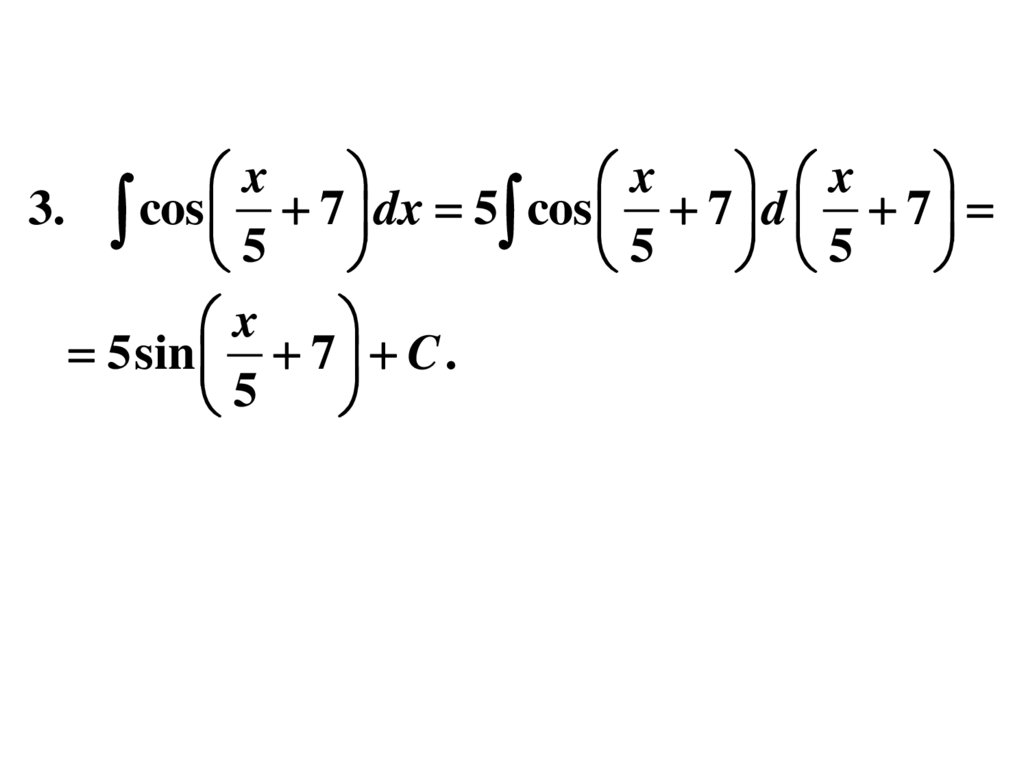

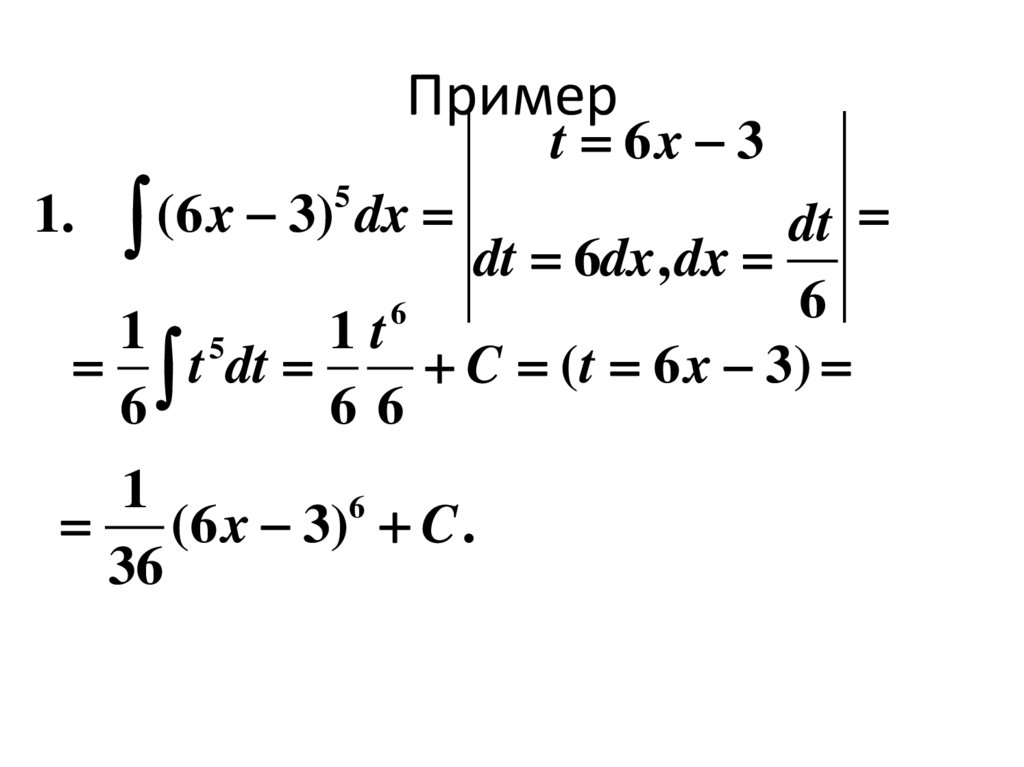
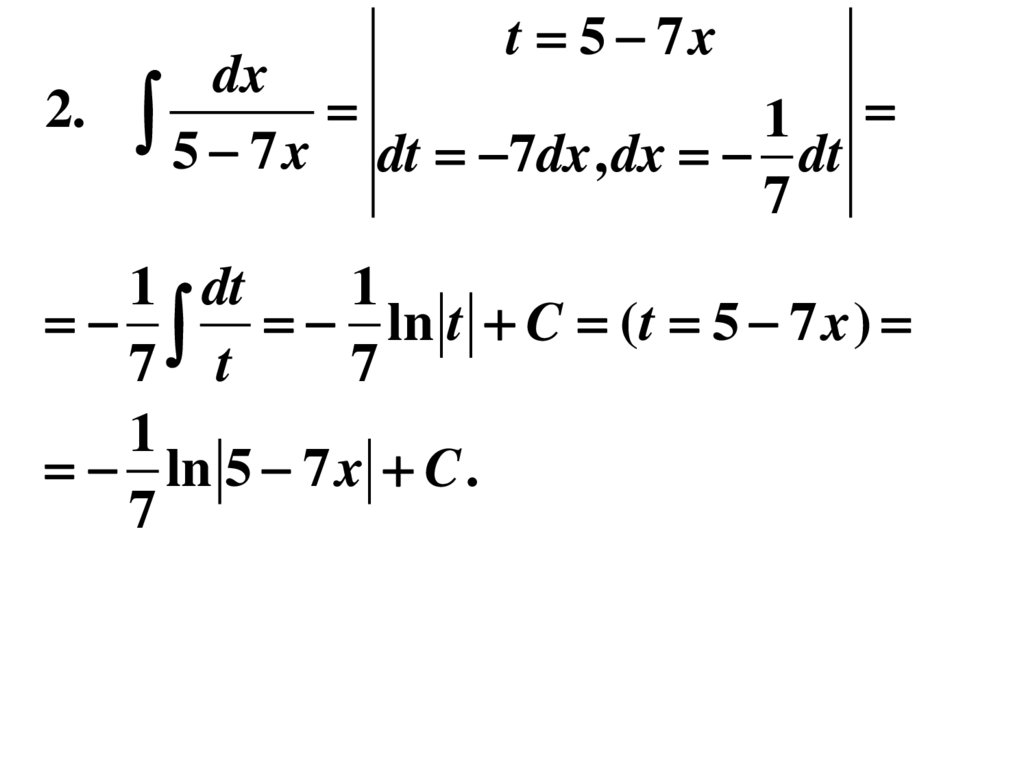
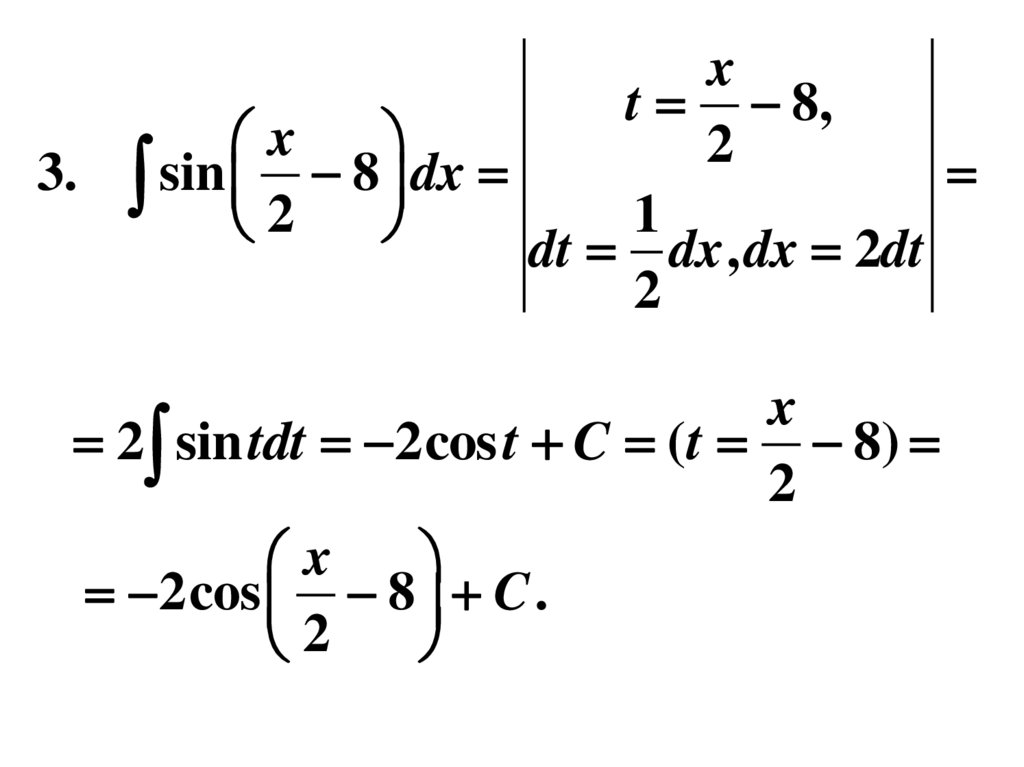




 mathematics
mathematics








