Similar presentations:
Жазықтықтың теңдеуі
1. Жазықтықтың теңдеуі
2. Оқу мақсаты:
11.3.4.3 кеңістіктегі жазықтықтың теңдеуінқұрастыру.
Сабақ мақсаты:
• Жазықтықтың жалпы теңдеуін,
• жазықтықтың кесінділік теңдеуін,
• үш нүкте арқылы өтетін жазықтықтың
теңдеуін құра білу.
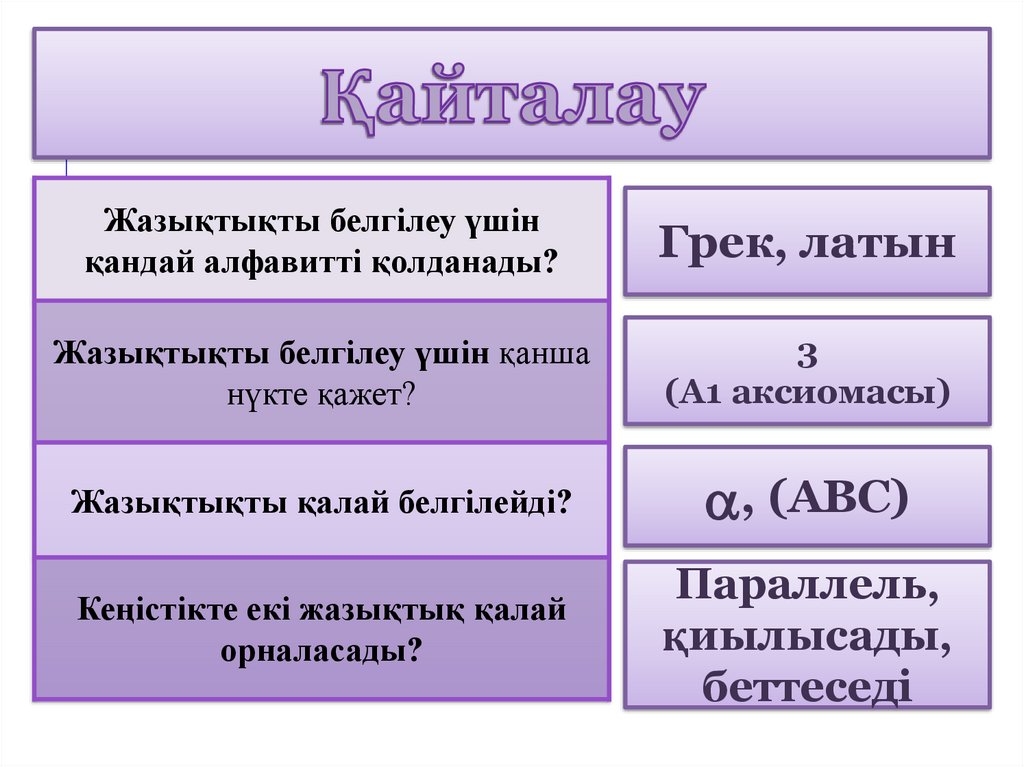
3. Қайталау
Жазықтықты белгілеу үшінқандай алфавитті қолданады?
Грек, латын
Жазықтықты белгілеу үшін қанша
нүкте қажет?
3
(А1 аксиомасы)
Жазықтықты қалай белгілейді?
, (ABC)
Кеңістікте екі жазықтық қалай
орналасады?
Параллель,
қиылысады,
беттеседі
4.
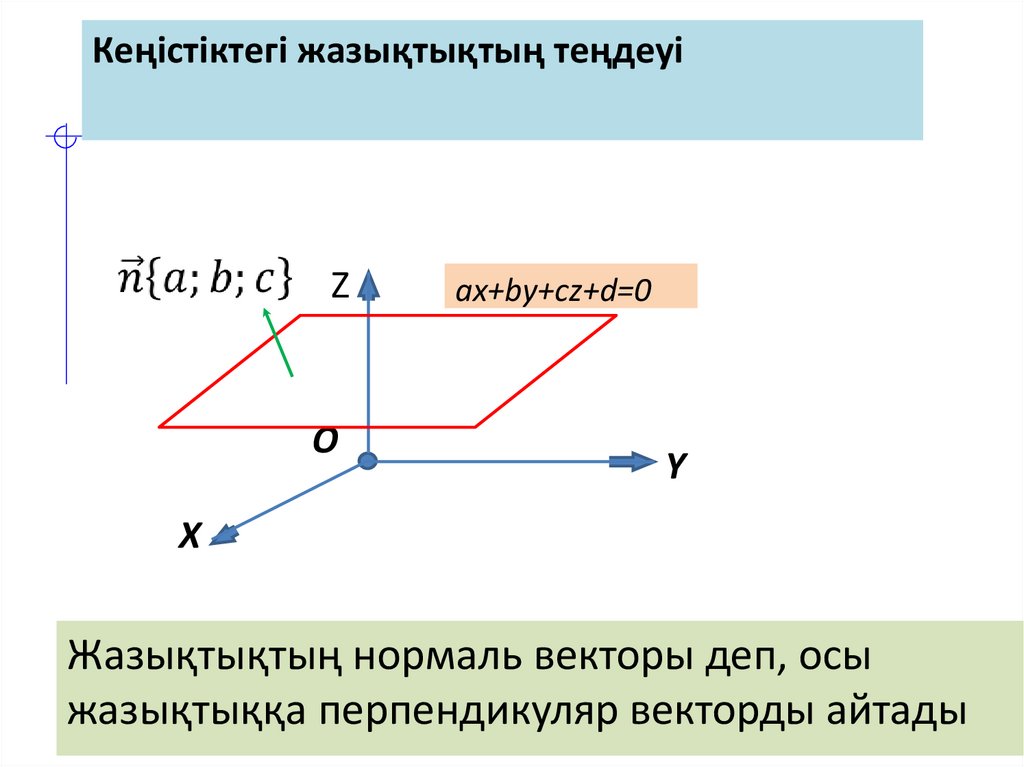
Кеңістіктегі жазықтықтың теңдеуіZ
О
ax+by+cz+d=0
Y
X
Жазықтықтың нормаль векторы деп, осы
жазықтыққа перпендикуляр векторды айтады
5.
Берілген векторға перпендикуляр және берілгеннүкте арқылы өтетін жазықтық теңдеуі
Жазықтықтың нормаль векторы
мұндағы,
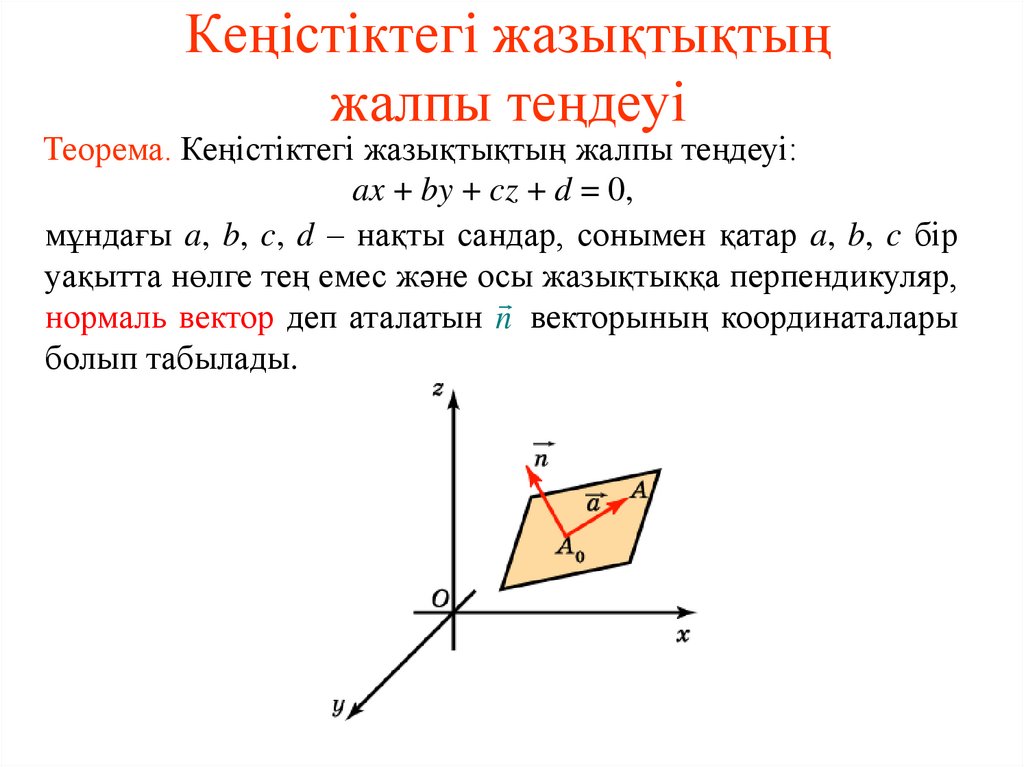
6. Кеңістіктегі жазықтықтың жалпы теңдеуі
Теорема. Кеңістіктегі жазықтықтың жалпы теңдеуі:ax + by + cz + d = 0,
мұндағы a, b, c, d – нақты сандар, сонымен қатар a, b, c бір
уақытта нөлге тең емес және осы жазықтыққа перпендикуляр,
нормаль вектор деп аталатын n векторының координаталары
болып табылады.
7. Мысал 1. нүктесі және векторына перпендикуляр болатын жазықтықтың теңдеуін жазыңыз.
8. Жазықтықтың жалпы теңдеуі
Толық емес теңдеу түрлері:1) D 0;
Жазықтық О нүктесі арқылы
өтеді.
2) A 0;
Ax By Cz 0
By Cz D 0 ll (OX )
3) B 0;
Ax Cz D 0
4) C 0;
Ax By D 0 ll (OZ )
z
ll (OY )
5) A 0; B 0
Cz D 0 ll ( XOY )
6) B 0; C 0 Ax D 0 ll (YOZ )
7) A 0; C 0
0
By D 0 ll ( XOZ ) x
8) B 0; C 0; D 0
Ax 0 x 0
9) A 0; C 0; D 0
By 0 y 0
Cz 0 z 0
10) A 0; B 0; D 0
(YOZ )
( XOZ )
( XOY )
y
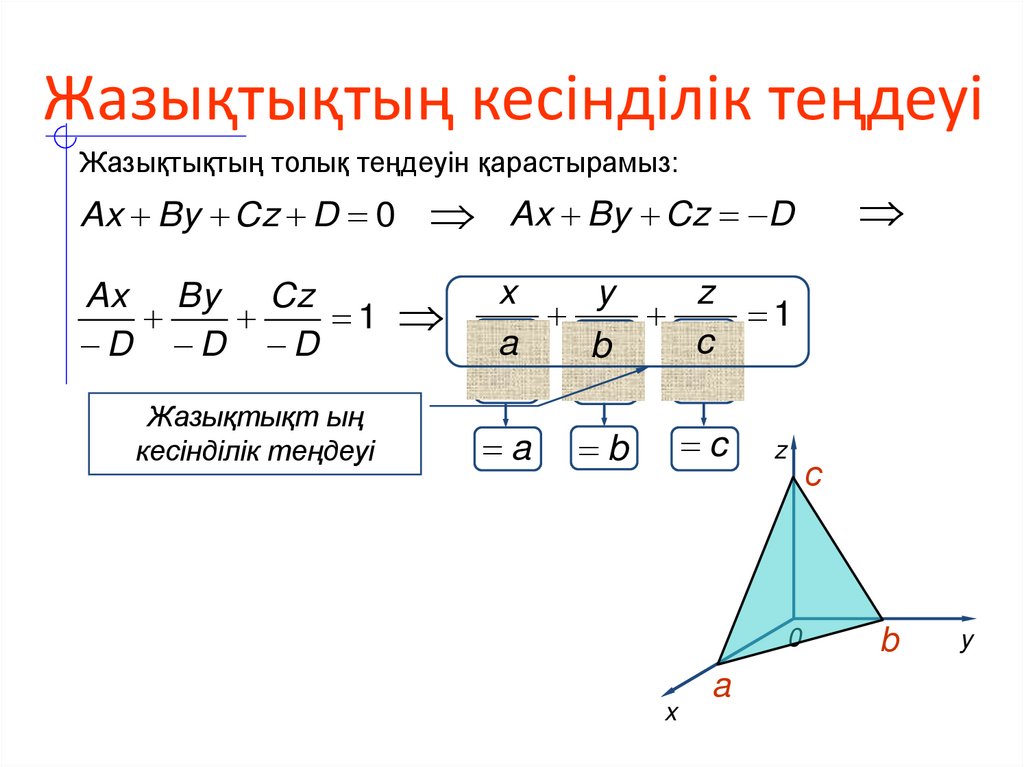
9. Жазықтықтың кесінділік теңдеуі
Жазықтықтың толық теңдеуін қарастырамыз:Ax By Cz D 0
Ax By Cz
1
D D D
Жазықтықт ың
кесінділік теңдеуі
Ax By Cz D
x
y
z
1
aD bD cD
A
B
C
a
c
b
z
с
0
x
a
b
y
10. Мысал 2.
11. Үш нүкте арқылы өтетін жазықтықтың теңдеуі
12. Мысал 3
ABCD тетраэдердің А нүктесінен түсірілген биіктігін табыңыз;Төбелерінің координаталары: A(1; 1; 1), B(0; 2; 5), C(3; -1; 4), D(4; 2 ; 1)
BCD жазықтығының теңдеуі:
x 0
y 2
A
z 5
3 0 1 2 4 5 0
4 0
2 2
x
y 2 z 5
3
3
4
0
1 5
h
B
3 1
1 0 x
0
4
4
12x 8 y 2 12( z 5) 0
y 2
3
D
1
4 4
С
( z 5)
3 3
4
0
3x 2 y 3 z 19 0
0








 mathematics
mathematics








