7_тақырып_Кеңістіктегі_түзудің_теңдеулері_Екі_түзудің_арасындағы

1. Аналитикалық геометрия және сызықтық алгебра

Қазақстан Республикасының Білім және ғылым министрлігі
Қарағанды Бөкетов университеті
Математика және ақпараттық технологиялар факультеті
Тақырыбы: Кеңістіктегі түзудің теңдеулері. Екі түзудің арасындағы бұрыш
«6В05304-Физика» білім беру бағдарламасы
Авторлар:
Медеубаев Н.Қ., проф. Т.Ғ.Мұстафин атындағы алгебра, мат. логика және геометрия
кафедрасының аға оқытушысы, РһD.
Оразбекова Р.Т., проф. Т.Ғ.Мұстафин атындағы алгебра, мат. логика және геометрия
кафедрасының аға оқытушысы, математика магистры.
Сабақ түрі: дәріс
Қарағанды 2022

2. Кеңістіктегі түзулер

Кеңістікте қандай да болмасын d түзуі
берілсін. М0 осы түзуге тиісті болсын. М0 ∈ d,
l ∥d болады, l ≠0. Осындай 0-ден өзгеше, түзуге
параллель векторды, осы түзудің бағыттаушы
векторы деп атайды.
M
О

3.

Вектордың координаталарын орнына қойсақ, мына теңдеуді аламыз.
(2)
(2) теңдеу түзудің параметрлік теңдеуі деп аталады.
Осы (2) теңдеуде ̅l бағыттаушы векторының координаталары 0-ге тең болмаса, яғни l₁,l₂, l₃≠0, онда
бұл теңдеуден t параметрінен құтылуға болады.
(3)
(3) теңдеу түзудің канондық теңдеуі деп аталады.

4.

(4)
(4) теңдеу екі нүкте арқылы өтетін түзудің теңдеуі.

5. Түзудің екі жазықтықтың қиылысуы сызығы ретінде берілуі

(5)
Осы түзудің бағыттаушы векторын табу үшін, берілген жазықтықтардың нормаль векторларын тауып,
оларды векторлық түрде көбейтеміз.
(6)
(6) теңдеу d түзуінің бағыттаушы векторы деп аталады.

6. Кеңістіктегі екі түзудің арасындағы бұрыш. Екі түзудің перпендикулярлық және параллельдік шарттары

Екі түзу берілген:
Осы екі түзудің арасындағы бұрышты табайық.
(7)

7.

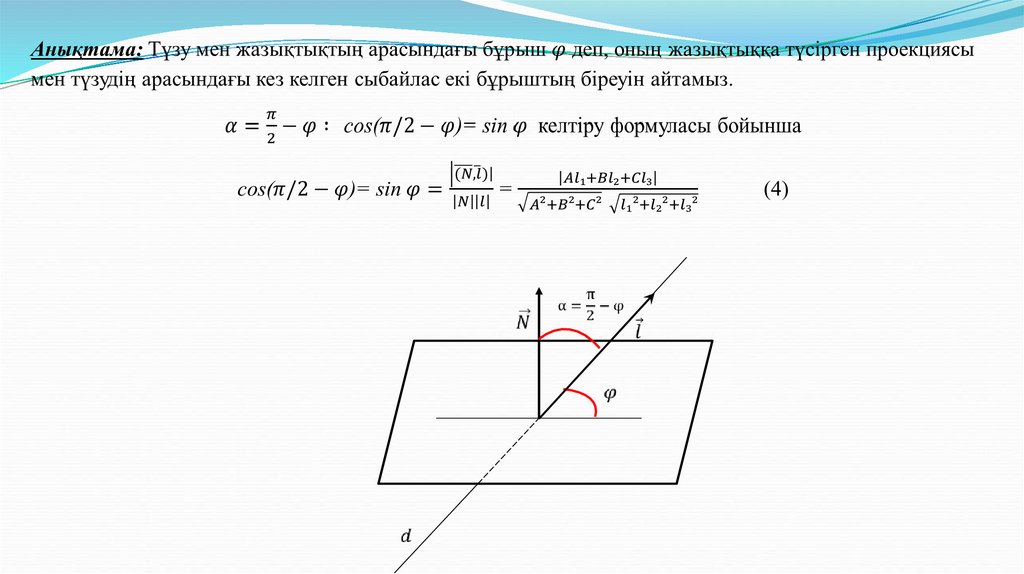
(8)

8. Түзу мен жазықтықтың өзара орналасуы. Түзу мен жазықтықтың арасындағы бұрыш.

(1)

9.

(2)

10.

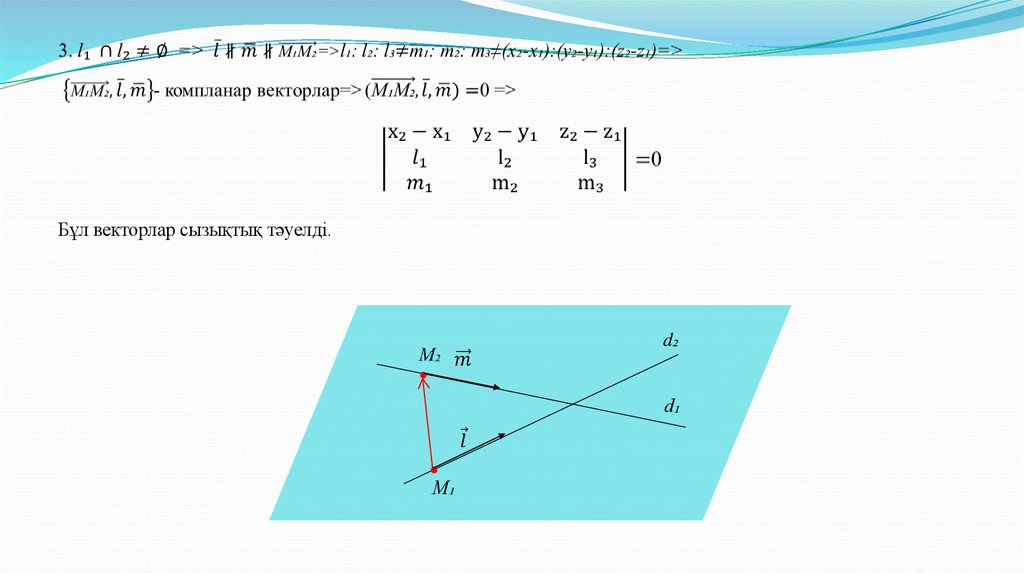
11. Кеңістіктегі екі түзудің өзара орналасуы.

12.

d₂
d₁

13.

Бұл векторлар сызықтық тәуелді.
d₂
d₁

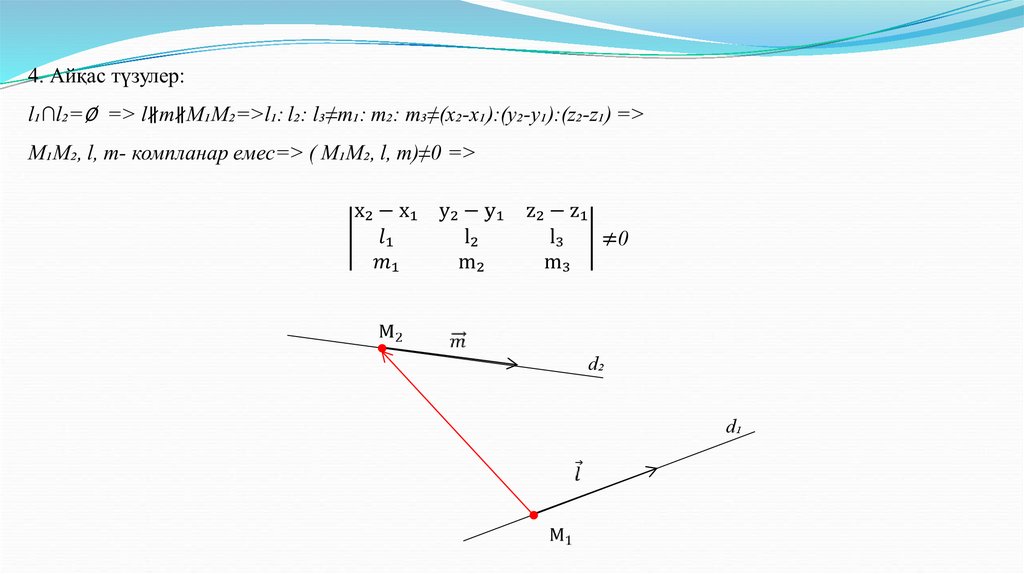
14.

d₂
d₁

15.

1-мысал.
2 x y z 1 0
3x y 2 z 3 0
2-мысал.
x 1 y
z 3
x y 2 z
және
түзулерінің арасындағы бұрышты табу керек.
1
4
1
2
2
1

16.

3-мысал.
x 1 y 2 z 3
түзуі мен
3
m
2
x 3 y 6 z 7 0 жазықтығының параллель болғандағы
m -нің
мәнін табу керек.
Шешуі: Түзу мен жазықтық параллель болса, онда олардың бағыттаушы векторы мен нормал векторы
перпендикуляр болуы керек. Осыдан олардың скаляр көбейтіндісі 0-ге тең болады.
4-мысал.
x 2 y 2 z 1
түзуі мен 2 x 3 y 3z 8 0 жазықтығының қиылысу нүктесін табу керек.
3
1
2
Шешуі: Түзу мен жазықтықтың қиылысу нүктесін табу үшін олардың теңдеулерін біріктіріп шешеміз.
Яғни, түзудің теңдеуін параметрлік түрге келтіріп, x,у,z-тің мәндерін тауып , оларды жазықтықтың
теңдеуіне қойып t-ның мәнін анықтаймыз.
х+2=3t; y-2= - t; z+1=2t ⇒ х=3t-2; у=2- t; z=2t-1
2(3t-2)+3(2 - t)+3(2t -1)-8=0
6t-4+6-3t+6t-3-8=0
9t=9 ⇒ t=1.
х=1;у=1; z=1.

17. Назарларыңызға рақмет!