Similar presentations:
Векторная алгебра_1
1. Раздел 2. Векторная алгебра
§ 1. Определение вектора.Координаты вектора
2. 1.1. Основные определения
Определение 1. Вектором a называетсянаправленный отрезок.
У вектора AB точка А называется
началом вектора AB , точка В – его концом.
3.
Определение 2.Вектор нулевой
нуль-вектором.
длины
называется
4.
Определение 3.a
b
Два
вектора
и
называются
коллинеарными, если они расположены на
параллельных прямых или на одной прямой.
5.
Определение 4.Три
вектора
называются
компланарными, если они лежат в одной
плоскости.
Определение 5.
Длиной вектора называется расстояние
между началом вектора и его концом.
Обозначение: a
6.
Определение 6.Два вектора называются равными,
если
они
коллинеарны,
одинаково
направлены и их длины равны
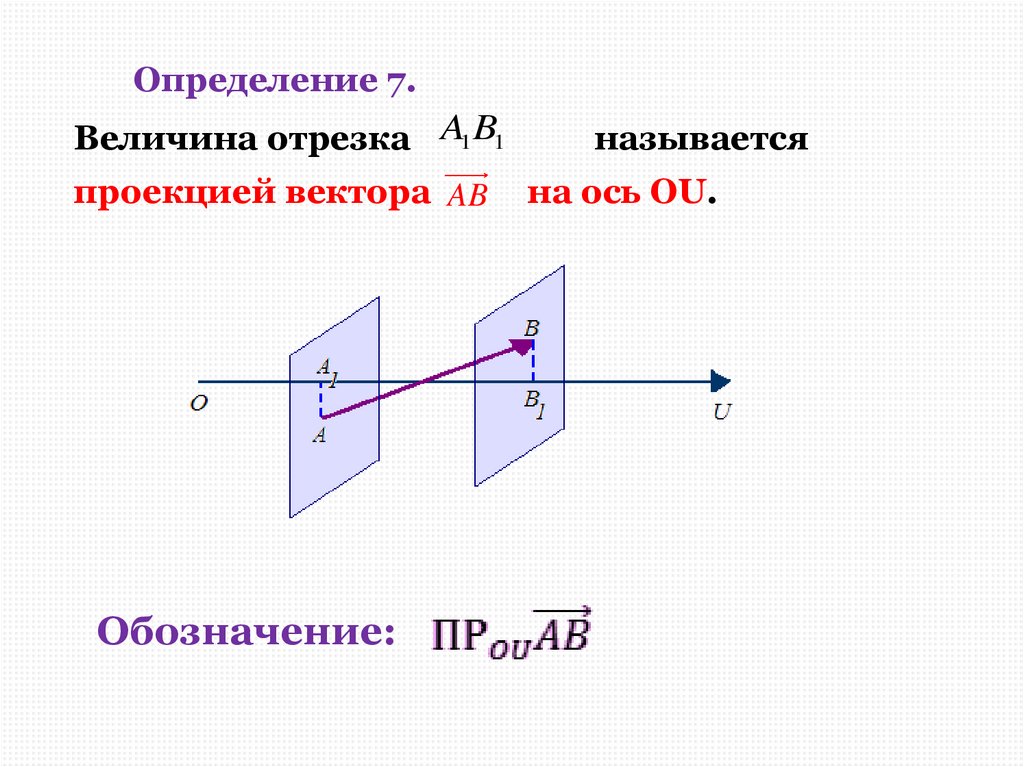
7. 1.2. Проекция вектора на ось
Определение 7.Осью называется прямая, на которой
установлено положительное направление.
Ось OU вполне определяется своим
единичным вектором e .
8.
Рассмотрим вектор AB .Через
точки
А
и
В
проведем
плоскости перпендикулярные оси OU.
Пусть A1 , B1
- точки пересечения
этих плоскостей с осью.
9.
Определение 7.Величина отрезка A1 B1
проекцией вектора AB
Обозначение:
называется
на ось OU.
10.
Определение 8.Проекции вектора AB на
координатные оси OX, OY, OZ
называются координатами вектора.
11. Свойства проекций векторов
1. ПРOUa1 a2 ПРOU a1 ПРOU a2
2. ПРOU a ПРOU a
3. ПРOU AB AB cos ,
AB OU
12. 1.3. Длина вектора
a X ,Y , ZПусть вектор
исходит из начала
координат.
Длину вектора можно
рассматривать как длину
диагонали
параллелепипеда:
2
OA OX 2 OY 2 OZ 2 a X 2 Y 2 Z 2
13.
ЕслиA x1 , y1 , z1 ,
B x2 , y2 , z2 , тогда
• координаты вектора AB
будут
AB x2 x1 , y2 y1 , z2 z1
•длина вектора будет равна
AB
x2 x1 y2 y1 z2 z1
2
2
2
14.
1.4. Линейные операции надвекторами
15.
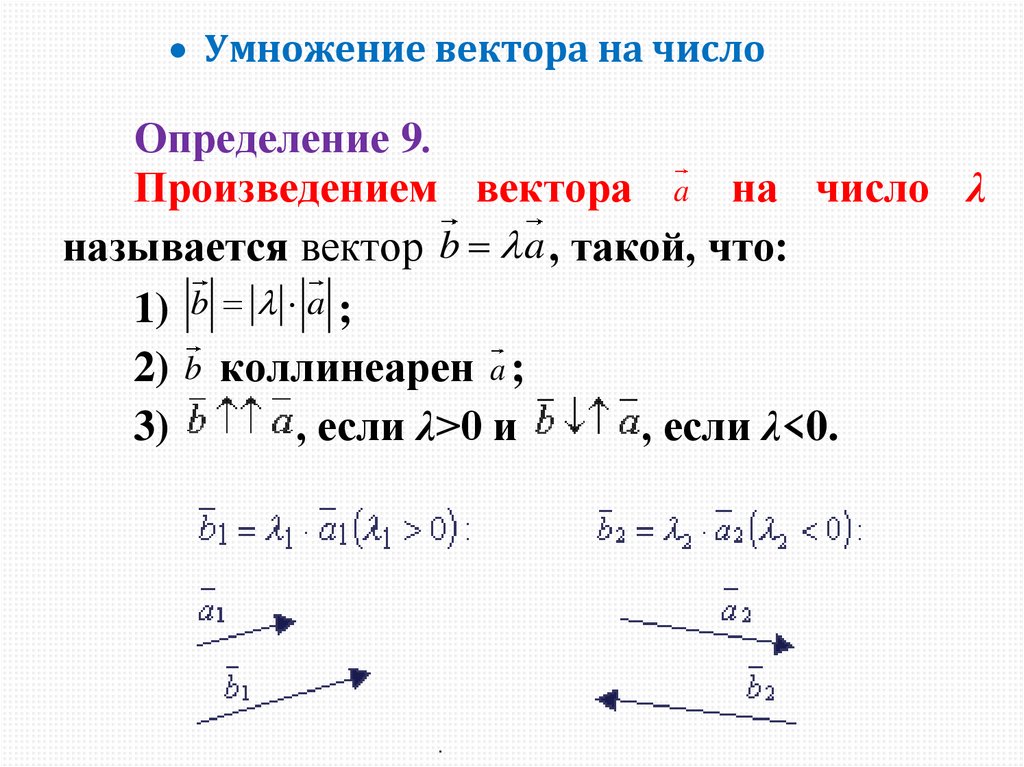
Умножение вектора на числоОпределение 9.
Произведением вектора a на число λ
называется вектор b a , такой, что:
1) b a ;
2) b коллинеарен a ;
, если λ<0.
, если λ>0 и
3)
16.
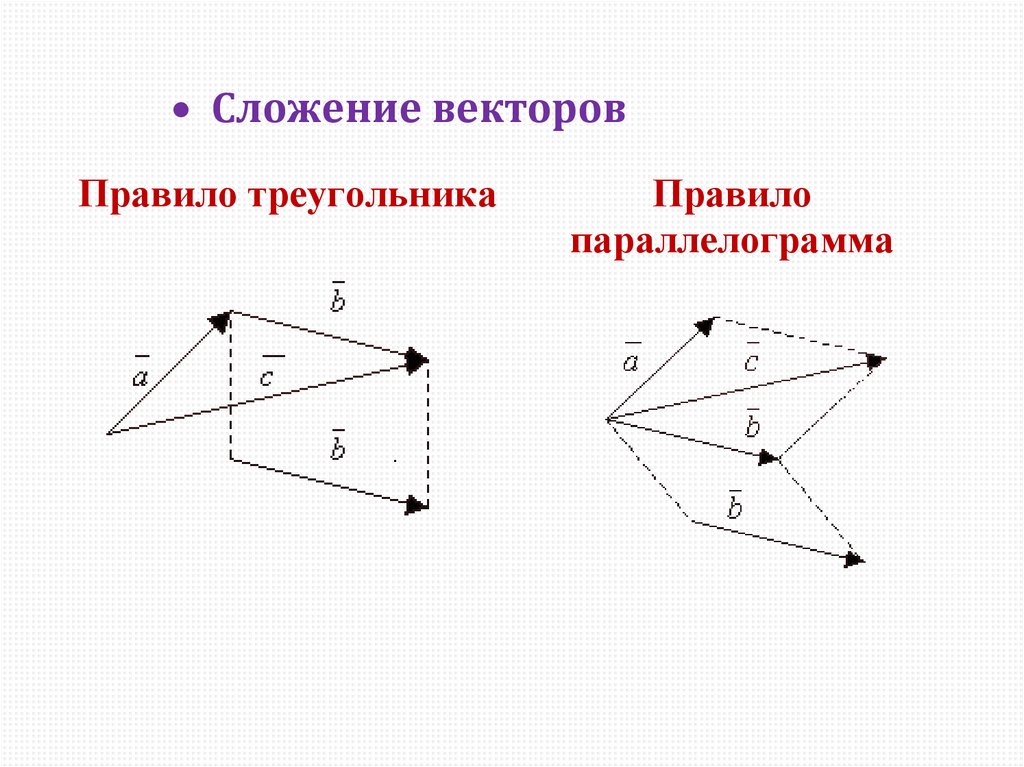
Сложение векторовПравило треугольника
Правило
параллелограмма
17.
• Если a x, y, z , тогда векторa x, y, z
• Если a x1 , y1 , z1 b x2 , y2 , z2
тогда вектор
a b x1 x2 , y1 y2 , z1 z2
18.
Определение 10.Вектор 1 a называется
противоположным к вектору a и
обозначается a .
19.
Определение 11.Разностью векторов b и a называется
вектор c b a .
















 mathematics
mathematics








