МЕТОД_ПРОЕЦИРОВАНИЯ_ПРОЕЦИРОВАНИЕ_ТОЧКИ!!!

1.

*
Тема: МЕТОД ПРОЕЦИРОВАНИЯ.
ПРОЕЦИРОВАНИЕ ТОЧКИ

2.

План изложения темы
1 Метод проецирования
2 Проецирование точки на три плоскости
проекций
3 Комплексный чертеж точки
4 Измерения и координаты точки
5 Положение точек относительно плоскостей
проекций
6 Построение третьей проекции точки по двум
другим

3.

Для построения изображений предметов на плоскости пользуются
МЕТОДОМ ПРОЕЦИРОВАНИЯ
ОПРЕДЕЛЕНИЯ:
ПРОЕКЦИЯ –
изображение предмета,
«отброшенное» на плоскость при помощи лучей
СПРОЕЦИРОВАТЬ ПРЕДМЕТ НА ПЛОСКОСТЬ –
это значит построить его
изображение на плоскости

4.

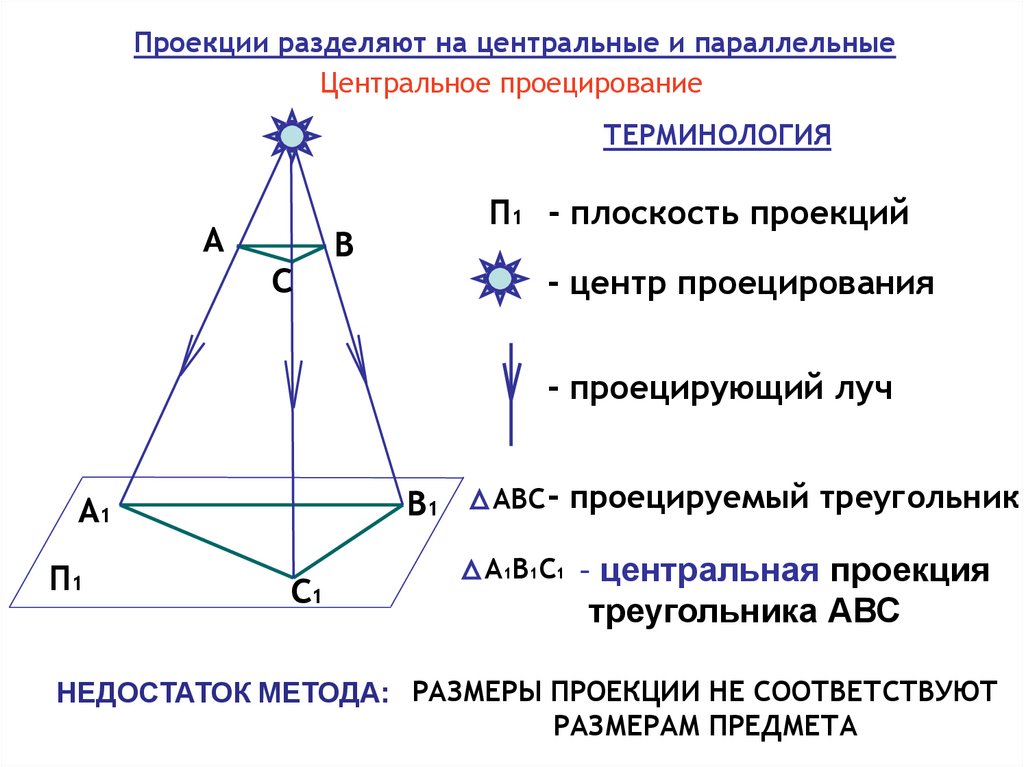
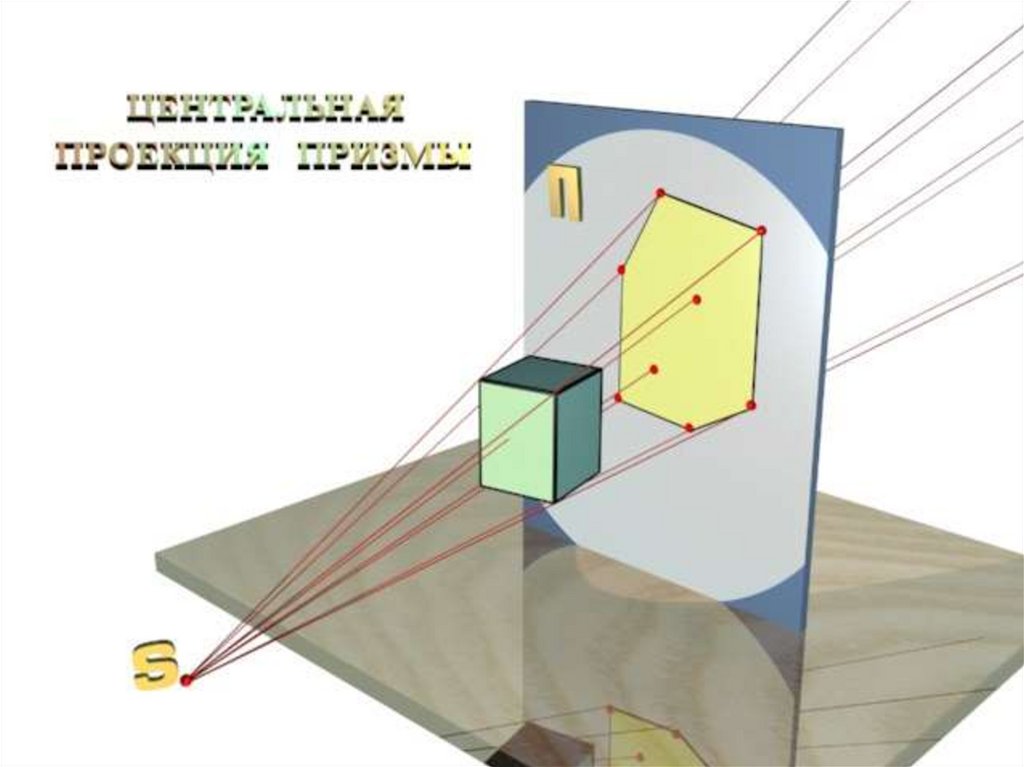
Проекции разделяют на центральные и параллельные
Центральное проецирование
ТЕРМИНОЛОГИЯ
А
С
П1 - плоскость проекций
В
- центр проецирования
- проецирующий луч
В1
А1
П1
С1
АВС - проецируемый треугольник
А1В1С1 - центральная проекция
треугольника АВС
НЕДОСТАТОК МЕТОДА: РАЗМЕРЫ ПРОЕКЦИИ НЕ СООТВЕТСТВУЮТ
РАЗМЕРАМ ПРЕДМЕТА

5.

6. Центральная проекция шара

7.

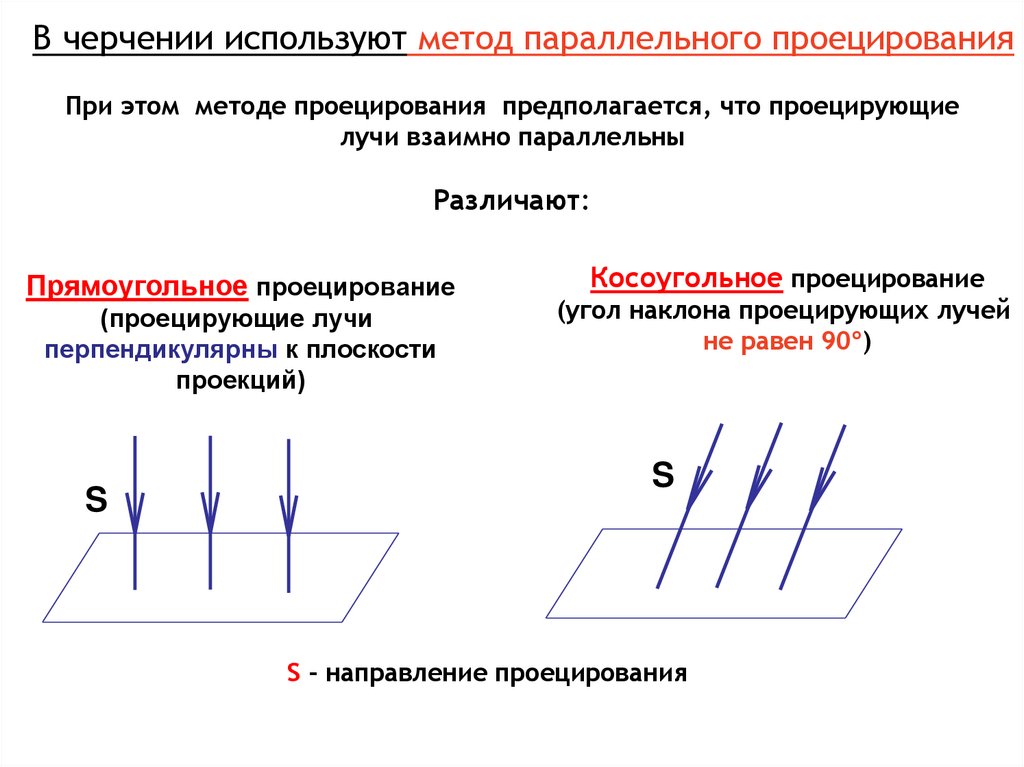
В черчении используют метод параллельного проецирования
При этом методе проецирования предполагается, что проецирующие
лучи взаимно параллельны
Различают:
Прямоугольное проецирование
(проецирующие лучи
перпендикулярны к плоскости
проекций)
S
Косоугольное проецирование
(угол наклона проецирующих лучей
не равен 90º)
S
S - направление проецирования

8.

ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ПЛОСКОСТИ ПРОЕКЦИЙ
Чтобы выполнять прямоугольные проекции
предметов,
надо научиться находить проекции
отдельных точек
Построим проекции точки А на три
взаимно перпендикулярные плоскости

9.

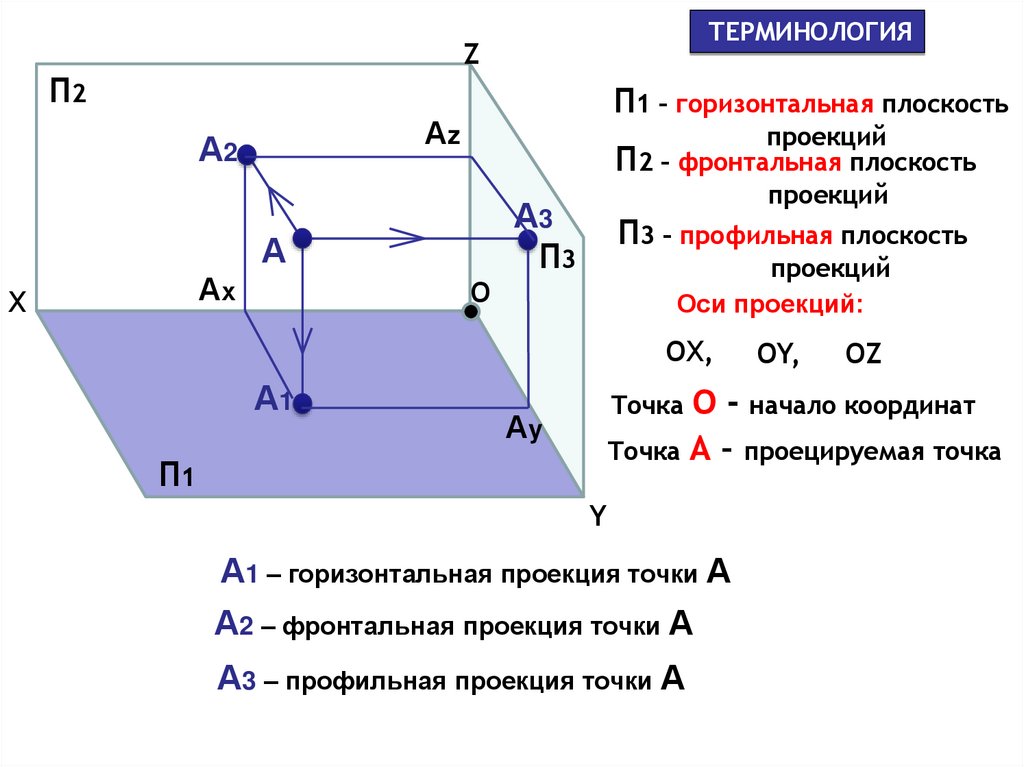
ТЕРМИНОЛОГИЯ
Z
П2
П1 – горизонтальная плоскость
Аz
А2
А3
П3
А
Ах
Х
проекций
П2 – фронтальная плоскость
проекций
П3 – профильная плоскость
проекций
Оси проекций:
О
ОХ,
А1
ОY,
ОZ
Точка О - начало координат
Аy
Точка А – проецируемая точка
П1
Y
А1 – горизонтальная проекция точки А
А2 – фронтальная проекция точки А
А3 – профильная проекция точки А

10.

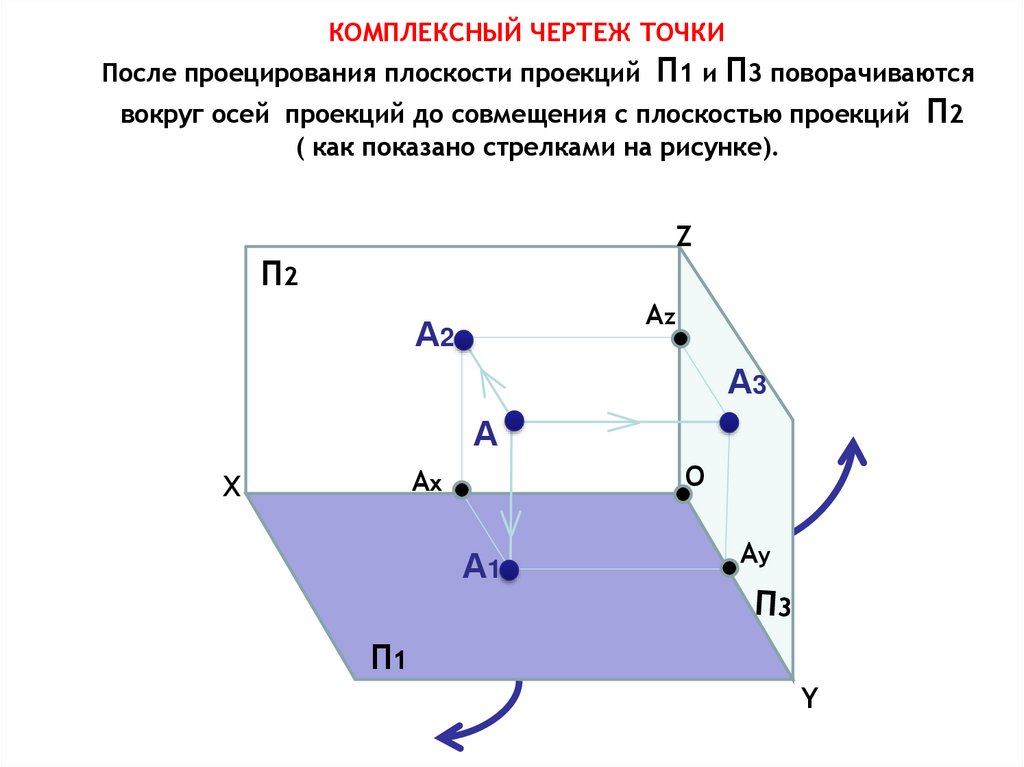
КОМПЛЕКСНЫЙ ЧЕРТЕЖ ТОЧКИ
После проецирования плоскости проекций П1 и П3 поворачиваются
вокруг осей проекций до совмещения с плоскостью проекций П2
( как показано стрелками на рисунке).
Z
П2
Аz
А2
А3
А
О
Ах
Х
А1
Аy
П1
Y

11.

12.

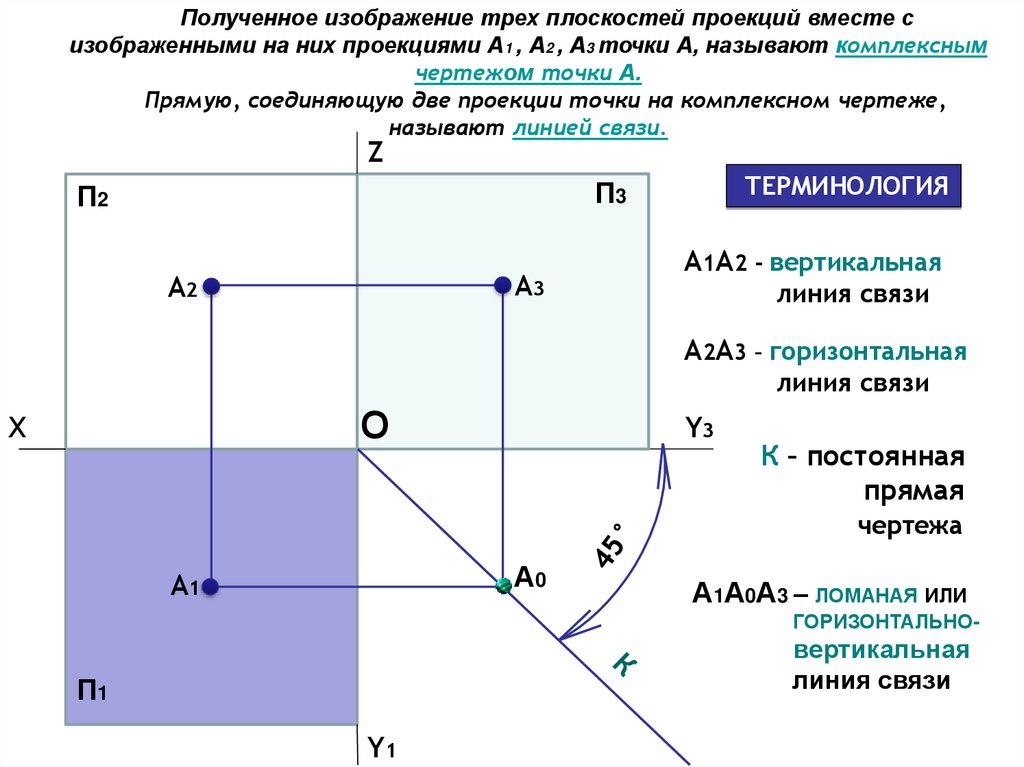
Полученное изображение трех плоскостей проекций вместе с
изображенными на них проекциями А1 , А2 , А3 точки А, называют комплексным
чертежом точки А.
Прямую, соединяющую две проекции точки на комплексном чертеже,
называют линией связи.
Z
ТЕРМИНОЛОГИЯ
П3
П2
А3
А2
А1А2 - вертикальная
линия связи
А2А3 – горизонтальная
линия связи
О
Х
Y3
К – постоянная
прямая
чертежа
А0
А1
А1А0А3 – ЛОМАНАЯ ИЛИ
ГОРИЗОНТАЛЬНО-
вертикальная
линия связи
П1
Y1

13.

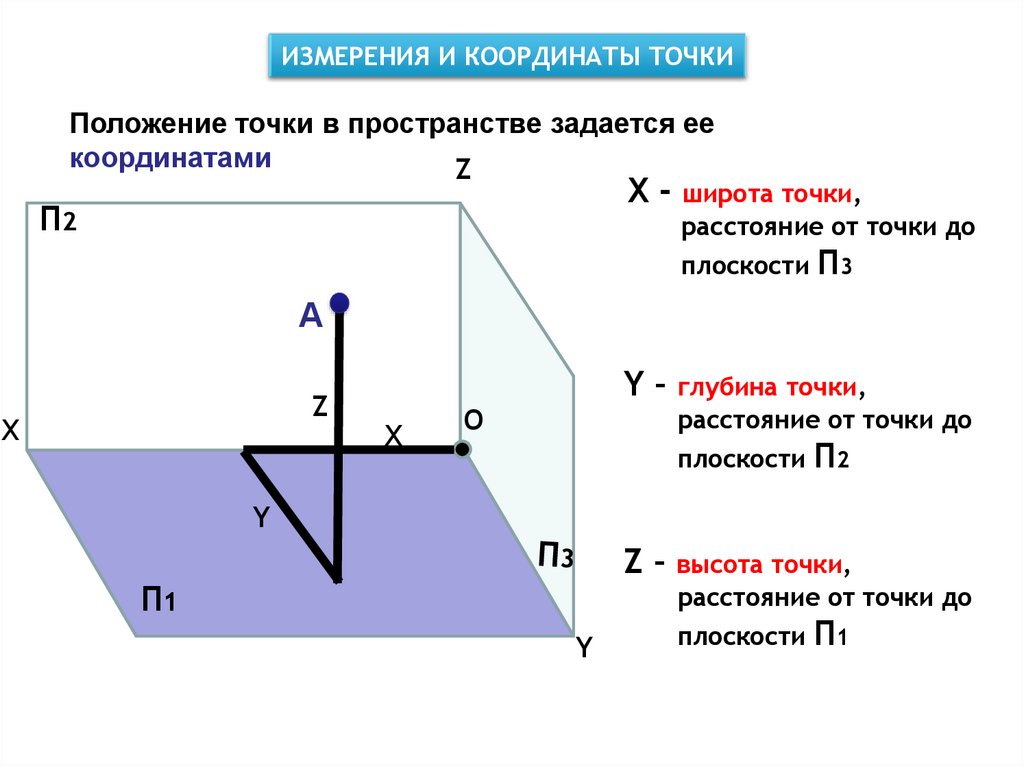
ИЗМЕРЕНИЯ И КООРДИНАТЫ ТОЧКИ
Положение точки в пространстве задается ее
координатами
Z
Х - широта точки,
П2
расстояние от точки до
плоскости П3
А
Z
Х
Y – глубина точки,
Х
О
расстояние от точки до
плоскости П2
Y
Z – высота точки,
П1
расстояние от точки до
Y
плоскости П1

14.

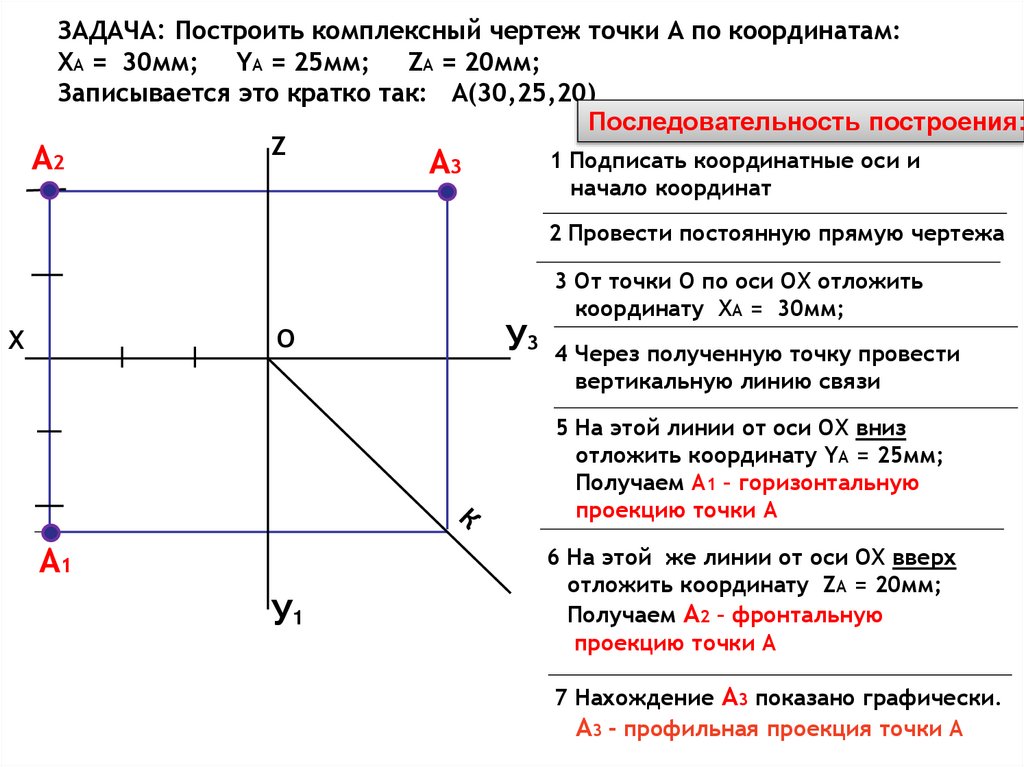
ЗАДАЧА: Построить комплексный чертеж точки А по координатам:
ХА = 30мм; YА = 25мм; ZА = 20мм;
Записывается это кратко так: А(30,25,20)
Последовательность построения:
Z
А2
А3
1 Подписать координатные оси и
начало координат
2 Провести постоянную прямую чертежа
3 От точки О по оси ОХ отложить
координату ХА = 30мм;
О
Х
У3 4 Через полученную точку провести
вертикальную линию связи
5 На этой линии от оси ОХ вниз
отложить координату YА = 25мм;
Получаем А1 – горизонтальную
проекцию точки А
А1
У1
6 На этой же линии от оси ОХ вверх
отложить координату ZА = 20мм;
Получаем А2 – фронтальную
проекцию точки А
7 Нахождение А3 показано графически.
А3 - профильная проекция точки А

15.

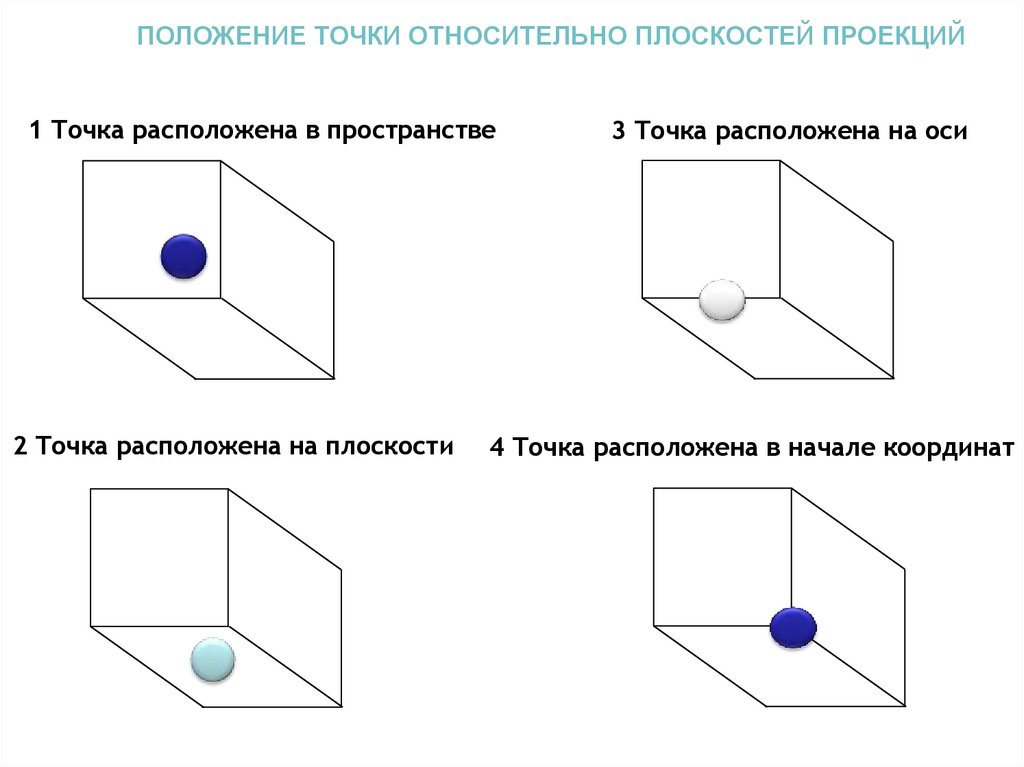
ПОЛОЖЕНИЕ ТОЧКИ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
1 Точка расположена в пространстве
2 Точка расположена на плоскости
3 Точка расположена на оси
4 Точка расположена в начале координат

16.

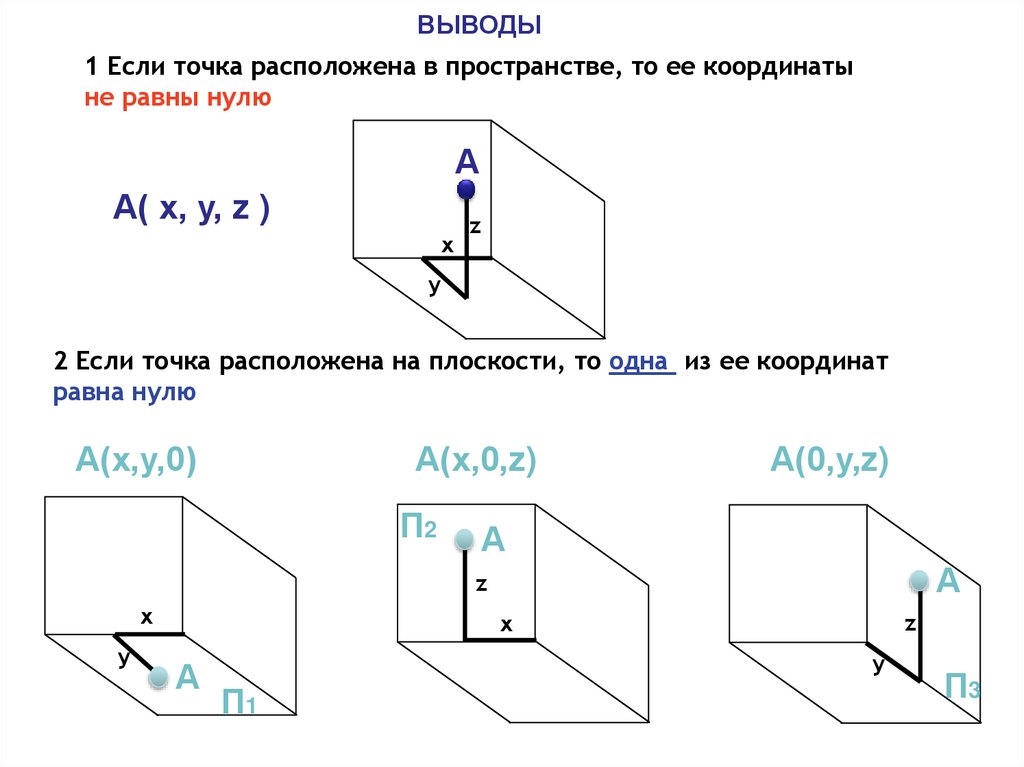
ВЫВОДЫ
1 Если точка расположена в пространстве, то ее координаты
не равны нулю
А
А( х, у, z )
x
z
y
2 Если точка расположена на плоскости, то одна из ее координат
равна нулю
А(х,у,0)
А(х,0,z)
П2
А(0,у,z)
А
А
z
x
y
z
x
А
y
П1
П3

17.

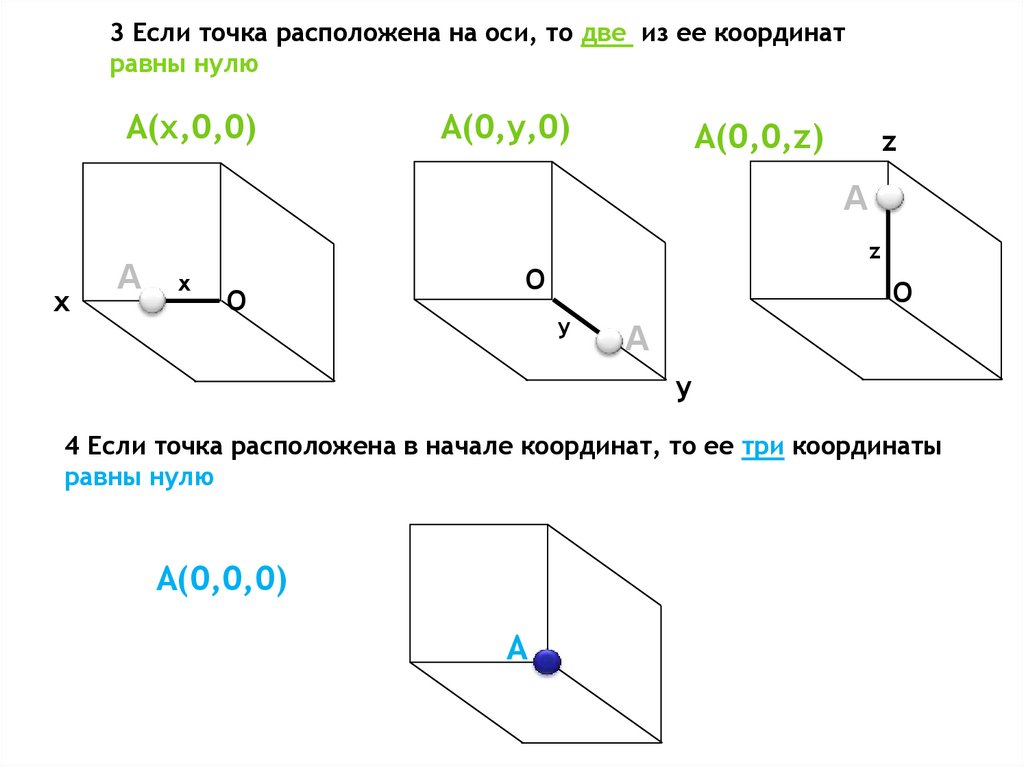
3 Если точка расположена на оси, то две из ее координат
равны нулю
А(х,0,0)
А(0,у,0)
А(0,0,z)
z
А
х
А
x
О
z
О
О
y
А
у
4 Если точка расположена в начале координат, то ее три координаты
равны нулю
А(0,0,0)
А

18.

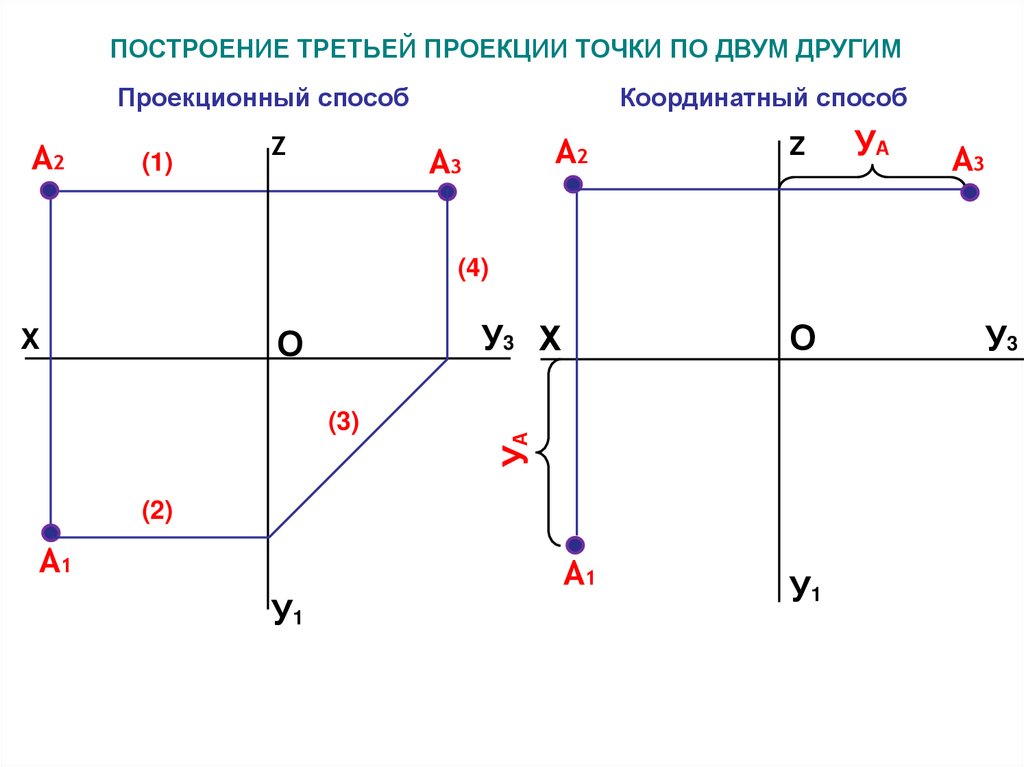
ПОСТРОЕНИЕ ТРЕТЬЕЙ ПРОЕКЦИИ ТОЧКИ ПО ДВУМ ДРУГИМ
Проекционный способ
А2
(1)
Z
Координатный способ
А2
А3
Z
УА
А3
(4)
У3 Х
О
(3)
О
УА
Х
(2)
А1
А1
У1
У1
У3

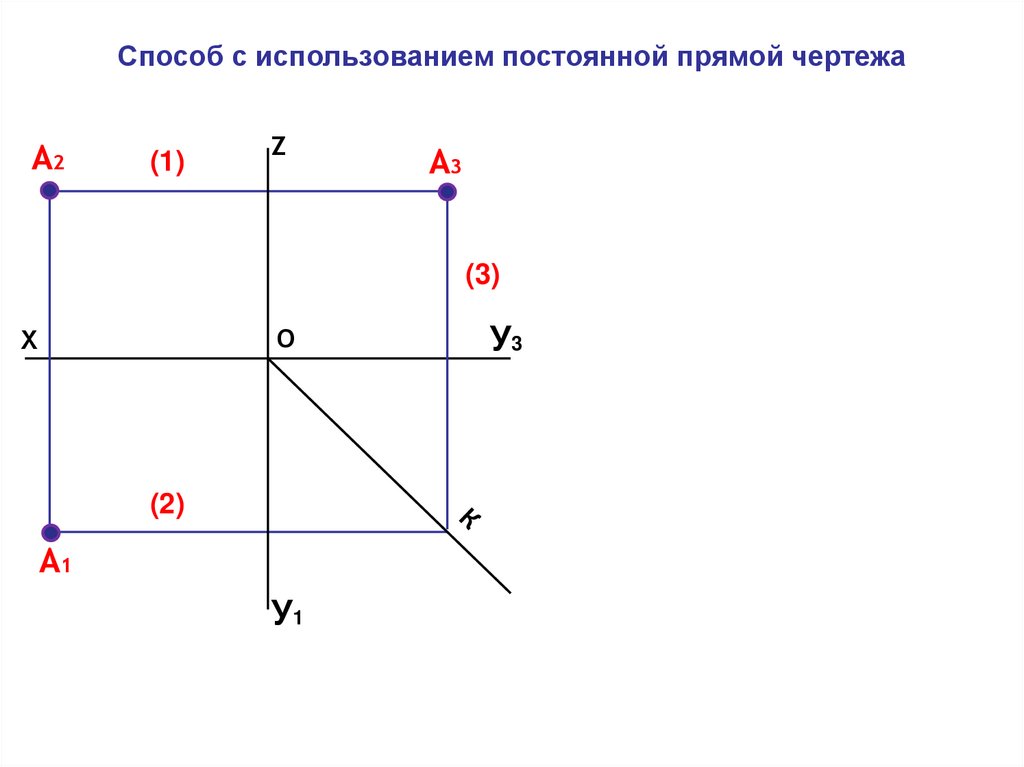
19.

Способ с использованием постоянной прямой чертежа
А2
(1)
Z
А3
(3)
О
Х
(2)
А1
У1
У3

20.

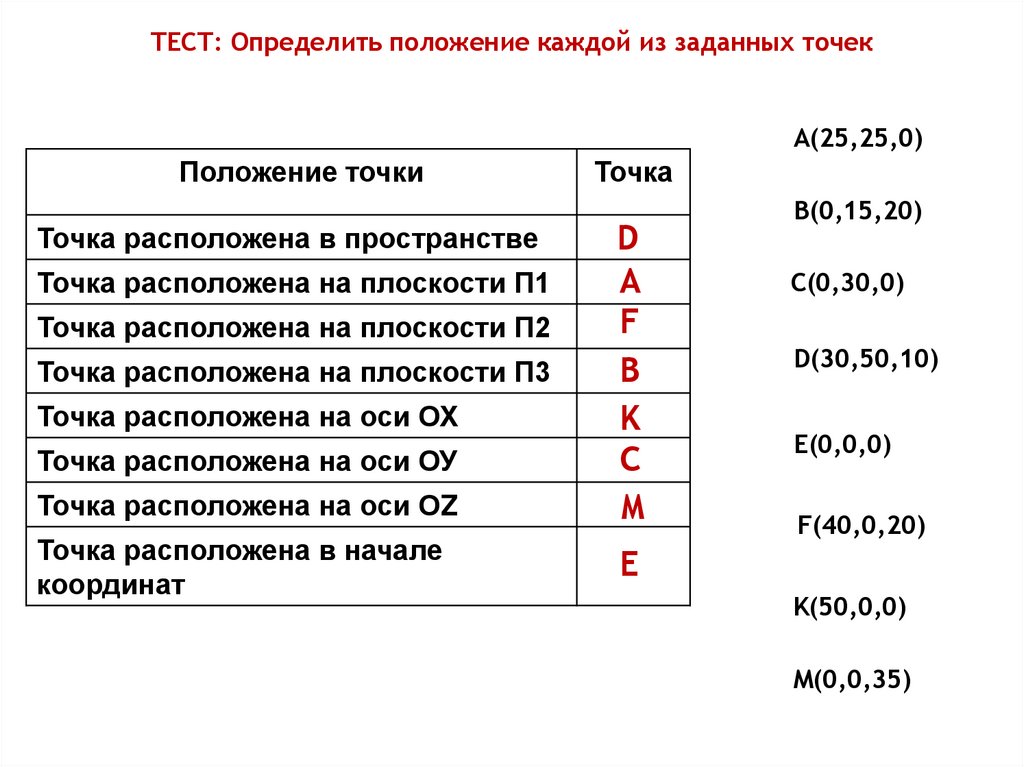
ТЕСТ: Определить положение каждой из заданных точек
А(25,25,0)
Положение точки
Точка расположена в пространстве
Точка расположена на плоскости П1
Точка расположена на плоскости П2
Точка расположена на плоскости П3
Точка расположена на оси ОХ
Точка расположена на оси ОУ
Точка расположена на оси ОZ
Точка расположена в начале
координат
Точка
D
A
F
B
K
C
M
В(0,15,20)
С(0,30,0)
D(30,50,10)
E(0,0,0)
F(40,0,20)
E
K(50,0,0)
M(0,0,35)

21.

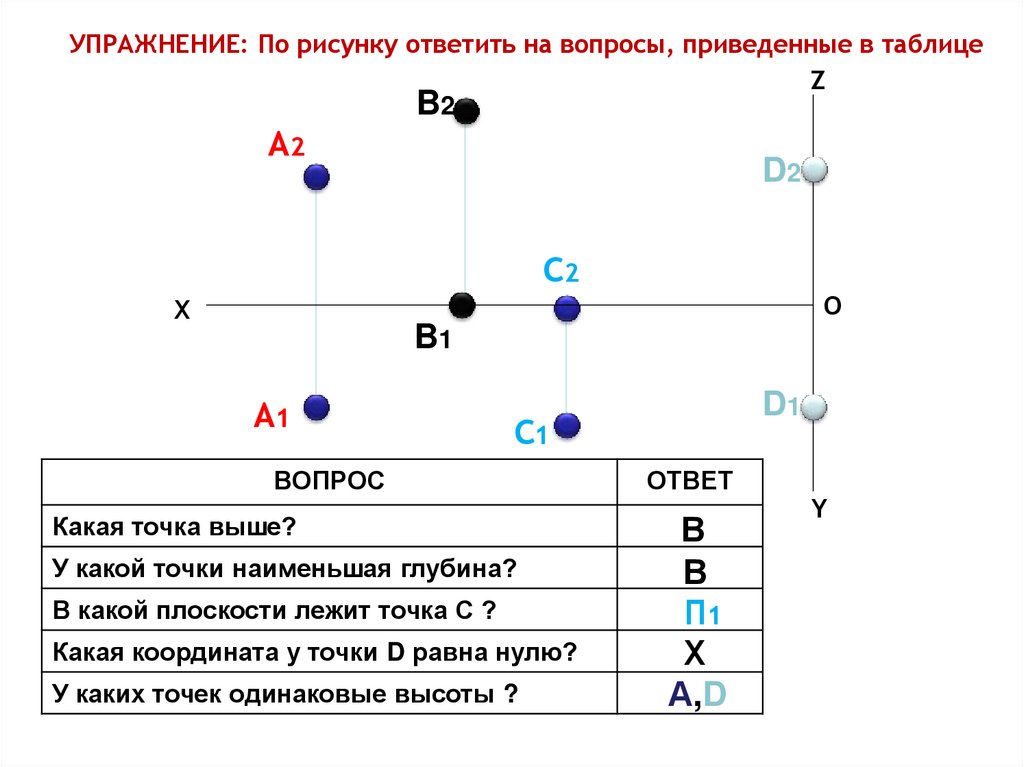
УПРАЖНЕНИЕ: По рисунку ответить на вопросы, приведенные в таблице
Z
B2
A2
D2
C2
О
X
B1
A1
D1
C1
ВОПРОС
Какая точка выше?
У какой точки наименьшая глубина?
В какой плоскости лежит точка С ?
Какая координата у точки D равна нулю?
У каких точек одинаковые высоты ?
ОТВЕТ
В
В
П1
Х
А,D
Y

22.

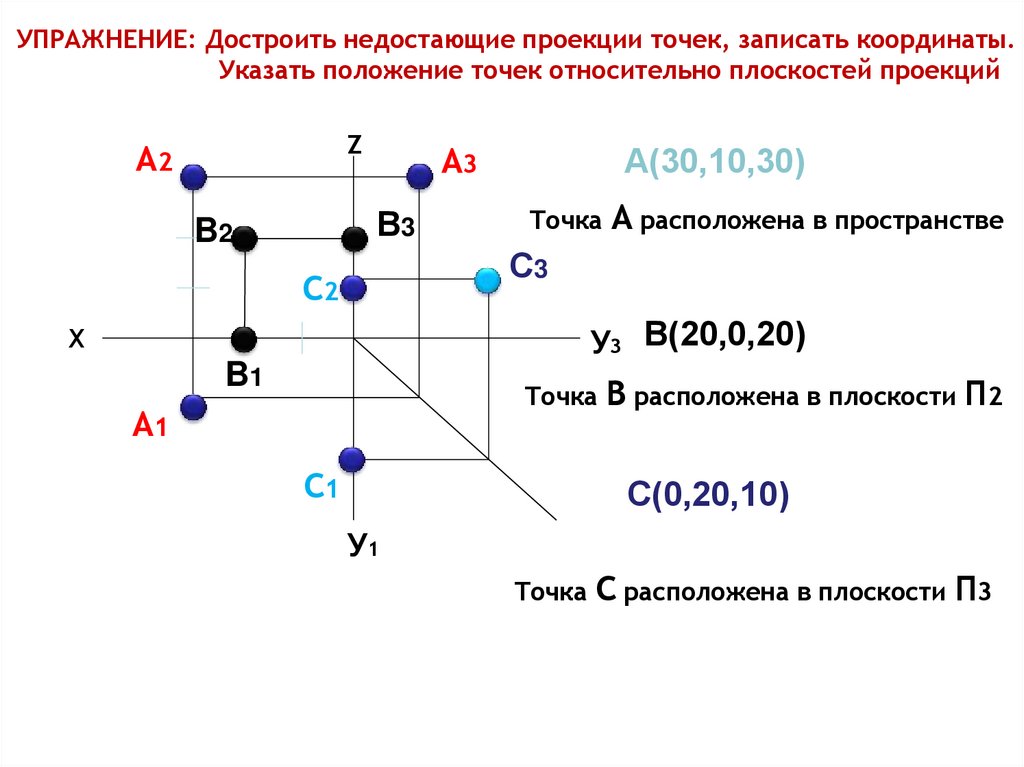
УПРАЖНЕНИЕ: Достроить недостающие проекции точек, записать координаты.
Указать положение точек относительно плоскостей проекций
Z
A2
A3
В3
B2
А(30,10,30)
Точка А расположена в пространстве
С3
C2
У3 В(20,0,20)
Х
B1
Точка В расположена в плоскости П2
A1
C1
С(0,20,10)
У1
Точка С расположена в плоскости П3

23.

ИЗ ИСТОРИИ ТОЧКИ
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
* А.П.Целковская
Мы с детства знакомы, конечно, незримо
С историей Греции, Древнего Рима…
Десятки столетий, ни Цезарь, ни Данте
Не знали о точке, живущей в октанте.
И даже октанты ещё там не знали –
Пространство вокруг все единым считали!
Но вот восемнадцатый век на исходе…
Царят неспокойно все бунты в народе.
А в тесной казарме вблизи от Парижа
Скучает Геометр… к науке он ближе,
Чем к ратным походам, к казарменным нарам
И звали его по-французски Гаспаром.
Он точку представил как плоскость проекций,
И стала та плоскость объектом для лекций.
Почти что два века, без мук перемены,
История точки не сходит со сцены!
Студент-второкурсник, как часто бывает,
Проекцию точки с трудом понимает.
И трудности эти слегка одолели
Созданием плоских, объектных моделей.
Теперь, как звезда, на фасаде и в плане
Проекция точки горит на экране