Л2 умножение вектров

1. Векторная алгебра

Умножение векторов

2.

3.

4.

5.

6.

7.

8.

9.

10.

11. Векторное произведение

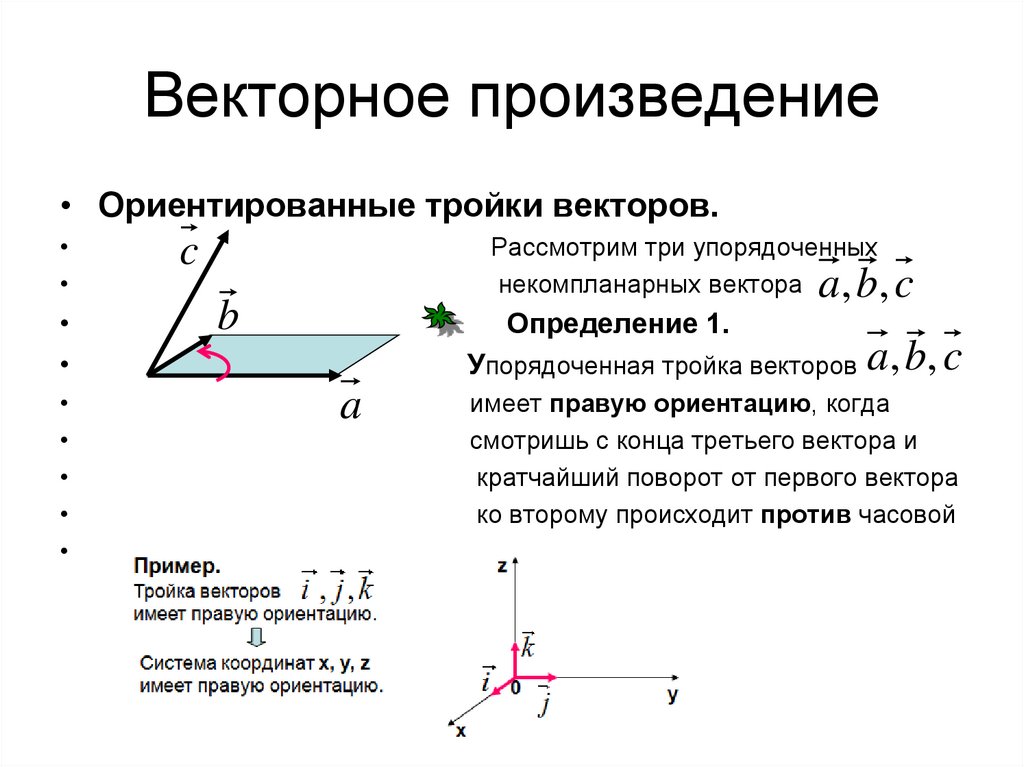
• Ориентированные тройки векторов.
Рассмотрим три упорядоченных
некомпланарных вектора
c
a , b, c
b
Определение 1.
Упорядоченная тройка векторов a , b, c
a
имеет правую ориентацию, когда
смотришь с конца третьего вектора и
кратчайший поворот от первого вектора
ко второму происходит против часовой
стрелки.

12. Векторное произведение

• Свойства векторного произведения.
• 1. a b b a
• 2. ( a ) b (a b)
• 3. a (b c) a b a c
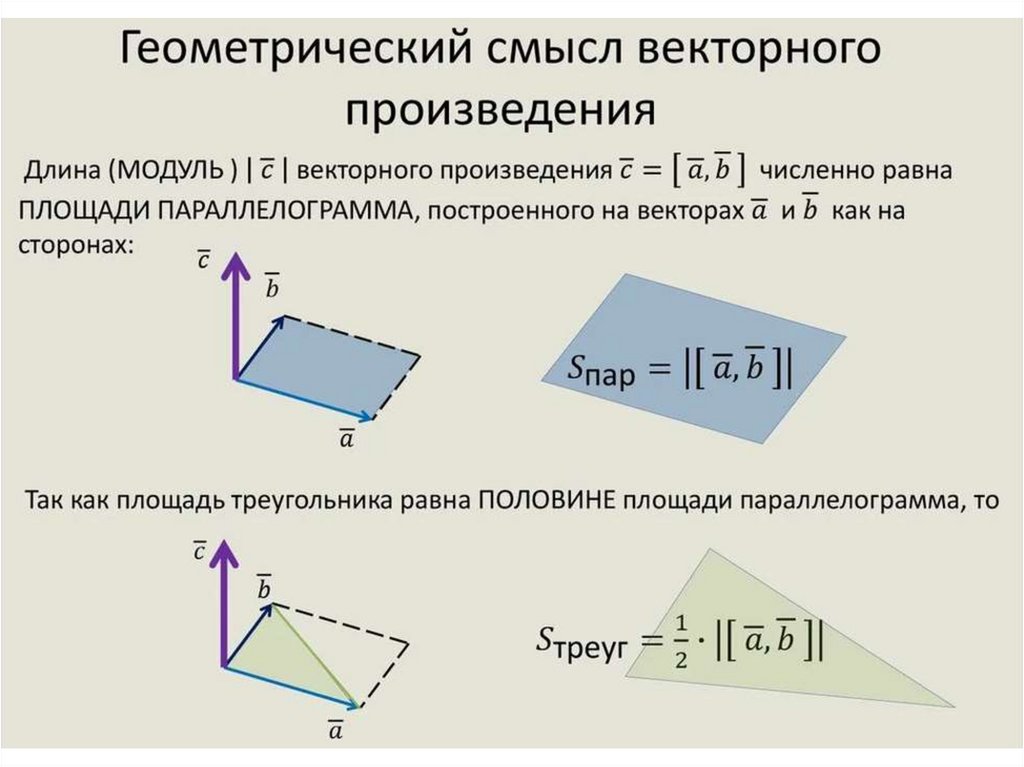
• 4. Геометрический смысл .
Модуль векторного произведения двух векторов
численно равен площади параллелограмма,
построенного на этих векторах:
a b S
b
a

13.

14. Векторное произведение

• 5. Необходимое и достаточное условие
коллинеарности двух векторов.
Два ненулевых вектора коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулевому вектору:
a b a b 0
• 6. a a 0
a
b

15.

16.

17.

18. Векторное произведение

• Физический смысл.
M (F )
A
А
В
F
Пусть к твердому телу,
закрепленному в точке А,
приложена в точке В сила F
Момент силы F , приложенной
в точке В, относительно точки А
равен векторному произведению
вектора
AB и силы F :
M A ( F ) AB F

19.

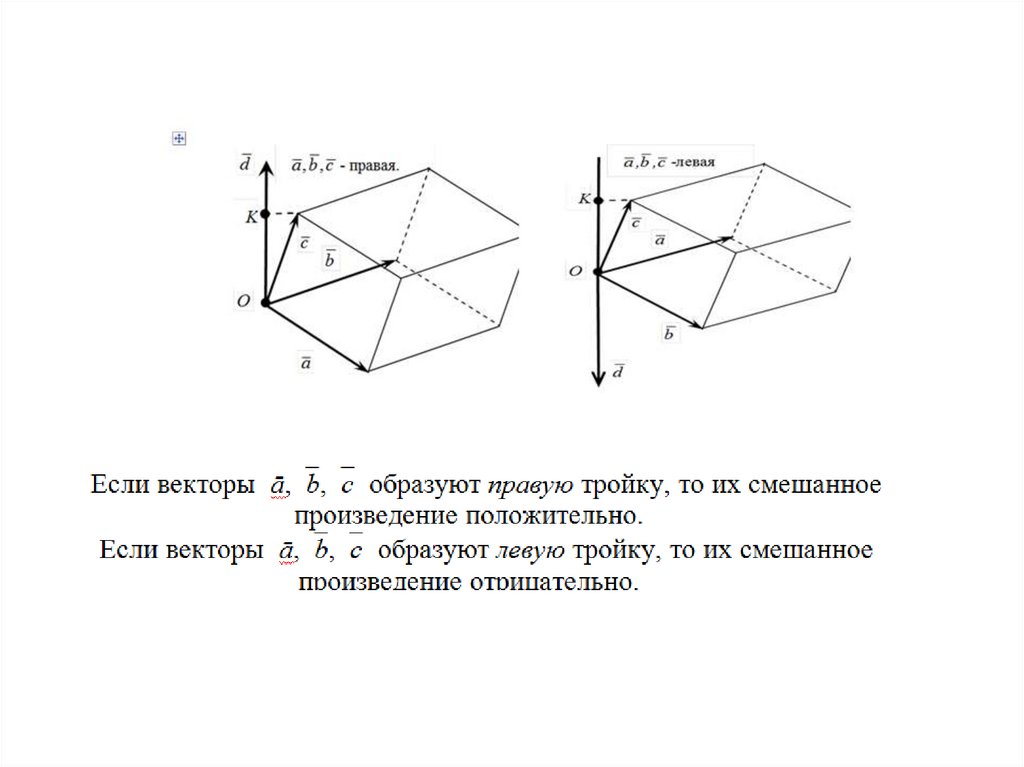
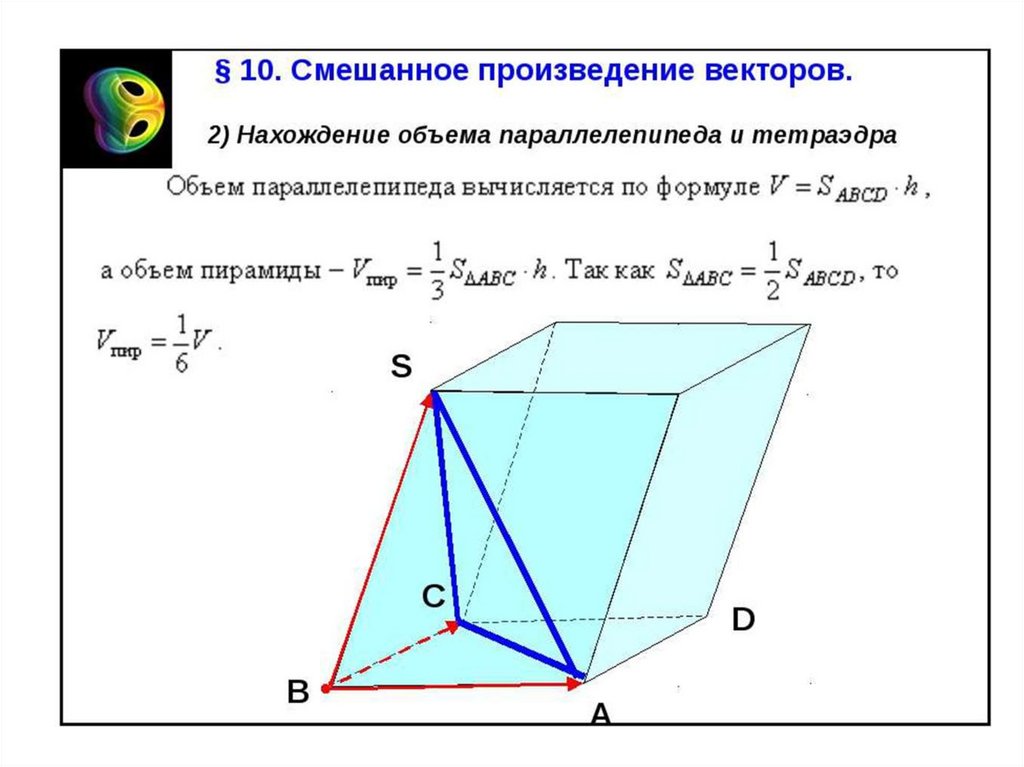
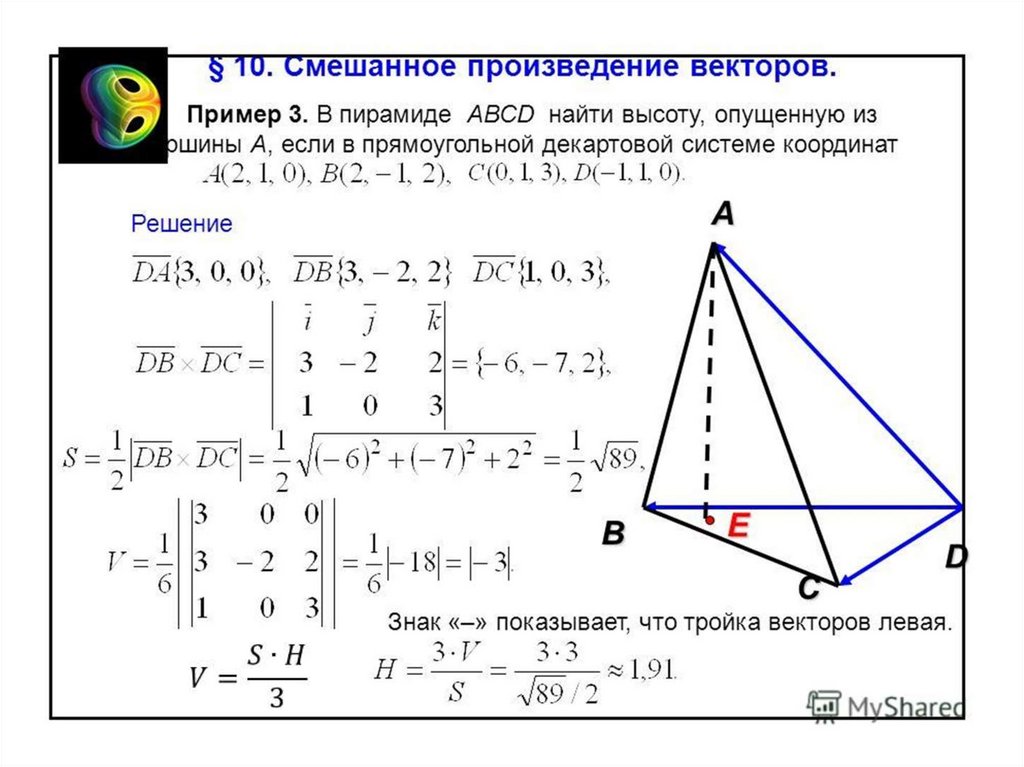
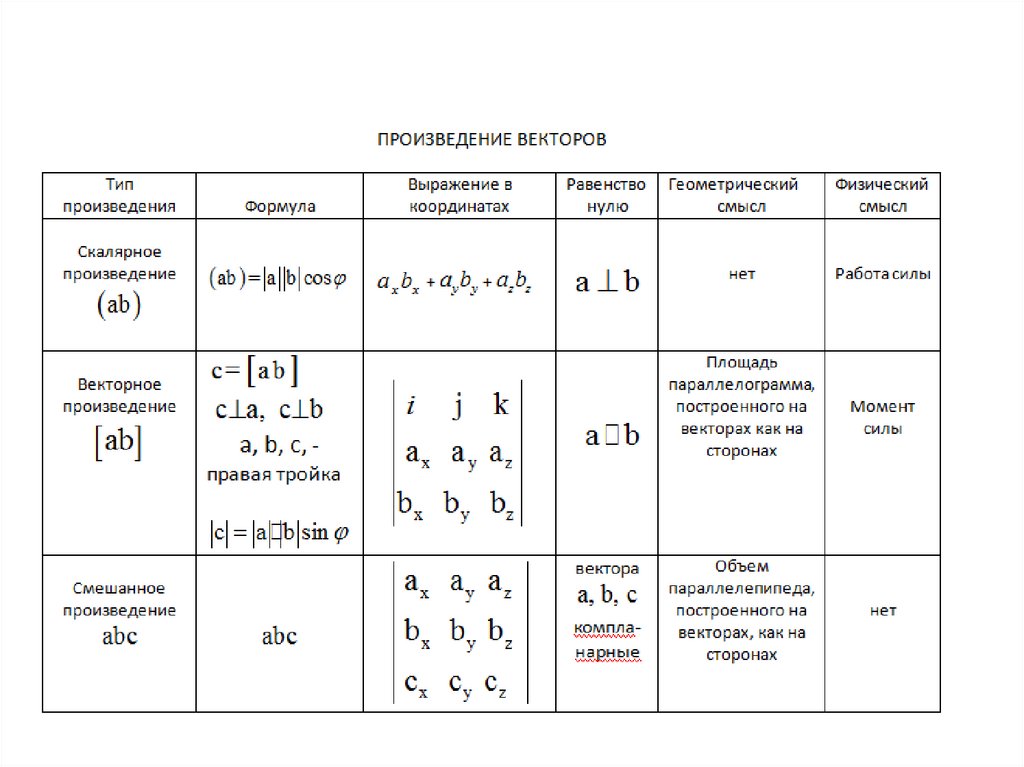
20. Смешанное произведение

• Определение.
Смешанным произведением трех векторов
называется векторное произведение первых двух
векторов, умноженное скалярно на третий вектор:
Обозначения:
Замечание.
Результат смешанного произведения трех векторов
является скалярной величиной.
a b c ( a , b, c )