СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ

1.

СТРОИТЕЛЬНАЯ МЕХАНИКА
СТАТИЧЕСКИ
НЕОПРЕДЕЛИМЫЕ
СИСТЕМЫ
Расчёт СНС методом сил

2.

РАСЧЁТ СНС МЕТОДОМ СИЛ
в матричной форме
Канонические уравнения метода сил (КУМС):
δ X ΔΣ 0
Коэффициенты КУМС (единичные перемещения в ОСМС):
δ ik Lтi B Lk δ Lт B L
Li , Lk – векторы усилий в расчётных сечениях
расчётных участков ОСМС в i-м и k-м
L = [ L1…Li …Ln ] –
единичных состояниях (от Xi = 1 и Xk = 1);
B – матрица внутренней упругой податливости ОСМС;
матрица усилий
в единичных
состояниях ОСМС.
Свободные члены КУМС
(перемещения в ОСМС от заданных воздействий):
ΔiΣ Lт0,i B0 LΣ
Δ iF Lтi B LF
Δit Lтt,i Bt T
Δ Σ Lт0 B0 LΣ
Δic RΔт ,i ( E ) Δ( c )
LF
L
L0 Lt ; LΣ T .
Δ( c )
B = diag [ B Bt –E ];
RΔ

3.

РАСЧЁТ СНС МЕТОДОМ СИЛ
в матричной форме
Основные неизвестные:
X ( Lт B L) 1 Lт0 B0 L
Искомые усилия:
S L X L*
( в случае СО ОСМС L LF )
*
а) в характерных сечениях
расчётных участков:
S L* L ( Lт B L) 1 Lт0 B0 L
– 5 исходных матриц
б) в назначенных сечениях:
~ ~* ~ т
S L L ( L B L) 1 Lт0 B0 L
– 7 исходных матриц

4.

РАСЧЁТ СНС МЕТОДОМ СИЛ
в матричной форме
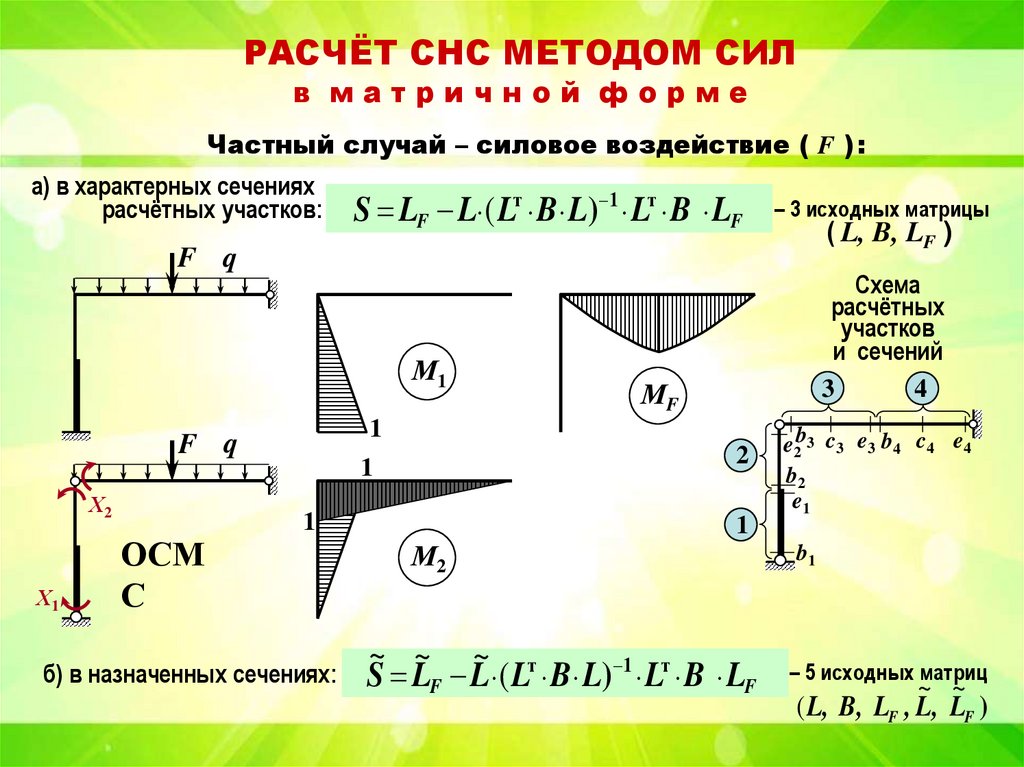
Частный случай – силовое воздействие ( F ) :
а) в характерных сечениях
расчётных участков:
S LF L ( Lт B L) 1 Lт B LF
– 3 исходных матрицы
( L, B, LF )
F q
М1
Х1
ОСМ
С
МF
1
F q
Х2
Cхема
расчётных
участков
и сечений
3
4
2
1
1
б) в назначенных сечениях:
1
М2
~ ~ ~ т
S LF L ( L B L) 1 Lт B LF
e2b3 c3 e3 b4 c4 e4
b2
e1
b1
– 5 исходных матриц
~ ~
( L, B, LF , L, LF )

5.

РАСЧЁТ СНС МЕТОДОМ СИЛ
П л а н - а л г о р и т м расчёта СНС методом сил
Этап (шаг)
С о д е р ж а н и е
1. Кинемат. анализ;
выявление степени
статической
неопределимости
W < 0 (?) ГНС ? (структурный анализ)
степень статической неопределимости nst = nл.с.= – W ( = 3*K – H )
2. Выбор
основной системы
метода сил (ОСМС)
Сравнительный анализ возможных вариантов ОСМС,
выбор рациональной ОСМС, номинация основных неизвестных X
Условия кинематической эквивалентности РСНС и ОСМС: i = 0, i = 1, ..., n
3. Запись
канонических
уравнений
метода сил
(КУМС)
n
Обычная форма
Матричная форма
iΣ
δ X ΔΣ 0
δ X Δ 0, i 1, n
k 1
ik
k
4. Единичные
состояния ОСМС
Определение внутренних силовых факторов Sk M k , Qk , N k
oт Xk = 1, k = 1, …, n
5. Вычисление
коэффициентов
КУМС
Вычисление единичных перемещений ik
m
u R R
Si Sk
j,i
j,k
т
δ ik
ds j
; i, k 1, n
δ
L
BL
C
C
S
j
по S j 1 l j
j 1
6. Действительное
состояние ОСМС
7. Вычисление
свободных
членов КУМС
Определение внутренних силовых факторов S M , Q , N
от заданных воздействий; температурных деформаций rt и e0t
Вычисление перемещений i от силовых, температурн. и кинематич. воздействий
u R R
Si SΣ
j,i
j,Σ
ds j
Cj
по S j 1 l j C S
j 1
m
Δ iΣ Δ iF Δ it Δ ic
m
r
по S j 1 l j
j 1
S i ε S,t ds j R( j ) ,i Δ( j ) ; i 1, n
Δ Σ Lт0 B0 LΣ
Δ F Lт B LF ; Δ t Lтt Bt T ;
т
Δ
R
(
E
)
Δ
c
Δ
(c )

6.

РАСЧЁТ СНС МЕТОДОМ СИЛ
П л а н - а л г о р и т м расчёта СНС методом сил
Этап (шаг)
С о д е р ж а н и е
Суммарное единичное состояние ОСМС – от одновременно приложенных
X1 = 1, X2 = 1, … , Xn = 1; определение суммарных единичных ВСФ S s M s , Qs , N s
Проверка коэффициентов канонических уравнений МС:
а) универсальная проверка коэффициентов :
8. Проверки
обычная форма
m
u R2
n n
S s2
j,s
δ ss ds j
(?) δ ik
по S j 1 l j C s
j 1 C j
i 1 k 1
членов КУМС
n
n
δ ss L B Ls (?) δ ik
т
s
i 1 k 1
б) построчная проверка коэффициентов
коэффициентов
и свободных
матричная форма
(при отрицательном результате универсальной проверки):
u R R
n
Si S s
j,i j,s
δ is
ds j
(?) δ ik ( i 1, n)
Cj
по S j 1 l j C s
j 1
k 1
m
n
δ is L B Ls (?) δ ik
т
i
k 1
Проверка свободных членов канонических уравнений МС:
u R R
S s S
j,s
j,
ds j
C
C
s
j
по S j 1 l j
j 1
m
s
m
r
n
S s e s,t ds j R( j ) ,s ( j ) (?) i
по S j 1 l j
9. Определение
основных
неизвестных Х
(решение КУМС)
j 1
n
s L B0 L (?) i
т
0 ,s
i 1
i 1
Det (δ k )
, k 1, n ;
Det ( )
δ11 δ1 , k 1 ( Δ1Σ ) δ1 , k 1 δ1n
Det (δ k ) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
δ n1 δ n, k 1 ( Δ nΣ ) δ n, k 1 δ nn
Xk
X

7.

РАСЧЁТ СНС МЕТОДОМ СИЛ
П л а н - а л г о р и т м расчёта СНС методом сил
Этап (шаг)
С о д е р ж а н и е
n
10. Вычисление
искомых
усилий
S S k X k S ( S M , Q , N )
k 1
n
M M k X k M Q dM/ds N
k 1
Статическая проверка
(проверка равновесия)
a) S L X L*
L* L ( Lт B L) 1 Lт0 B0 L
~ ~
~
б) S L X L*
~ ~
L* L ( Lт B L) 1 Lт0 B0 L
а) системы в целом
б) узлов
в) выделенных частей
Кинематическая (деформационная) проверка
а) о б щ а я
11. Проверки
результатов
расчёта
R j,s R j
Ss S
ds j
Cj
по S j 1 l j C s
j 1
n
m
u
s i
i 1
m
r
S s e s,t ds j R( j ) ,s ( j ) 0 (?)
по S j 1 l j
j 1
S
s Lт0 ,s B0 T 0 (?)
Δ ( c )
S
т
L0 B0 T 0 (?)
Δ( c )
б) ч а с т н ы е
u R R
Si S
j,i
j
i
ds j
S
Cj
по S j 1 l j C s
j 1
т
( i 1, n) i L0 , i B0 T 0 (?)
m
r
Δ ( c )
S i e s,t ds j R( j ) ,i ( j ) 0 (?)
по S j 1 l
j 1
m
j
u R R
Si S
j,i j
ds j
(Δ it Δ ic ) (?) el Lт B S ( Δ t Δ c ) (?)
по S j 1 l j C s
j 1 C j
m
Вариант:
el
i

8.

РАСЧЁТ СНС МЕТОДОМ СИЛ
Пример
3
6
F = 20 кН
2EI
EI
q = 20 кН/м
Требуется выполнить расчёт статически неопределимой рамы
2EI
1. Кинематический анализ и выявление степени
статической неопределимости заданной системы
М = 40 кН*м
W = 3D – (3H + 2H + C + C0 ) = 3*2 – (3*0 + 2*1 + 0 + 6 ) = – 2 < 0.
EI
6м
EI
a) nst = – W = 2; b) nst = 3K– H = 3*2 – 4 = 2.
2. Выбор основной системы метода сил
6м
ОСМС = РСНС – ЛС + Х
РСНС – рассчитываемая статически неопределимая система;
Рекомендации по выбору
ЛС – лишние связи;
Х – основные неизвестные.
рациональной ОСМС:
1. ОСМС должна по возможности минимально
Варианты ОСМС
отличаться от РСНС по характеру своей работы.
2. Нежелательно удаление линейных связей,
особенно внешних.
3. Удалять угловые связи
(вставлять цилиндрические шарниры)
целесообразно в узлах.
Х2
Х1
4. Предпочтение следует отдавать ОСМС
с простой структурой (если возможно –
то с главными и второстепенными частями).
5. Если РСНС симметрична, то имеет смысл
выбирать симметричную ОСМС.
Х2
Х1
Х2
Х2
Х1
Х1

9.

РАСЧЁТ СНС МЕТОДОМ СИЛ
Пример
3
6
F = 20 кН
2EI
EI
q = 20 кН/м
Требуется выполнить расчёт статически неопределимой рамы
2EI
1. Кинематический анализ и выявление степени
статической неопределимости заданной системы
М = 40 кН*м
W = 3D – (3H + 2H + C + C0 ) = 3*2 – (3*0 + 2*1 + 0 + 6 ) = – 2 < 0.
EI
6м
EI
a) nst = – W = 2; b) nst = 3K– H = 3*2 – 4 = 2.
6м
2. Выбор основной системы метода сил
ОСМС = РСНС – ЛС + Х
РСНС – рассчитываемая статически неопределимая система;
Рекомендации по выбору
ЛС – лишние связи;
Х – основные неизвестные.
рациональной ОСМС:
1. ОСМС должна по возможности минимально
Варианты ОСМС
отличаться от РСНС по характеру своей работы.
2. Нежелательно удаление линейных связей,
особенно внешних.
3. Удалять угловые связи
(вставлять цилиндрические шарниры)
целесообразно в узлах.
4. Предпочтение следует отдавать ОСМС
с простой структурой (если возможно –
то с главными и второстепенными частями).
5. Если РСНС симметрична, то имеет смысл
выбирать симметричную ОСМС.
Х2
Х1
?
Х2
Х1
Х2
Х1

10.

РАСЧЁТ СНС МЕТОДОМ СИЛ
Пример
3
6
F = 20 кН
2EI
EI
q = 20 кН/м
Требуется выполнить расчёт статически неопределимой рамы
2EI
1. Кинематический анализ и выявление степени
статической неопределимости заданной системы
М = 40 кН*м
W = 3D – (3H + 2H + C + C0 ) = 3*2 – (3*0 + 2*1 + 0 + 6 ) = – 2 < 0.
EI
6м
EI
a) nst = – W = 2; b) nst = 3K– H = 3*2 – 4 = 2.
6м
2. Выбор основной системы метода сил
ОСМС = РСНС – ЛС + Х
РСНС – рассчитываемая статически неопределимая система;
Рекомендации по выбору
ЛС – лишние связи;
Х – основные неизвестные.
рациональной ОСМС:
1. ОСМС доджна по возможности минимально
Варианты ОСМС
отличаться от РСНС по характеру своей работы.
2. Нежелательно удаление линейных связей,
особенно внешних.
3. Удалять угловые связи
(вставлять цилиндрические шарниры)
целесообразно в узлах.
4. Предпочтение следует отдавать ОСМС
с простой структурой (если возможно –
то с главными и второстепенными частями).
5. Если РСНС симметрична, то имеет смысл
выбирать симметричную ОСМС.
Х2
Х2
Х1
?
Х1

11.

Контрольные вопросы
*) Только в режиме «Показ слайдов».
См. также тему «Матричная форма определения
перемещений линейно деформируемых систем»
( в скобках даны номера слайдов, в которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 21» )
1. Матричные выражения для вычисления:
а) величин ik , i , iF , it , ic ( 2 ) ;
б) матриц , , F , t , c ( 2 ) ;
в) основных неизвестных Х ( 3 ) .
2. Как называется каждая из матриц L, B и LF ? ( 2 )
3. Какую структуру (поблочно) и размеры (число строк и столбцов) имеют матрицы
L, B и LF ? Как взаимно согласуются размеры и структура этих матриц?
4. Какой смысл имеют компоненты i-го столбца матрицы L ? ( 2 ) f-го столбца
матрицы LF ?
5. Назначение расчётных участков и расчётных сечений элементов с упругими
и температурными деформациями при выполнении расчёта СНС методом сил
в матричной форме (правила, возможности рационального сокращения числа
расчётных сечений) ( 4 ) .
6. Вид матриц внутренней упругой податливости расчётных участков с различным
числом (3, 2, 1) расчётных сечений.
7. Какие силовые факторы описываются матрицами L и LF при расчёте:
а) балок; б) рам; в) арок; г) ферм; д) комбинированных систем?
Как соответственно формируется матрица В?
8. Как в матрицах L, B и LF учитывается наличие в системе упругоподатливых
связей?
9. Из каких частей (блоков) состоят матрицы L0, B0 и L ? ( 2 )

12.

Контрольные вопросы
См. тему «Матричная
форма определения
перемещений линейно
деформируемых систем»
( в скобках даны номера слайдов, в которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 22» )
10. Какую структуру (поблочно) и размеры (число строк и столбцов) имеют
матрицы Lt , Bt и T ?
11. Значения каких величин и в какой последовательности приводятся
в матрицах Lt и T ?
12. Какие характеристики расчётных участков используются при формировании матрицы температурной податливости Bt ?
13. Какие размеры (число строк и столбцов) имеют матрицы Rc и c ?
Из значений каких величин формируются эти матрицы и как согласуются
последовательности записи их компонентов?
14. Матричные формулы для вычисления искомых силовых факторов:
а) в характерных сечениях (расчётных сечениях расчётных участков ОСМС) ( 3 ) ;
б) в требуемом наборе (в том числе в произвольно назначенных сечениях) ( 3 ) .
15. Сколько и каких исходных матриц (перечислить) необходимо составить для выполнения расчёта с результатами по вариантам (а) и (б) предыдущего вопроса? ( 3 ) , ( 4 )
16. Что получается в результате выполнения следующих матричных операций:
а) Lтi B Lk ?; б) Lт B L ? ; в) Lтi B LF ? ; г) Lт B LF ? ; д) Lтt Bt T ? ; е) Rcт E Δc ? ; ж) Lт0 B0 LΣ ?;
з) (Lт B L ) 1 (Lт0 B0 LΣ) ? ; и) (Lт B L ) 1 (Lт B LF ) ? ; к) (Lт B L ) 1 (Lтt Bt T) ?;
(2)
л) (Lт B L ) 1 (Rcт E Δc ) ?;
(3)
м) L*Σ L (Lт B L ) 1 (Lт0 B0 LΣ) ? ; н) L~*Σ L~ (Lт B L ) 1 (Lт0 B0 LΣ) ?;
о) LF L (Lт B L ) 1 (Lт B LF ) ?; п) L~F L~ (Lт B L ) 1 (Lт B LF ) ?.
17. Формулы кинематической проверки (универсальной и раздельной) в матричной форме
при силовых, температурных и кинематических воздействиях ( 7 ) .
*) Только в режиме «Показ слайдов».