Лекция 4(сгм) — 24-25

1. Специальные главы математики

Лекция 4
Равномерная сходимость степенных
рядов. Ряды Фурье.

2.

§ 6. Равномерная сходимость функциональных
рядов
Рассмотрим функциональный ряд
Пусть ряд сходится на некотором множестве D, тогда
его сумма
для каждого х D.
При х = х1 (х1 D) можно решать задачу
приближенного нахождения S(х1) Sn(х1), а именно
> 0 ( −погрешность приближения) можно указать
номер n1 = n1( ) такой, что при n n1 |S(х1) − Sn(х1)| < ,
т.е. S(х1) Sn(х1) с погрешностью .
2

3.

В другой точке х = х2 (х2 D), по той же погрешности
приближение S(х2) Sn(х2), реализуется (в общем
случае) для другого n2 (n1 n2).
Множество D может содержать бесконечное
множество точек {х1, х2, х3…}, для каждой из них по
одному и тому же > 0 находится свой номер nk с
указанными свойствами.
Это означает, что функция Sn(х) не является
приближением суммы функционального ряда
на множестве D с погрешностью .
3

4.

Определение 1 (поточечная сходимость).
Функциональный ряд
сходится к функции S(x)
на множестве D, если
x D 0 N
n : n N S x Sn x
Определение 2 (равномерная сходимость).
Функциональный ряд
равномерно сходится к
функции S(x) на множестве D, если
0 N ( )
x D n : n N S x Sn x
4

5.

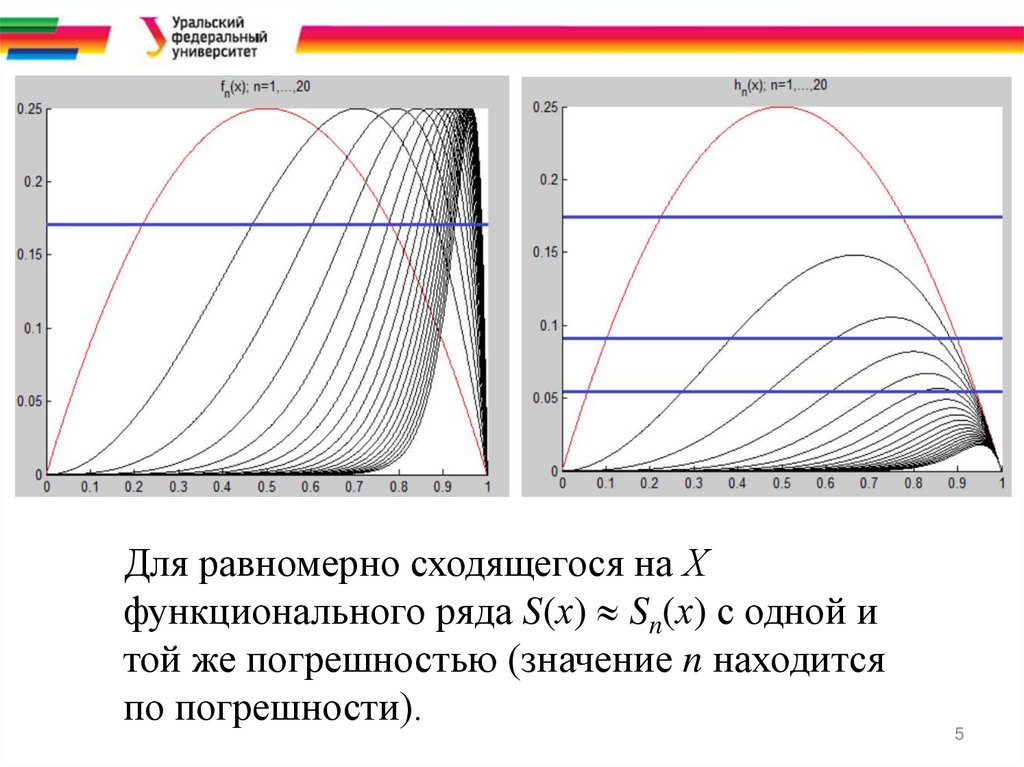
Для равномерно сходящегося на Х
функционального ряда S(х) Sn(х) с одной и
той же погрешностью (значение n находится
по погрешности).
5

6.

Теорема (признак Вейерштрасса)
Если для
х D , существует числовой ряд
такой, что 1) n: an>0; 2) n, х D : |un(x)| an;
3)
− сходится, то
равномерно сходится к
S(x) на множестве D, где
Числовой ряд
называется мажорантой для
функционального ряда
, а сам функциональный
ряд называется мажорируемым на D.
6

7.

Пример. Доказать, что ряд сходится равномерно на
промежутке [1,+∞)
1 nx4x 2
n 1
7

8.

Равномерная сходимость степенного ряда
Ґ
Пусть е an x n сходится к S(х) на D = (−R; R). Возьмем
n= 0
х1 D. Тогда ряды
Для всех х, |x| |x1| ряд
и
сходятся.
является мажорантой.
По признаку Вейерштрасса исходный ряд равномерно
сходится на [−|x1|; |x1|].
Т.о. всякий степенной ряд, сходящийся на (−R; R),
равномерно сходится на любом отрезке, вложенном в
интервал сходимости.
8

9.

Свойства равномерно сходящихся степенных рядов:
1. Сумма S(x) степенного ряда является непрерывной
функцией в интервале сходимости.
2. Степенной ряд можно почленно интегрировать в
интервале сходимости:
(−R<a<t<R).
3. Степенной ряд можно почленно дифференцировать в
интервале сходимости:
После интегрирования и дифференцирования
полученные ряды имеют тот же радиус сходимости.
9

10.

§ 7. Периодические функции. Ряды Фурье
Функция называется периодической с периодом Т>0
(или Т − периодической), если для всех значений x Х
выполняется равенство f(x+T)=f(x).
Простейшими периодическими функциями являются
простые гармоники:
где |A|−амплитуда, ω− частота, φ0− начальная фаза.
В механике такая функция описывает гармонические
колебания точки, у которой период колебаний равен
2π/ω.
10

11.

Преобразуем эту функцию к виду
Таким образом, простая гармоника имеет вид:
При наложении простых гармоник получается
сложное гармоническое колебание, которое
описывается функцией вида
11

12.

При неограниченном возрастании n получим ряд,
который обычно записывают в виде
и называют тригонометрическим рядом; числа a0, an, bn
называют коэффициентами ряда.
Если ряд сходится, то его сумма S(x) является
2π/ω−периодической функцией.
12

13.

Пусть f(x) произвольная периодическая функция с
периодом 2l. Предположим, что f(x) разлагается в
тригонометрический ряд, т.е. является его суммой:
Так как сумма является 2π/ω − периодическая функция,
то 2l=2π/ω и ω=π/l.
Если равенство (1) выполняется во всех точках
непрерывности функции f(x), то ряд, стоящий в правой
части этого равенства, называется рядом Фурье
функции f(x), а сама функция называется разложимой
в ряд Фурье.
13

14.

Теорема 1 (Дирихле).
Если 2l−периодическая функция f(x) является кусочномонотонной и ограниченной на отрезке [−l; l], то:
1) функция f(x) разложима в ряд Фурье;
2) в каждой точке x0 разрыва функции сумма ряда
Фурье S(x) равна среднему арифметическому пределов
функции f(x) слева и справа, т.е.:
3) ряд Фурье можно почленно интегрировать.
14

15.

Теорема 2 (о коэффициентах ряда Фурье).
Если функция удовлетворяет условиям теоремы
Дирихле, то коэффициенты её ряда Фурье вычисляются
по формулам:
Коэффициенты a0, an, bn, определяемые по этим
формулам, называются коэффициентами Фурье.
Замечание. Иногда удобно вычислять интегралы в
указанных формулах не по отрезку [−l; l], а по другому
промежутку длиной 2l (в силу свойства периодических
функций).
15

16.

Пример. Разложить в ряд Фурье функцию f(x)=x,
x [0; 2 ], T= 2 . Построить график суммы ряда.
16

17.

Разложение в ряд Фурье чётных и нечётных функций
По свойствам определенных интегралов
если f(x)−нечетная функция;
если f(x)−четная функция.
18

18.

Пусть в ряд Фурье на отрезке [−l; l] раскладывается
нечётная функция f(x).
Тогда коэффициенты ряда Фурье вычисляются
следующим образом:
Таким образом, ряд Фурье для нечётной функции
будет иметь вид:
19

19.

Если в ряд Фурье на отрезке [−l; l] раскладывается
чётная функция f(x), то коэффициенты ряда Фурье
вычисляются следующим образом:
20

20.

Следовательно, ряд Фурье для чётной функции будет
иметь вид:
Ряды (2) и (3) называются неполными
тригонометрическими рядами или рядами по синусам
и косинусам соответственно.
21

21.

Пример. Разложить в ряд Фурье функцию f(x)=x,
x [−2; 2], T= 4.
22

22.

Разложение в ряд Фурье функции,
заданной на отрезке
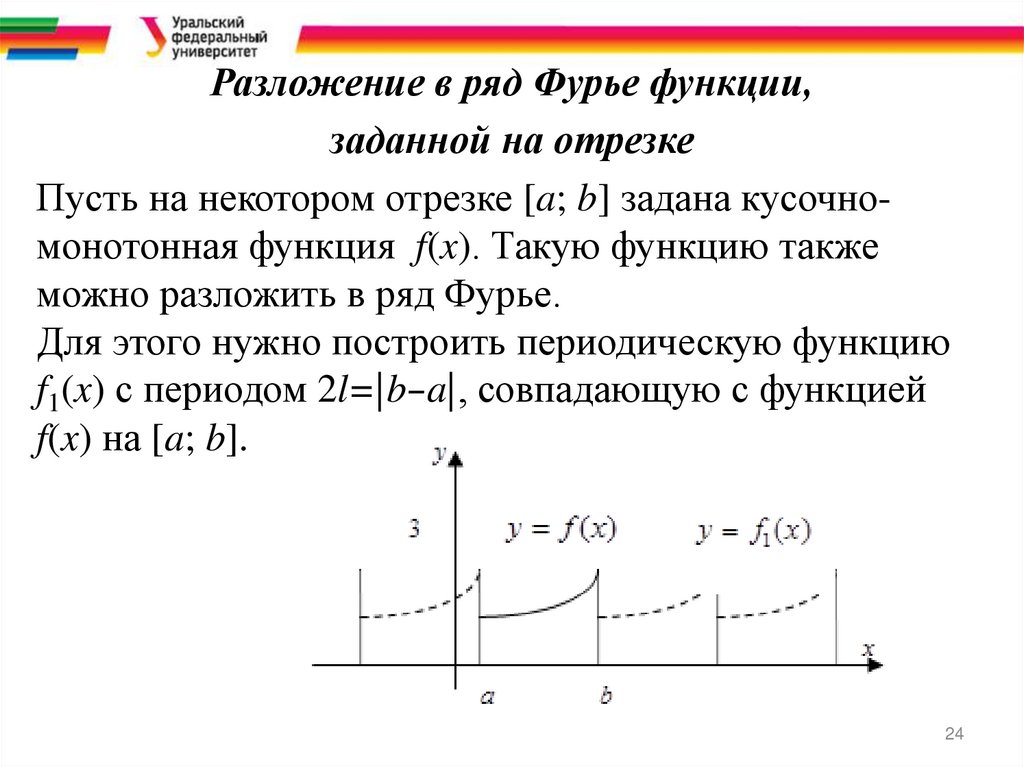
Пусть на некотором отрезке [a; b] задана кусочномонотонная функция f(x). Такую функцию также
можно разложить в ряд Фурье.
Для этого нужно построить периодическую функцию
f1(x) с периодом 2l=|b−a|, совпадающую с функцией
f(x) на [a; b].
24

23.

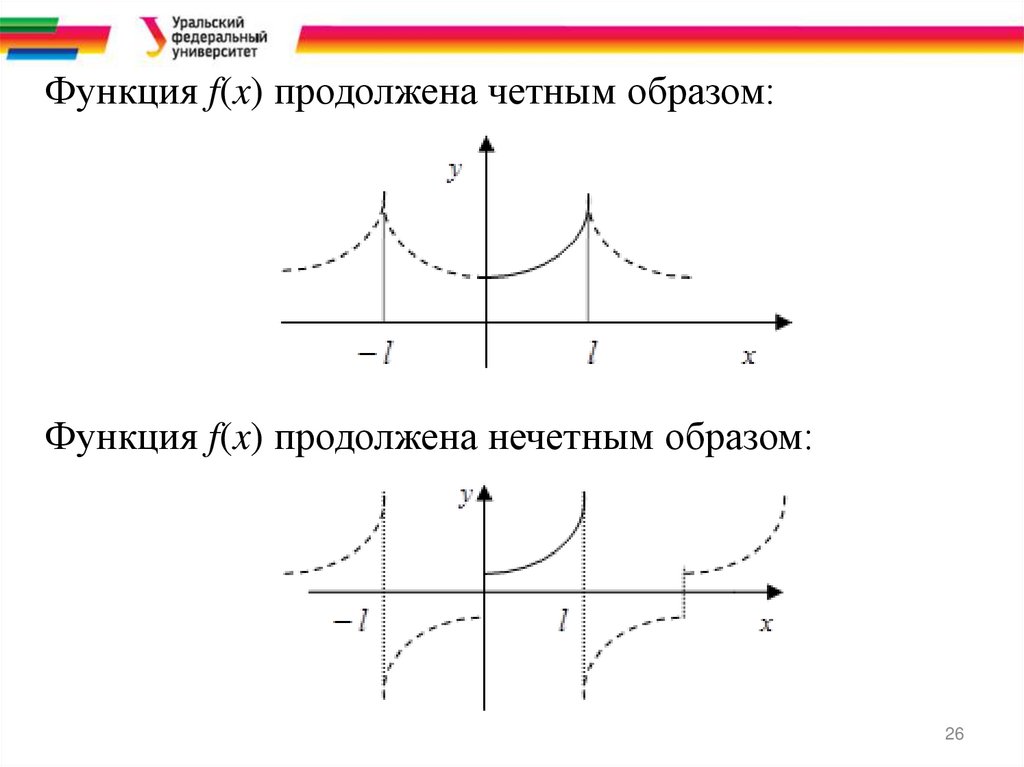
Если функция задана на отрезке [0; l], то:
а) функцию можно продолжить периодически с
периодом T=l; тогда ряд Фурье для f(x) будет иметь
вид (1);
б) функцию можно продолжить чётным образом на
отрезок [−l; 0]; тогда ряд Фурье для f(x) будет
содержать только косинусы и иметь вид (3);
в) функцию можно продолжить нечётным образом на
отрезок [−l; 0]; тогда ряд Фурье для f(x) будет
содержать только синусы и иметь вид (2).
25

24.

Функция f(x) продолжена четным образом:
Функция f(x) продолжена нечетным образом:
26

25.

Пример. Разложить в ряд Фурье функцию f(x)=x,
x [0; 2], продолжив ее четным образом.
27