Презентация лекции №2 по теме Магнетизм (2)

1. Магнитное поле

I.
II.
III.
IV.
V.
VI.
VII.
Вихревой характер магнитного поля.
Циркуляция вектора магнитной индукции
Закон полного тока
Магнитный поток
Теорема Остроградского – Гаусса для
магнитного поля
Работа перемещения проводника и контура с
током в магнитном поле
Сила Лоренца
Эффект Холла

2. Вихревой характер магнитного поля

Магнитное поле создается
прямолинейным
проводником с током.
L – замкнутый контур
(может быть произвольной
формы).
d l – элементарный вектор
длины контура L,
направленный вдоль обхода
контура

3. Вихревой характер магнитного поля

Циркуляцией вектора
магнитной индукции
вдоль замкнутого
контура называется
интеграл вида
B d l B d l cos B d l
L
L

4. Закон полного тока для магнитного поля в вакууме

Циркуляция вектора индукции магнитного
поля вдоль замкнутого контура в вакууме
пропорциональна алгебраической сумме
токов, охватываемых этим контуром
n
B d l 0 I i
L
i 1
где n – число проводников с токами,
охватываемых контуром L произвольной
формы.

5. Закон полного тока для магнитного поля в вакууме

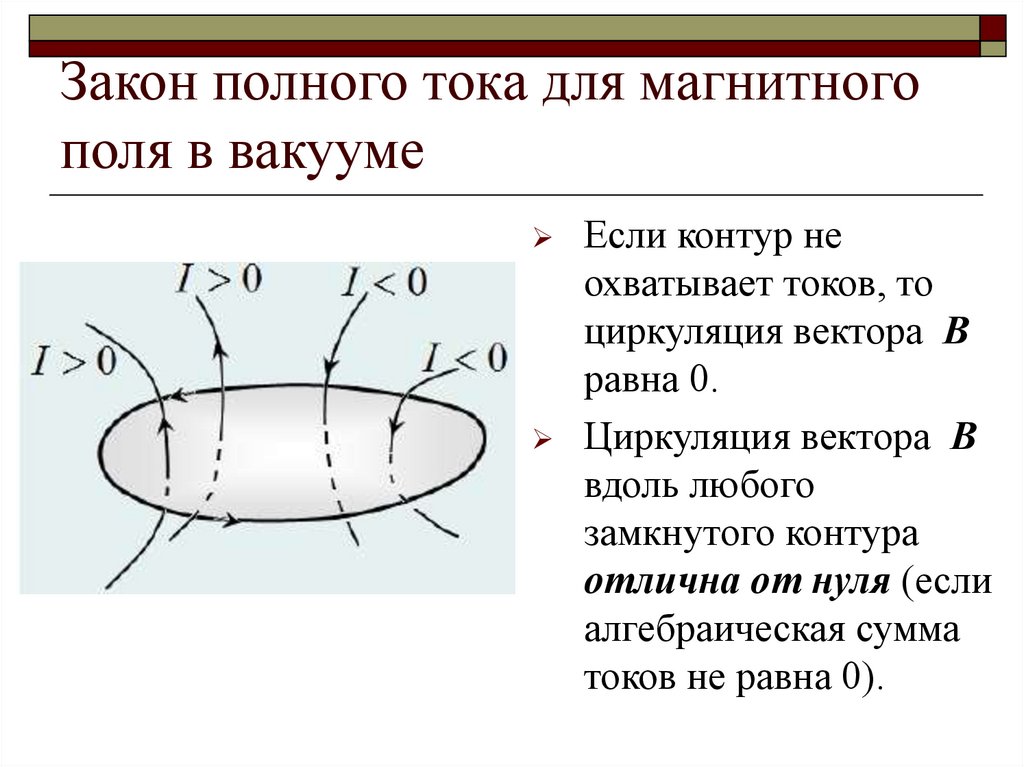
Если контур не
охватывает токов, то
циркуляция вектора В
равна 0.
Циркуляция вектора В
вдоль любого
замкнутого контура
отлична от нуля (если
алгебраическая сумма
токов не равна 0).

6. Вычисление магнитной индукции поля бесконечно длинного соленоида

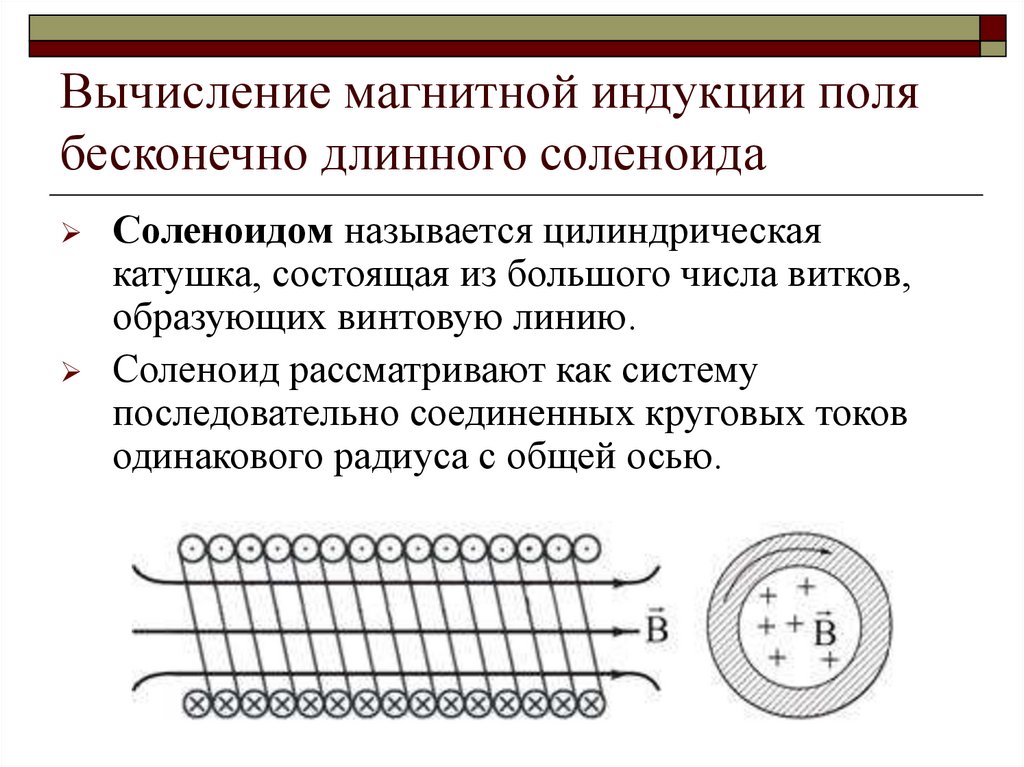
Соленоидом называется цилиндрическая
катушка, состоящая из большого числа витков,
образующих винтовую линию.
Соленоид рассматривают как систему
последовательно соединенных круговых токов
одинакового радиуса с общей осью.

7. Вычисление магнитной индукции поля бесконечно длинного соленоида

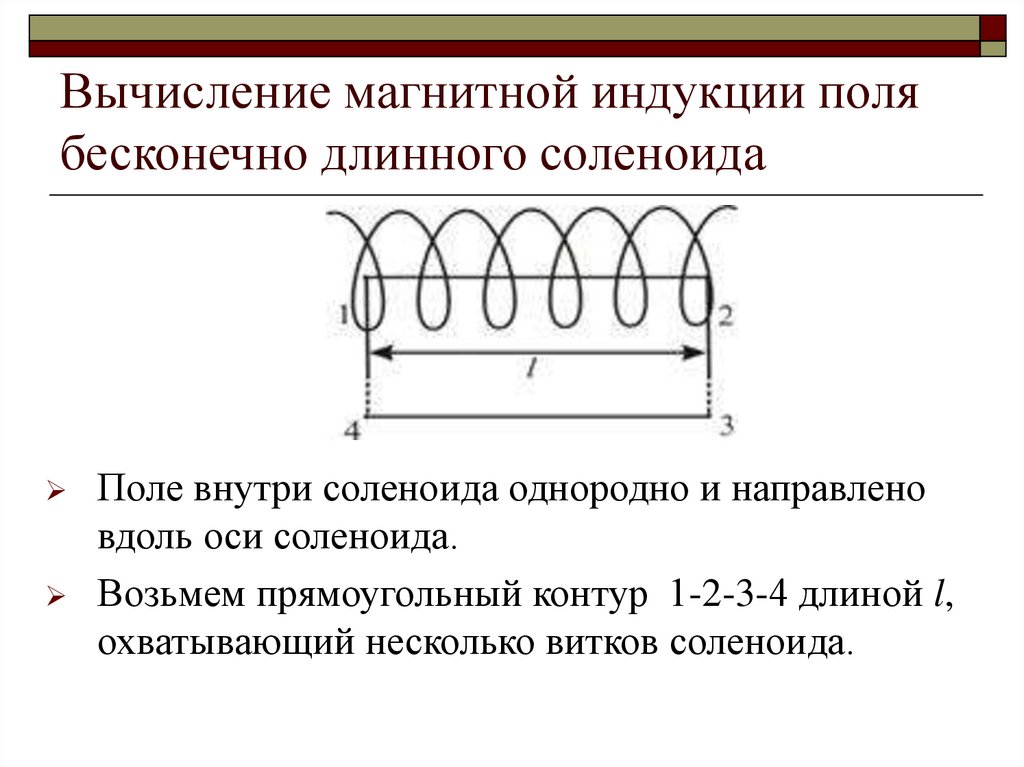
Поле внутри соленоида однородно и направлено
вдоль оси соленоида.
Возьмем прямоугольный контур 1-2-3-4 длиной l,
охватывающий несколько витков соленоида.

8. Вычисление магнитной индукции поля бесконечно длинного соленоида

Циркуляцию вектора магнитной индукции В по
этому контуру можно представить в виде
2
3
4
1
B d l Bl d l Bl d l Bl d l Bl d l Bl d l
L
L
1
2
3
Bl – проекция вектора В на направление l .
4

9. Вычисление магнитной индукции поля бесконечно длинного соленоида

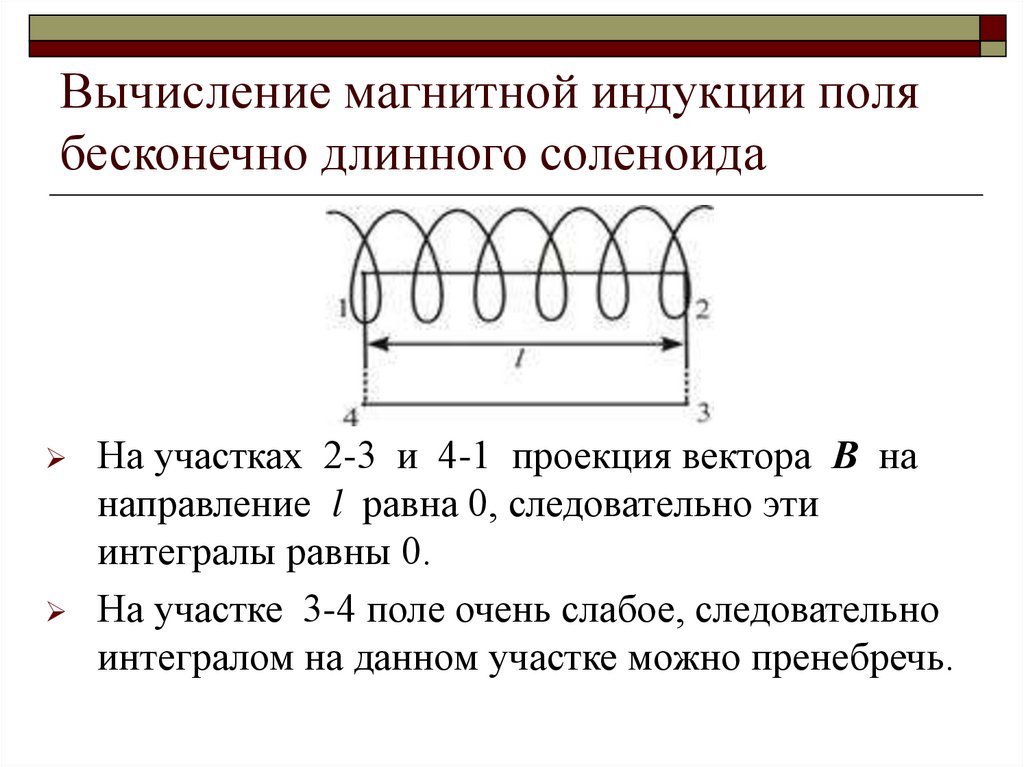
На участках 2-3 и 4-1 проекция вектора В на
направление l равна 0, следовательно эти
интегралы равны 0.
На участке 3-4 поле очень слабое, следовательно
интегралом на данном участке можно пренебречь.

10. Вычисление магнитной индукции поля бесконечно длинного соленоида

Следовательно
2
B d l Bl d l Bl d l Bl
L
L
1
Применяя закон полного тока, имеем
N
Ii 0 Nl I
Bl d l B l 0
i 1
L
N – число витков соленоида.

11. Вычисление магнитной индукции поля бесконечно длинного соленоида

Т.о. внутри бесконечно длинного соленоида
магнитная индукция одинакова и
определяется формулой
B = μ0 n I
Величина n I называется числом ампервитков на метр.
Вне соленоида магнитная индукция равна 0.

12. Контур с током в магнитном поле

В
Плоский замкнутый
проводящий контур с током
произвольной геометрической
формы, помещенный в
однородное магнитное поле,
испытывает действие
вращающего момента
М = [ Pm B ]
Pm – вектор магнитного
момента контура с током.

13. Контур с током в магнитном поле

Вращающий момент направлен перпендикулярно
к плоскости, образованной векторами Pm и B .
Момент М стремится повернуть контур так,
чтобы его магнитный момент Pm совпадал по
направлению с B .

14. Магнитный поток

Потоком вектора
магнитной индукции
(магнитным потоком)
сквозь малую поверхность
dS называется скалярная
физическая величина
dФm = B dS,
где dS = n dS
или
dФm = B dS cos (B^n)

15. Магнитный поток

Магнитный поток dФ сквозь
произвольную замкнутую поверхность S
Ф m B d S Bn d S
S
S
Если поле однородное, а поверхность
плоская и расположена перпендикулярно
полю, то
Фm = B S

16. Теорема Остроградского –Гаусса для магнитного поля.

Магнитный поток сквозь произвольную
замкнутую поверхность равен 0.
Ф m B d S Bn d S 0
S
S
Эта теорема является математическим
выражением того, что в природе не
существует магнитных зарядов, на которых
начинались бы или заканчивались линии
магнитной индукции.

17. Работа перемещения проводника и контура с током в магнитном поле

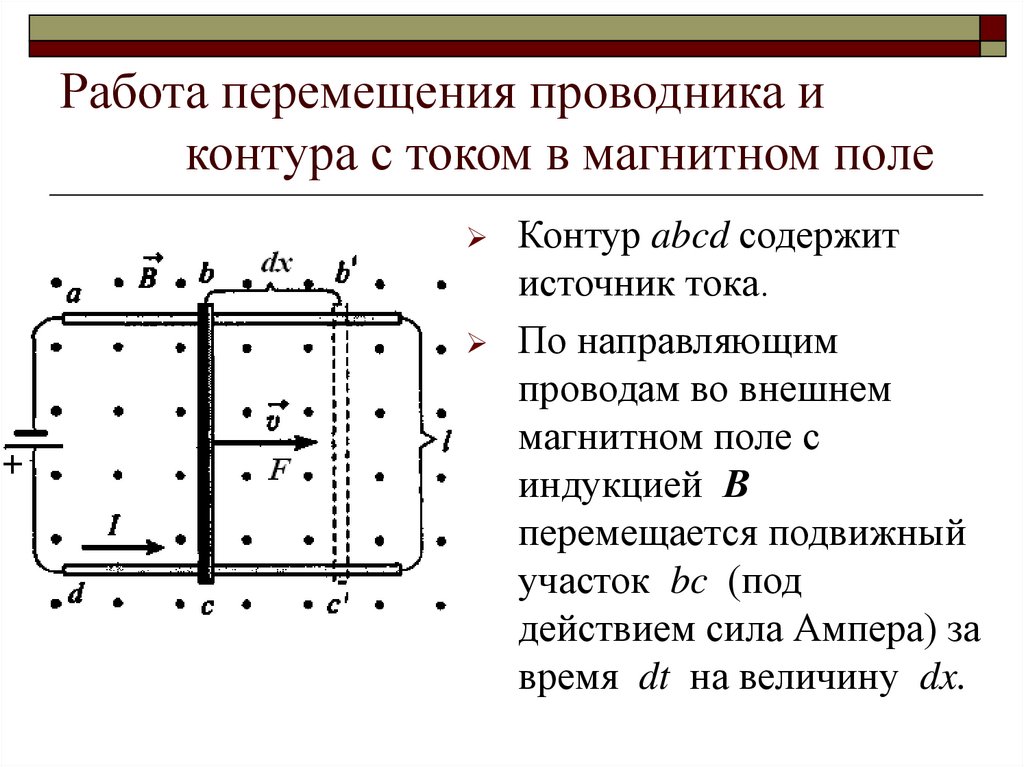
Контур abcd содержит
источник тока.
По направляющим
проводам во внешнем
магнитном поле с
индукцией В
перемещается подвижный
участок bc (под
действием сила Ампера) за
время dt на величину dx.

18. Работа перемещения проводника и контура с током в магнитном поле

Совершаемая при этом элементарная работа
dA = FAdx = I B l dx= I B dS = I dФm
Работа, совершаемая силами Ампера при
перемещении в магнитном поле замкнутого
плоского контура с постоянным током из начального
положения в конечное
А12 = I (Фm2 – Фm1)
Работа совершается за счет источника,
поддерживающего постоянным ток в контуре.

19. Сила Лоренца

Сила, действующая на
электрический заряд q ,
движущуюся в магнитном
поле со скоростью v,
называется силой Лоренца
и она равна
FЛ = q [ v B ]
В скалярной форме
FЛ = q v B sinα
α - ( v^B)

20. Сила Лоренца

Направление силы Лоренца
для положительно
заряженной частицы
определяется по правилу
левой руки.
Для отрицательно
заряженной частицы
направление силы Лоренца
берется противоположным.

21. Сила Лоренца

Если скорость заряженной частицы q
перпендикулярна вектору магнитной индукции В ,
то частица будет двигаться по окружности
радиусом R.
Сила Лоренца уравновешивается
2
mv
центростремительной силой
qv B
R
Радиус окружности
mv
R
qB

22. Сила Лоренца

Если вектор скорости
заряженной частицы
составляет некоторый
угол с направлением
вектора индукции
магнитного поля, то
частица будет двигаться
по винтовой линии.
h – шаг спирали.

23. Эффект Холла

Эффект Холла заключается в том, что в металле или
полупроводнике с током, помещенных в магнитное
поле, перпендикулярное вектору плотности тока j,
возникает поперечное электрическое поле и
разность потенциалов.
Причиной является отклонение электронов,
движущихся в магнитном поле, под действием силы
Лоренца.