Similar presentations:
2_1 Производная25+
1.
Раздел 2. ДИФФЕРЕНЦИАЛЬНОЕИСЧИСЛЕНИЕ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ
§ 1. Производная функции
Пусть функция y = f (x) определена на некотором интервале
(a; b). Выберем точку x0 (a; b). Выберем другую точку
x = x0 + Δx (a; b).
Величина Δx = x - x0 называется приращением аргумента.
Найдем
соответствующее
Δy = f (x0 + Δx) – f (x0).
приращение
функции
2.
Опр.1. Производной f ′ (x0) функции y = f (x) в точке x0называется предел отношения приращения функции ∆y к
приращению аргумента Δx при Δx 0, если этот предел
существует и конечен:
f x0 x f x0
y
lim
.
x 0 x
x 0
x
f x0 lim
Обозначения: f x0 , y x0 , y , y x , (ввел Ж.Л. Лагранж,
предложил термин «производная»
dy df x (ввел Г.В. Лейбниц,
,
,
dx dx
предложил термин «дифференциал»)
y. (ввел И. Ньютон,
это обозначается употребляется теперь в механике,
когда независимой переменной является время.)
3.
WWWВИКИСПРАВКАWWWWWWWWWWWWWWWWWWЖозе́ф Луи́ Лагра́нж
(фр. Joseph Louis Lagrange,
итал. Giuseppe Lodovico Lagrangia)
(1736–1813)
французский математик, астроном и механик итальянского
происхождения. Наряду с Эйлером – крупнейший
математик XVIII в. Внес огромный вклад в математический
анализ, теорию чисел, теорию вероятностей и численные
методы, создал вариационное исчисление. В классическом
трактате
«Аналитическая
механика»
установил
фундаментальный
«принцип возможных перемещений» и завершил математизацию механики.
Прославился исключительным мастерством в области обобщения и синтеза
накопленного научного материала. Пьер-Симон Лаплас дал такую
характеристику деятельности Лагранжа: «…среди тех, кто самым эффективным
образом раздвинул пределы наших знаний, Ньютон и Лагранж в самой высокой
степени владели счастливым искусством открывания новых данных,
представляющих собой существо знаний…».
Имя Лагранжа внесено в список 72 величайших ученых Франции, помещенный
на первом этаже Эйфелевой башни.
WWWWWWWWWWWWWWWWWWWWWWWWWWWWWWW
4.
WWWВИКИСПРАВКАWWWWWWWWWWWWWWWWWWГо́тфрид Ви́льгельм Ле́йбниц
(нем. Gottfried Wilhelm von Leibniz)
(1646 – 1716)
саксонский философ, логик, математик, механик,
физик, юрист, историк, дипломат, изобретатель и
языковед. Основатель и первый президент Берлинской
Академии наук. В 1682 г. основал научный журнал «Acta
Eruditorum»,
способствовавший
распространению
научных знаний в Европе.
Независимо от Ньютона создал математический анализ
– дифференциальное и интегральное исчисления,
основанные
на бесконечно малых. Ввел термины «дифференциал», «дифференциальное
исчисление», «дифференциальное уравнение», «функция», «переменная»,
«координаты», «алгоритм».
Заложил основы математической логики, создал комбинаторику как науку, описал
двоичную систему счисления с цифрами 0 и 1. Ввел термин «модель», писал о
возможности моделирования функций человеческого мозга.
Изобрел собственную конструкцию арифмометра, который мог выполнять
умножение, деление, извлечение квадратных и кубических корней, возведение в
степень. Описал проект вычислительной машины, работающей в двоичной
системе счисления, в которой использовался прообраз перфокарты.
WWWWWWWWWWWWWWWWWWWWWWWWWWWWWWW
5.
WWWВИКИСПРАВКАWWWWWWWWWWWWWWWWWWГо́тфрид Ви́льгельм Ле́йбниц
(нем. Gottfried Wilhelm von Leibniz)
(1646 – 1716)
саксонский философ, логик, математик, механик,
физик, юрист, историк, дипломат, изобретатель и
языковед.
Трижды встречался с Петром I, по просьбе которого
разработал ряд проектов развития образования и
государственного управления в России. Эти встречи
побудили Петра к созданию Академии наук в
Петербурге.
Лейбниц считал, что успех алгебры объясняется
искусством
пользоваться символами, необходимо выбирать удобные обозначения,
выражающие сущность вещей – тогда сокращается работа мысли.
Лейбниц считается одним из самых всеобъемлющих гениев за всю историю
человечества. Дени Дидро в «Энциклопедии» отметил, что для Германии
Лейбниц был тем, чем для Древней Греции были Платон, Аристотель и
Архимед вместе взятые. Норберт Винер говорил, что, если бы ему
предложили выбрать святого – покровителя кибернетики, то он выбрал бы
Лейбница.
6.
WWWВИКИСПРАВКАWWWWWWWWWWWWWWWWWWВ 1708 г. вспыхнул печально
известный спор Лейбница и Ньютона о
научном
приоритете
в
открытии
дифференциаль-ного
исчисления.
Лейбниц и Ньютон работали над
дифференциальным
исчислением
параллельно, Лейбниц был знаком с
некоторыми
неопубликован-ными
работами и письмами Ньютона, но
пришёл
к
тем
же
результатам
самостоятельно. Известно, что Ньютон
создал свою версию математического
Го́тфрид Ви́льгельм
Исаа́к Нью́то́н
анализа, «метод флюксий» (термин
Ле́йбниц
Ньютона
«флюксия»
соответствует (англ. Isaac Newton)
(нем. Gottfried Wilhelm термину «производная»), не позднее
(1642—1727)
von Leibniz)
1665 г., хотя опубликовал лишь после
(1646 – 1716)
1704 г.; Лейбниц завершил создание
своего «исчисления бесконечно малых» к
1675 г., и первым в 1684 г. опубликовал работу «Новый метод максимумов и минимумов…»,
разработав символику, которая оказалась настолько удобной, что её используют и сейчас.
Отмечая практическую полезность и простоту нового метода, Лейбниц писал: «То, что
человек, сведущий в этом исчислении, может получить прямо в трёх строках, другие
учёнейшие мужи принуждены были искать, следуя сложными обходными путями».
WWWWWWWWWWWWWWWWWWWWWWWWWWWWWWW
7.
Пример 1. Вычислим производные по определению:1) y = c (постоянная, число)
∆y = y(x + ∆x) – y(x) = c – c = 0
y
0
c lim
lim
0
x 0 x
x 0 x
2) y = x
∆y = y(x + ∆x) – y(x) = (x + ∆x) –
∆x.
y
x x =
x lim
lim
1
x 0 x
x 0 x
3) y = x2
2
2
∆y = y(x + ∆x) – y(x) = ( x x) x 2 x x ( x)2
2 x x ( x)
y
lim (2 x x) 2 x
lim
x lim
x 0
x 0
x 0 x
x
2
2
4) y = ex
∆y = y(x + ∆x) – y(x) = ex + x – ex
x
x
y
e x x e x
e
1
e
1 x e x lim x e x
0
x
lim
e lim
e lim
x 0 x
x 0
0 x 0
x 0 x
x 0 x
x
x
8.
Если f ′ (x0) не существует, то часто рассматривают односторонниепроизводные f ′ (x0 - 0) и f ′ (x0+0 ).
Если существует
то он называется правой производной функции y = f (x) в точке
x0 и обозначается f ′ (x0+0 ) или f ′+ (x0 ) или f ′прав (x0).
Если существует
то он называется левой производной функции y = f (x) в точке x0 и
обозначается f ′- (x0 ) или f ′лев (x0).
Функция y = f (x) может иметь в точке x0 не равные односторонние
пределы.
9.
Опр.2. Функция y = f (x), определенная в некоторойокрестности B(x0) точки x0, называется дифференцируемой в
точке x0, если ее приращение ∆y представимо в виде
∆y = A∙∆x + (∆x), где ∆x – приращение аргумента, вызвавшее
приращение функции ∆y; A – постоянная (т. е. величина, не
зависящая от ∆x); (∆x) = o(∆x) – б. м. ф. более высокого порядка
малости, чем ∆x при ∆x → 0, т. е. lim x 0.
x
Тh. (Необходимое условие дифференцируемости функции.) Если
x 0
функция дифференцируема в точке x0, то она непрерывна в этой
точке.
y
Доказательство. Так как функция дифференцируема, f ( x0 ) lim .
x 0
y
f ( x0 ) x y f ( x0 ) x x x, x 0 y 0
x
x
функция непрерывна в точке. ◄
Доказано.
Обратное утверждение неверно, т. е. если функция
непрерывна в точке, то она может быть не дифференцируемой в
этой точке.
10.
x, x 0,Например, функция y x
x, x 0
непрерывна, но не дифференцируема в
точке x = 0.
y f 0 x f 0 f x x
.
x
x
x
x
y lim x 1;
x 0
f x0 0 lim
x 0 x
x
x
0
x 0
x
y
lim
1;
x 0
x 0 x
x
x 0
x 0
f x0 0 lim
Производная в точке x = 0 не существует.
Опр. 3. Функция, имеющая конечную производную в точке,
называется дифференцируемой в этой точке, а операция
нахождения производной называется дифференцированием.
11.
Т2 (о связи дифференцируемости и производной).Функция y = f (x) дифференцируема в точке x0
она имеет в этой
точке конечную производную f ′ (x0) = A.
⇔
Доказательство. 1) ⇒
Т. к. функция дифференцируема, то ∆y = A∆x + o(∆x)
o( x)
A x o( x)
y
lim A
f x0 lim
lim
A.
x 0
x 0 x
x 0
x
x
y
2) ⇐ Если существует конечная производная f x0 lim
A,
x 0 x
то по теореме о связи между функцией, ее пределом и б.м.ф.
y
где lim α( x) 0
A α( x),
x 0
x
y A x α( x) x A x o( x).
Доказано.
Следовательно, дифференциал равен
dy(x0) = f ′ (x0) dx.
!
!
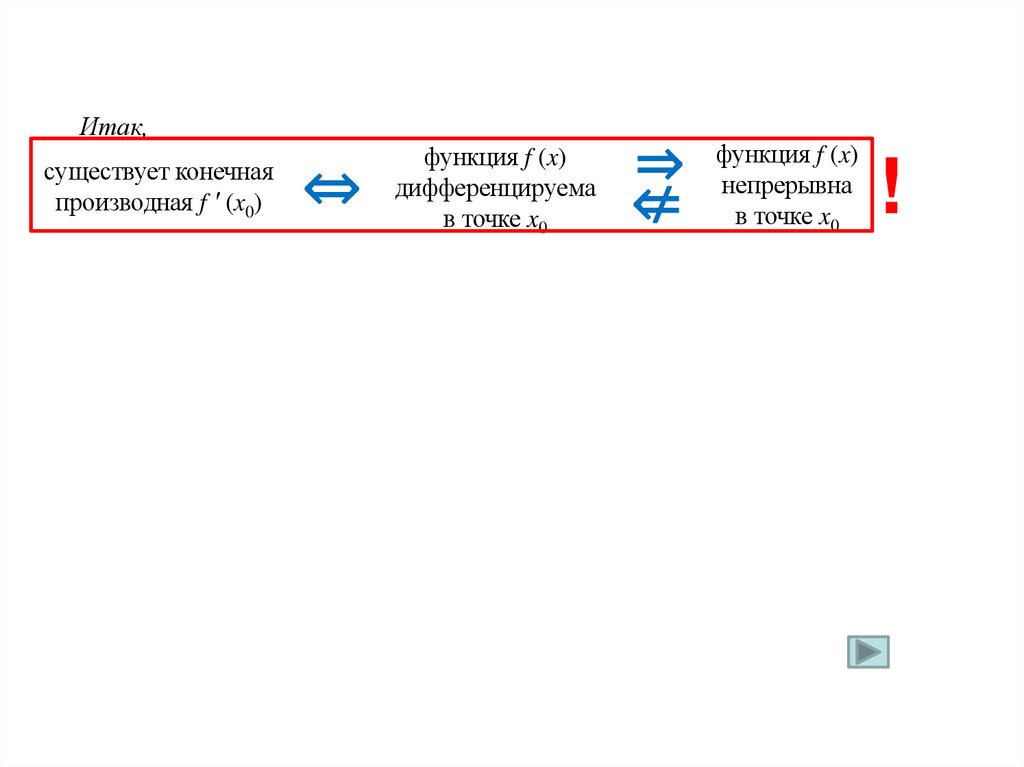
12.
Итак,существует конечная
производная f ′ (x0)
⇔
функция f (x)
дифференцируема
в точке x0
f (x)
⇒ функция
непрерывна
⇍ в точке x !
0
13.
§ 2. Физический и геометрическийсмысл производной
Пусть материальная точка движется по прямой в одном
направлении по закону s = f (t), где t – время, а s – путь,
пройденный за время t.
Задача определить скорость v0 материальной точки в момент t0.
Рассмотрим другой момент времени t = t0 + ∆t.
Тогда за промежуток времени ∆t = t – t0 точка прошла путь
s
v
∆s = s – s0 = f (t0 + ∆t) – f (t0). ср
t
Мгновенная скорость v(t0) - предел средней скорости vср при
∆t → 0, т. е. v t lim s lim f t0 t f t0 .
0
t 0 t
t 0
t
Если S = S(t) – закон прямолинейного движения точки, то
S′(t0) = V(t0) – скорость движения в момент времени t0.
В
общем
случае
производную
функции
интерпретировать как «скорость» изменения функции.
можно
14.
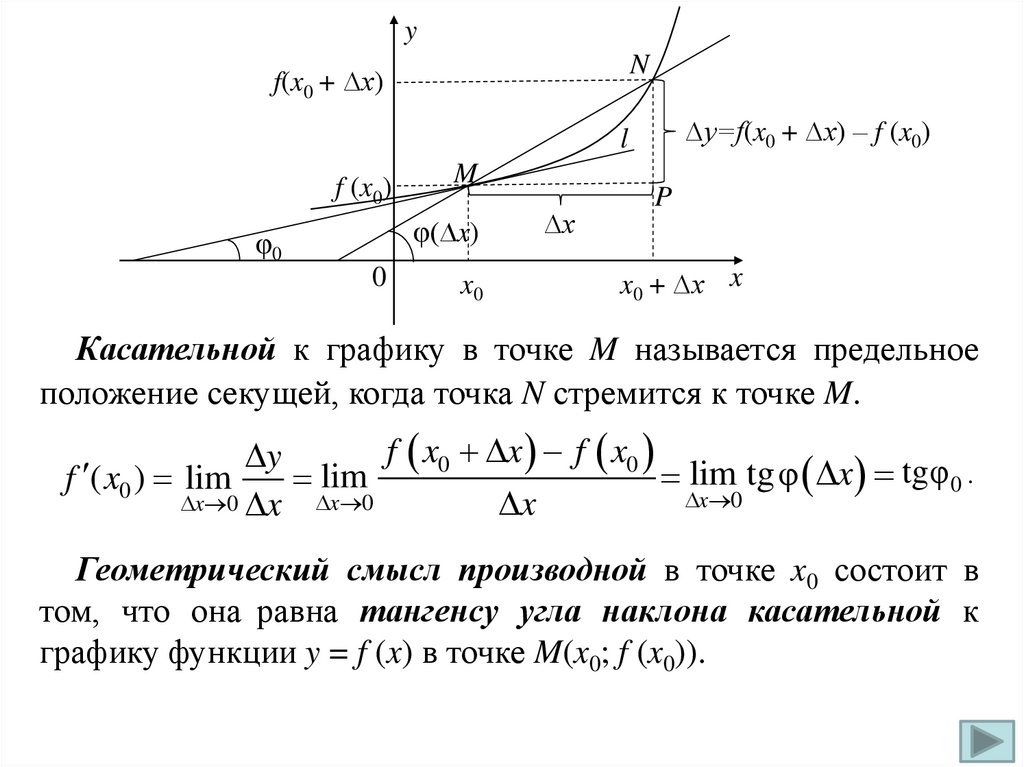
yN
f(x0 + ∆x)
∆y=f(x0 + ∆x) – f (x0)
l
f (x0)
M
φ(∆x)
φ0
0
x0
∆x
P
x0 + ∆x x
Касательной к графику в точке M называется предельное
положение секущей, когда точка N стремится к точке M.
f x0 x f x0
y
lim tgφ x tgφ 0 .
f ( x0 ) lim
lim
x 0
x 0 x x 0
x
Геометрический смысл производной в точке x0 состоит в
том, что она равна тангенсу угла наклона касательной к
графику функции y = f (x) в точке M(x0; f (x0)).
15.
Получим уравнение касательной:k = f ′(x0), y = kx + b:
f ( x0 ) f ( x0 ) x0 b b f ( x0 ) f ( x0 ) x0 ;
y f ( x0 ) x f ( x0 ) f ( x0 ) x0
Уравнение касательной к графику функции y = f (x) в точке
M(x0; f (x0)) имеет вид y = f (x0) + f ′(x0)(x – x0).
Нормалью к графику функции y = f (x) в точке M0(x0; f (x0))
называется прямая, проходящая через точку M0 и
перпендикулярная касательной к графику в этой точке.
Пусть γ – угол наклона нормали, γ α 900.
kнорм tgγ tg α 900 ctgα
y
M0
f (x0)
γ
x0
Нормаль
Касательная
α
x
1
1
.
f x0
kкас
Уравнение нормали к графику
(кривой) в точке (x0; f (x0)) в случае
f ′(x0) ≠ 0 имеет вид:
y f ( x0 )
1
( x x0 ).
f ( x0 )
16.
Замечание. В случае бесконечной производнойи
2
уравнение касательной имеет вид x = x0, уравнение нормали
y = f (x0), т. е. касательная параллельна оси Oy, а нормаль оси
Ох. Если f ′(x0) = 0, то касательная параллельна оси Ох и ее
уравнение y = f (x0), уравнение нормали тогда x = x0.
Нормалью к графику функции y = f (x) в точке M0(x0; f (x0))
называется прямая, проходящая через точку M0 и
перпендикулярная касательной к графику в этой точке.
Пусть γ – угол наклона нормали, γ α 900.
kнорм tgγ tg α 900 ctgα
y
M0
f (x0)
γ
x0
Нормаль
Касательная
α
x
1
1
.
f x0
kкас
Уравнение нормали к графику
(кривой) в точке (x0; f (x0)) в случае
f ′(x0) ≠ 0 имеет вид:
y f ( x0 )
1
( x x0 ).
f ( x0 )
17.
§ 3. Правила дифференцированияфункций. Таблица производных
Пусть u = u (x) и v = v (x) – дифференцируемые функции
независимой переменной x, c = const.
Тогда
1) с′ = 0, x′ = 1;
2) (правило дифференцирования алгебраической суммы
функций) (u ± v)′ = u′ ± v′.
u x x v x x u x v x
Доказательство. u x v x lim
x 0
x
u x x u x v x x v x
u x v x
lim
lim
x
0
x 0
x
x
u x
v x
lim
lim
u x v x . Доказано.
◄
x 0 x
x 0 x
3) (правило дифференцирования произведения функций)
(uv)′ = u′v + uv′;
4) (cu)′ = cu′ ;
Упражнение. Доказать правила 3, 4.
18.
5) (правило дифференцирования частного функций)u u v v u (v ≠ 0);
v2
v
Доказательство.
u u ( x x) u ( x) u ( x x)v( x) u ( x)v( x x)
v x x v x
v v( x x ) v x
u u ( x x) u x u( x x) u u x (аналогично для v = v (x))
u u x v( x) u ( x) v v x u v x u x v
,
v x x v x
v x x v x
u
v
v x u x lim
u x
u v x u x v lim
x 0 x
x 0 x
lim
x 0
x v x x v x
v x x v x
v x
u v u v
v2
Доказано.
◄
19.
6) производная сложной функции. Рассмотрим сложнуюфункцию y(x) = f (u(x)), где y = f (u), u = u(x).
Теорема о дифференцируемости сложной функцииПусть функция
u = u(x) дифференцируема в точке x0, а функция y = f (u)
дифференцируема в точке u0 = u(x0). Тогда сложная функция
y(x) = f (u(x)) дифференцируема в точке x0 и ее производная имеет
вид
y x x0 fu u0 u x x0 или символически
y x fu u x или
dy dy du
;
dx du dx
Доказательство.
Из дифференцируемости функций u = u(x) и y = y(u) следует их
непрерывность, тогда при x → 0 следует u → 0.
y
u u u x , y y u
y
y u
lim
lim
lim
yu u x .◄
u
0
x
0
x 0 u x
x 0 x
u
x дифференцируемы
y lim
Доказано.
Цепочное правило дифференцирования сложной функции: для
случая нескольких промежуточных аргументов:
dy
y (t ) f ( g (q(u ( x(t )))))
f g g q qu u x xt .
dt
20.
7) Теорема о дифференцируемости обратной функции. Пустьфункция y = f (x) непрерывна, строго монотонна на интервале
(a; b) и в точке x0 (a; b) имеет конечную и неравную нулю
производную f ′ (x0) ≠ 0. Тогда для обратной функции x = f –1(y) в
соответствующей точке y0 = f (x0) также существует производная,
1
1
1
равная x
, y , если
или кратко x
y
f x x
y
y x
x
x y
y x 0, x y 0.
Доказательство.
Рассмотрим функцию x = x(y). Зададим приращение y ≠ 0. В
силу строгой монотонности функции y = y(x) этому приращению
соответствует приращение x ≠ 0. Т. к. функция y = y(x)
непрерывна в точке y0 = y(x0), то y 0 x 0.
1
x
1
.Доказано.
y 0 y
y y
x ( x0 ) y ( x )
x
0
lim
x 0 x
x y ( y0 ) lim
◄
21.
Пример 1.y ln x x e ,
y
1
1 1
1
y .
y x ln x
e
x
x y
y
e
22.
Таблица производныхПусть u = u(x), где х независимая переменная.
1). (u )′ = u –1u′, α R;
8). tg u
1а). (x)′ = 1;
1б).
x 2 x ;
1
1
1в). 12 ;
x
x
2). (au)′ = au lna u′ (a > 0, a ≠ 1);
3). (eu)′ = eu u′;
1
u ;
2
cos u
9). ctg u
1
u ;
2
sin u
10). arcsin u
1
1 u2
11). arccos u
1
u ;
4). log a u
u ln a
1
5). ln u u ;
u
12). arctg u
6). (sin u)′ = cos u u′;
13). arcctg u
7). (cos u)′ = –sin u u′;
u ;
1
1 u
2
u ;
1
u ;
2
1 u
1
u .
2
1 u
23.
Доказательство.alogab = b.
1
ln xα
1. x e
e α ln x e α ln x (α ln x) x α α α xα-1.
x
x
x ln a
2. a x e x ln a e ( x ln a) a ln a.
1
ln x
4. log a x
x ln a .
ln a
y sin x x sin x
6. у = sin x.
α
x x x
x x x
x
x
2sin
cos
2sin
cos
x
.
2
2
2
2
x
x
x
x
sin cos x
2sin cos x
y
2
2
2
2
lim
y lim
lim
x
x 0
x 0
x 0 x
x
2
x
1
lim cos x
cos
x
.
x 0
2
π
π
y
cos
x
sin
x
,
7.
x u,
2
2
π
y sin u cosu u cos x 1 sin x.
2
24.
8. 9. y = tg x и y = ctg xsin x cos x cos x sin x sin 2 x cos 2 x
sin
x
1
tg x
.
2
2
2
cos x
cos x
cos x
cos x
10. y = arcsin x. x = sin y.
1
1
1
1
y x
.
; cos y 0.
2
2
x y cos y
2 2
1 sin y
1 x
Упражнение. Доказать формулы 9, 11, 12, 13.
Пример 2. Найти производные функций:
)′ = u –1u′
1
5
(u
x arctg x;
а) y x
(uv)′ = u′v + uv′
x
1
5 1
y x
x arctg x x5 x 2 xarctgx 5x 4
x
1
1 2 1
x
x arctg x x arctg x 5 x 4 1 3 arctg x x ;
2
2
1
x
2
2
x
1
u ;
arctg u
2
1 u
25.
u u v v uu)′ = eu u′;
;
(e
(sin u)′ = cos u u′;
2
v
v
x
e
;
sin x
e x
e x sinx e x sinx e xsinx e xcosx e x sinx cosx
y
;
2
2
2
sin
x
sin x
sin x
sin x
б) y
(sin u)′ = cos u u′;
в) y sin 2 x x ; (u )′ = u –1u′
3 5
3 4
y ' sin 2 x x
5 sin 2 x x sin 2 x x3
3 5
5 sin 2 x x 2cos 2 x 3x 2 ;
3 4
г) y ln 3 tg 5 x.
ln u u ;
u
3
3 1
3
y ln tg 5 x ln tg 5x 3 ln tg 5 x ln tg 5 x
1
1
1
2
2
5x
3ln tg 5 x
tg 5 x 3ln tg 5 x
2
tg 5 x cos 5 x
tg 5 x
1
1
tg u
cos 2 u
u;
2
2
1
1
15ln
tg5
x
30ln
tg 5 x
3ln 2 tg 5 x
5
.
2
tg 5 x cos 5 x
cos5 x sin 5 x
sin10 x
26.
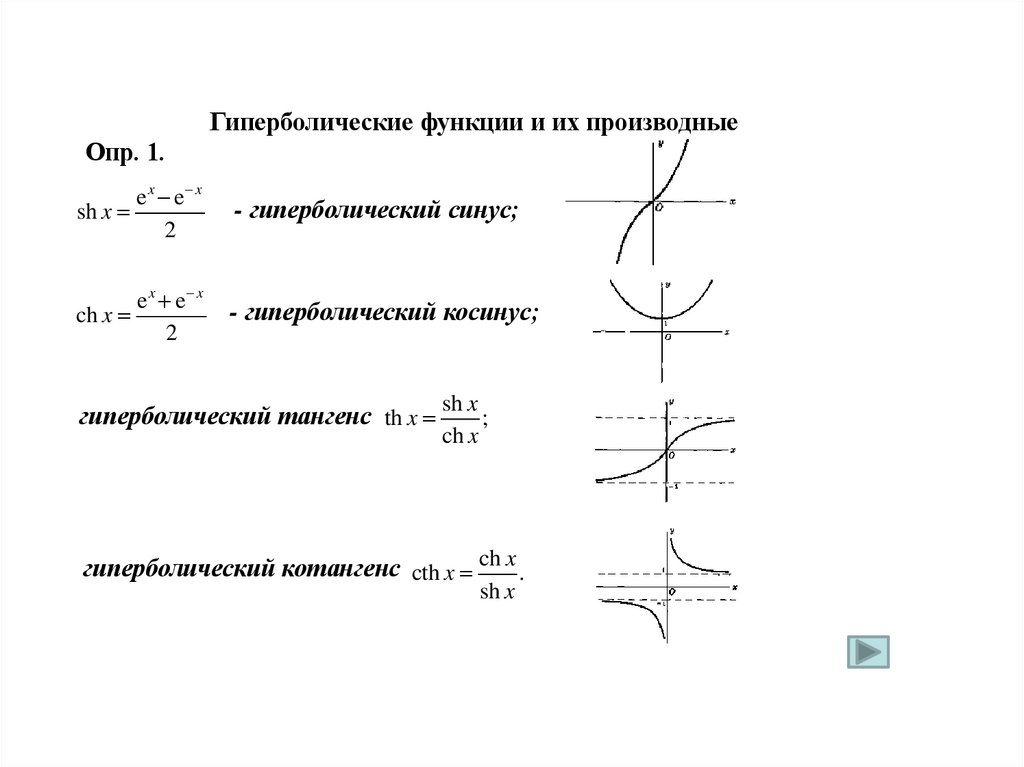
Гиперболические функции и их производныеОпр. 1.
e x e x
sh x
2
- гиперболический синус;
e x e x
ch x
2
- гиперболический косинус;
гиперболический тангенс th x
sh x
;
ch x
гиперболический котангенс cth x ch x .
sh x
27.
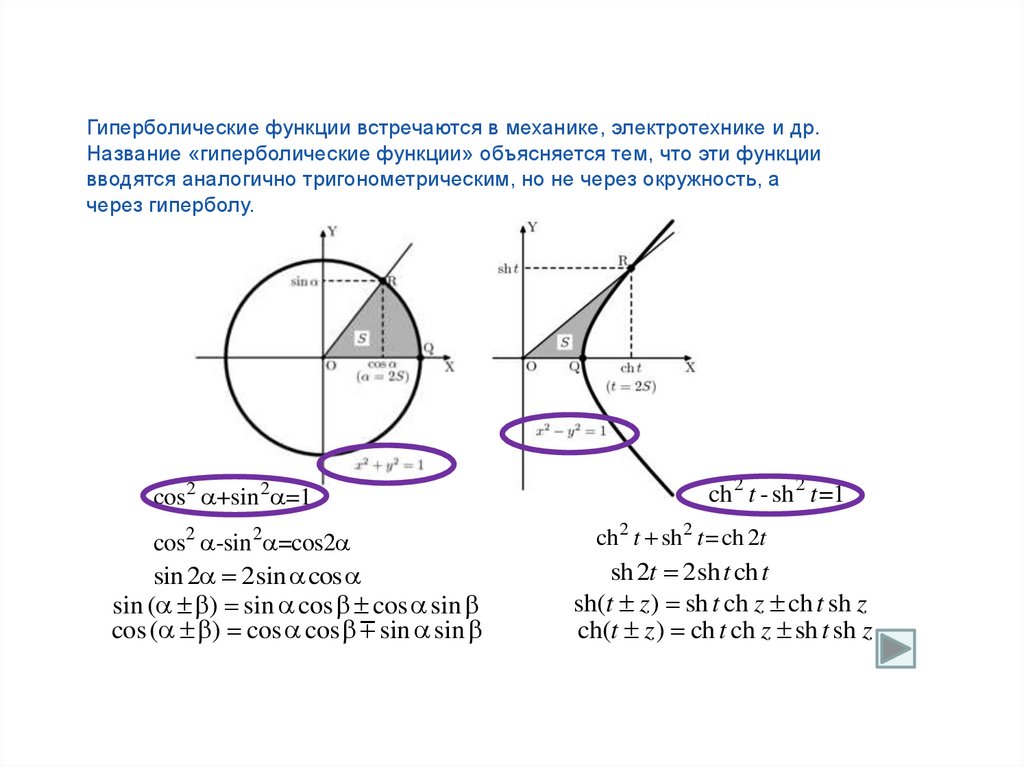
Гиперболические функции встречаются в механике, электротехнике и др.Название «гиперболические функции» объясняется тем, что эти функции
вводятся аналогично тригонометрическим, но не через окружность, а
через гиперболу.
cos2 +sin 2 =1
cos2 -sin 2 =cos2
sin 2 2sin cos
sin ( ) sin cos cos sin
cos ( ) cos cos sin sin
ch 2 t - sh 2 t =1
ch 2 t sh 2 t = ch 2t
sh 2t 2sh t ch t
sh(t z ) sh t ch z ch t sh z
ch(t z ) ch t ch z sh t sh z
28.
График гиперболическогокосинуса называют также цепной
линией, так как именно такую
линию образует тяжелая
нерастяжимая нить (цепь) при
свободном провисании.
Перевёрнутая цепная линия —
идеальная с точки зрения прочности
форма для арок.
Арка «Врата на запад» в
Сент-Луисе, США,
На арке написана
формула в футах:
архитектор
Ээро её
Сааринен
y 127, 7 ch
x
757, 7
127, 7
29.
Упражнение . Показать, чтоsh x ch x;
th x
1
;
2
ch x
1
ch
x
sh
x
;
cth
x
.
2
sh x
30.
д)x2 4 x
3
5
1
y
;
3
x 1 ( x 2) 2 2
dy
?
dx
x2 4 x
dy
3
5
1
y'
2
2
dx
3
x
1
(
x
2)
(c)′ =
(u )′ = u –1u′
0
1 2
1
2
x 4 x 3 ( x 1) 5 ( x 2) 0
3
1
1
3
10
2 x 4 3 ( 1)( x 1) 2 5 ( 2)( x 2) 3 2 x 4
.
2
3
3
3
( x 1) ( x 2)
3
x
2
x
1
dy
е).
y
3x 2 3 x
4 e;
?
5
6
4
3
dx
(c)′ =
x
x
1
73 56 0
dy
1 12
12 1 3
y ' x 2 x x 3 x x 0
dx
4
3
4
1
2
3
–1
(u )′ = u u′
1 1 2
7 3 5 116
1 2 1 1 3
x 2 x x 3 x x
4 2
3 3
3
6
2
1
8 x
1
x x
1
3
9 x
2
7x 3 x
5
6
6x x
5
.
31.
§ 4. Логарифмическоедифференцирование
Этот метод используется при дифференцировании степеннопоказательных функций y u ( x)v ( x ) , и функций вида
f1 ( x) f 2 ( x) f m ( x)
Суть метода: ln y = ln f (x),
y
.
g1 ( x) g 2 ( x) g n ( x)
y
y
(ln f ( x)) .
y y (ln f ( x)) f ( x) (ln f ( x)) .
Здесь надо учитывать, что x – независимая переменная и x′ = 1,
а y = y(x) – зависимая переменная и (y(x))′ = y′.
Пример 1. Найти производную функции y = (tg x)sin x.
sin x
ln y ln tg x sin x ln tg x;
ln y sin x ln tg x ;
y
1
sinx ln tg x sinx ln tg x cosx ln tg x sinx
;
2
y
tg xcos x
1
ln u u ; (uv)′ = u′v + uv′;
1
sinx
u
y tg x cosxln tg x
1
.
u ;
(sin u)′ = cos u u′; tg u
cosx
cos u
2
32.
x2 x 1 3 2 x 1Пример 2. y
, x 0.
5
x 3
x2 x 1 3 2 x 1
2
3
5
ln y ln
ln
x
ln
x
1
ln
2
x
1
ln
x 3
5
x 3
1
1
1
2ln x ln x 1 ln 2 x 1 ln x 3 ;
2
3
5
1
1
1
lny 2lnx ln x 1 ln 2 x 1 ln x 3 ;
2
3
5
y 2
1
2
1
,
y x 2( x 1) 3(2 x 1) 5( x 3)
1
ln
u
u ;
u
x2 x 1 3 2x 1 2
1
2
1
.
y
5
x 3
x 2( x 1) 3(2 x 1) 5( x 3)
33.
§ 5. Производные функций, заданныхнеявно и параметрически
Пусть функция y = y(x) задана неявно, т. е. соотношением вида
F(x; y) = 0.
F x, y x 0 x a; b .
Для нахождения y x следует продифференцировать обе части
последнего тождества, учитывая, что x – независимая
переменная и x′ = 1, а y = y(x) – зависимая переменная,
(y(x))′ = y′. Затем выражают y x .
Пример 1. Найти производную неявно заданной функции
y2x + exy = 0.
( y 2 x e xy ) (0) ;
y ( y e xy )
( y 2 ) x y 2 x e xy ( xy) 0;
y
.
xy
2 xy xe
2 y y x y 2 1 e xy 1 y xy 0;
2 y y x xy e xy ( y 2 ye xy );
34.
Пусть y = y(x) – функция, заданная параметрическиx x t ,
, t (t0 ; t1 ),
y y t
где x(t) и y(t) дифференцируемые функции, x′(t) ≠ 0.
Кроме этого, будем считать, что функция x = x(t) имеет
обратную функцию t = φ–1(x), которая также дифференцируема.
Тогда функцию y = y(x) можно рассматривать как сложную
функцию y = y(t), t = φ–1(x), считая t промежуточным аргументом.
yt
y x .
xt
y
y
lim
yt
y
t 0 t
t
.
y x lim
lim
x xt
x 0 x
x 0 x
lim
t 0
t t 0 t
Функция x = x(t) дифференцируема, а следовательно, и
непрерывна. Поэтому ∆t → 0 при ∆x → 0.
◄
35.
Пример 2. Найти y x ,если
y 1 cos t ,
x t sin t.
yt sin t ,
xt 1 cos t ,
t
t
2sin cos
t
sin t
2
2
y x
ctg .
2
2 t
1 cos t
2sin
2
36.
§ 6. Производные высших порядковПусть функция y = f (x) дифференцируема в точке х. Если ее
производная y′ = f ′(x) (производная 1-го порядка) также
дифференцируема в точке x, то ее производная (f ′(x))′
называется производной 2-го порядка (второй производной)
2
d
исходной функции и обозначается f ″(x), y .
dx 2
Если же существует производная производной 2-го порядка,
то она называется производной
3-го порядка исходной функции
3
и обозначается y‴(x), f ‴(x), d y и т. д.
dx3
Производной n-го порядка называется производной от
n
n
(n)
(n–1)
d
y
d
f ( x)
производной (n – 1)-го порядка: f (x) = (f
(x))′.
dx
n
,
dx
n
Механический (физический) смысл второй производной от
функции пути по времени состоит в том, что она равна
ускорению прямолинейного движения точки.
.
37.
Функция, имеющая n-ю производную в точке x0, называется nраз дифференцируемой в этой точке. Функция, имеющая в
точке x0 производные всех порядков, называется бесконечно
дифференцируемой в этой точке.
Основные правила вычисления n-ых производных.
Формула Лейбница
uv
n
n
C u
k 0
k
n
k
v
n k
, где
v
0
n!
v C
k ! n k !
k
n
38.
Пример 1.а) найти производную 2-го порядка от функции y = x3e2x;
2
3
2x
3 2x
2 2x
3 2x
3 2x
3
2x
3
x
2
x
e
;
y x e
x e x e
3x e 2 x e
2
3
2x
y 3x 2 x e
3x 2 2 x3 e2 x 3x 2 2 x3 e 2 x
6 x 6 x e 3 x 2 x 2e 2 x 3 6 x 2 x e ;
2
2x
2
3
2x
2
2x
б) найти производную 3-го порядка от функции y = cos2x.
y cos 2 x 2cos x sin x sin 2x;
y sin 2 x 2cos2 x;
y 2cos 2 x 4sin 2 x.
39.
Пример 2. Найти производные n-го порядка:x
1) y e y e x y e x y ( n) e x, n 1,2,...;
y
sin
x
y cos x sin x y sin x sin x
2)
2
3
IV
y cos x sin x
y
sin x sin x 2
2
n
y ( n ) (sin x)( n ) sin x
, n 0,1,2,...;
2
1
y (1 x) 2 y 2(1 x) 3
3) y ln(1 x) y
1 x
y IV 6(1 x) 4
y ( n ) ( 1)n 1 (n 1)! (1 x) n , n 1,2,...
40.
x x(t ),Пусть функция y = y(x) задана параметрически:
t (t0 ; t1 ).
y y (t ),
x x(t ),
y x t
t (t0 ; t1 ).
y xx
.
y
y
(
t
),
x
x
xt
( n 1)
В общем случае для n-й производной имеем
y
x... x t
(n)
( n 1)
yx... x yx... x
, n 1,2,...
x
xt
x a cos3 t ,
Пример 3. Найти производные y x и y xx функции
a const.
3
Решение.
y a sin t ,
xt a cos3 t 3a cos 2 t cos t 3a cos2 t sin t;
yt a sin 3 t 3a sin 2 t cos t.
sin t
3a sin 2 t cos t
y x
tg t.
2
cos t
3a cos t sin t
1
2
1
cos
t
y xx
.
2
4
3a cos t sin t 3a cos t sin t
y x t tg t
1
;
2
cos t
41.
Пусть функция y = y(x) задана неявно в виде уравнения F(x; y) = 0.Пример 4. Найти вторую производную функции 4х2 – у2 = 4.
Решение.
(4х2)′– (у2)′ = (4)′;
x
8x
y x
4 ;
y
2y
y xy
x
x y xy
4
y xx 4 4
2
2
y
y
y
x
4x2
y x 4
y
2
2
y
y
4
x
y
4
2
2
y xx 4
4
y
4
x
4
2
3
2
y
y
y
16
3.
y
8x 2 yy x 0
42.
Итак, для того, чтобы вычислить n-ю производную от какойлибо функции, нужно предварительно вычислить производныевсех предшествующих порядков.
Если y— неявная функция, то для отыскания ее высшей
производной
нужно
соответствующее
число
раз
дифференцировать заданное уравнение, связывающее x и y,
помня всегда, что y и все ее производные суть функции
независимой переменной.
Для того чтобы найти производную высшего порядка от
параметрически
заданной
функции,
нужно
продифференцировать
выражение
для
предыдущей
производной, как сложную функцию независимой переменной.
43.
§ 7. Дифференциал функцииЕсли функция y = f (x) дифференцируема в точке x0, то ее
приращение ∆y = f (x0 + ∆x) – f (x0) в этой точке представимо в
виде:
∆y = f ′(x0) ∆x + o(∆x),
при ∆x → 0,
где o(∆x) – бмф более высокого порядка малости, чем ∆x при
∆x → 0.
Опр.1. Главная (остаток ∆x) линейная (так как ∆x входит в
первой степени) часть приращения функции называется
дифференциалом функции в данной точке x0 соответствующая
приращению ∆x аргумента и обозначается df (x) или dy.
Необходимым и достаточным условием существования
дифференциала функции y = f (x) служит существование
производной, и тогда dy(x0) = f ′(x0) ∆x.
44.
Приращение Δx независимой переменной x называют еедифференциалом dx, т.е. Δx=dx.
Т.к. дифференциал функции y=x равен
dy=dx = x′ ∆x = 1∙∆x = ∆x, т.е. dx =Δx
Таким образом, дифференциал функции y = f (x) в точке x0
имеет вид dy = df (x)= f ′(x)dx = y′dx.
dy = y′dx.
Действия отыскания производной и дифференциала данной
функции носят общее название дифференцирование.
45.
Пример 1. Найти дифференциал функции y 5tgx x .Решение.
tg x
tg x
tg x
dy 5 x dx 5
x 5
x dx
tg x
1
x
5
tg x
tg x
tg x
5 ln5 tg x x 5
dx 5 ln 5 2
dx
2 x
cos x 2 x
2
tg x 2 x ln 5 cos x
5
dx.
2
2 x cos x
Пример 2. Найти приращение и дифференциал функции
y = 2x – x2 в точке x = 3 при ∆x = 0,1.
Решение.
∆y = y(3,1) – y(3); y(3,1) = 6,2 – 9,61 = –3,41, y(3) = 6 – 9 = –3,
∆y = –3,41 – (–3) = –0,41;
dy = (2x – x2)′dx = (2 – 2x)dx
dy = (2 – 6)0,1 = –0,4.
в точке x = 3 при ∆x = 0,1 имеем
46.
Правила для отыскания дифференциаловПусть u(x), v(x) – две дифференцированные функции, c –
const, тогда справедливы свойства:
1. dc = 0, c – const;
2. d(cu) = c du, c – const;
3. d(u ± v) = du ± dv;
4. d(uv) = u dv + v du;
u vdu udv
;
5. d
2
v
v
Так как дифференциал получается из производной
умножением ее на дифференциал независимой переменной, то,
зная производные основных элементарных функций, можем
составить таблицу дифференциалов этих функций:
и т.д.
47.
Дифференциал сложной функции. Инвариантность формыпервого дифференциала.
dy = f ′(x)dx называется первым дифференциалом функции.
Пусть y = f (x) и x = u(t), т. е. y является сложной функцией
переменной t: y = f (u(t)).
dy ft dt.
ft fu ut .
dy fu u t ut dt f x x dx f x dx.
dx
Это свойство называется инвариантностью формы 1-го
дифференциала.
Но есть и различие: dx = x для независимой переменной, а
du ≠ u в общем случае зависимой переменной.
48.
Из равенства dy=f ‘(u)du следует:Значит, во всех случаях скорость изменения функции
относительно
своего
аргумента
равна
отношению
дифференциала функции к дифференциалу аргумента.
Физический смысл дифференциала.
Если t — время, а s(t)— координата точки на прямой в момент
t, то дифференциал ds=s’(t)dt
равен тому изменению
координаты, которое получила бы точка за время Δt, если бы
скорость точки на отрезке времени [t;t+Δt] была постоянной и
равной s’(t).
Изменение скорости на этом отрезке приводит к тому, что
Δs≠ds.
Однако на малых промежутках времени Δt изменение
скорости незначительно и Δs≈ds=s’(t) Δt.
49.
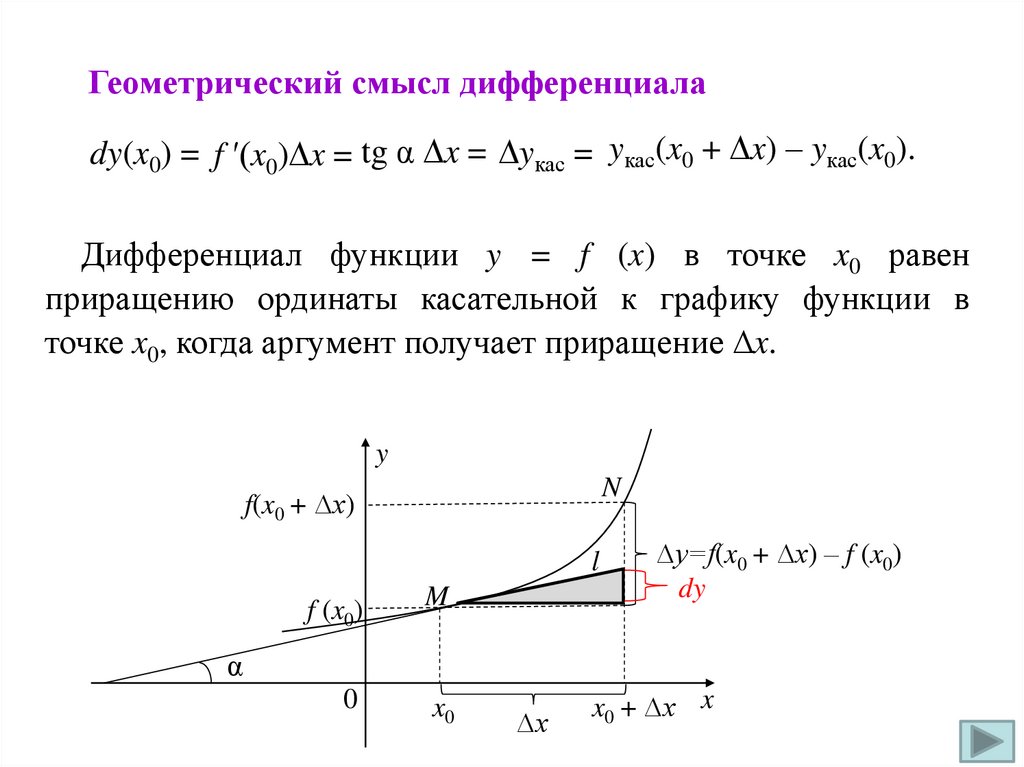
Геометрический смысл дифференциалаdy(x0) = f ′(x0) x = tg α x = yкас = yкас(x0 + x) – yкас(x0).
Дифференциал функции y = f (x) в точке x0 равен
приращению ординаты касательной к графику функции в
точке x0, когда аргумент получает приращение ∆x.
y
N
f(x0 + ∆x)
l
f (x0)
M
0
x0
∆y=f(x0 + ∆x) – f (x0)
dy
α
∆x
x0 + ∆x x
50.
Дифференциал функции y = f (x) в точке x изображаетсяприращением ординаты точки касательной, проведенной к
линии y = f (x) в соответствующей ее точке (x, f (x)).
Приращение же функции Δf изображается приращением
ординаты точки линии.
Поэтому разность между дифференциалом и приращением
изображается отрезком, заключенным между линией и
касательной к ней; этот отрезок является при ∆x → 0
бесконечно малой более высокого порядка, чем ∆x.
51.
∆y ≈ dy при малых x; ∆y = f (x0 + ∆x) – f (x0) ≈ dy = f ′(x0) x,Получим формулу для приближенных вычислений:
f (x0 + ∆x) ≈ f (x0) + f ′(x0) x,
где погрешность o(∆x) есть б. м. ф. более высокого порядка
малости, чем ∆x при ∆x → 0.
Полагая x = x – x0, получаем
f (x) ≈ f (x0) + f ′(x0)(x – x0),
что означает замену в окрестности точки x0 функции y = f (x)
линейной функцией y = kx + b, где k = f ′(x0), b = f (x0) – f ′(x0) x0,
т. е. линеаризацию функции в окрестности точки x0.
Пример 3. Вычислить приближенно
3,99.
y x , x0 = 4, x = –0,01.
1
f x0 4 2, f x 1
0,25,
0
2 x x 4 4
3,99 f 4 f 4 x 2 0,25 0,01 1,9975
52.
§ 8. Дифференциалы высших порядковПусть функция y = f (x) дифференцируема на интервале (a; b).
Первый дифференциал функции – dy = f ′(x)dx.
Второй дифференциал, или дифференциал 2-го порядка, –
дифференциал от дифференциала 1-го порядка:
d2y = d(dy) = d(f ′(x)∆x) = ∆x∙d(f ′(x)) = f ″(x)(∆x)2.
Аналогично d3y = d(d2y) = f ‴(x)(∆x)3 – дифференциал 3-го
порядка и т. д.
Дифференциалом dny n-го порядка функции y = f (x)
называется дифференциал от дифференциала (n – 1)-го порядка:
dny = d(dn – 1y).
Найдем теперь выражения для дифференциалов высших
порядков от функции f(x), причем предположим, что ее аргумент
есть независимая переменная.
53.
В случае функции y = f (x) независимой переменной x имеемdny = f (n)(x) dxn,
где dxn = (dx)n = (∆x)n.
Итак,
дифференциал n-го порядка равен произведению
производной n-го порядка по независимой переменной на n-ю
степень дифференциала независимой переменной.
Дифференциалы
высших
порядков
(в
отличие
от
дифференциалов 1-го порядка) инвариантностью формы не
обладают.
Пусть y=f (x) и x=φ(t), так что y можно рассматривать как
сложную функцию от t: y=f(φ(t)).
54.
Ее (первый) дифференциал по t:есть функция от t.
Вычисляем второй дифференциал по t:
, где


















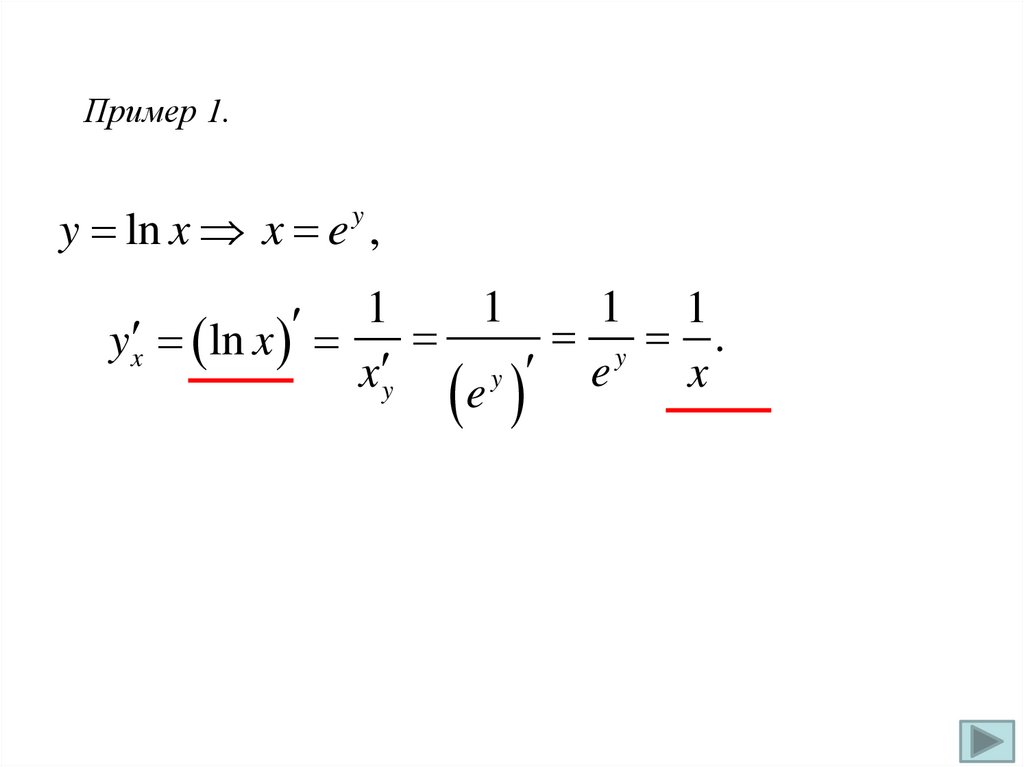



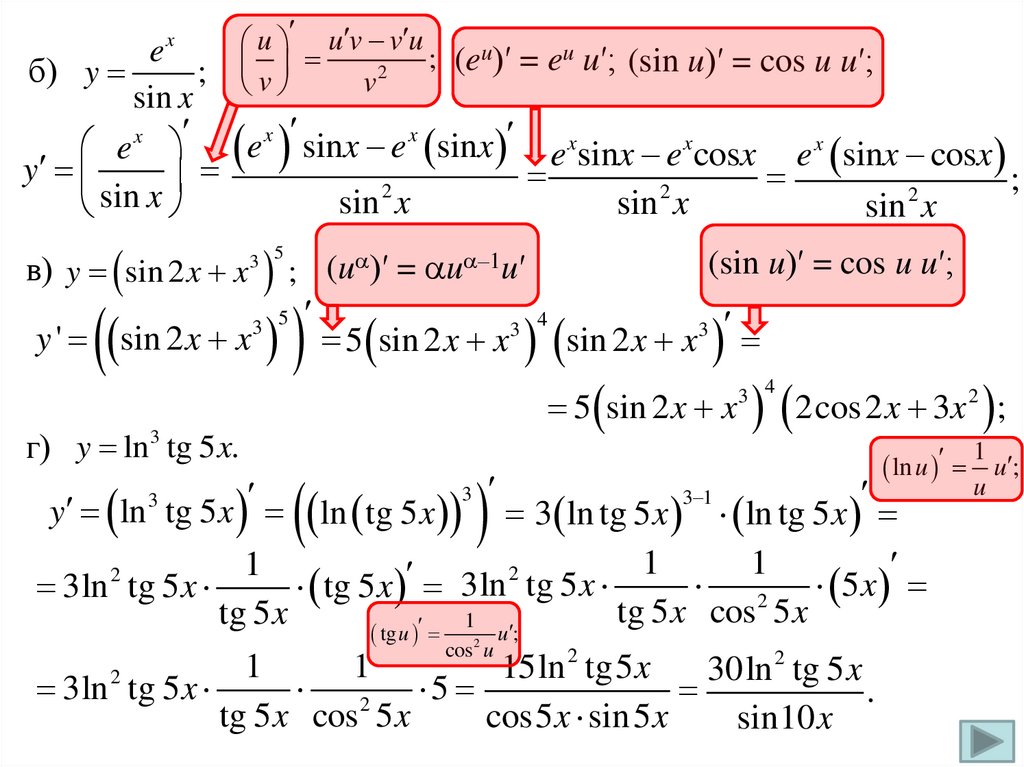




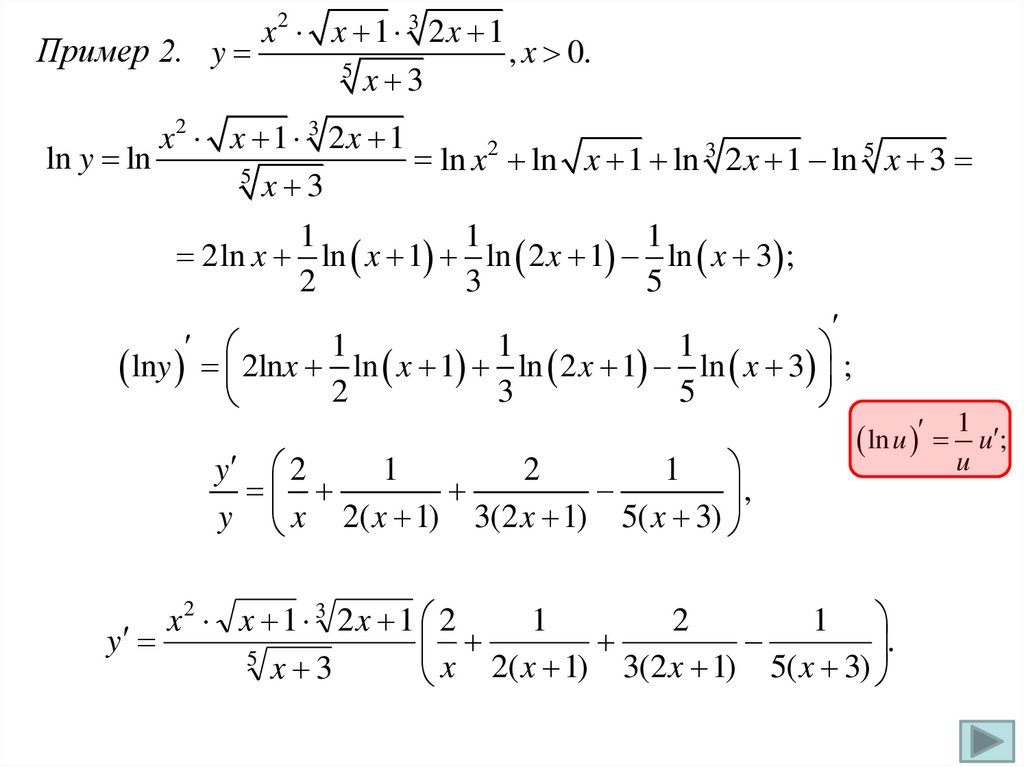


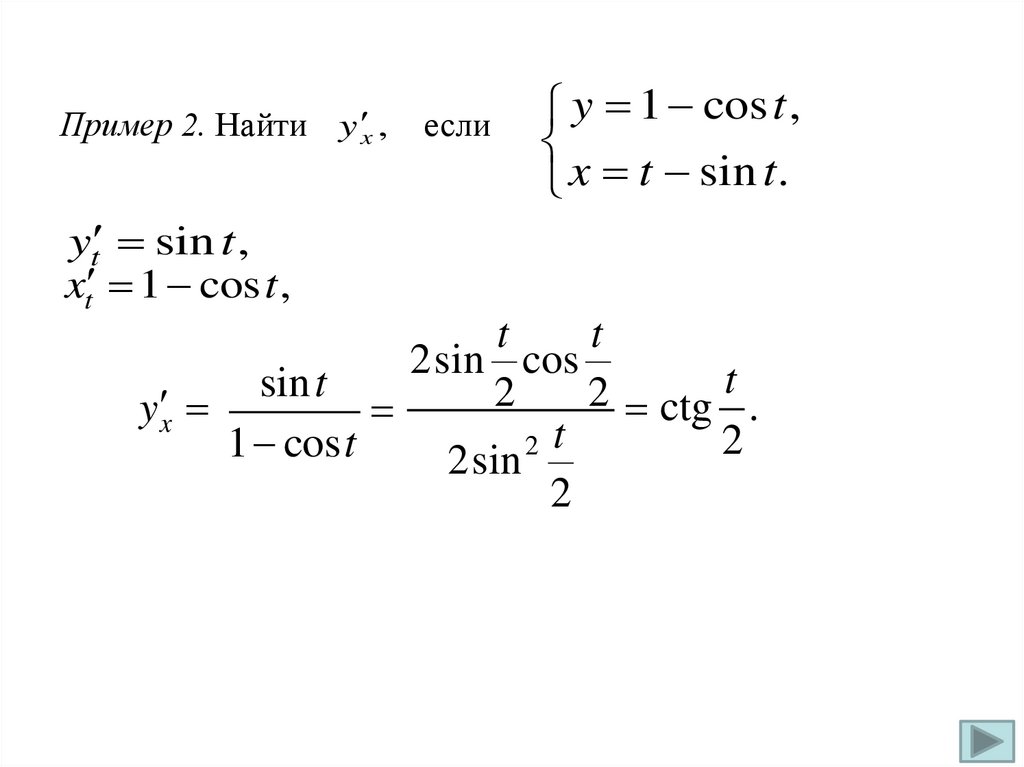


















 mathematics
mathematics








