3.4. Метод преобразования

1. ПОСТОЯННЫЙ ТОК   Методы исследования сложных цепей 1.6.4. Метод преобразования

ПОСТОЯННЫЙ ТОК
Методы исследования сложных
цепей
1.6.4. Метод преобразования

2.

Метод состоит в приведении путем преобразований сложной цепи в
простейшую.
Эти
преобразования
заключены
в
определении
эквивалентных сопротивлений при последовательном и параллельном
соединении.
Рассмотрим цепь, представленную на рис. 1.24.
r47
r45 r6 r1
r45 r6 r1
; rэ r1 r23 r47
Рис. 1.24. Пример преобразования сложной цепи в простейшую
(1.40)

3.

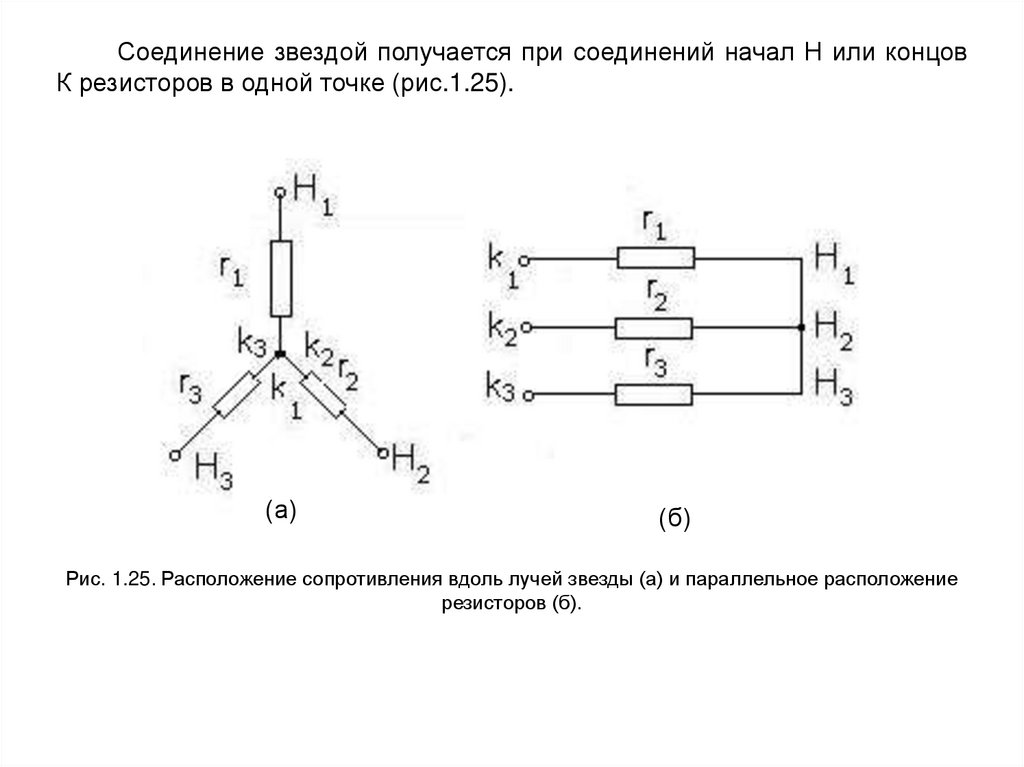
Соединение звездой получается при соединений начал Н или концов
К резисторов в одной точке (рис.1.25).
(а)
(б)
Рис. 1.25. Расположение сопротивления вдоль лучей звезды (а) и параллельное расположение
резисторов (б).

4.

Соединение многоугольников – если конец каждого сопротивления
соединить с началом последующего и конец последнего сопротивления – с
началом первого (рис. 1.26).
Часто необходимо для упрощения цепи преобразовать соединение
звездой в эквивалентное соединение треугольником или наоборот.
Пусть в сложную цепь входит группа резисторов r12, r23, r31,
соединенные треугольником и присоединенных к точкам 1, 2, 3 внешней
цепи (см. рис. 1.27, а).
Рис. 1.26. Соединение многоугольников.

5.

(а)
(б)
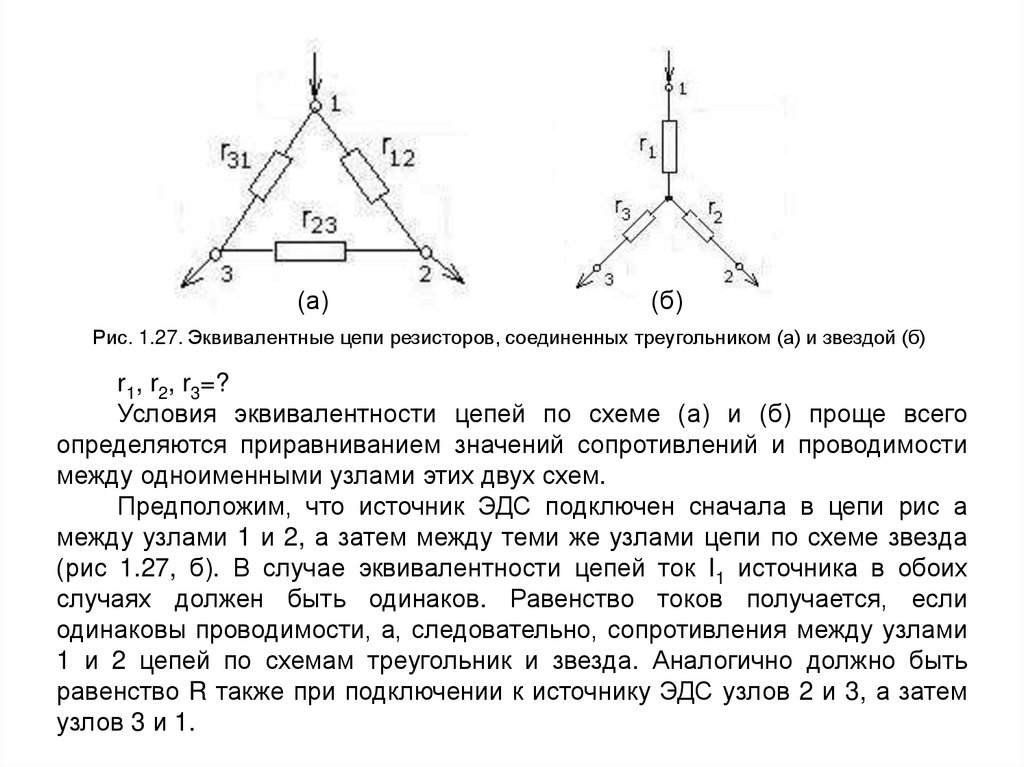
Рис. 1.27. Эквивалентные цепи резисторов, соединенных треугольником (а) и звездой (б)
r1, r2, r3=?
Условия эквивалентности цепей по схеме (а) и (б) проще всего
определяются приравниванием значений сопротивлений и проводимости
между одноименными узлами этих двух схем.
Предположим, что источник ЭДС подключен сначала в цепи рис а
между узлами 1 и 2, а затем между теми же узлами цепи по схеме звезда
(рис 1.27, б). В случае эквивалентности цепей ток I1 источника в обоих
случаях должен быть одинаков. Равенство токов получается, если
одинаковы проводимости, а, следовательно, сопротивления между узлами
1 и 2 цепей по схемам треугольник и звезда. Аналогично должно быть
равенство R также при подключении к источнику ЭДС узлов 2 и 3, а затем
узлов 3 и 1.

6.

Проводимость между точками 1 и 2 при соединении звездой является
обратной величиной суммы R между этими точками:
1
r1 r2
а проводимость при соединении треугольником
проводимостей параллельных ветвей 1–2 и 1–3–2
1
1
r12 r23 r31
(1.41)
равна
сумме
(1.42)
Приравняем эти проводимости
1
1
1
r1 r2 r12 r23 r31
(1.43)
Аналогично между точками 1 и 3:
для звезды
для треугольника
1
1
1
r1 r3 r31 r23 r12
Для точек 2 и 3:
для звезды
(1.44)
для треугольника
1
1
1
r3 r2 r32 r31 r12
(1.45)

7.

Из этих равенств находим
для звезды:
r12 r31 r12 r23
r3 r2
r12 r23 r31
r23 r12 r23 r31
r2 r3
r12 r23 r31
r r r r
r3 r1 31 12 31 23
r12 r23 r31
для треугольника:
r12 r31
r1
r12 r23 r31
r12 r23
r2
r12 r23 r31
r23 r31
r3
r12 r23 r31
(1.46)
(1.47)
(1.48)
(1.49)
(1.50)
(1.51)

8.

Решение этой же системы уравнений относительно сопротивлений r1,
r2, r3 определяет возможность замены в эквивалентной схеме звезды
сопротивлений r1, r2, r3 треугольной сопротивлениями r12, r23, r31,
следовательно
r1r2
r12 r1 r2
;
r3
(1.52)
r2 r3
r23 r2 r3
;
r1
(1.53)
r3 r1
r31 r3 r1
;
r2
(1.54)
Если при расчете цепи было произведено преобразование звезды в
эквивалентный треугольник и после расчета цепи определены токи,
текущие к узлам 1, 2 и 3 (I1, I2, I3) рис а, то эти токи и будут токами ветвей
звезды.
Для очень сложных цепей расчет невозможен.
Следующая тема