Similar presentations:
Преобразование графиков функций
1.
«Преобразованиеграфиков
функций»
2.
Задачи:Изучить преобразования графиков;
Применить преобразования графиков для
построения
графиков
кусочно-заданных
функций, функций, содержащих знак модуля;
Показать, что графиками можно рисовать
3.
ОПРЕДЕЛЕНИЕГрафиком
функции
называется
множество
точек
координатной
плоскости, у которых значения х и у
связаны некоторой зависимостью и
каждому значению х соответствует
единственное значение у .
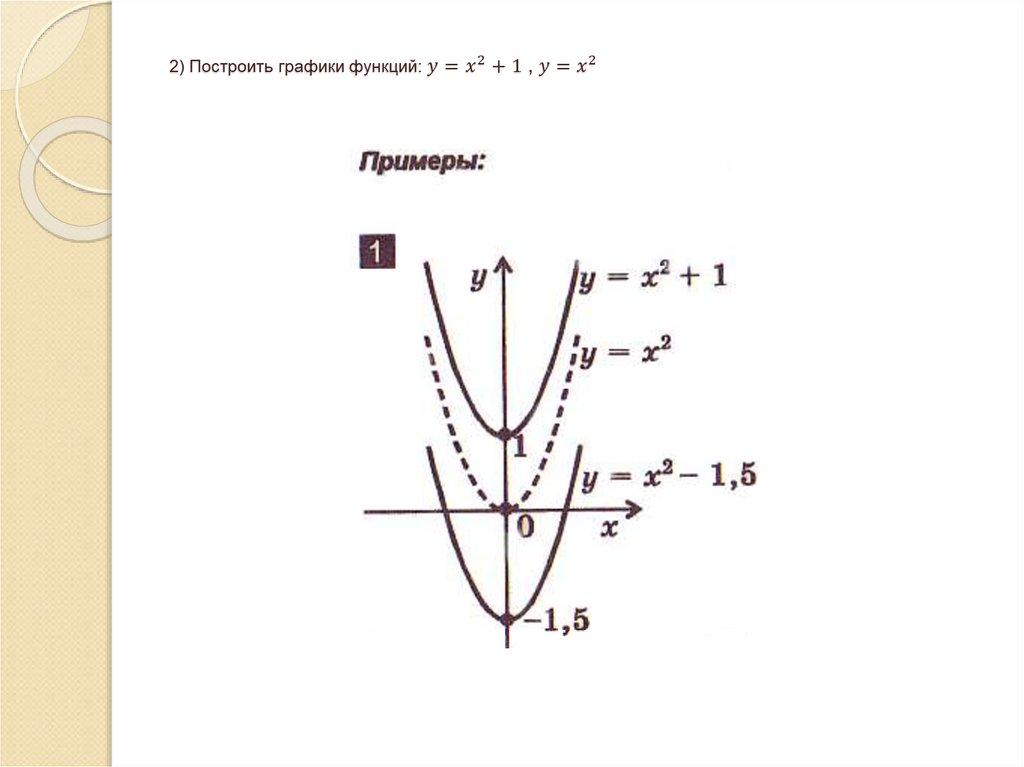
4. который получается из графика функции , путем смещения последнего вдоль оси ОУ:
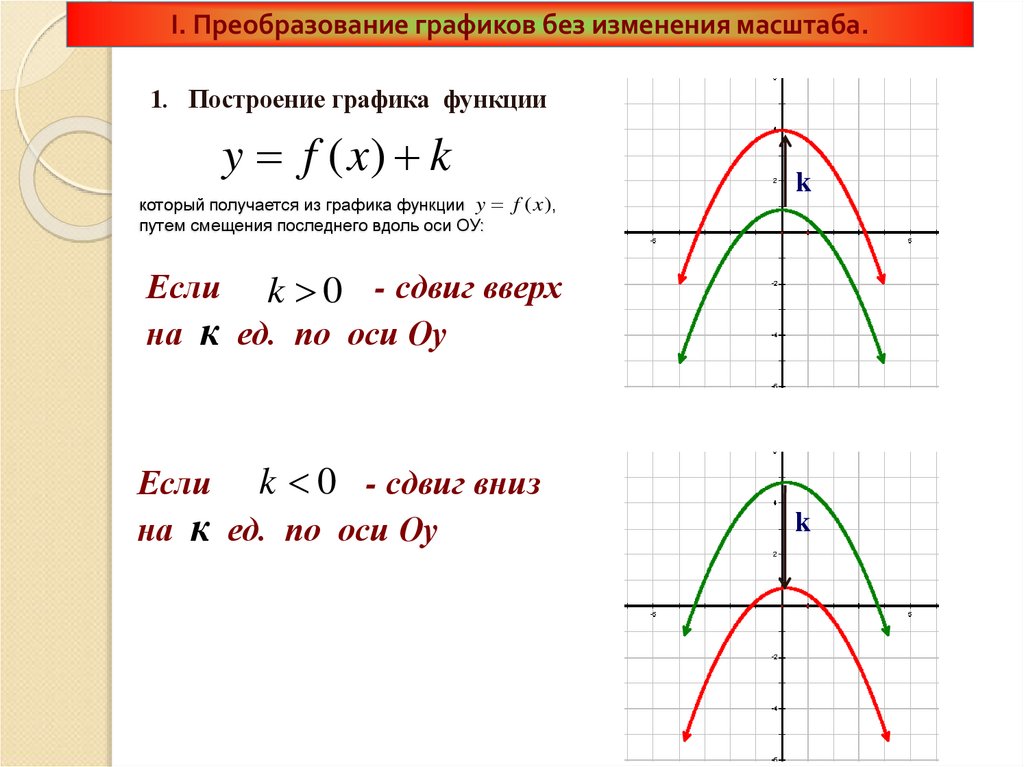
I. Преобразование графиков без изменения масштаба.1. Построение графика функции
y f ( x) k
который получается из графика функции y f (x),
путем смещения последнего вдоль оси ОУ:
k
Если k 0 - сдвиг вверх
на к ед. по оси Оу
Если k 0 - сдвиг вниз
на к ед. по оси Оу
k
5. который получается из графика функции , путем смещения последнего вдоль оси ОХ:
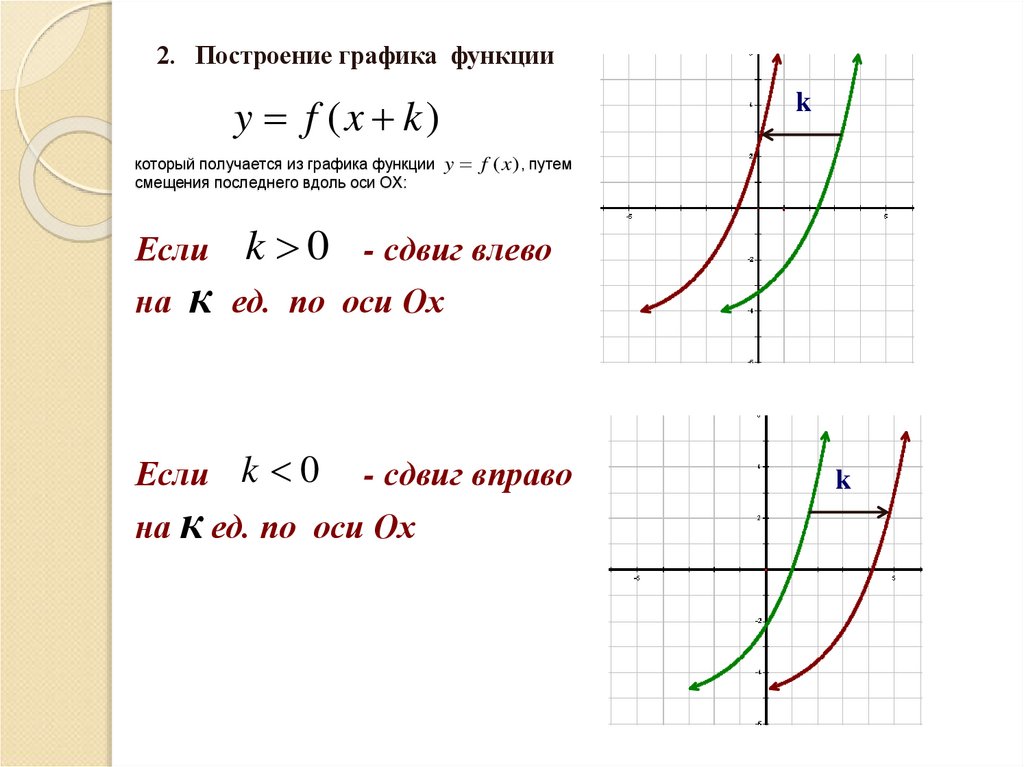
2. Построение графика функцииy f (x k)
k
который получается из графика функции y f (x) , путем
смещения последнего вдоль оси ОХ:
Если
k 0 - сдвиг влево
на к ед. по оси Ох
Если k 0
- сдвиг вправо
на к ед. по оси Ох
k
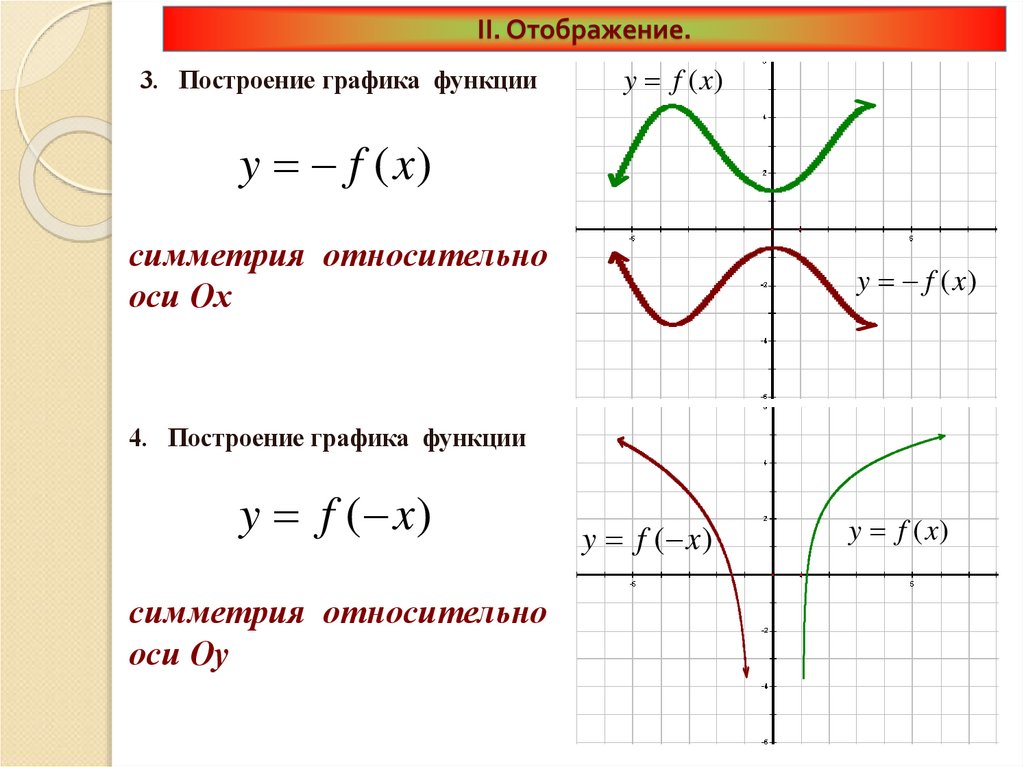
6. II. Отображение.
3. Построение графика функцииy f (x)
y f (x)
симметрия относительно
оси Ох
y f (x)
4. Построение графика функции
y f ( x)
симметрия относительно
оси Оу
y f ( x)
y f (x)
7.
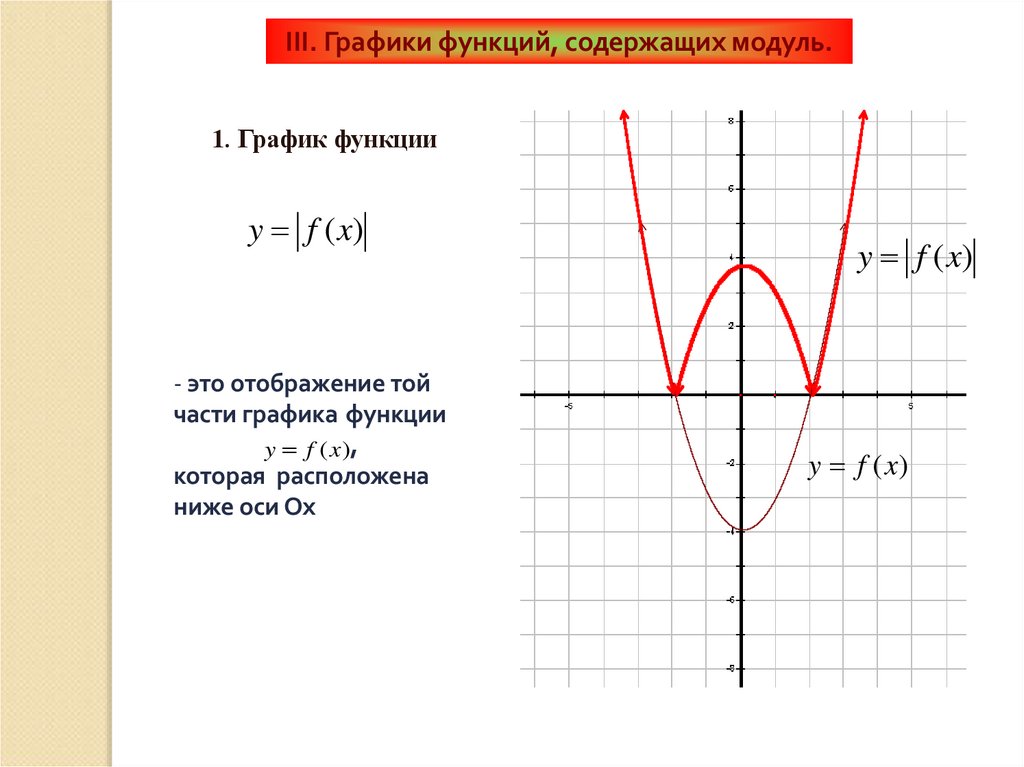
III. Графики функций, содержащих модуль.1. График функции
y f (x)
- это отображение той
части графика функции
y f (x),
которая расположена
ниже оси Ох
y f (x)
y f (x)
8.
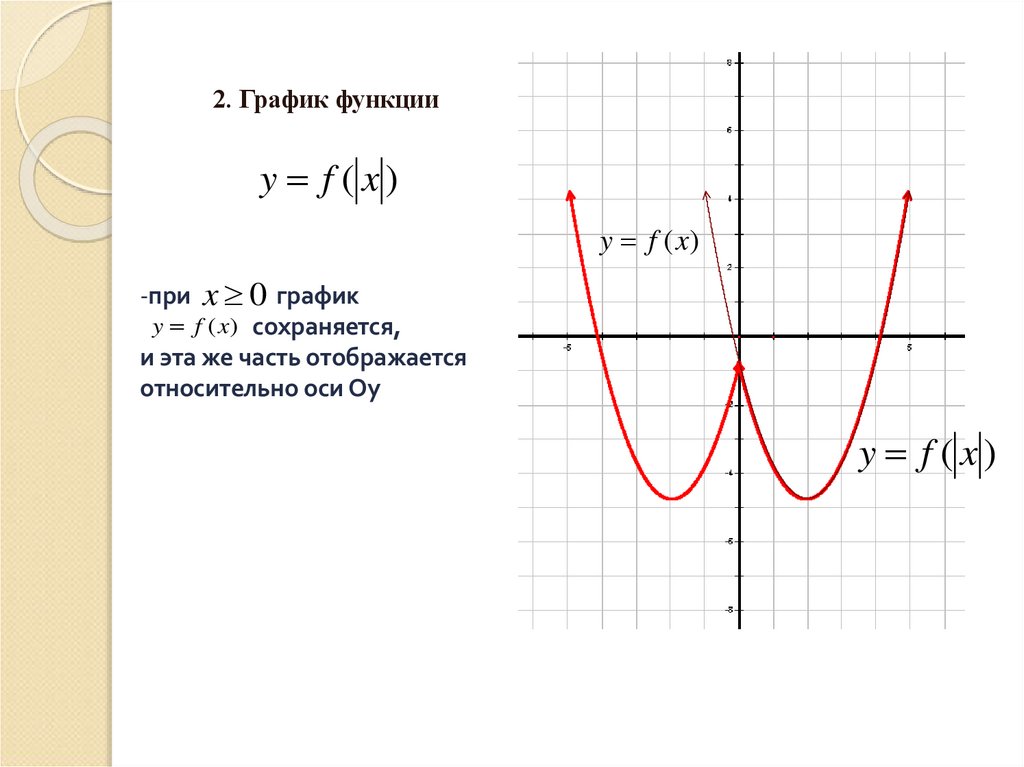
2. График функцииy f ( x)
y f (x)
-при x 0 график
y f (x) сохраняется,
и эта же часть отображается
относительно оси Оу
y f ( x)
9. IV. Преобразование графиков функций с изменением масштаба.
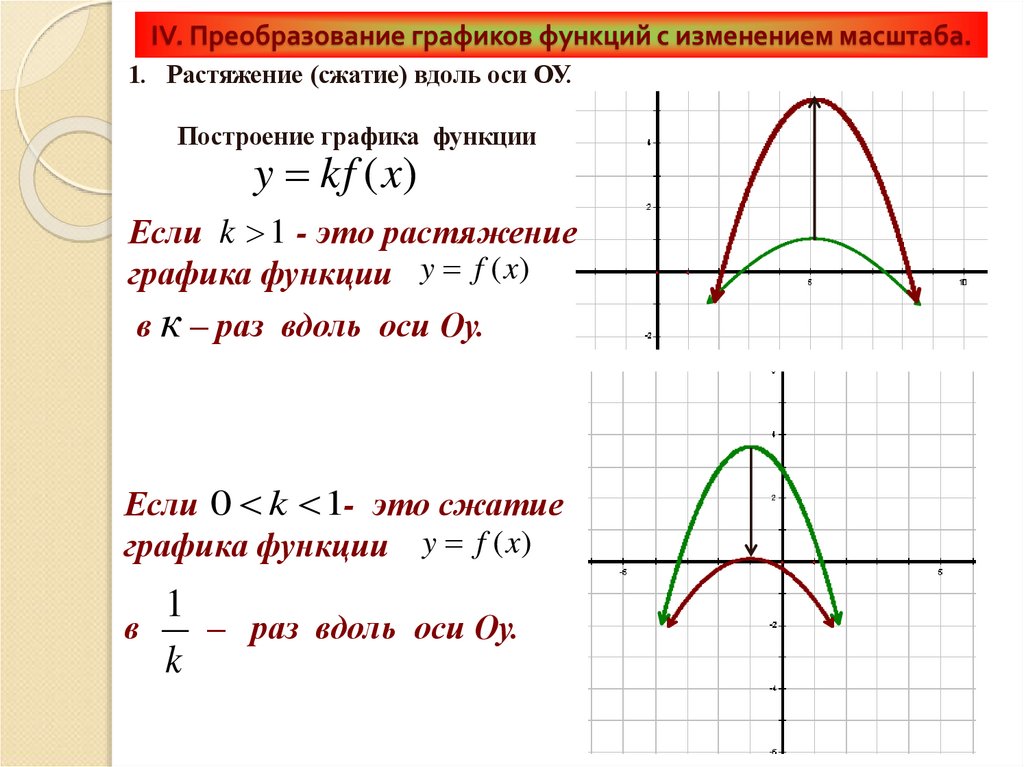
1. Растяжение (сжатие) вдоль оси ОУ.Построение графика функции
y kf (x)
Если k 1 - это растяжение
графика функции y f (x)
в к – раз вдоль оси Оу.
Если 0 k 1- это сжатие
графика функции y f (x)
1
в
– раз вдоль оси Оу.
k
10.
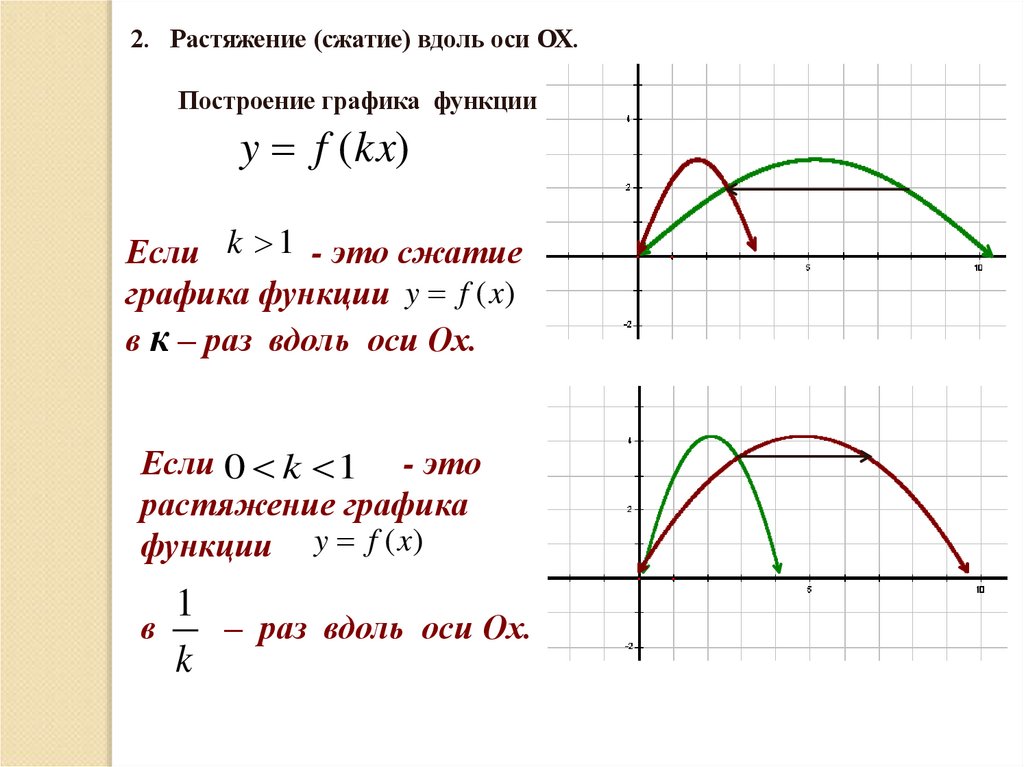
2. Растяжение (сжатие) вдоль оси ОХ.Построение графика функции
y f (kx)
Если k 1 - это сжатие
графика функции y f (x)
в к – раз вдоль оси Ох.
Если 0 k 1 - это
растяжение графика
функции y f (x)
1
в
– раз вдоль оси Ох.
k
11.
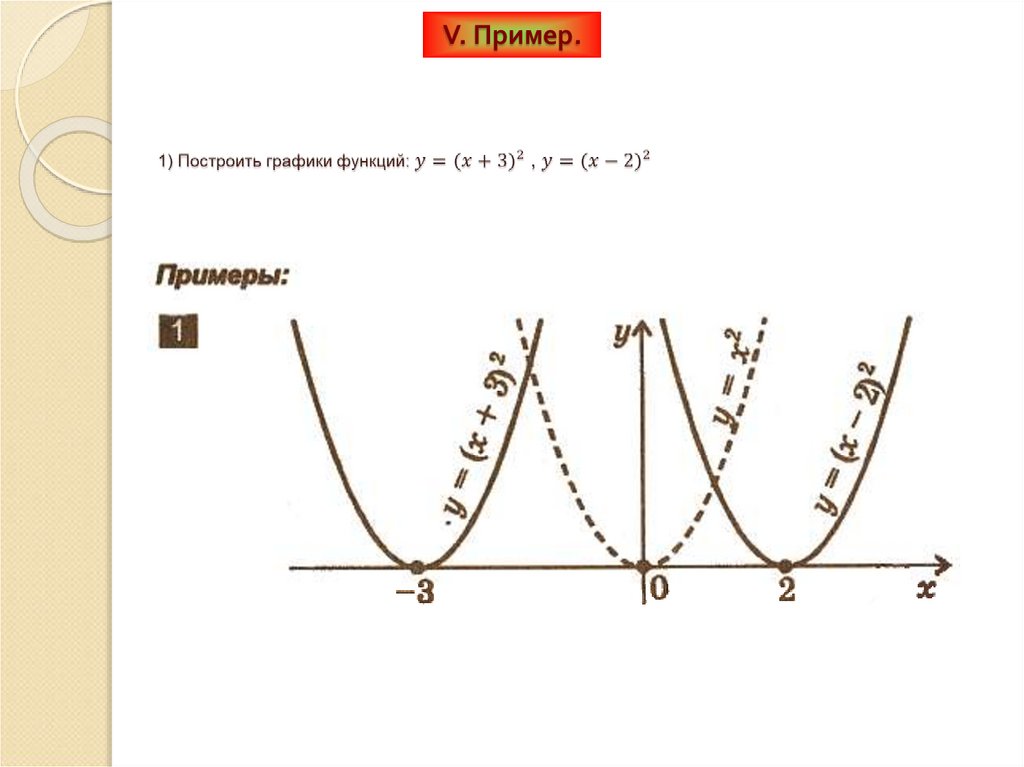
V. Пример.12.
13.
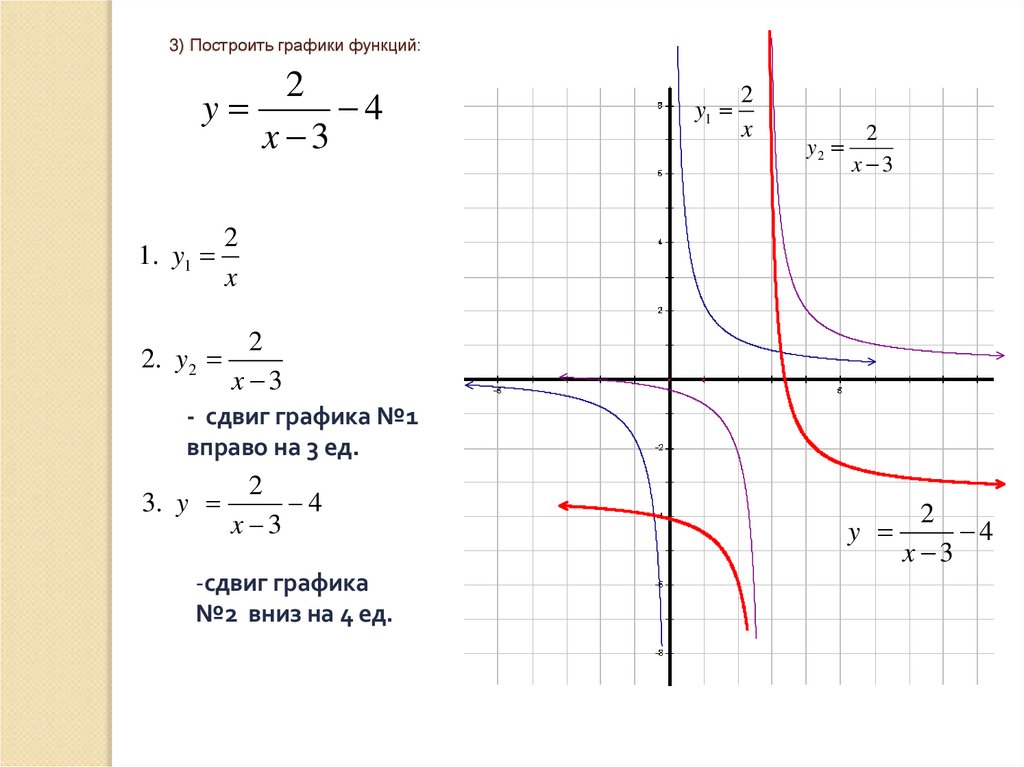
3) Построить графики функций:2
y
4
x 3
1. y1
2
x
2. y 2
2
x 3
y1
2
x
y2
2
x 3
- сдвиг графика №1
вправо на 3 ед.
3. y
2
4
x 3
-сдвиг графика
№2 вниз на 4 ед.
y
2
4
x 3
14.
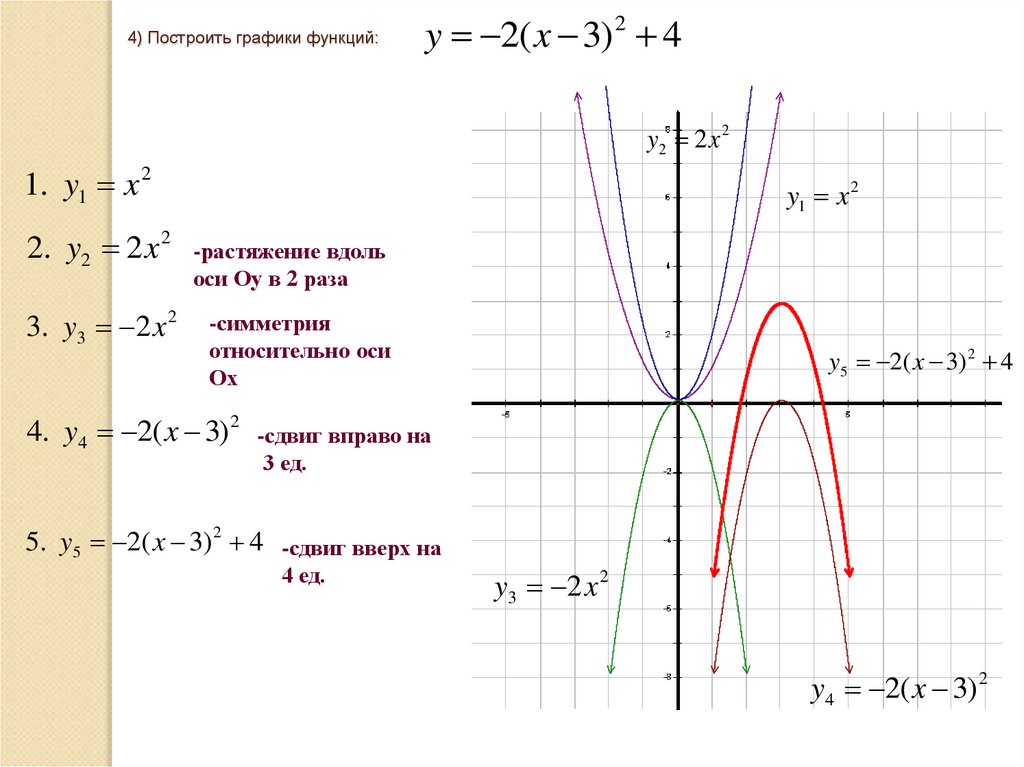
4) Построить графики функций:y 2( x 3) 2 4
y2 2x 2
1. y1 x 2
2. y2 2 x 2
3. y3 2 x 2
y1 x 2
-растяжение вдоль
оси Оу в 2 раза
-симметрия
относительно оси
Ох
y5 2( x 3) 2 4
4. y4 2( x 3) 2 -сдвиг вправо на
3 ед.
5. y5 2( x 3) 2 4 -сдвиг вверх на
4 ед.
y3 2x 2
y4 2( x 3) 2
15.
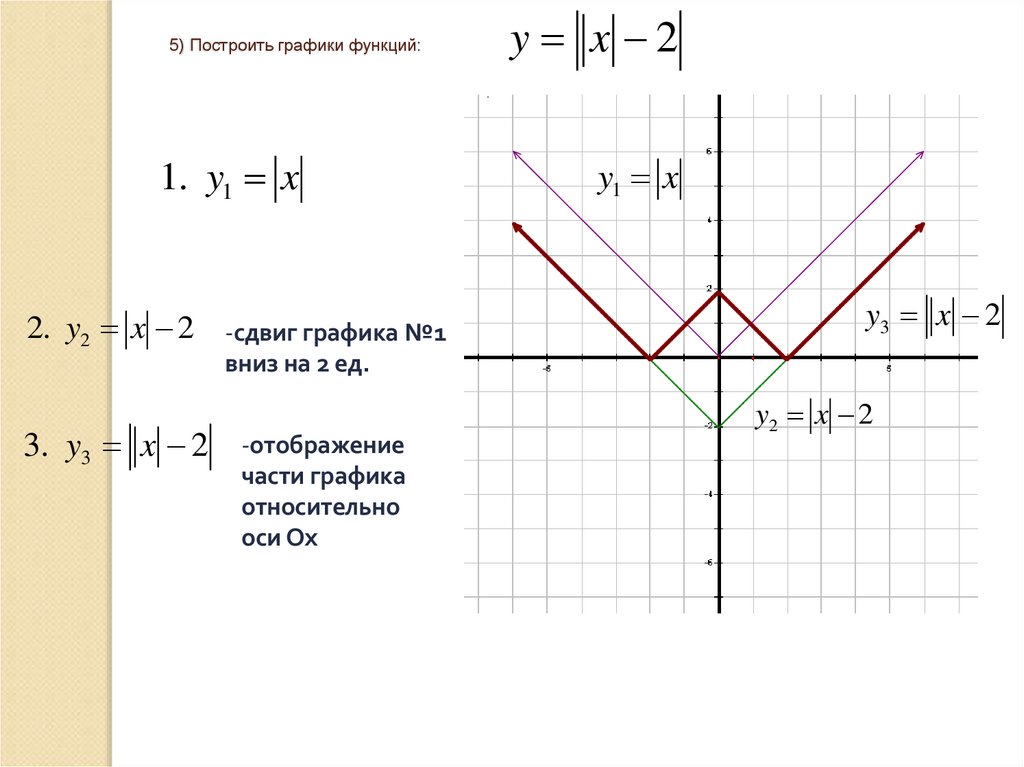
5) Построить графики функций:1. y1 x
2. y2 x 2
3. y3 x 2
-сдвиг графика №1
вниз на 2 ед.
-отображение
части графика
относительно
оси Ох
y x 2
y1 x
y3 x 2
y2 x 2
16.
VI. Построение графиков кусочно-заданных функций.f ( x) ďđč f ( x) a
y
g ( x) ďđč f ( x) a
y f (x)
f ( x) ďđč f ( x) 0
y
f ( x) ďđč f ( x) 0
17.
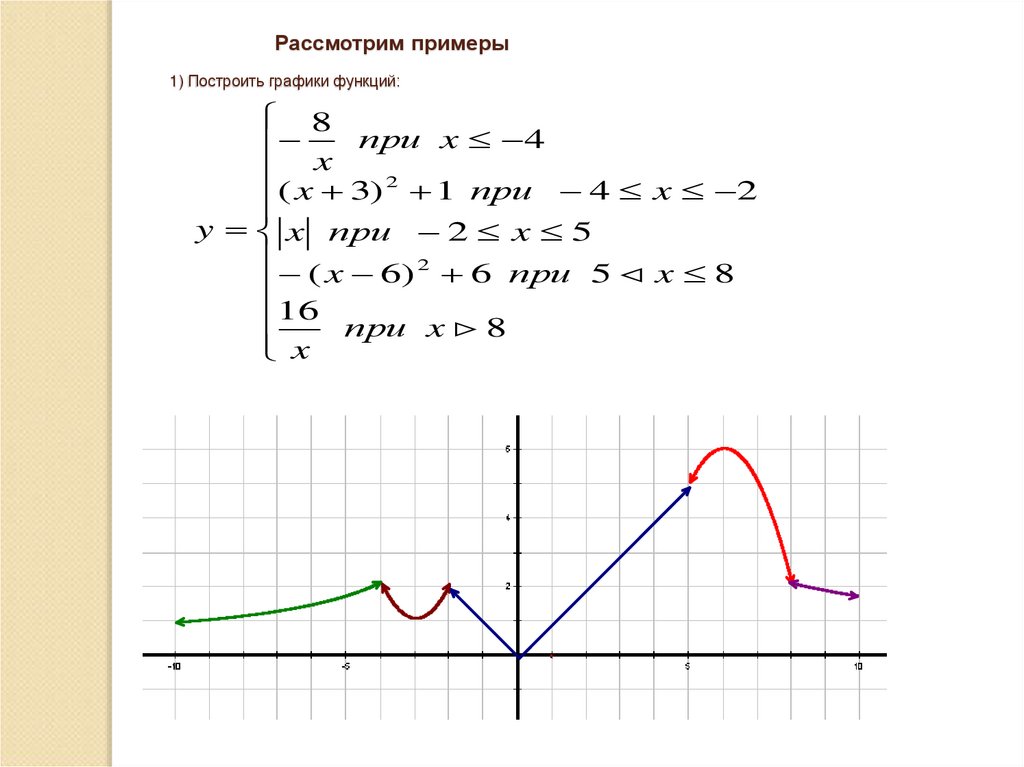
Рассмотрим примеры1) Построить графики функций:
8
при x 4
x
2
( x 3) 1 при 4 x 2
y x при 2 x 5
( x 6) 2 6 при 5 x 8
16
при x 8
x
18.
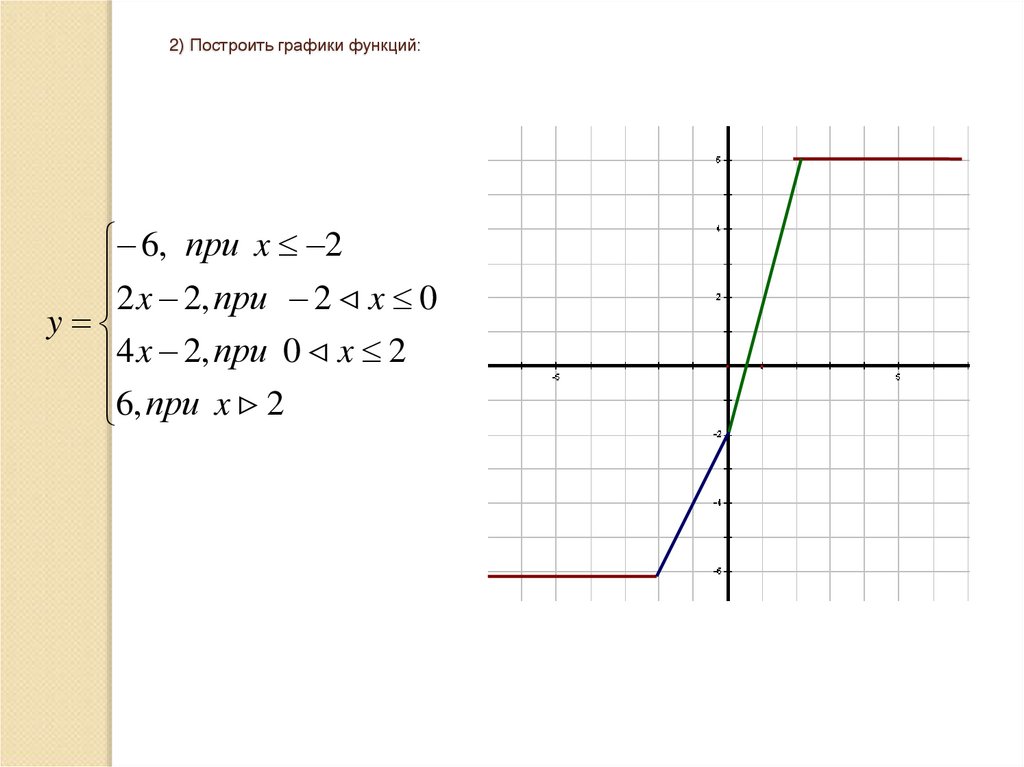
2) Построить графики функций:6, при x 2
2 x 2, при 2 x 0
y
4 x 2, при 0 x 2
6, при x 2
19.
Закрепление:Домашнее задание.
20. Построить графики функций:
21.
Дополнительный материалГрафики улыбаются
22.
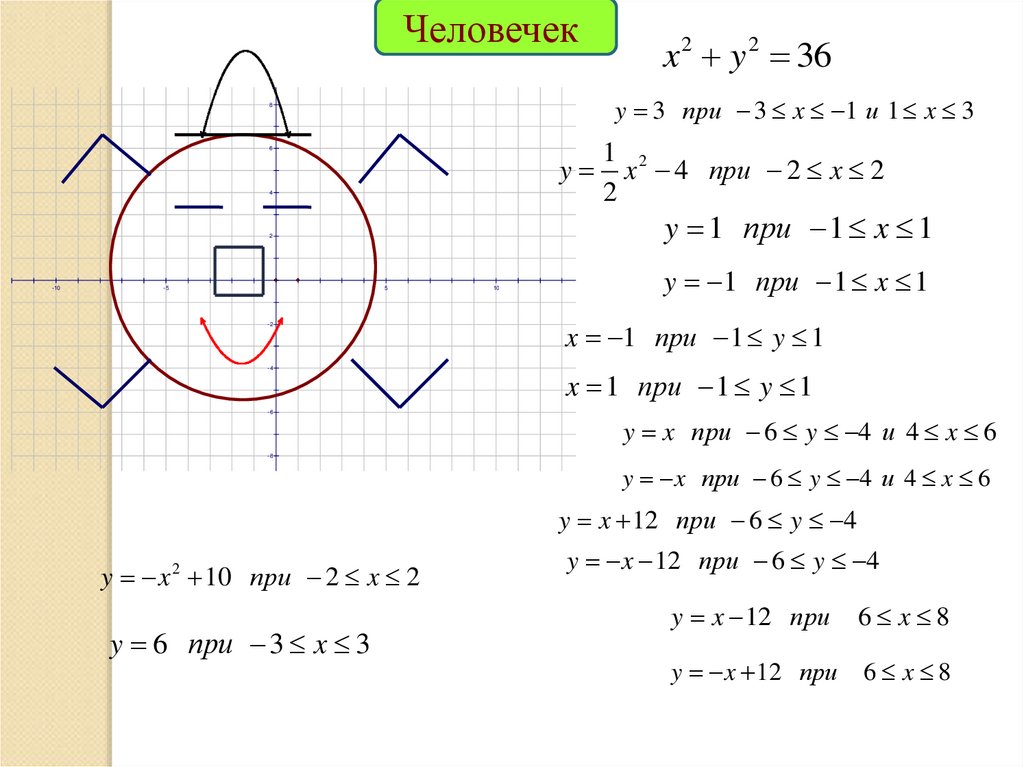
Человечекy 3 при 3 x 1 и 1 x 3
8
6
y
4
5
-5
1 2
x 4 при 2 x 2
2
y 1 при 1 x 1
2
-10
x 2 y 2 36
-2
-4
-6
10
y 1 при 1 x 1
x 1 при 1 y 1
x 1 при 1 y 1
y x при 6 y 4 и 4 x 6
-8
y x при 6 y 4 и 4 x 6
y x 12 при 6 y 4
y x 2 10 при 2 x 2
y 6 при 3 x 3
y x 12 при 6 y 4
y x 12 при
6 x 8
y x 12 при
6 x 8
23.
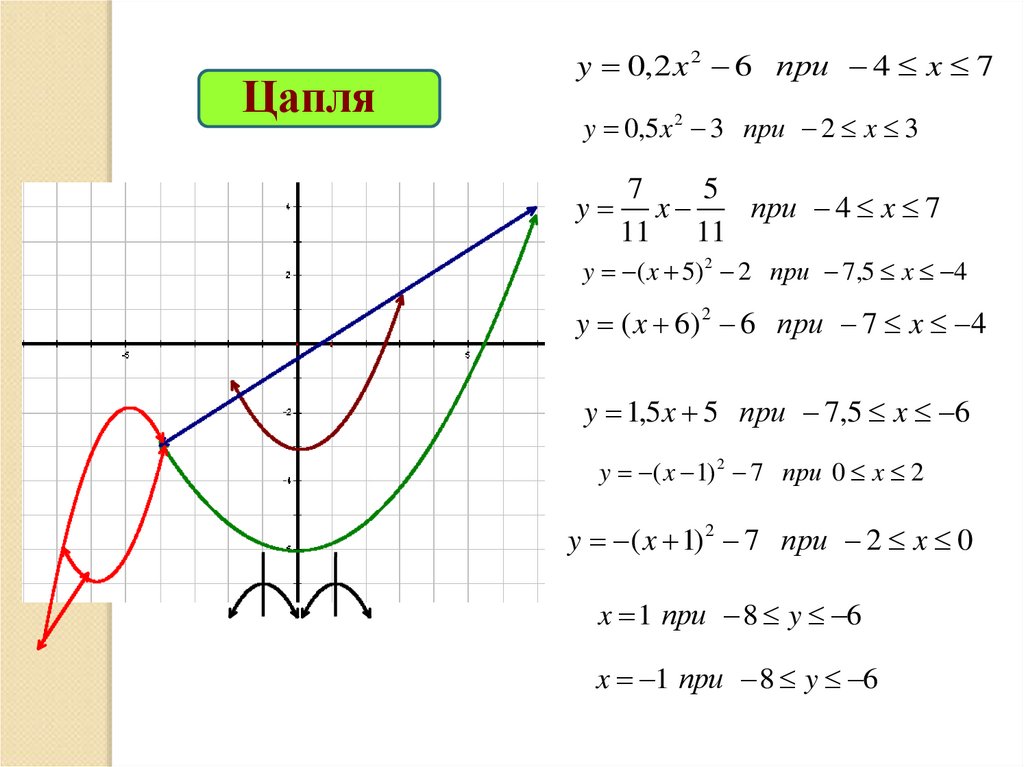
Цапляy 0,2 x 2 6 при 4 x 7
y 0,5 x 2 3 при 2 x 3
y
7
5
x
при 4 x 7
11 11
y ( x 5) 2 2 при 7,5 x 4
y ( x 6) 2 6 при 7 x 4
y 1,5 x 5 при 7,5 x 6
y ( x 1) 2 7 при 0 x 2
y ( x 1) 2 7 при 2 x 0
x 1 при 8 y 6
x 1 при 8 y 6
24.
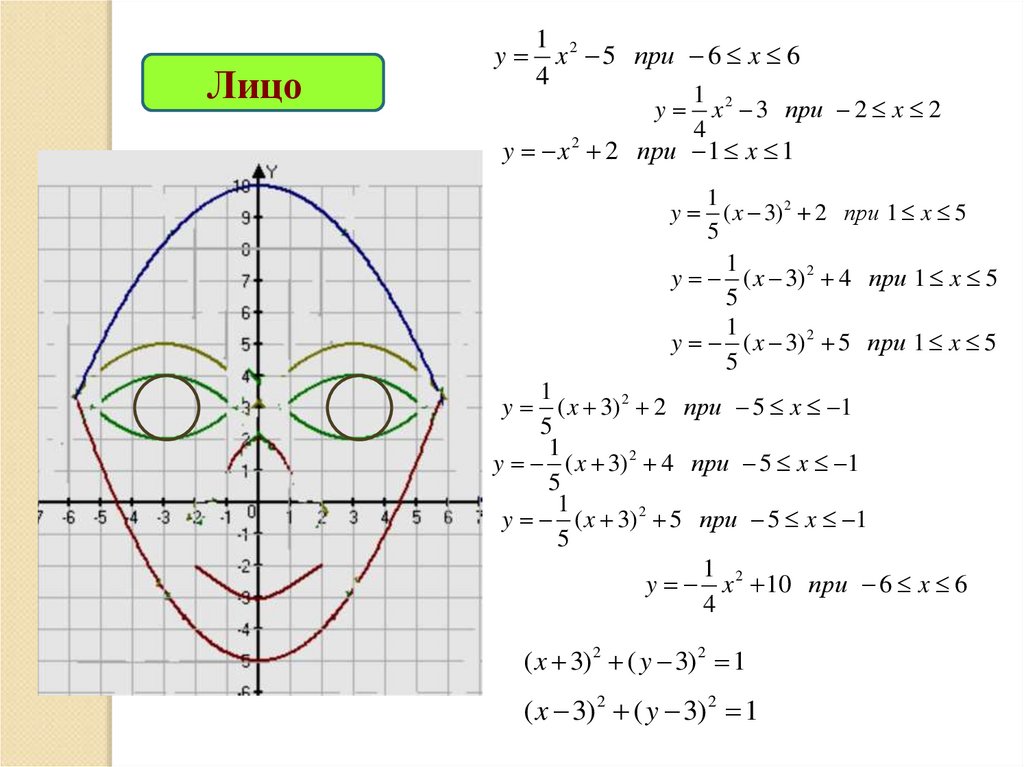
Лицоy
1 2
x 5 при 6 x 6
4
y
1 2
x 3 при 2 x 2
4
y x 2 2 при 1 x 1
1
y ( x 3) 2 2 при 1 x 5
5
1
y ( x 3) 2 4 при 1 x 5
5
1
y ( x 3) 2 5 при 1 x 5
5
1
y ( x 3) 2 2 при 5 x 1
5
1
y ( x 3) 2 4 при 5 x 1
5
1
y ( x 3) 2 5 при 5 x 1
5
1
y x 2 10 при 6 x 6
4
( x 3) 2 ( y 3) 2 1
( x 3) 2 ( y 3) 2 1
25.
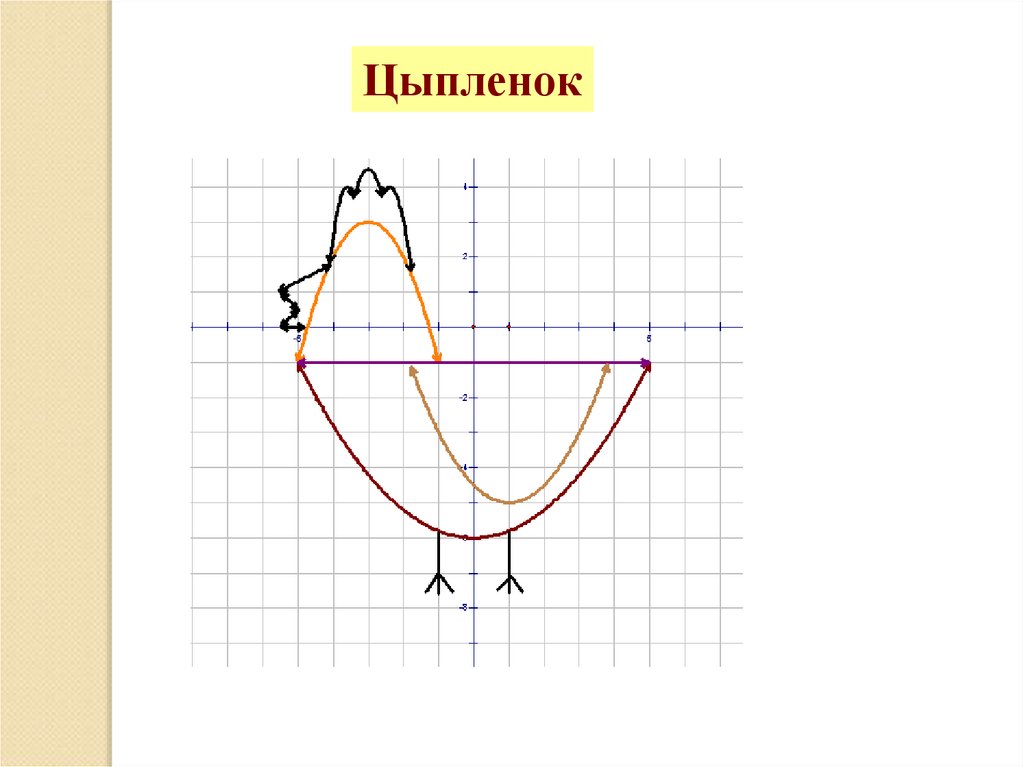
Цыпленок26.
;;
;
;
;
;
;
;
;
;
;
27.
Цветок8
6
4
2
-10
-5
5
-2
-4
-6
-8
10
28.
.,
.
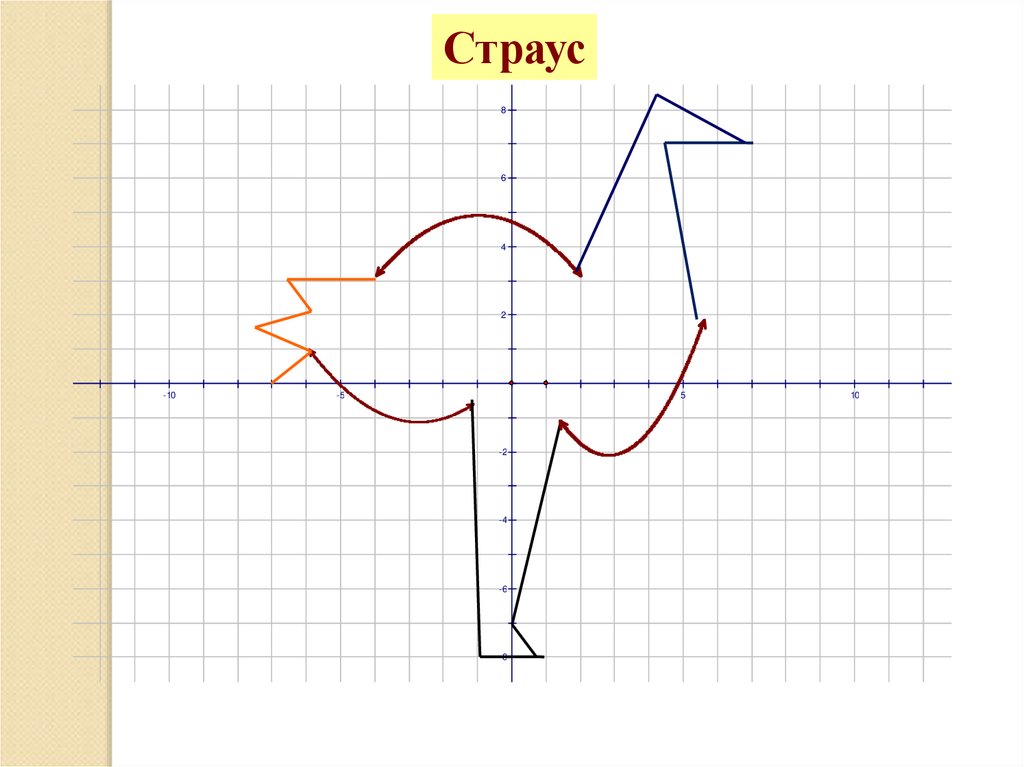
29.
Страус8
6
4
2
-10
-5
5
-2
-4
-6
-8
10
30.
11
1
y ( x 3) 2 1, y ( x 1) 2 4, y ( x 3) 2 2, параболы
3
5
2
3
1
y 5 x 30, y x, y 7, y x 12, шея, голова, клюв
2
2
x 1, y 10, y x 9, y 4 x 9, ноги
1
y 3, y x, y x, y x 7, хвост
2
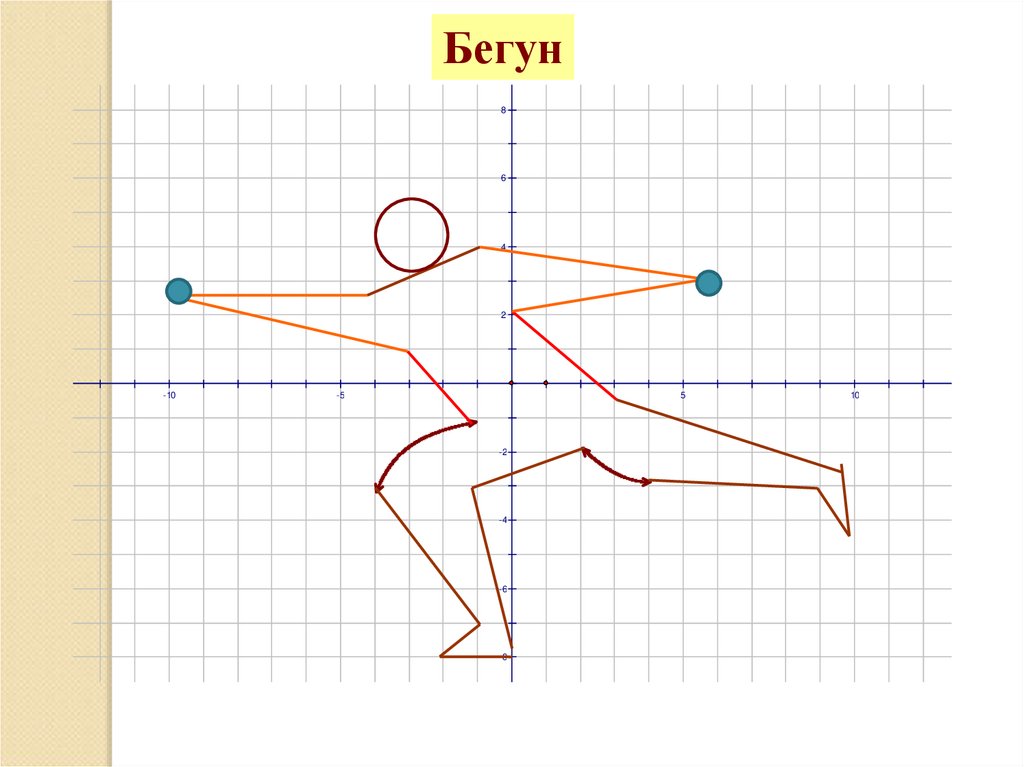
31.
Бегун8
6
4
2
-10
-5
5
-2
-4
-6
-8
10
32.
13
( x 4) 2 3, y
, коленки
4
x 5
( x 2,8) 2 ( y 4,5) 2 0, голова
y
( x 9,6) 2 ( y 2,7) 2 0, ( x 5,8) 2 ( y 3) 2 0, кулаки
1
1
1
y 2,6; y x 0,4; y x 3,8; y x 2, руки
5
5
5
y x 2; y x 2 туловище
1
2
y x 0,5; y 2; y x 7; x 9,8 правая нога
5
3
1
2
1
y x 2,7; y x 8,3; y x 8; y x; x 8 левая нога
3
3
5
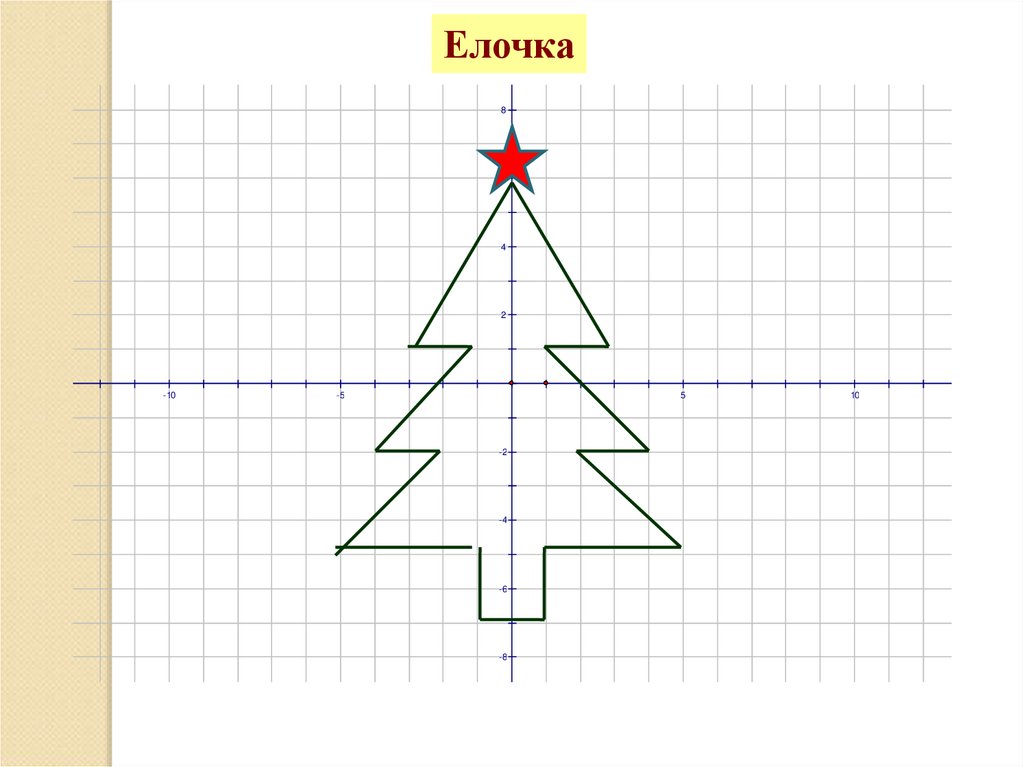
33.
Елочка8
6
4
2
-10
-5
5
-2
-4
-6
-8
10
34.
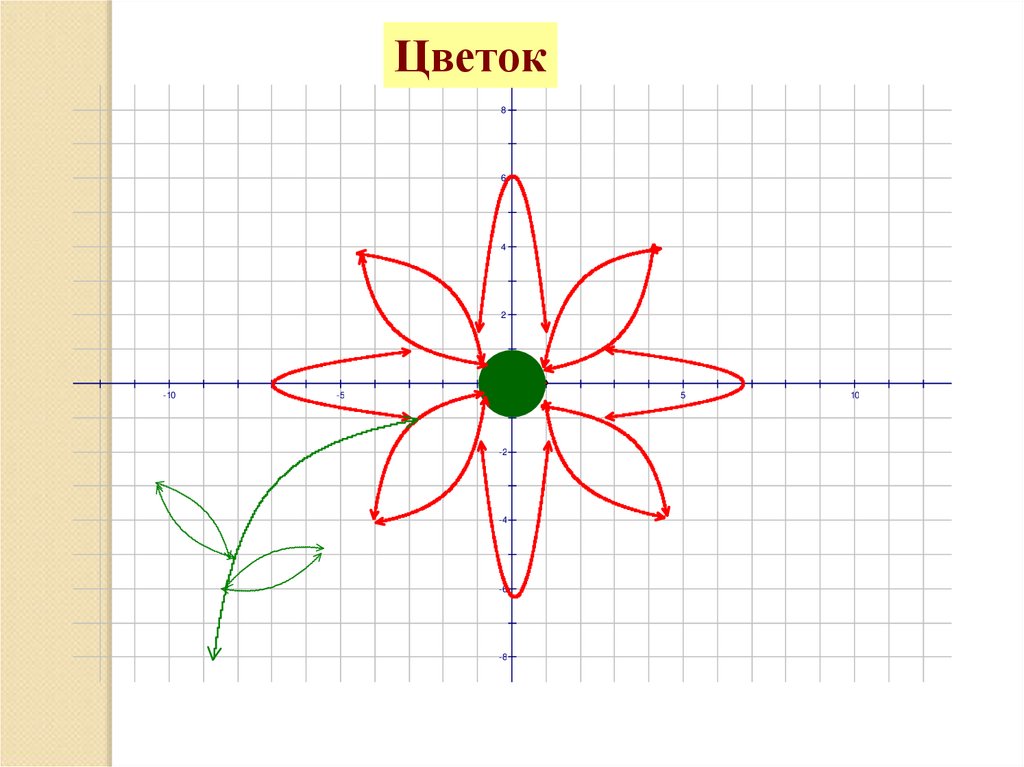
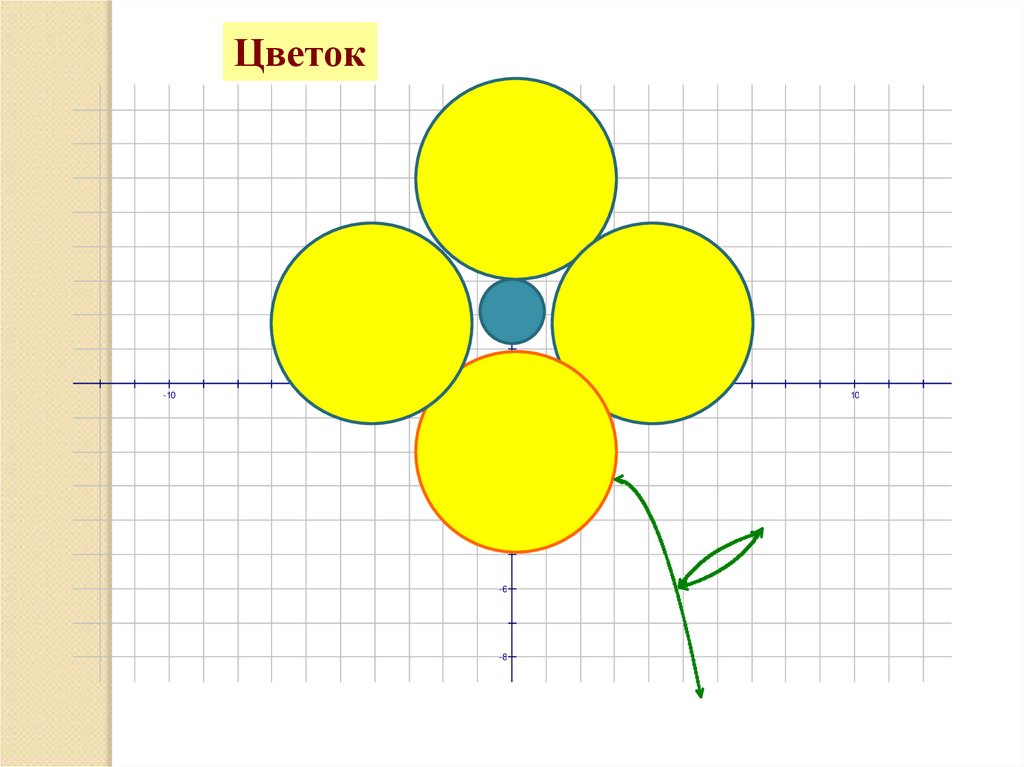
Цветок8
6
4
2
-10
-5
5
-2
-4
-6
-8
10
35.
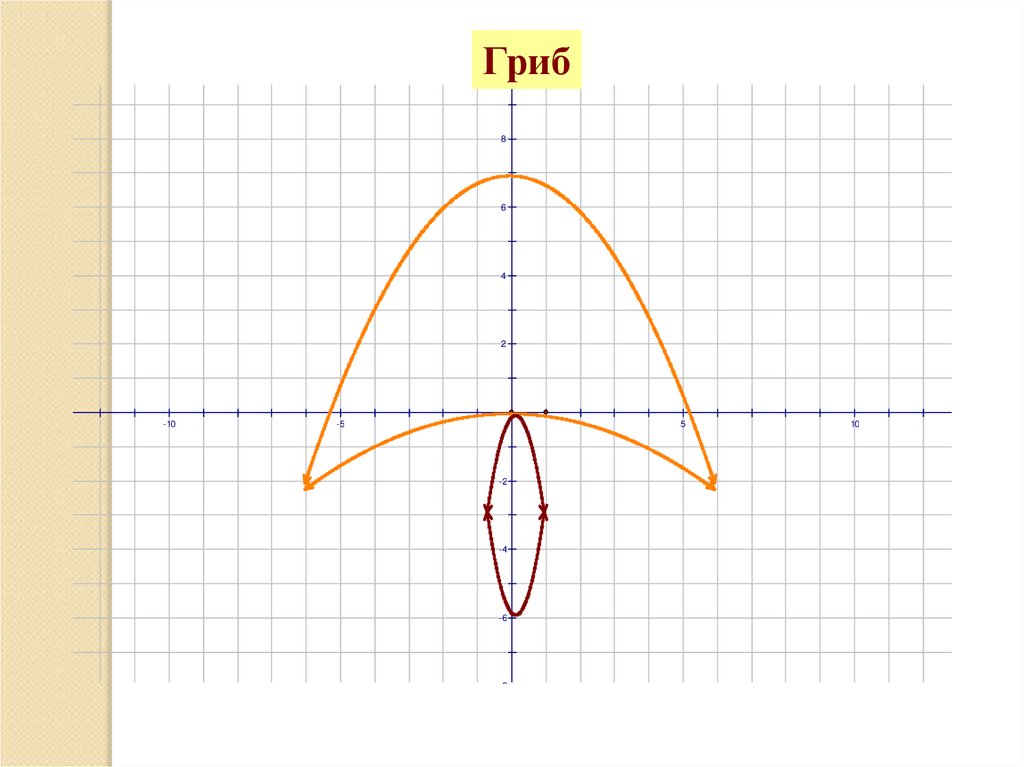
Гриб8
6
4
2
-10
-5
5
-2
-4
-6
-8
10
36.
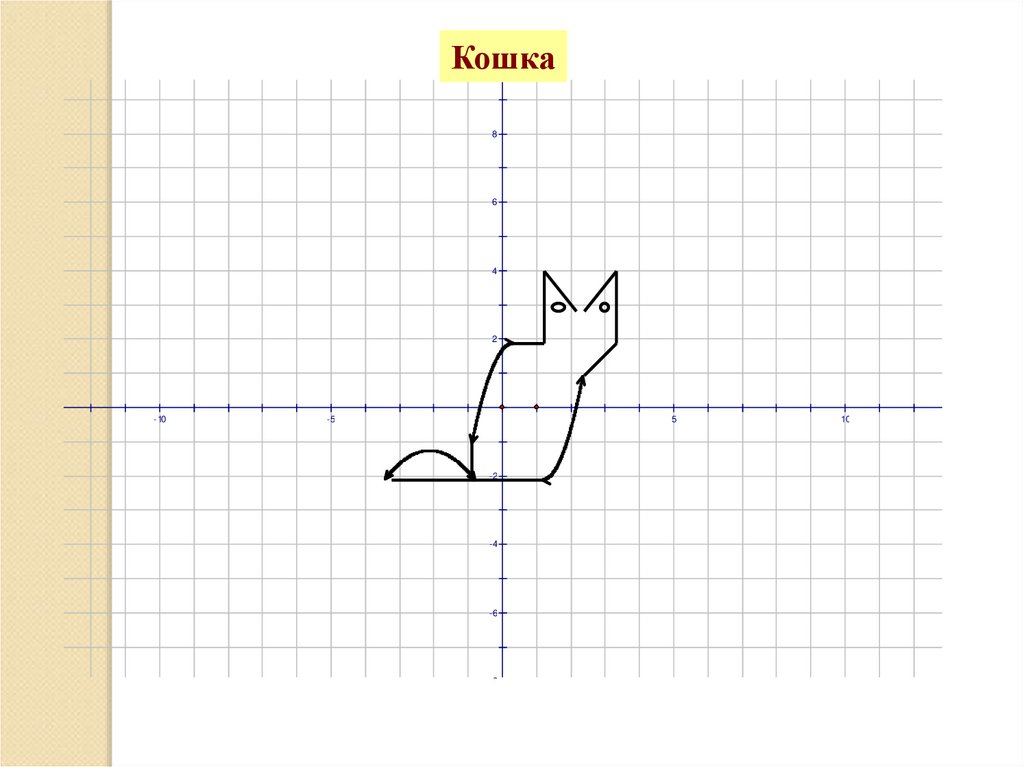
Кошка8
6
4
2
-10
-5
5
-2
-4
-6
-8
10
37.
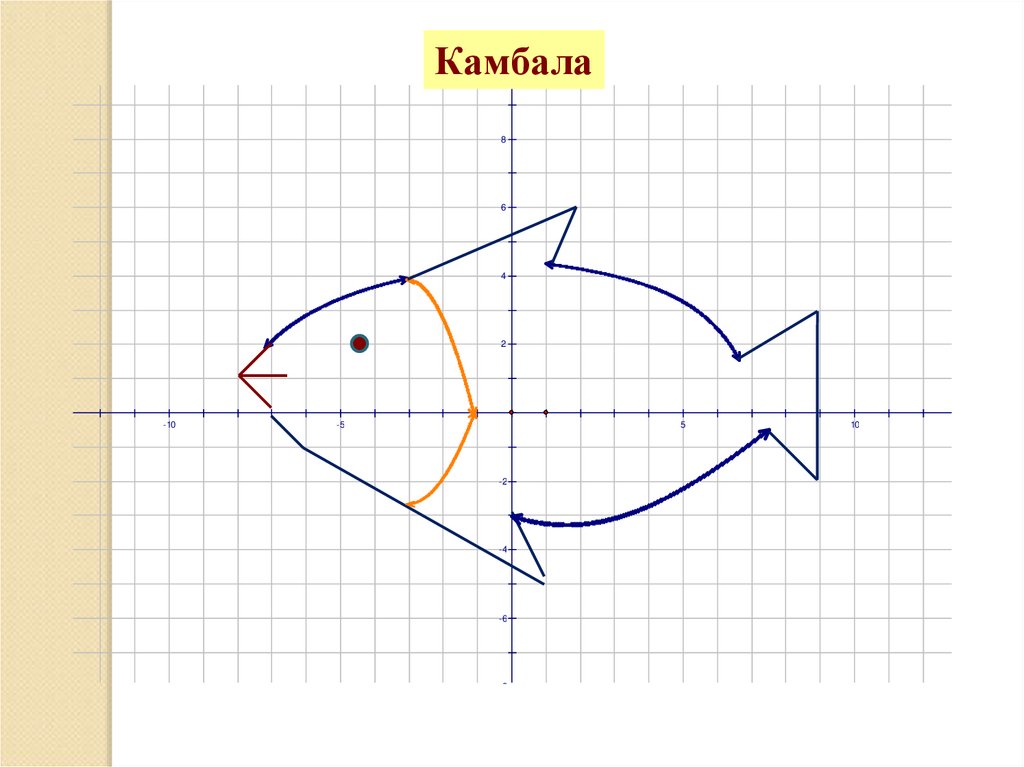
Камбала8
6
4
2
-10
-5
5
-2
-4
-6
-8
10
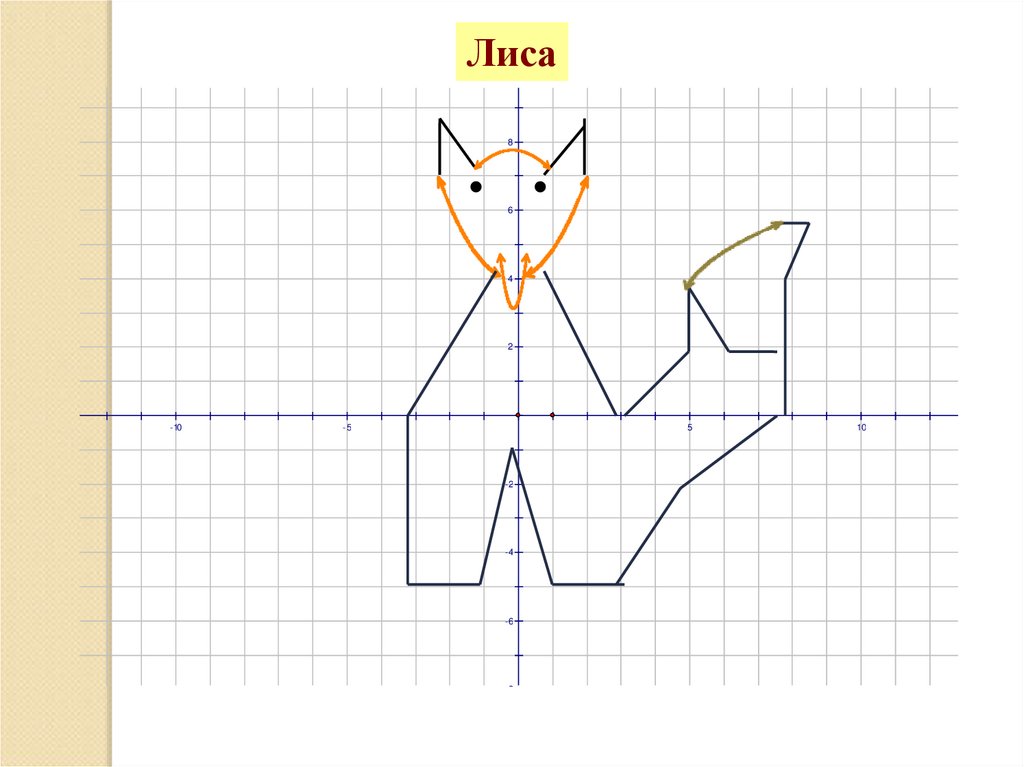
38.
Лиса8
6
4
2
-10
-5
5
-2
-4
-6
-8
10
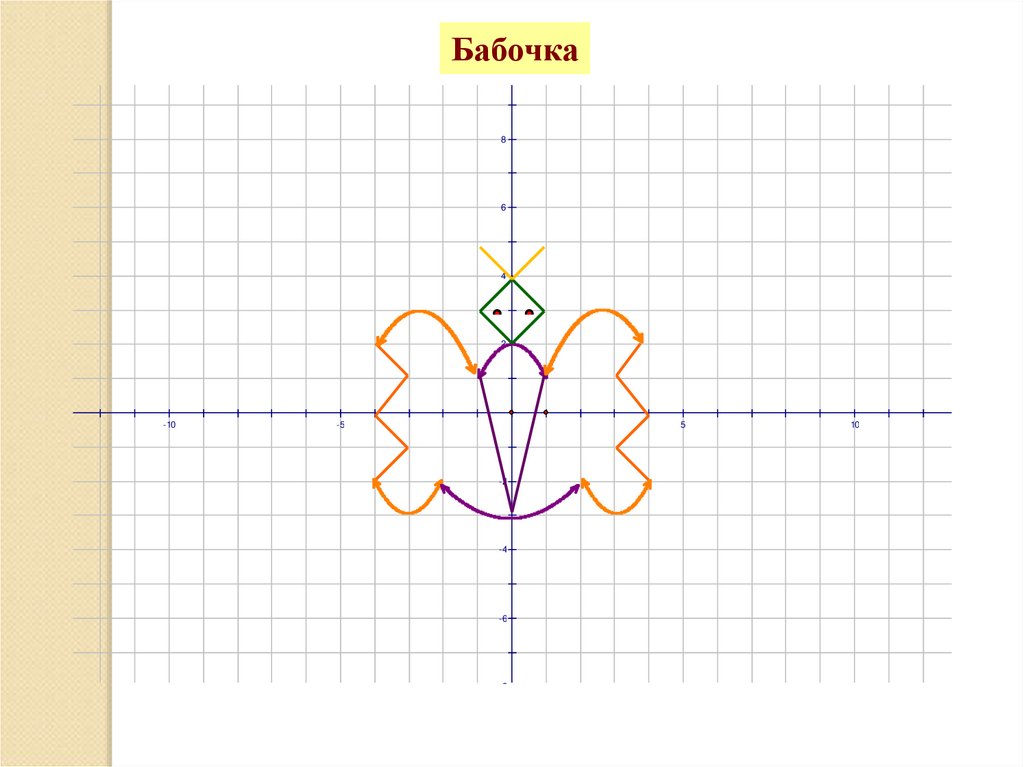
39.
Бабочка8
6
4
2
-10
-5
5
-2
-4
-6
-8
10
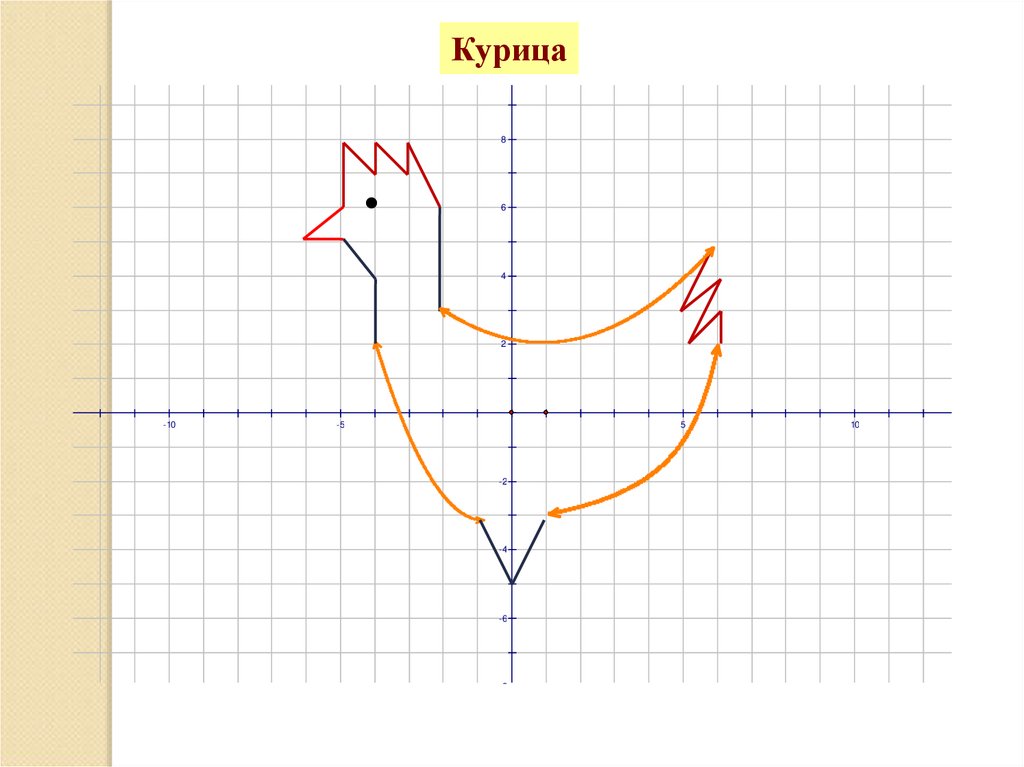
40.
Курица8
6
4
2
-10
-5
5
-2
-4
-6
-8
10
41.
Использованные материалы:1. Мордкович А.Г., Семенов П.В. Алгебра 8 класс,
часть 1, учебник для учащихся
общеобразовательных учреждений – Москва:
Мнемозина, 2011
2. Программа для построения графиков Advanced
Grapfer 2.2
3. Виртуальный конструктор «Живая математика» -
Москва: Институт новых технологий, 2012







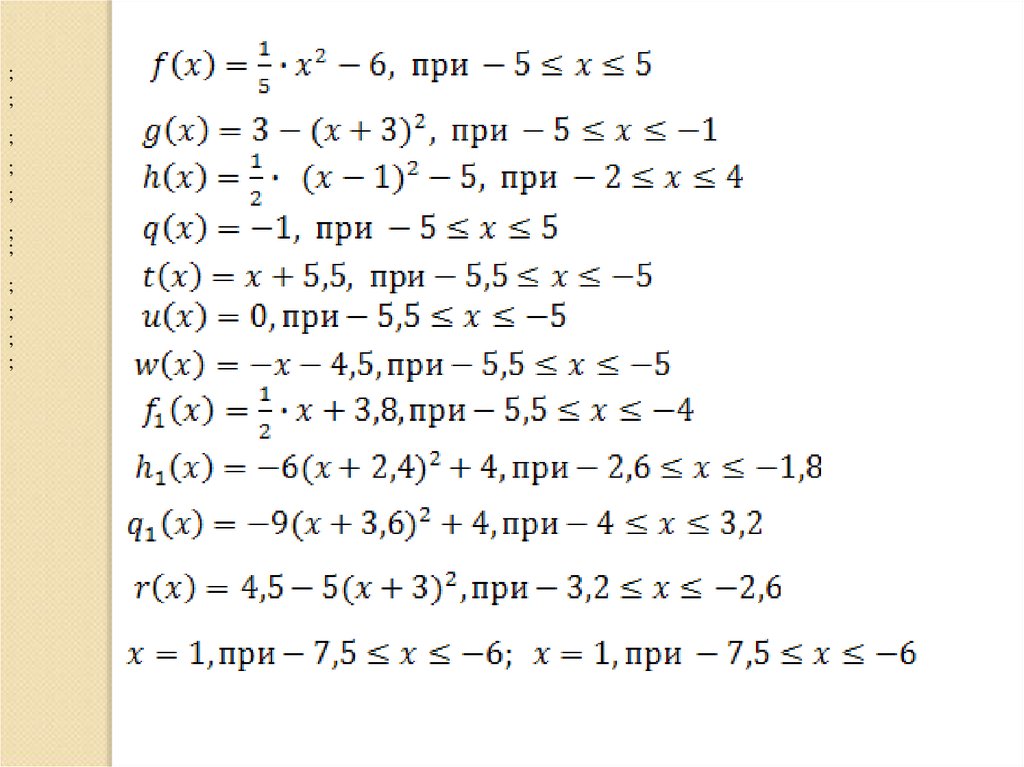
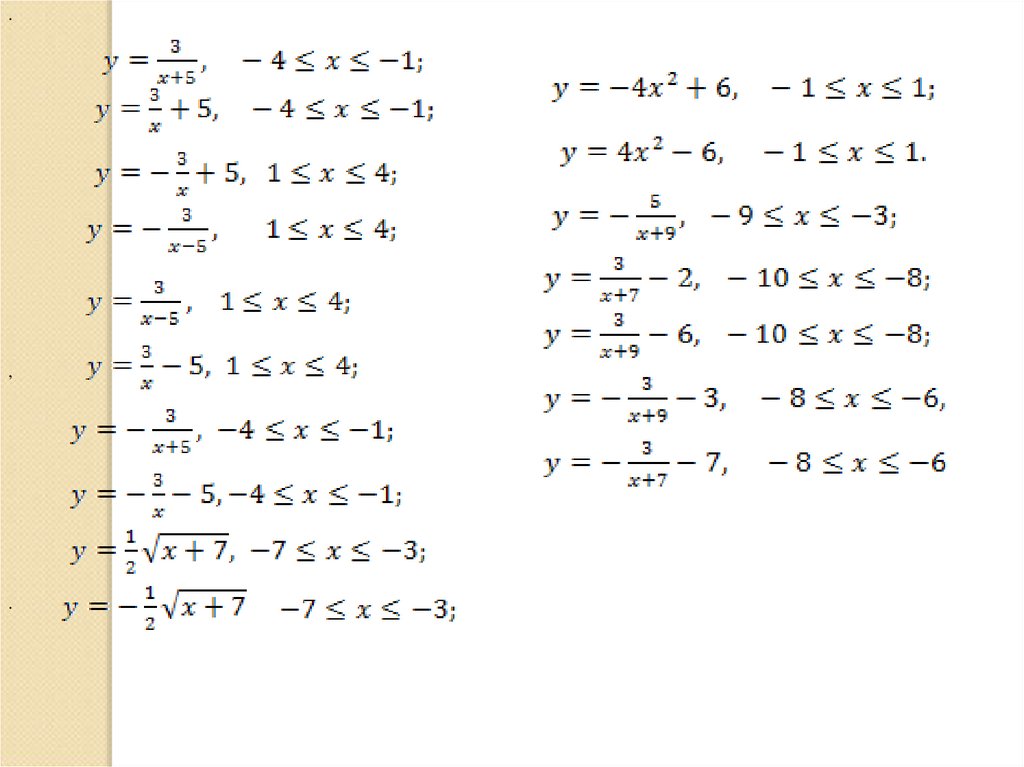



 mathematics
mathematics








