4. Проецирование прямых(1)

1. Проецирование прямых

ГАПОУ СО «Уральский колледж строительства, архитектуры и
предпринимательства»
Проецирование прямых
Екатеринбург 2010

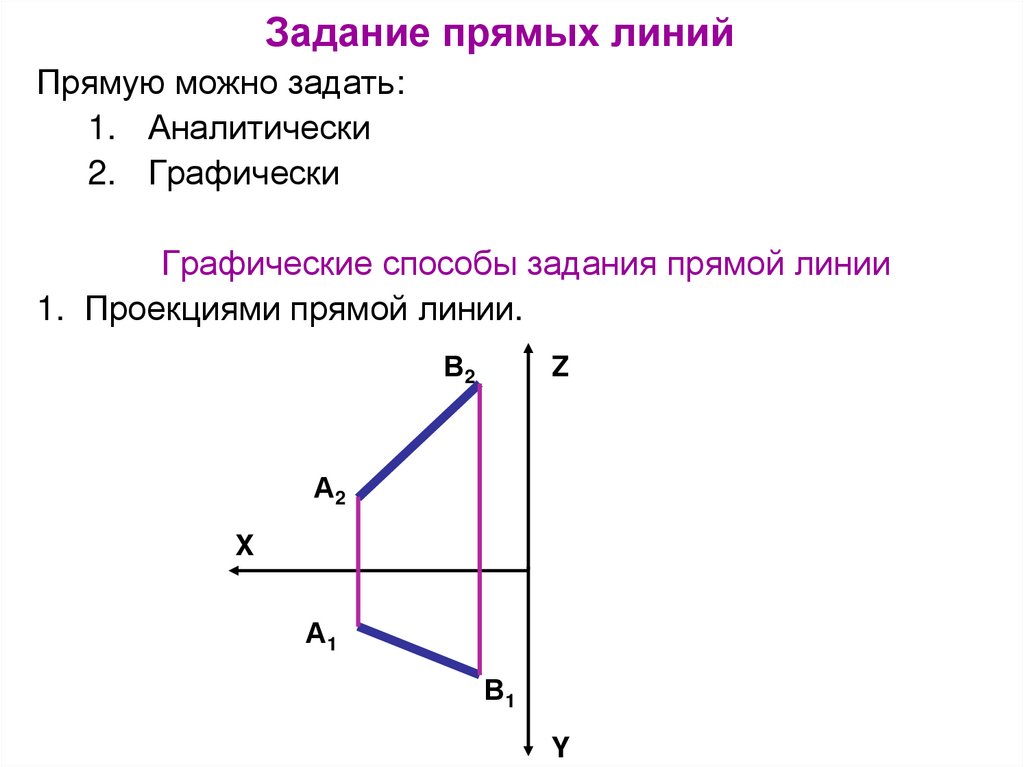
2. Задание прямых линий

Прямую можно задать:
1. Аналитически
2. Графически
Графические способы задания прямой линии
1. Проекциями прямой линии.
В2
Z
А2
X
А1
В1
Y

3.

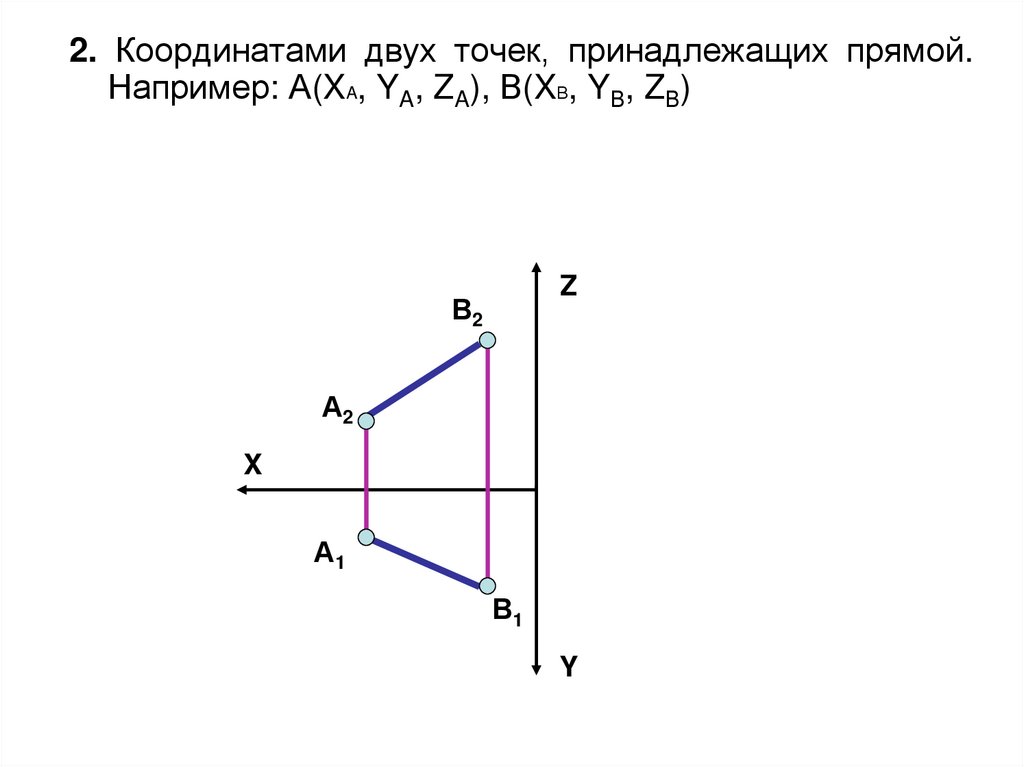
2. Координатами двух точек, принадлежащих прямой.
Например: А(XA, YA, ZA), В(XВ, YВ, ZВ)
Z
В2
А2
X
А1
В1
Y

4.

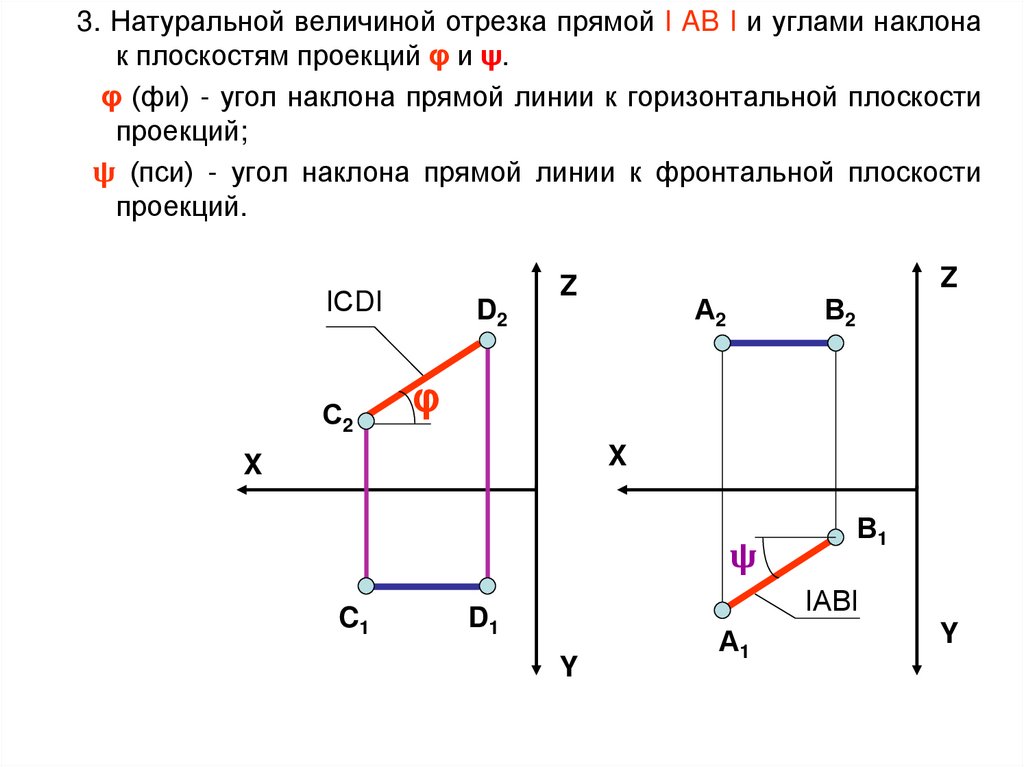
3. Натуральной величиной отрезка прямой I AB I и углами наклона
к плоскостям проекций φ и ψ.
φ (фи) - угол наклона прямой линии к горизонтальной плоскости
проекций;
ψ (пси) - угол наклона прямой линии к фронтальной плоскости
проекций.
IСDI
С2
D2
Z
Z
А2
В2
φ
X
X
ψ
C1
В1
IАВI
D1
Y
А1
Y

5. Ортогональные проекции прямой линии

1.В зависимости от положения относительно плоскостей проекций
прямые линии разделяют на:
• прямые частного положения
• прямые общего положения
2. Прямые частного положения разделяют на:
• прямые, параллельные плоскостям проекций, –
линии уровня;
• прямые, перпендикулярные плоскостям проекций, –
проецирующие прямые.
3. Прямые общего положения - прямые, не параллельные и не
перпендикулярные плоскостям проекций
.

6.

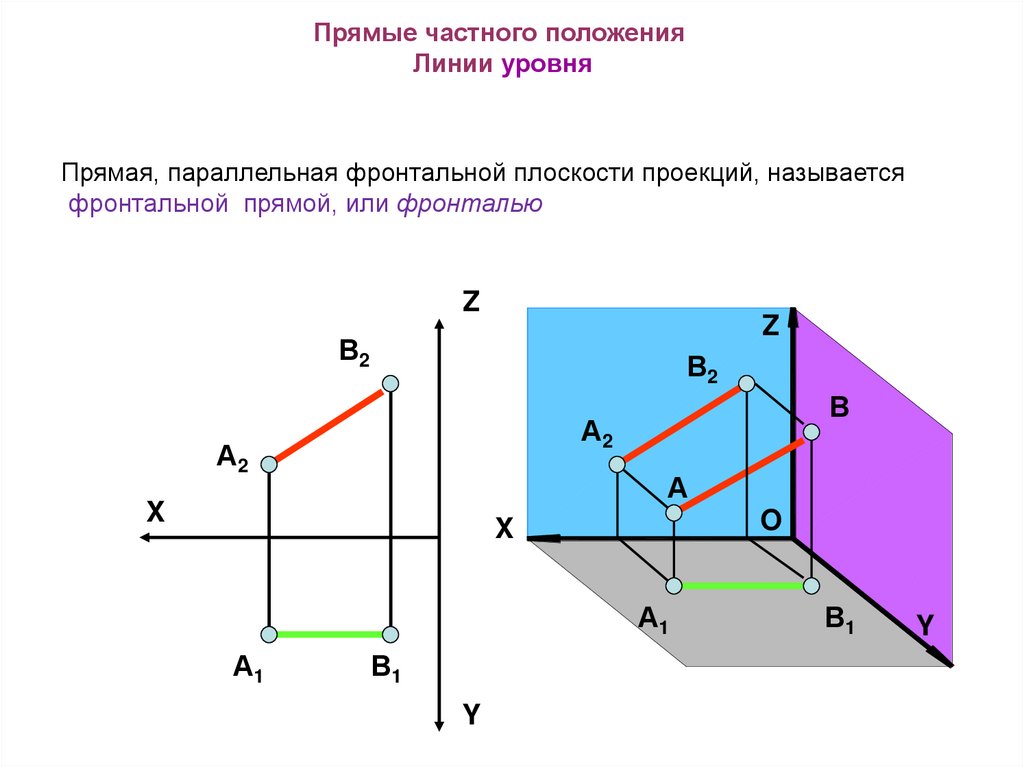
Прямые частного положения
Линии уровня
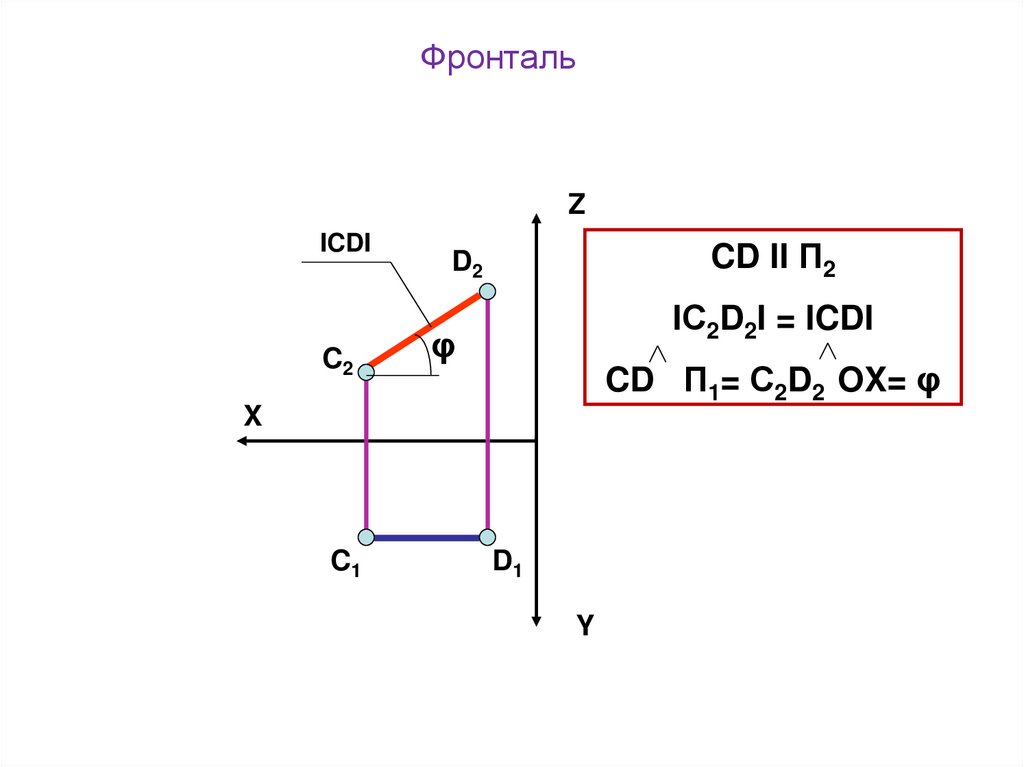
Прямая, параллельная фронтальной плоскости проекций, называется
фронтальной прямой, или фронталью
Z
Z
В2
В2
В
А2
А2
А
X
O
X
А1
А1
В1
Y
В1
Y

7.

Фронталь
Z
ICDI
C2
CD II П2
D2
IС2D2I = ICDI
φ
CD П1= С2D2 OX= φ
X
C1
D1
Y

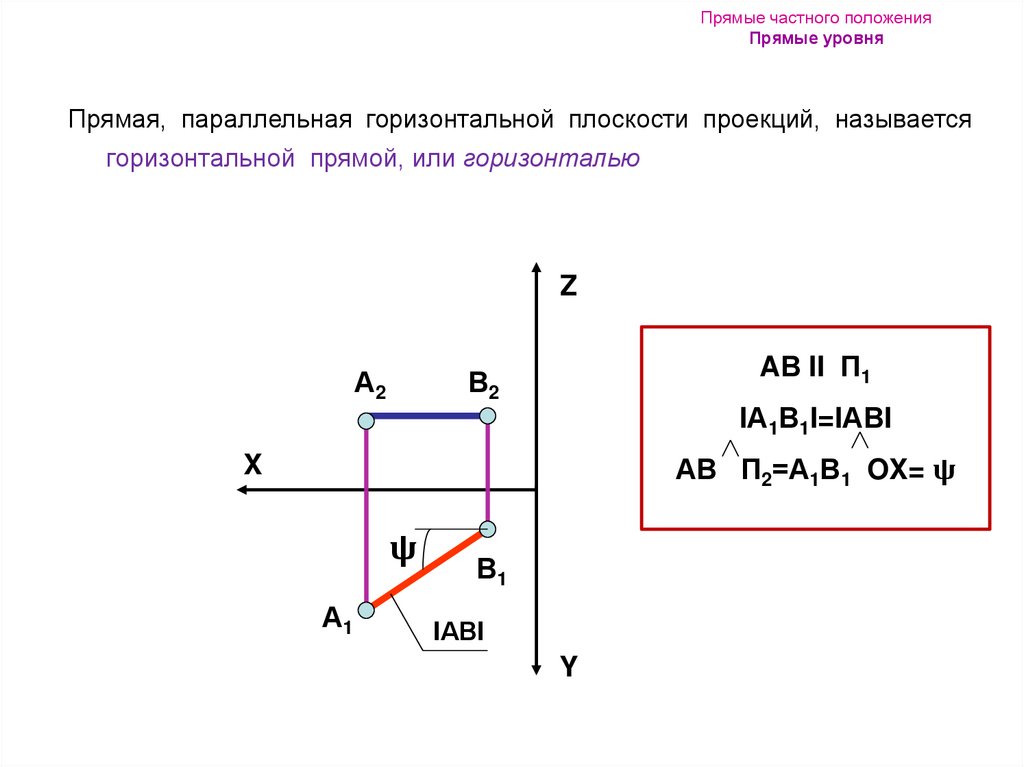
8. Прямые частного положения Прямые уровня

Прямая, параллельная горизонтальной плоскости проекций, называется
горизонтальной прямой, или горизонталью
Z
А2
AВ II П1
В2
IА1В1I=IАВI
АВ П2=А1В1 OX= ψ
X
ψ
А1
В1
IАВI
Y

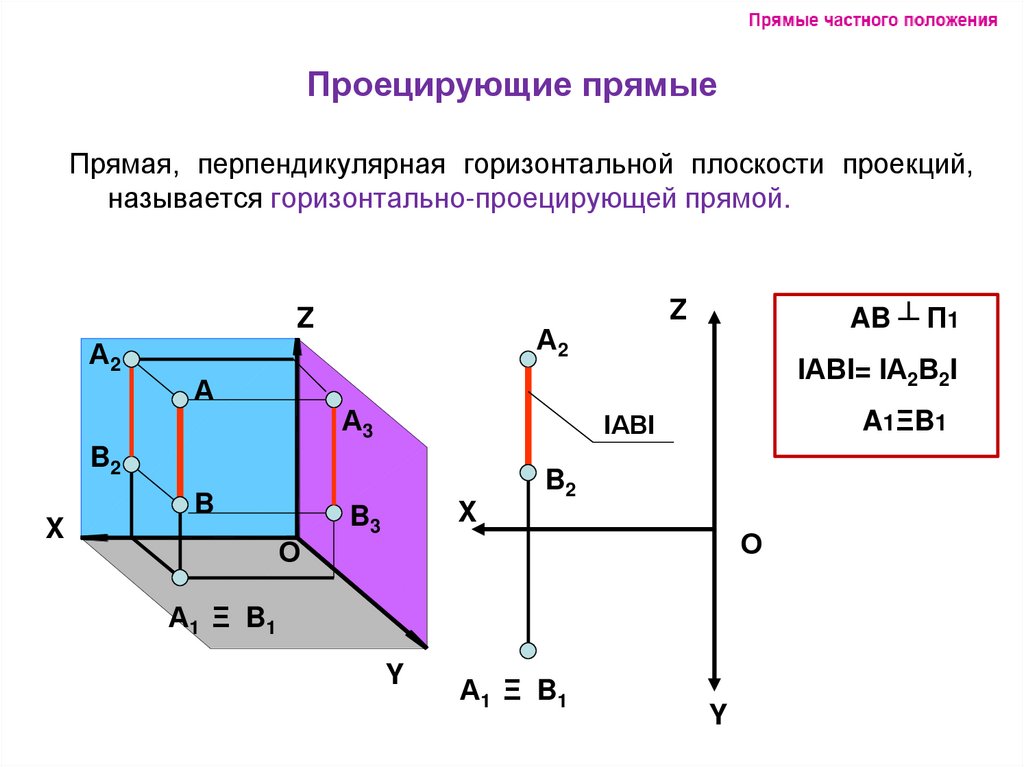
9. Проецирующие прямые

Прямая, перпендикулярная горизонтальной плоскости проекций,
называется горизонтально-проецирующей прямой.
Z
А2
А
А2
А3
AB ┴ П1
IАВI= IА2В2I
A1ΞB1
IАВI
B2
X
Z
B2
B
О
X
B3
О
А1 Ξ B 1
Y
А1 Ξ B1
Y

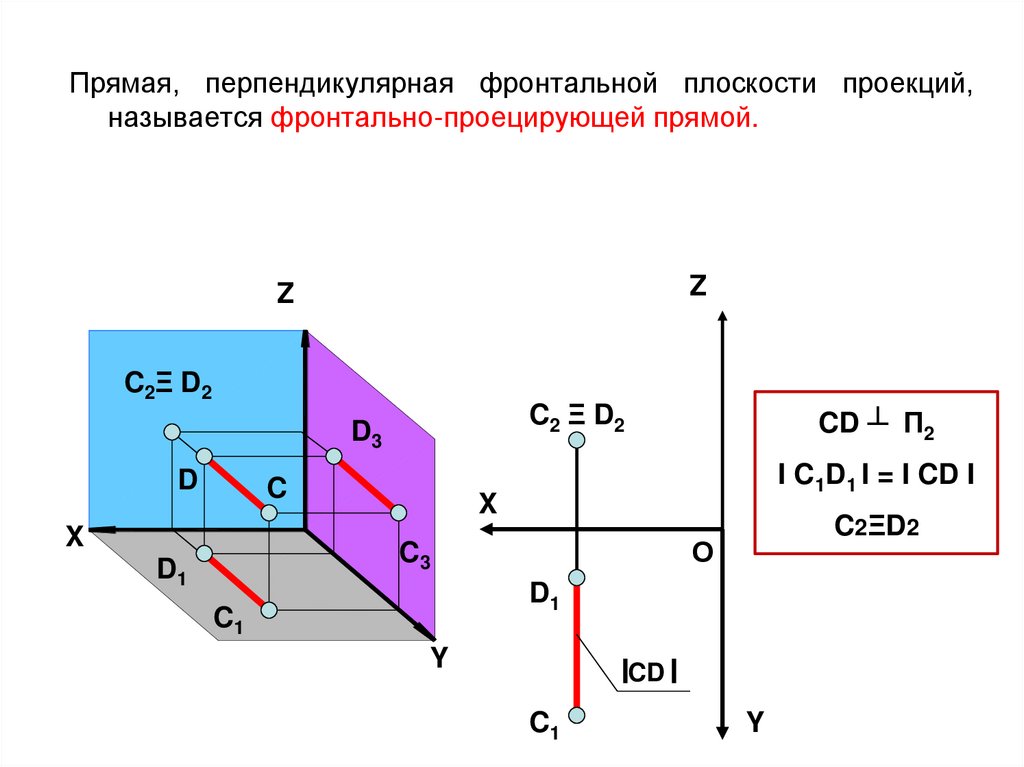
10.

Прямая, перпендикулярная фронтальной плоскости проекций,
называется фронтально-проецирующей прямой.
Z
Z
C2Ξ D2
C2 Ξ D2
D3
D
C
X
CD ┴ П2
I C1D1 I = I CD I
X
О
C3
D1
C2ΞD2
D1
C1
Y
CD
C1
Y

11. Прямые линии общего положения -

Прямые линии общего положения прямые, не параллельные и не
перпендикулярные
плоскостям
проекций

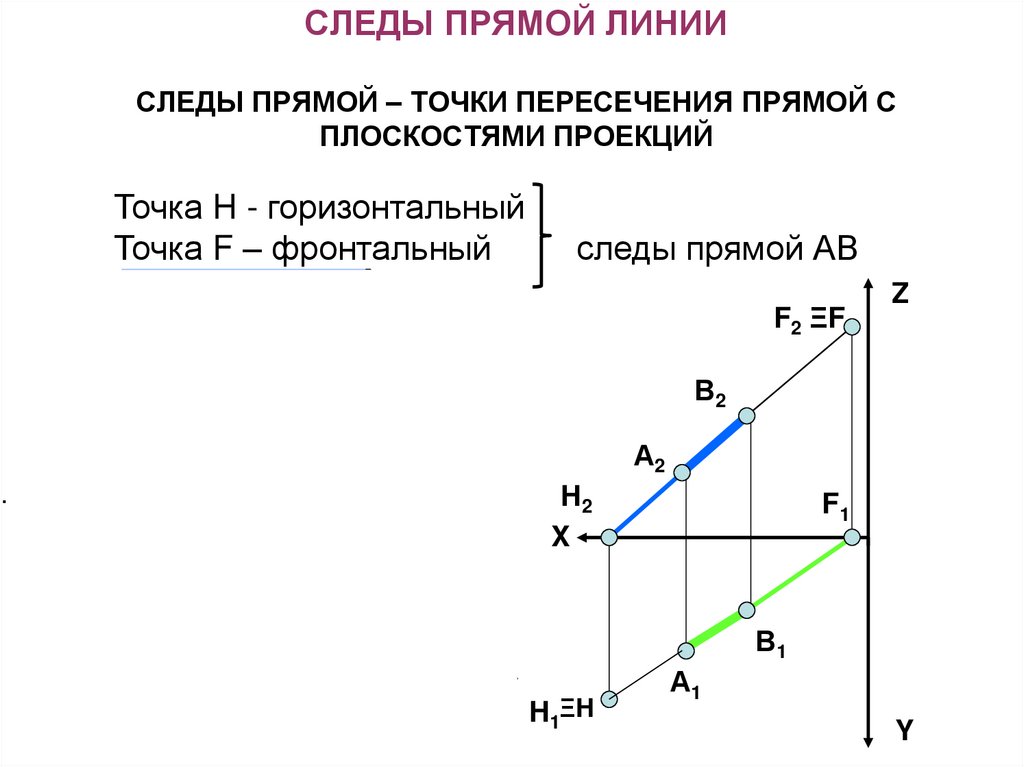
12. СЛЕДЫ ПРЯМОЙ ЛИНИИ СЛЕДЫ ПРЯМОЙ – ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПЛОСКОСТЯМИ ПРОЕКЦИЙ

Точка H - горизонтальный
Точка F – фронтальный
П2
следы прямой АВ
Z
F2 ΞF
В2 F2ΞF
А2
.
H2
В2
П3
B
F1
H1ΞH
А1
А2
H2
X
А
X
Z
F1
В1
В1
П1
Y
H1ΞH
А1
Y

13. Относительное положение прямых

Прямые относительно друг друга могут
располагаться:
1. Параллельно
2. Перпендикулярно
3. Пересекаться
4. Скрещиваться

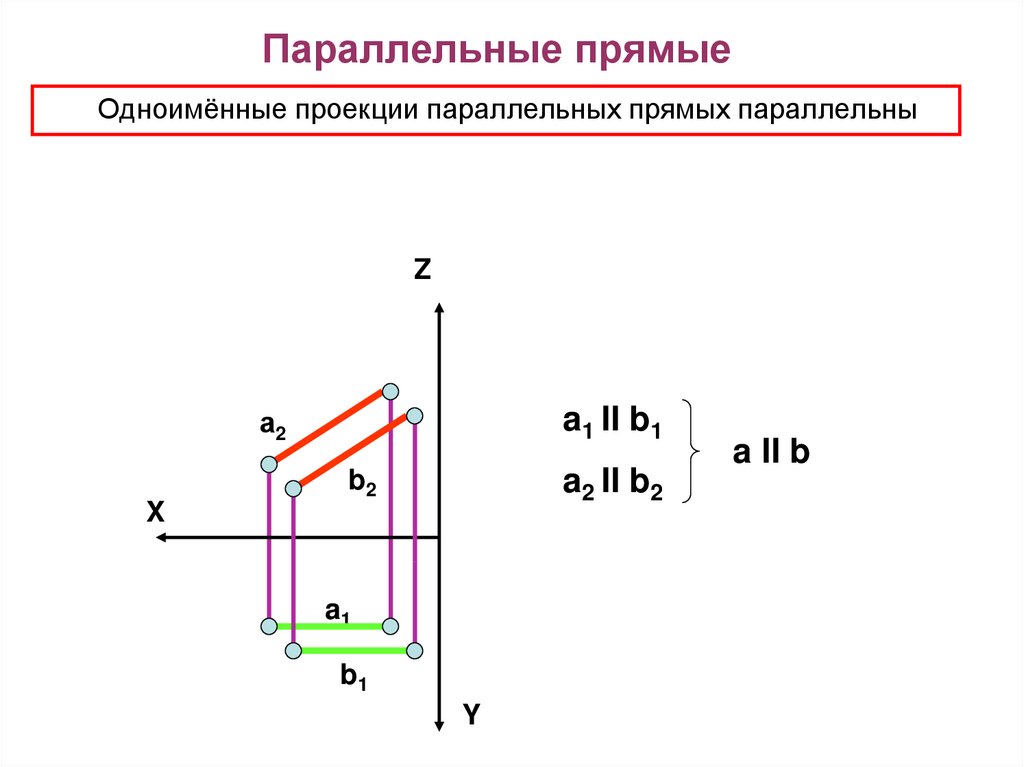
14. Параллельные прямые

Одноимённые проекции параллельных прямых параллельны
Z
a1 II b1
а2
a2 II b2
b2
X
a1
b1
Y
a II b

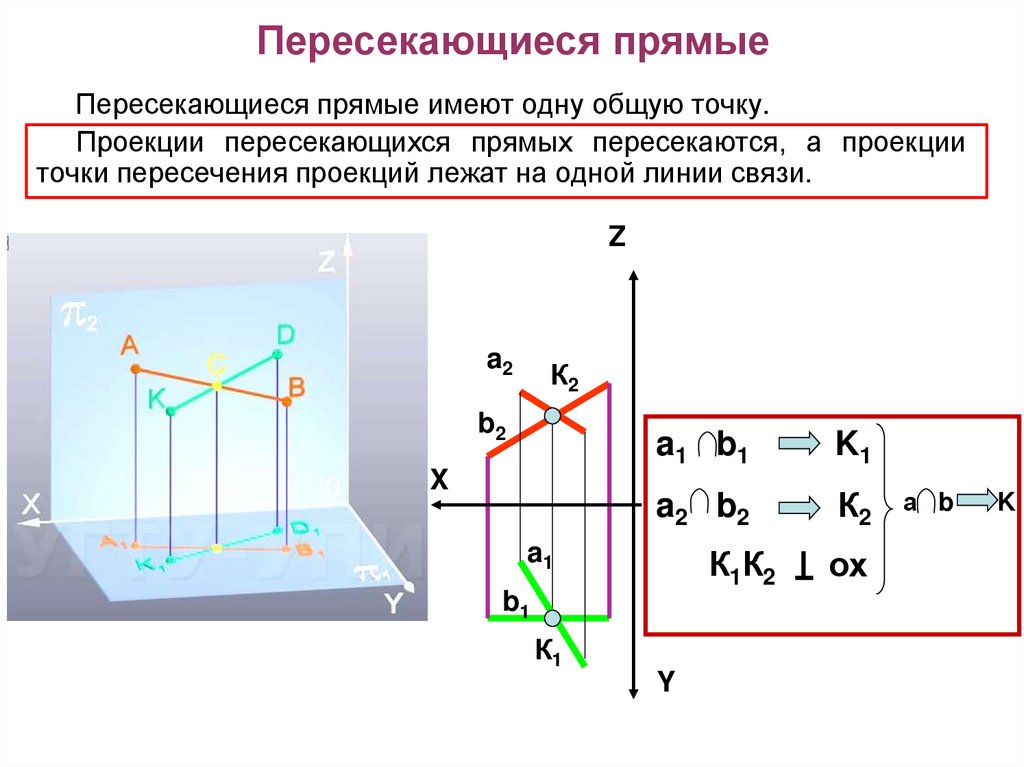
15. Пересекающиеся прямые

Пересекающиеся прямые имеют одну общую точку.
Проекции пересекающихся прямых пересекаются, а проекции
точки пересечения проекций лежат на одной линии связи.
Z
a2
К2
b2
X
a1 b1
K1
a2 b2
К2
a1
К1К2
b1
К1
Y
ох
а b
K

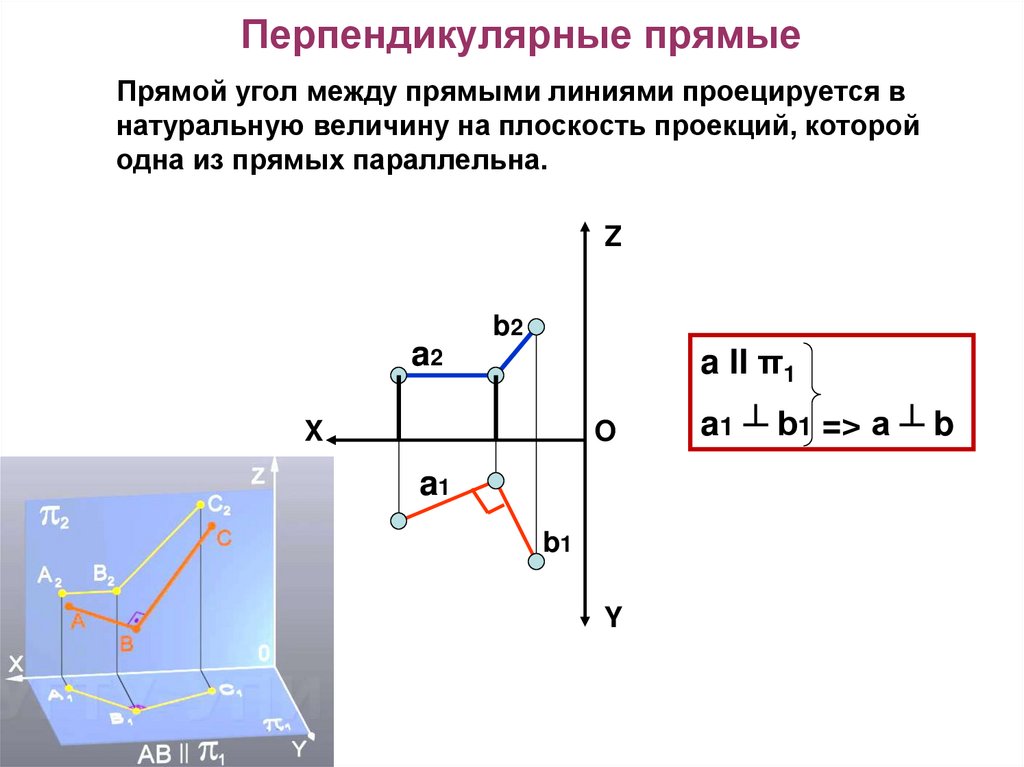
16. Перпендикулярные прямые

Прямой угол между прямыми линиями проецируется в
натуральную величину на плоскость проекций, которой
одна из прямых параллельна.
Z
a2
b2
a II π1
X
O
a1
b1
Y
a1 ┴ b1 => a ┴ b

17.

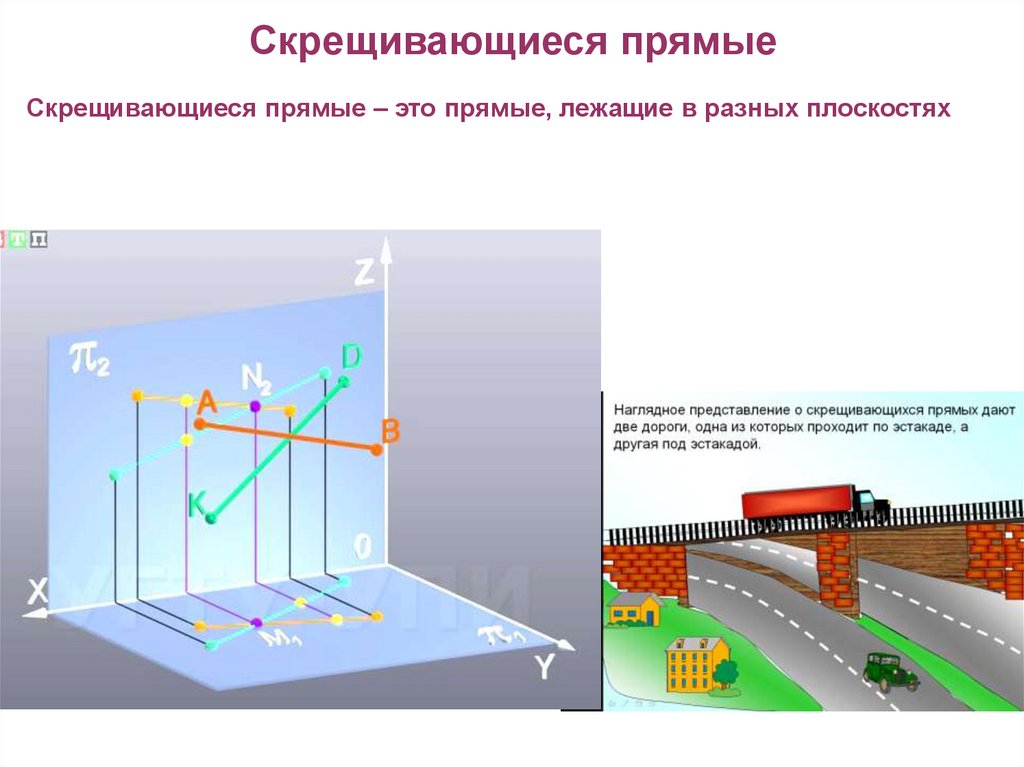
Скрещивающиеся прямые
Скрещивающиеся прямые – это прямые, лежащие в разных плоскостях

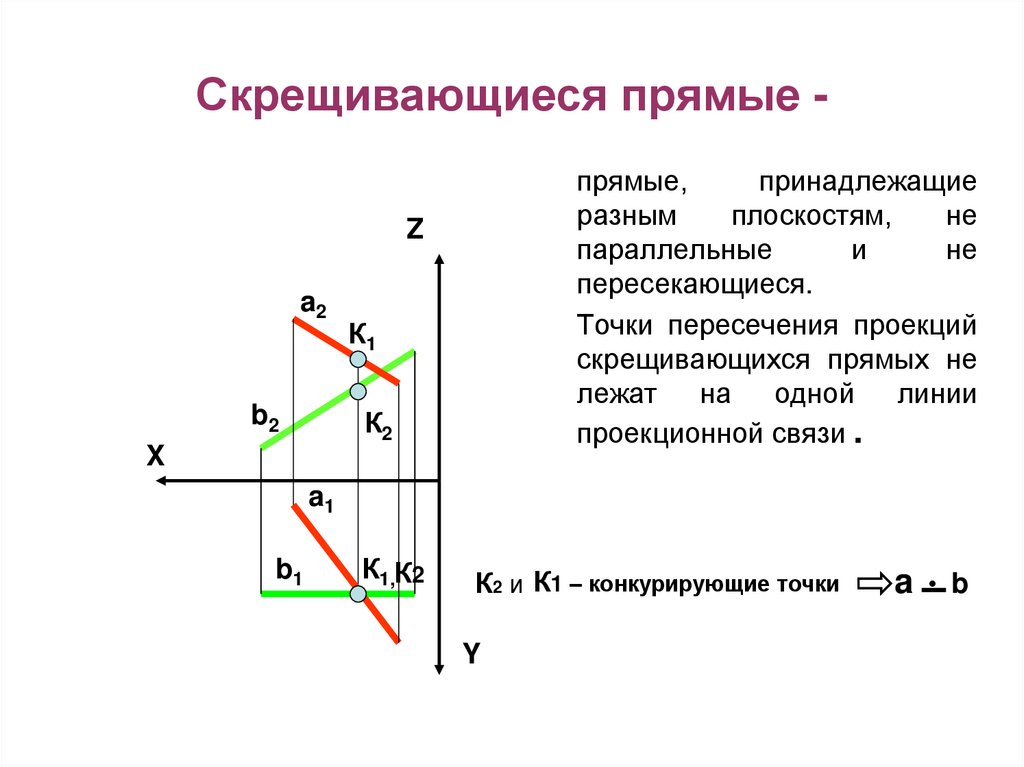
18. Скрещивающиеся прямые -

Скрещивающиеся прямые прямые,
принадлежащие
разным
плоскостям,
не
параллельные
и
не
пересекающиеся.
Точки пересечения проекций
скрещивающихся прямых не
лежат на одной линии
проекционной связи .
Z
a2
b2
К1
К2
X
a1
b1
К1,К2
К2 и К1 – конкурирующие точки
Y
a • b

19.

Видимость прямых определим по конкурирующим точкам.
(Конкурирующие точки - точки, которые на одну плоскость проецируются в
одну, а на другую – в две точки):
Конкурирующие точки располагаются дальше или ближе относительно
плоскости П2,
А2 Ξ (В2)
X
В1
А1
выше или ниже относительно плоскости П1.
С2
D2
X
D1Ξ ( C1)

20.

Определение видимости по
конкурирующим точкам
!
Из двух конкурирующих
точек видимой будет та,
которая имеет большую
координату удаления от
той плоскости проекций,
относительно которой
определяется видимость.
Наличие хотя бы одной пары конкурирующих точек
позволяет сделать однозначный вывод о скрещиваемости
прямых.

21.

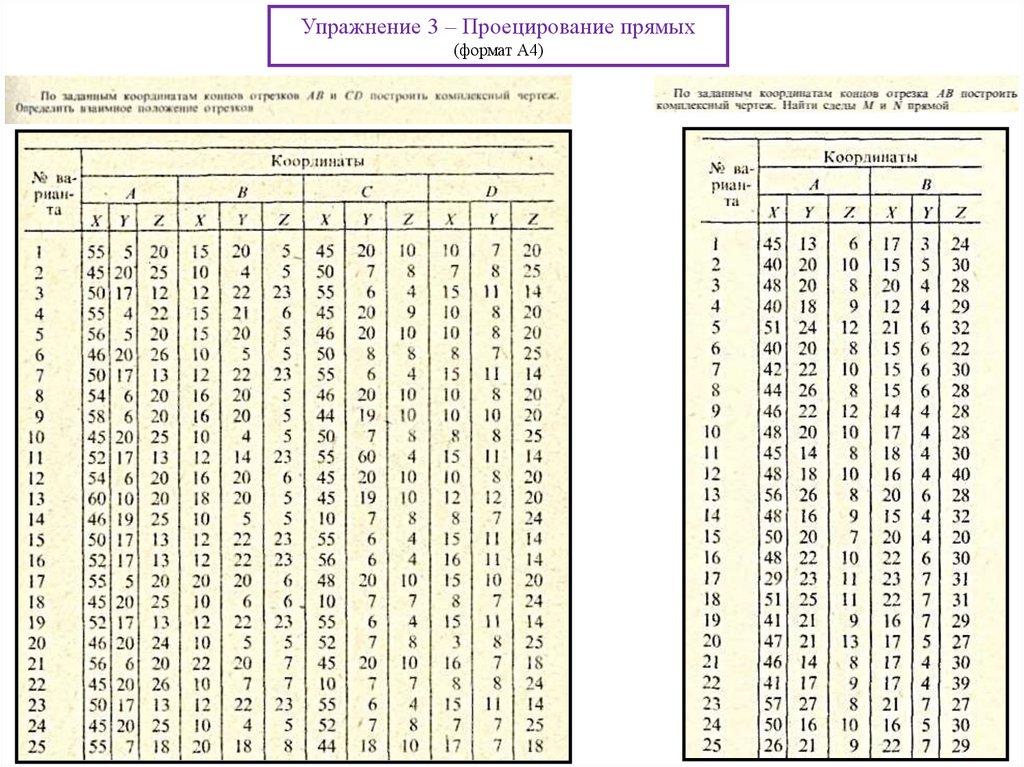
Упражнение 3 – Проецирование прямых
(формат А4)

22.

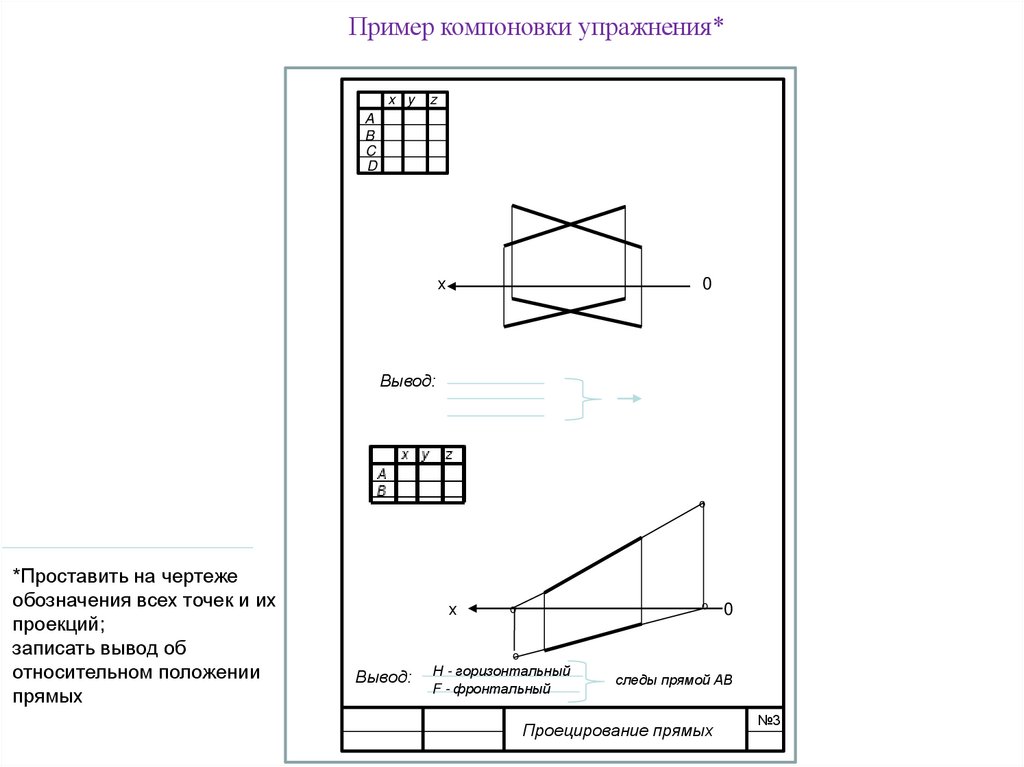
Пример компоновки упражнения*
x y
z
A
B
C
D
х
0
Вывод:
o
*Проставить на чертеже
обозначения всех точек и их
проекций;
записать вывод об
относительном положении
прямых
х
o
o
0
o
Вывод:
Н - горизонтальный
F - фронтальный
следы прямой АВ
Проецирование прямых
№3