Лекция 2 Прямая

1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Лекция 2. Прямая

Назарова Жанна Анатольевна,
доцент каф. «ПиЭА», канд. пед. наук
1

2. Лекция 2. Ортогональные проекции прямой линии

• Способы задания прямой линии
• Прямые общего положения
• Прямые частного положения
• Метод прямоугольного треугольника
• Взаимное положение двух прямых
• Свойство проекций прямого плоского
угла
2

3. Прямая линия – кратчайшее расстояние между двумя точками

Задание прямой линии:
1. Аналитическим способом
2. Графическими способами
3

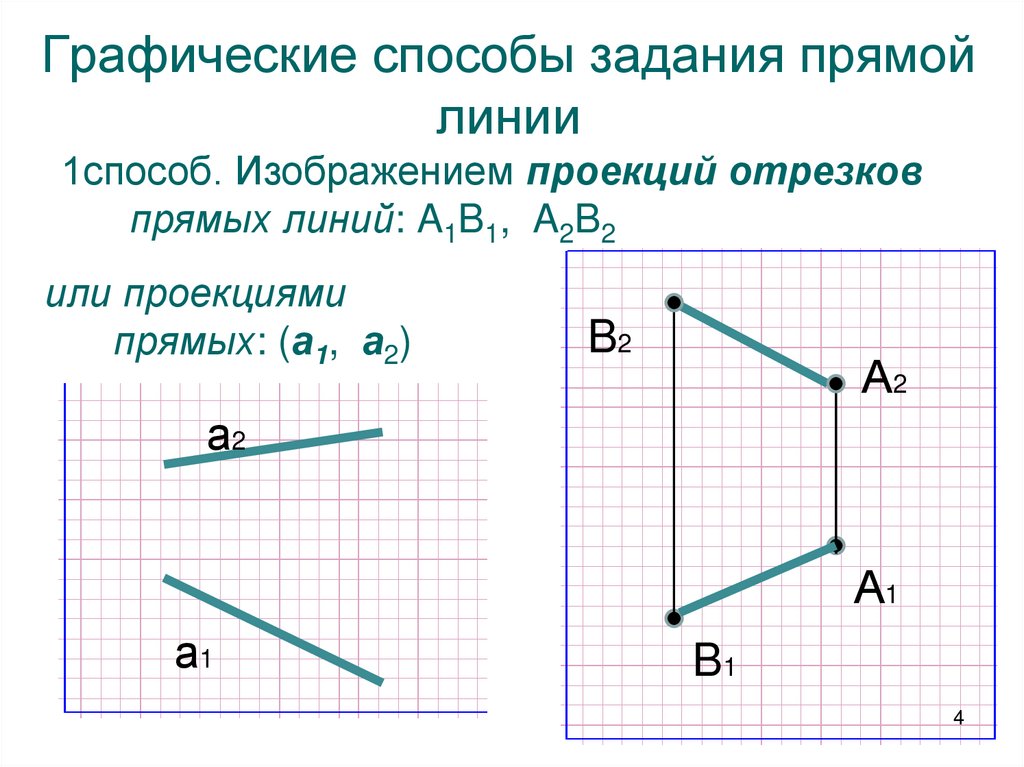
4. Графические способы задания прямой линии

1способ. Изображением проекций отрезков
прямых линий: A1B1, A2B2
или проекциями
прямых: (а1, а2)
B2
А2
а2
А1
а1
B1
4

5.

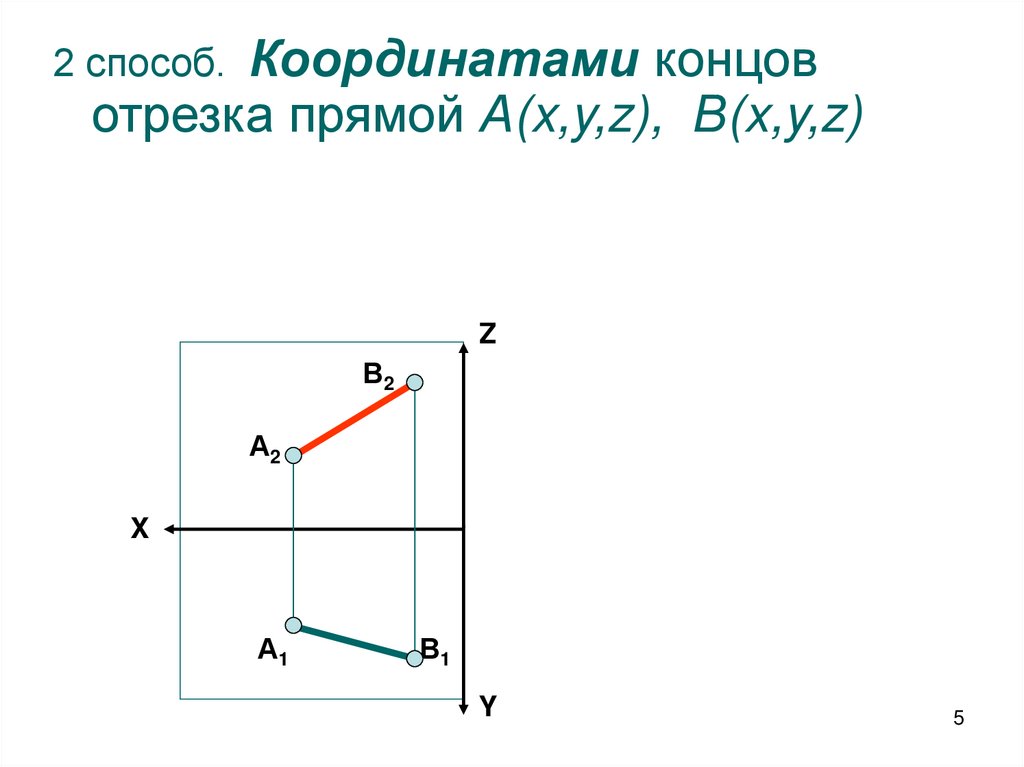
2 способ. Координатами концов
отрезка прямой А(x,y,z), В(x,y,z)
Z
В2
А2
X
А1
В1
Y
5

6.

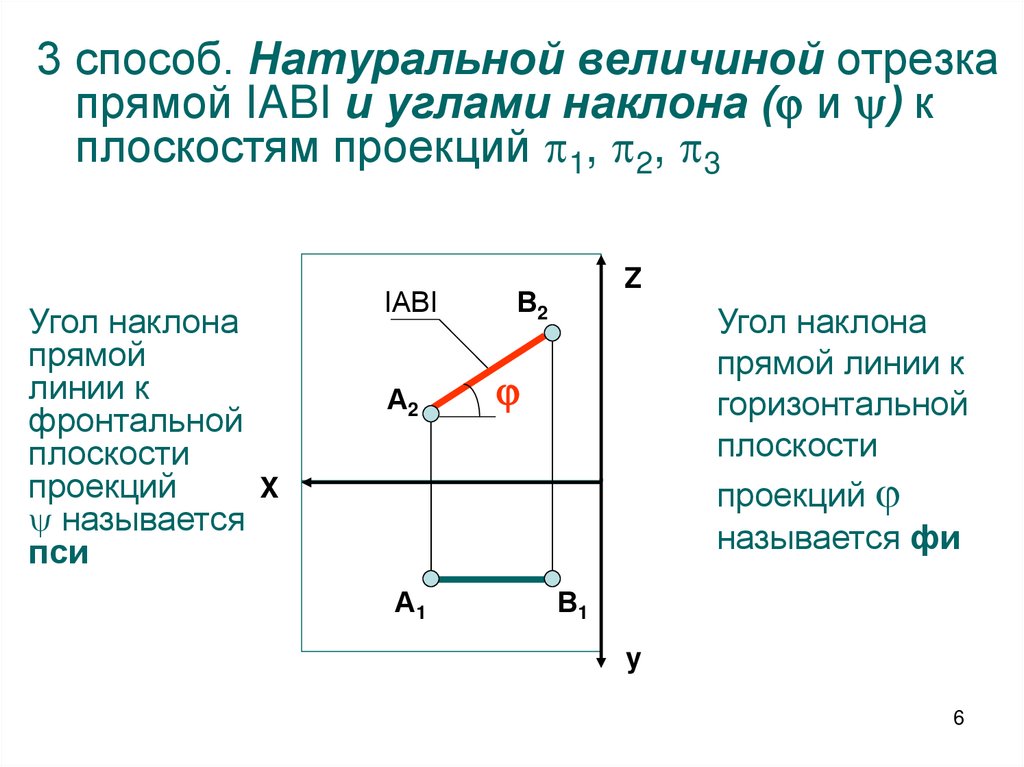
3 способ. Натуральной величиной отрезка
прямой IABI и углами наклона ( и ) к
плоскостям проекций 1, 2, 3
Угол наклона
прямой
линии к
фронтальной
плоскости
проекций
X
называется
пси
IАВI
А2
А1
Z
В2
Угол наклона
прямой линии к
горизонтальной
плоскости
проекций
называется фи
В1
y
6

7. 4 способ. Задание прямой ее следами

• Следом прямой линии
называется точка пересечения
прямой с плоскостью проекций
У прямой линии может быть три следа,
которые образуются при пересечении с
горизонтальной, фронтальной и
профильной плоскостями
7

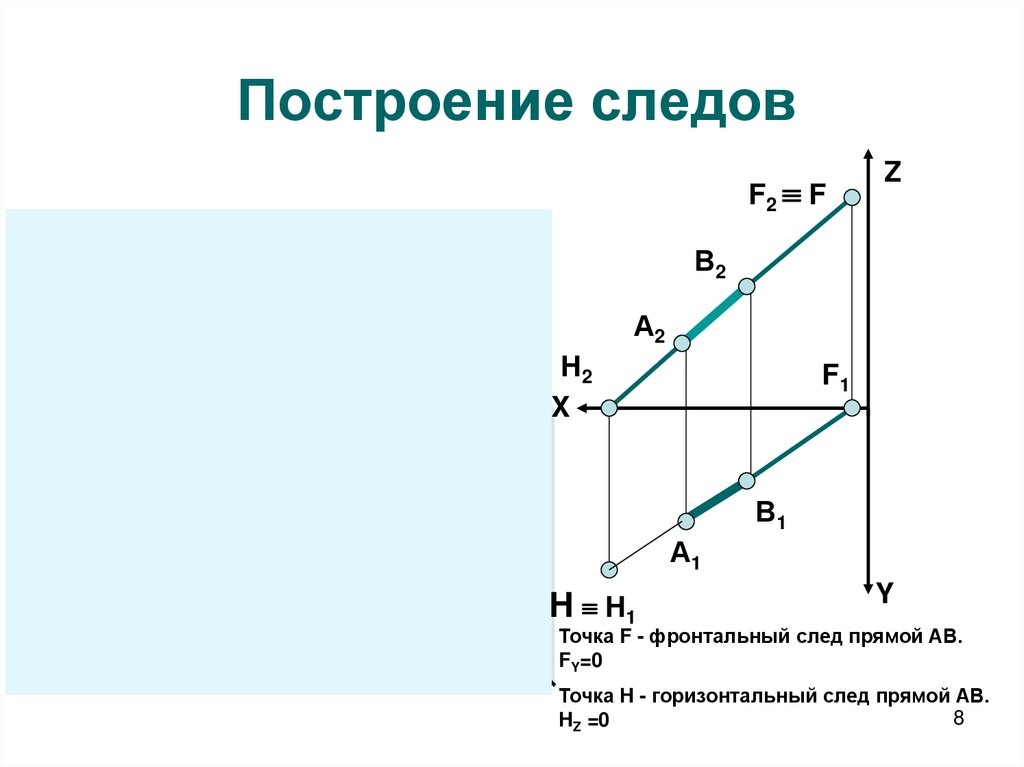
8. Построение следов

F2 F
В2
Z
2
В2
А2
H2
А2
F2 F
H2
X
F1
B
3
А
X
H1 H
Z
А1
1
В1
В1
А1
F1
H H1
Y
Y
Точка F - фронтальный след прямой АВ.
FY=0
Точка H - горизонтальный след прямой АВ.
8
HZ =0

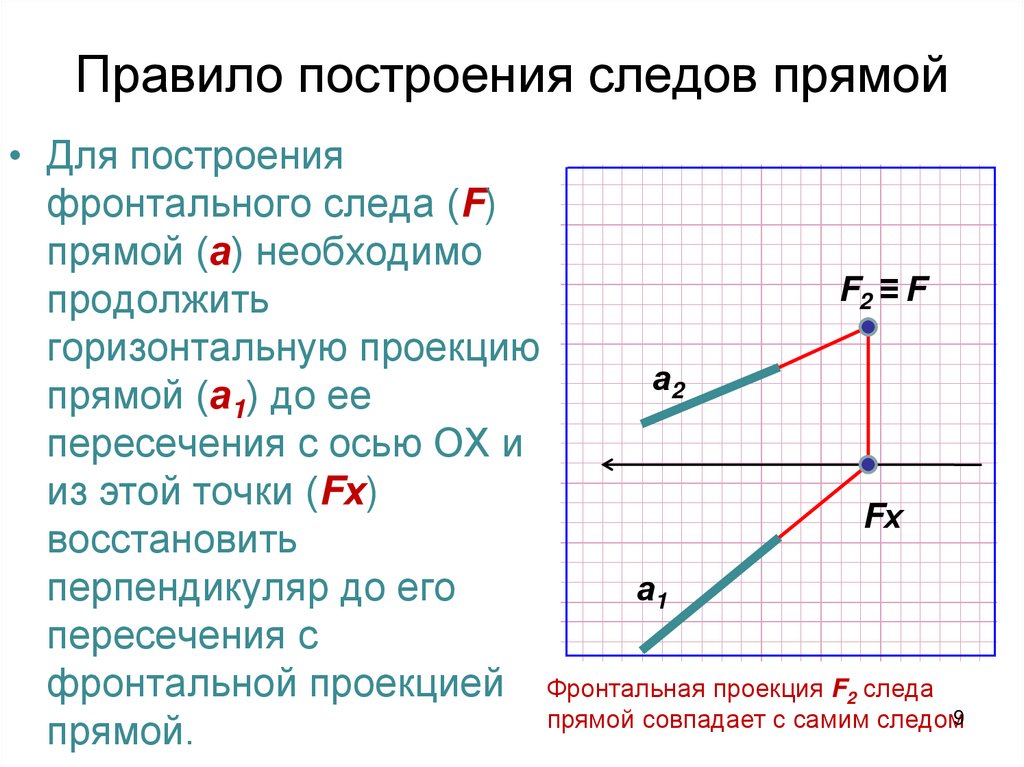
9. Правило построения следов прямой

• Для построения
фронтального следа (F)
прямой (а) необходимо
F2 ≡ F
продолжить
горизонтальную проекцию
а2
прямой (а1) до ее
пересечения с осью ОХ и
из этой точки (Fх)
Fх
восстановить
а1
перпендикуляр до его
пересечения с
фронтальной проекцией Фронтальная проекция F2 следа
прямой совпадает с самим следом9
прямой.

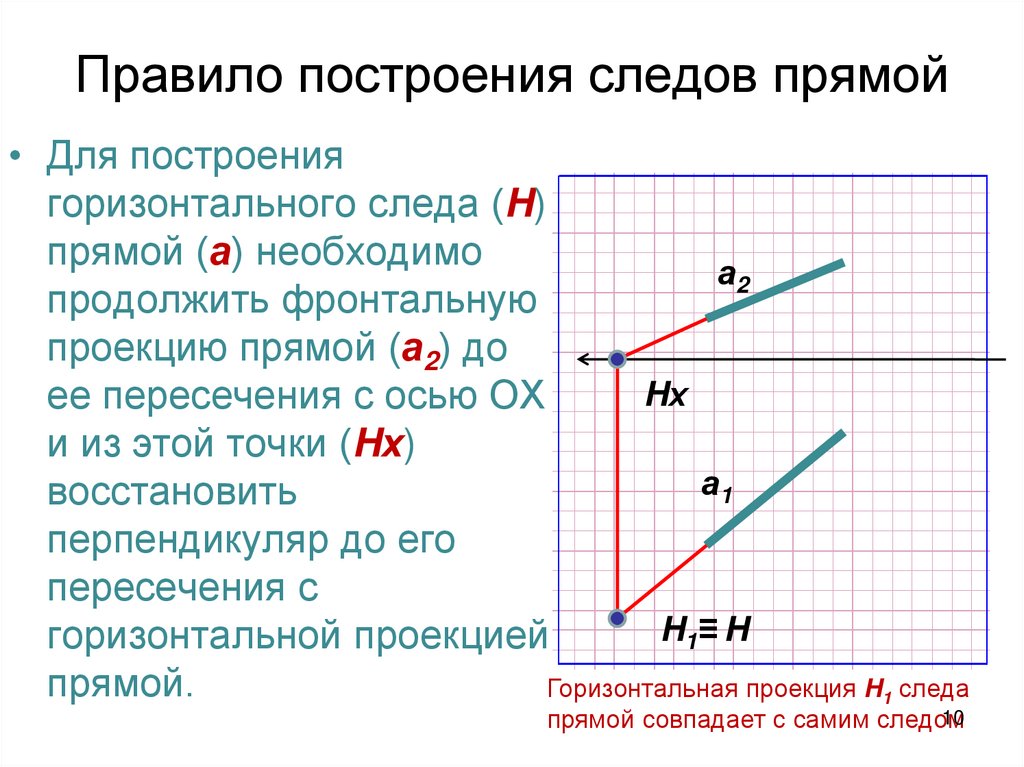
10. Правило построения следов прямой

• Для построения
горизонтального следа (H)
прямой (а) необходимо
а2
продолжить фронтальную
проекцию прямой (а2) до
Hх
ее пересечения с осью ОХ
и из этой точки (Hх)
а1
восстановить
перпендикуляр до его
пересечения с
H1≡ H
горизонтальной проекцией
прямой.
Горизонтальная проекция H1 следа
10
прямой совпадает с самим следом

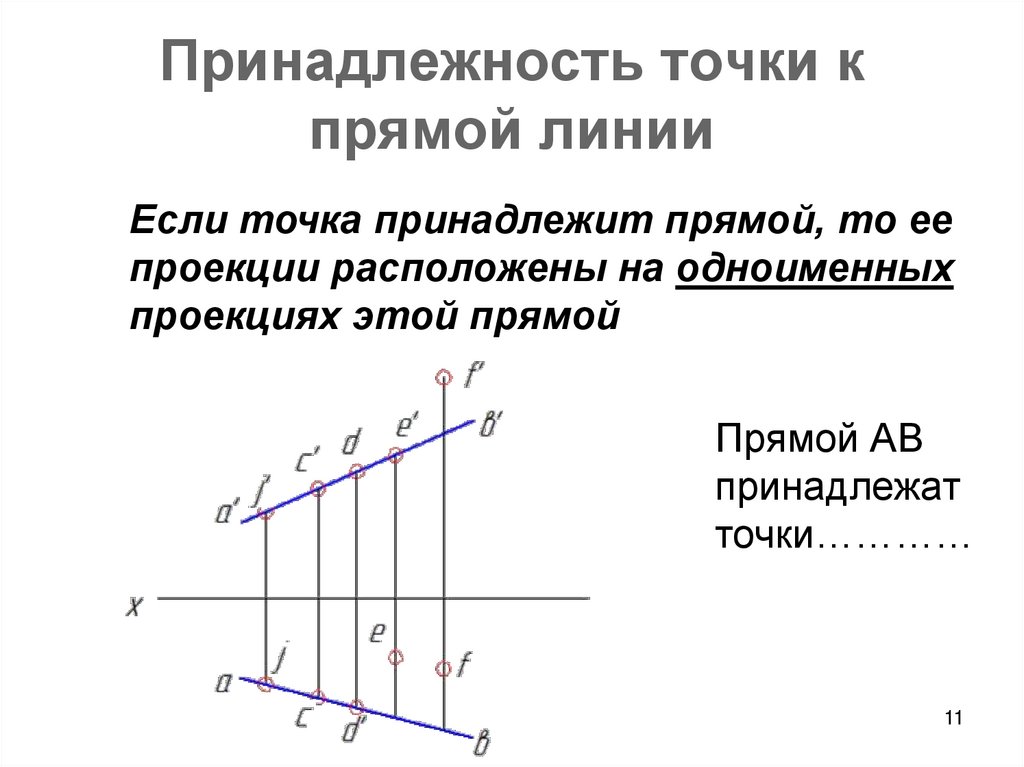
11. Принадлежность точки к прямой линии

Если точка принадлежит прямой, то ее
проекции расположены на одноименных
проекциях этой прямой
Прямой АВ
принадлежат
точки…………
11

12. Положение прямой относительно плоскостей проекций:

1. Параллельно – прямые уровня
(горизонталь, фронталь, профильная
прямая)
2. Перпендикулярно – проецирующие
прямые
3. Под углом, отличным от прямого –
прямые общего положения
12

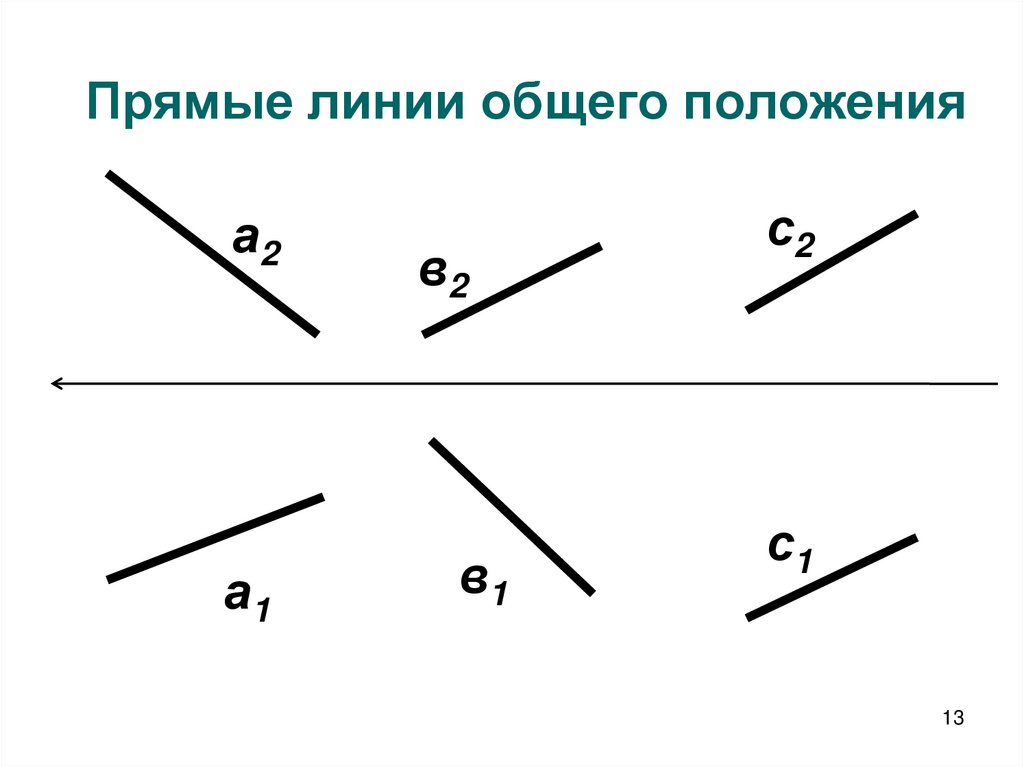
13. Прямые линии общего положения

а2
а1
в2
в1
с2
с1
13

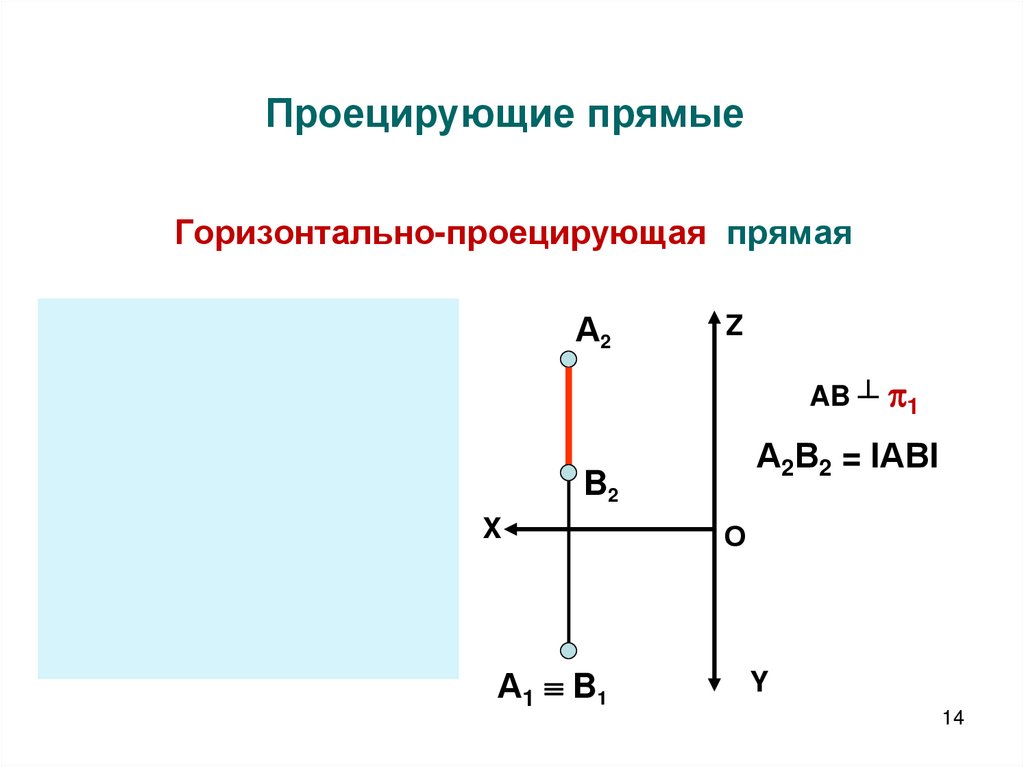
14. Проецирующие прямые

Горизонтально-проецирующая прямая
Z
А2
А2
Z
AB ┴ 1
А
B2
X
B
А2В2 = IАВI
B2
О
X
О
А1 B1
Y
А1 B1
Y
14

15.

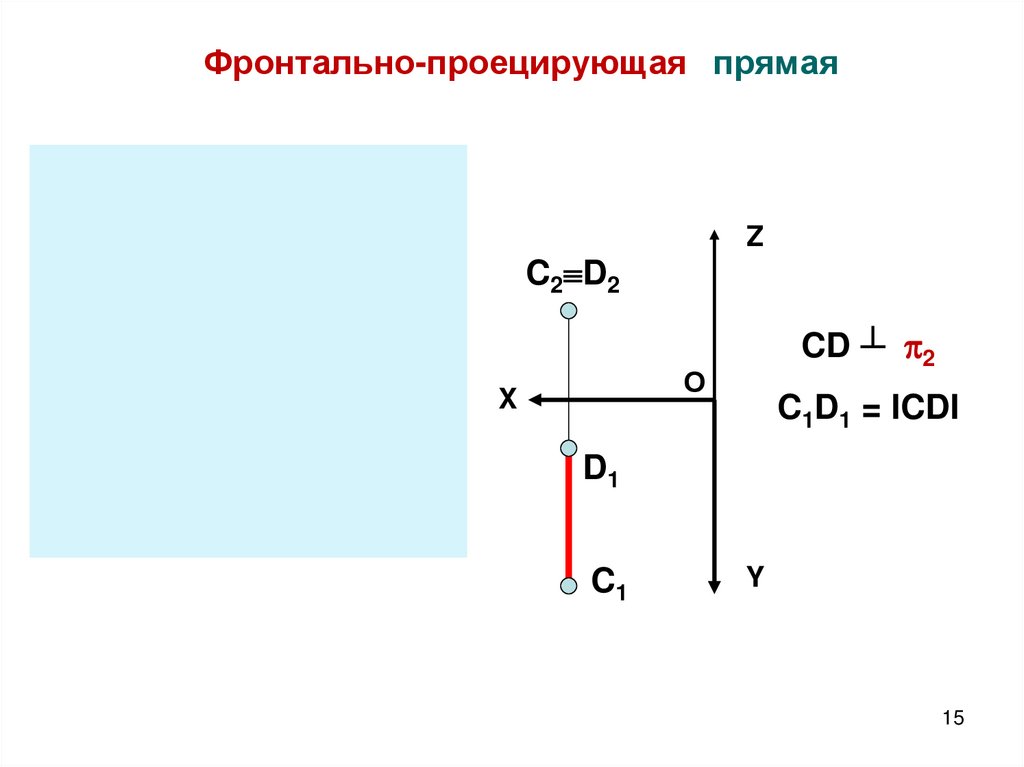
Фронтально-проецирующая прямая
Z
Z
C2 D2
C2 D2
D
C
X
О
X
D1
CD ┴ 2
C1D1 = ICDI
D1
C1
Y
C1
Y
15

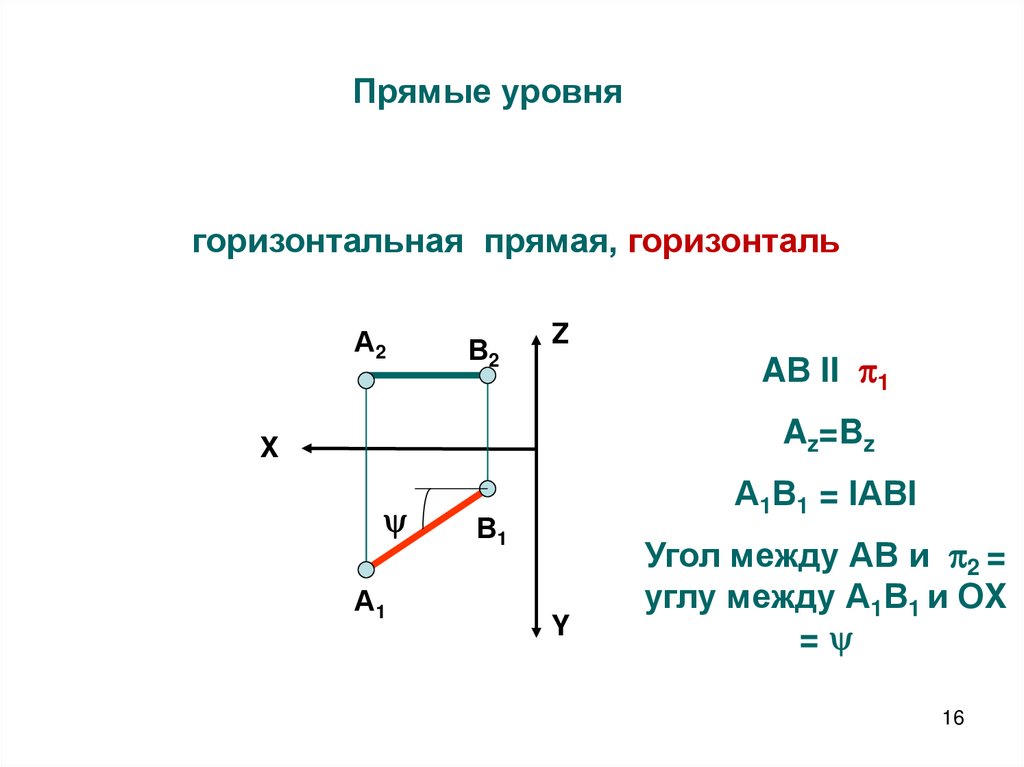
16. Прямые уровня

горизонтальная прямая, горизонталь
А2
В2
Z
AВ II 1
Az=Bz
X
А1
А1В1 = IАВI
В1
Y
Угол между АВ и 2 =
углу между А1В1 и ОX
=
16

17.

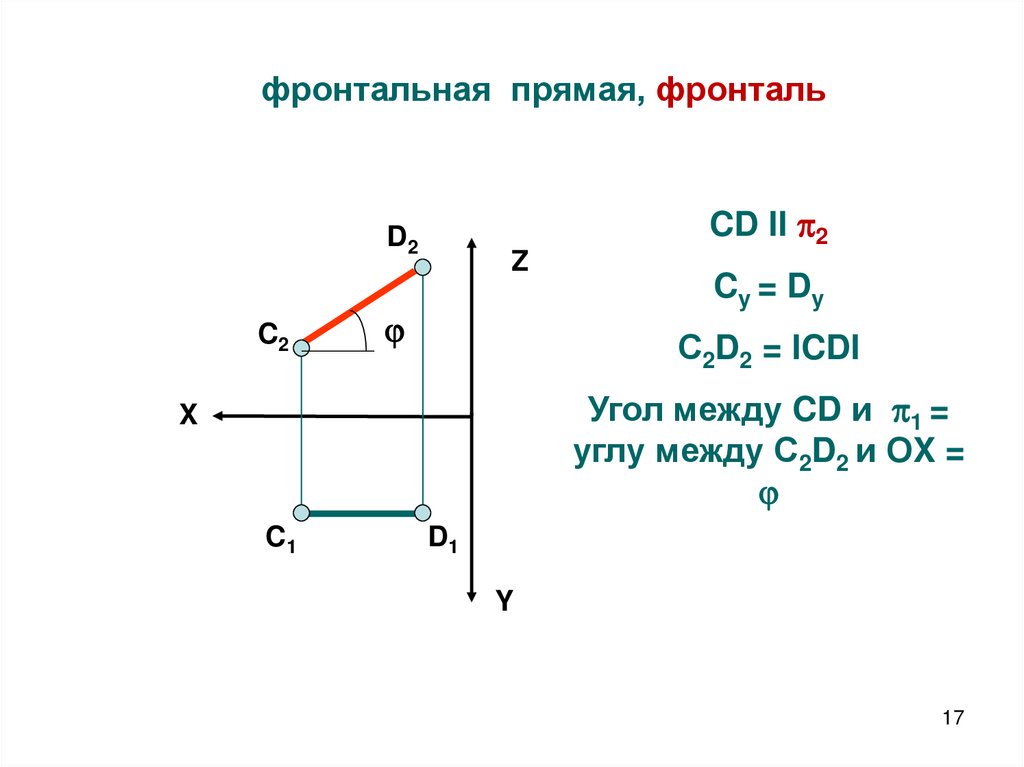
фронтальная прямая, фронталь
CD II 2
D2
C2
Z
Cy = Dy
С2D2 = ICDI
Угол между CD и 1 =
углу между С2D2 и ОX =
X
C1
D1
Y
17

18. Определение натуральной величины отрезка прямой общего положения МЕТОД ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

ДЛИНА ОТРЕЗКА РАВНА
ГИПОТЕНУЗЕ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА,
ОДИН КАТЕТ КОТОРОГО РАВЕН ПРОЕКЦИИ
ОТРЕЗКА, А ДРУГОЙ – РАЗНОСТИ КООРДИНАТ
КОНЦОВ ОТРЕЗКА ОТ ЭТОЙ ЖЕ ПЛОСКОСТИ
18

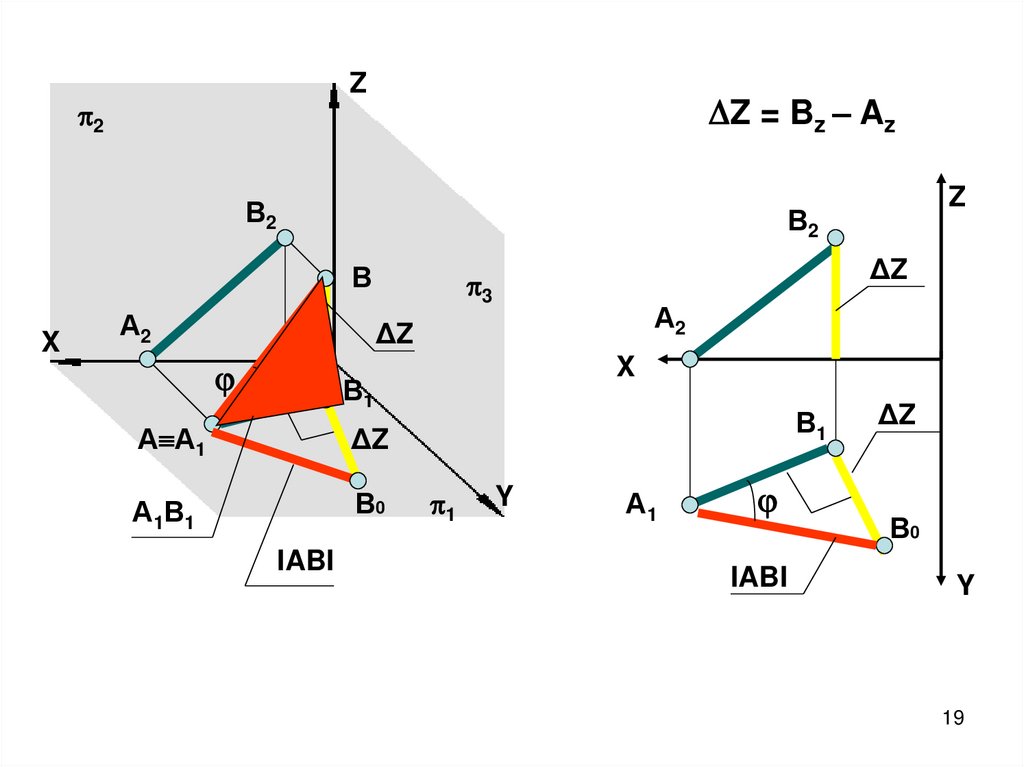
19.

Z
2
Z = Bz – Az
В2
В2
В
X
Z
А2
ΔZ
3
А2
ΔZ
X
В1
А А1
ΔZ
А1В1
В0
IABI
В1
1
Y
А1
IABI
ΔZ
В0
Y
19

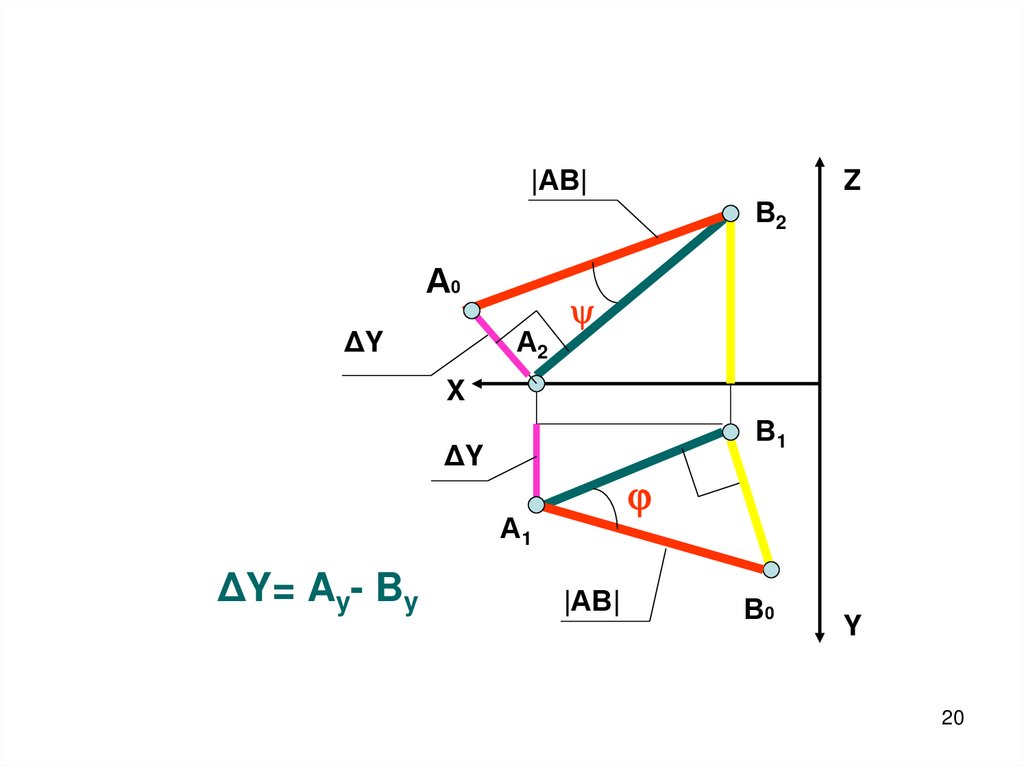
20.

|АВ|
Z
В2
А0
ΔY
А2
X
В1
ΔY
А1
ΔY= Ay- By
|АВ|
В0
Y
20

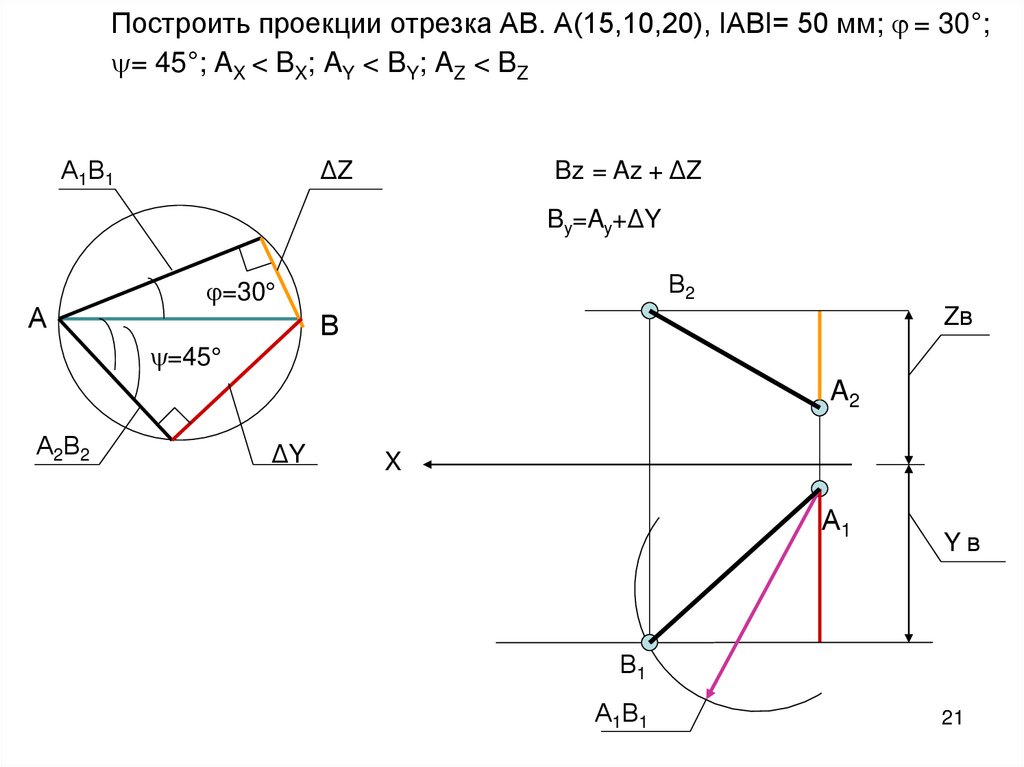
21.

Построить проекции отрезка АВ. А(15,10,20), IАВI= 50 мм; = 30°;
= 45°; AX < BX; AY < BY; AZ < BZ
А1В1
ΔZ
Bz = Az + ΔZ
By=Ay+ΔY
А
В2
=30
Zв
В
=45
A2
А2В2
ΔY
X
А1
Yв
В1
А1В1
21

22. Относительное положение прямых

Прямые в пространстве могут быть расположены:
1. Параллельно
2. Перпендикулярно
3. Пересекаться
4. Скрещиваться
22

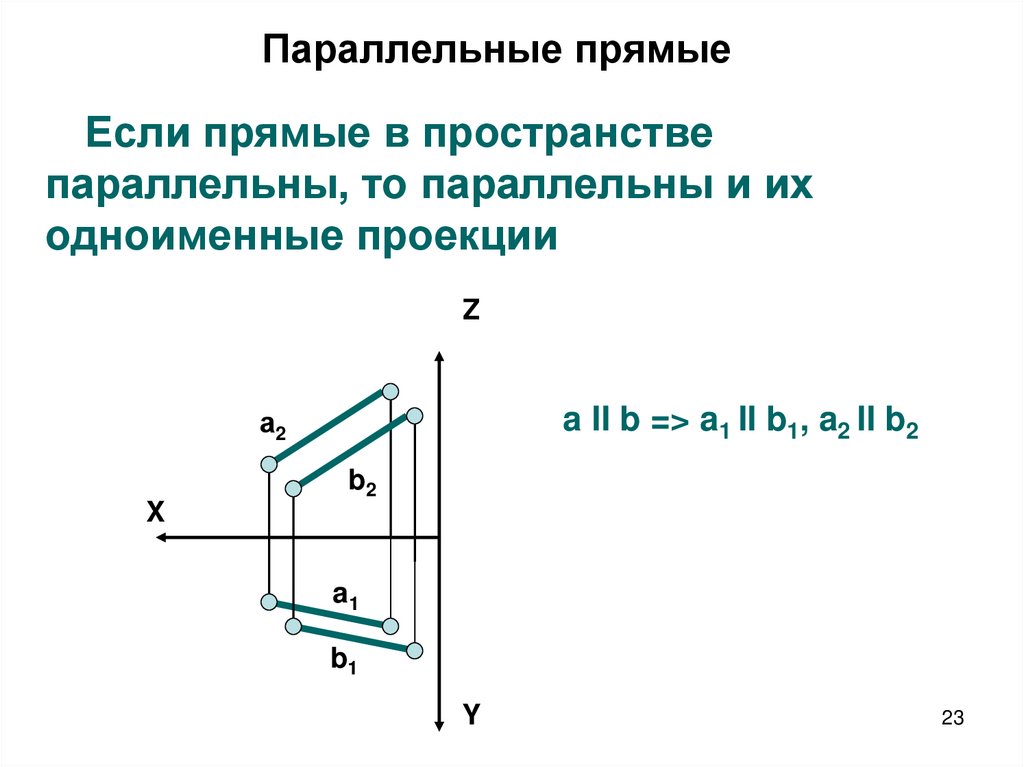
23. Параллельные прямые

Если прямые в пространстве
параллельны, то параллельны и их
одноименные проекции
Z
a II b => a1 II b1, a2 II b2
а2
b2
X
a1
b1
Y
23

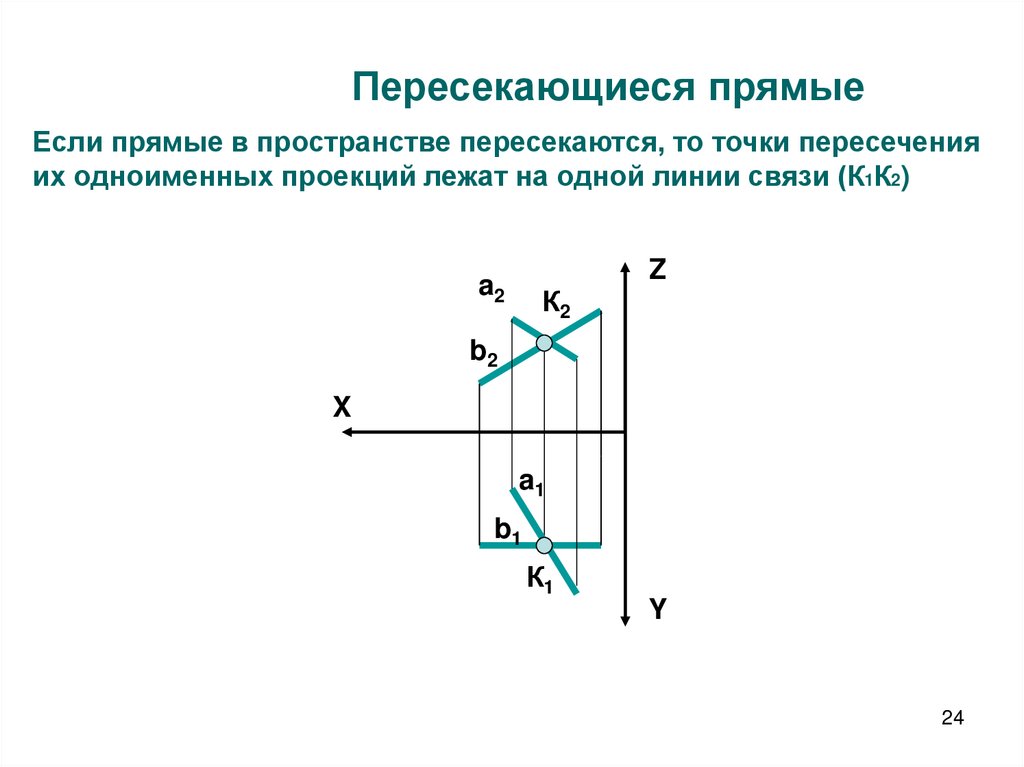
24. Пересекающиеся прямые

Если прямые в пространстве пересекаются, то точки пересечения
их одноименных проекций лежат на одной линии связи (К1К2)
Z
a2
К2
b2
X
a1
b1
К1
Y
24

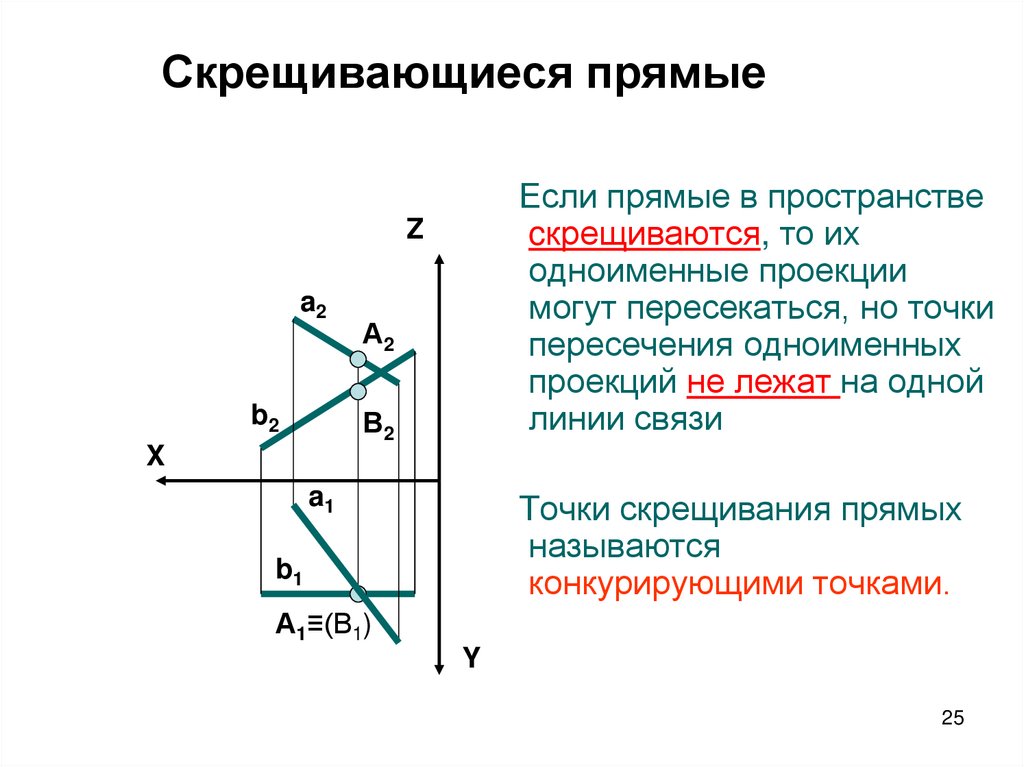
25. Скрещивающиеся прямые

Если прямые в пространстве
cкрещиваются, то их
одноименные проекции
могут пересекаться, но точки
пересечения одноименных
проекций не лежат на одной
линии связи
Z
a2
b2
А2
В2
X
a1
Точки скрещивания прямых
называются
конкурирующими точками.
b1
А1≡(В1)
Y
25

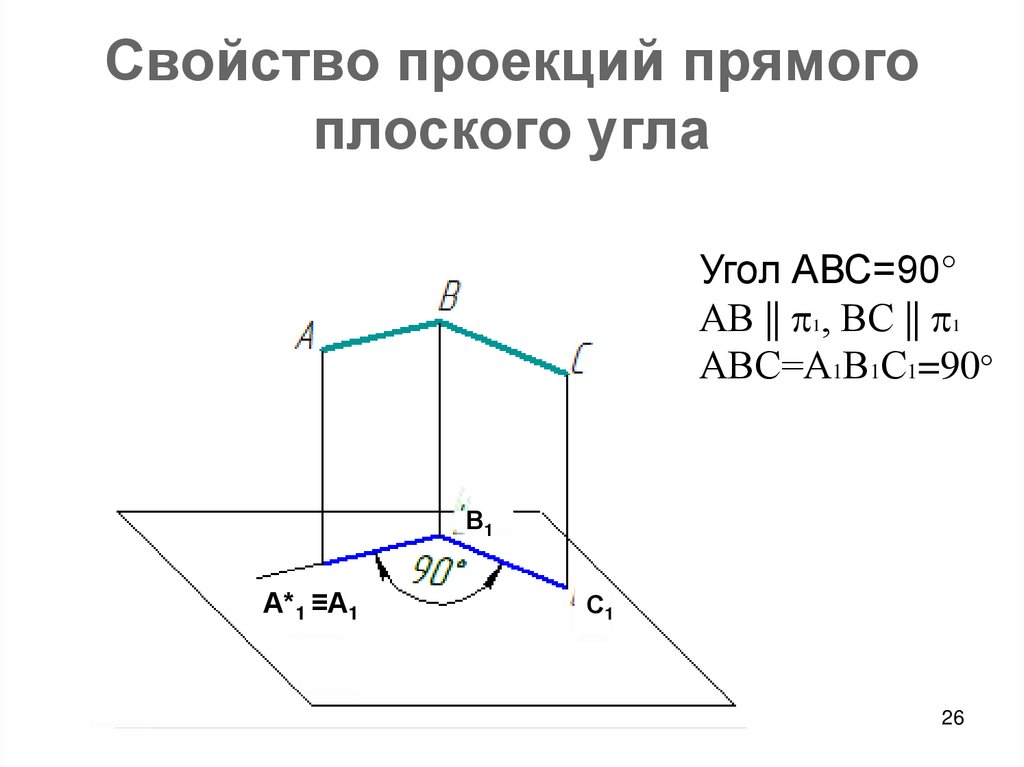
26. Свойство проекций прямого плоского угла

Угол АВС=90°
АВ || 1, ВС || 1
АВС=А1В1С1=90°
В1
А*1 ≡А1
С1
26

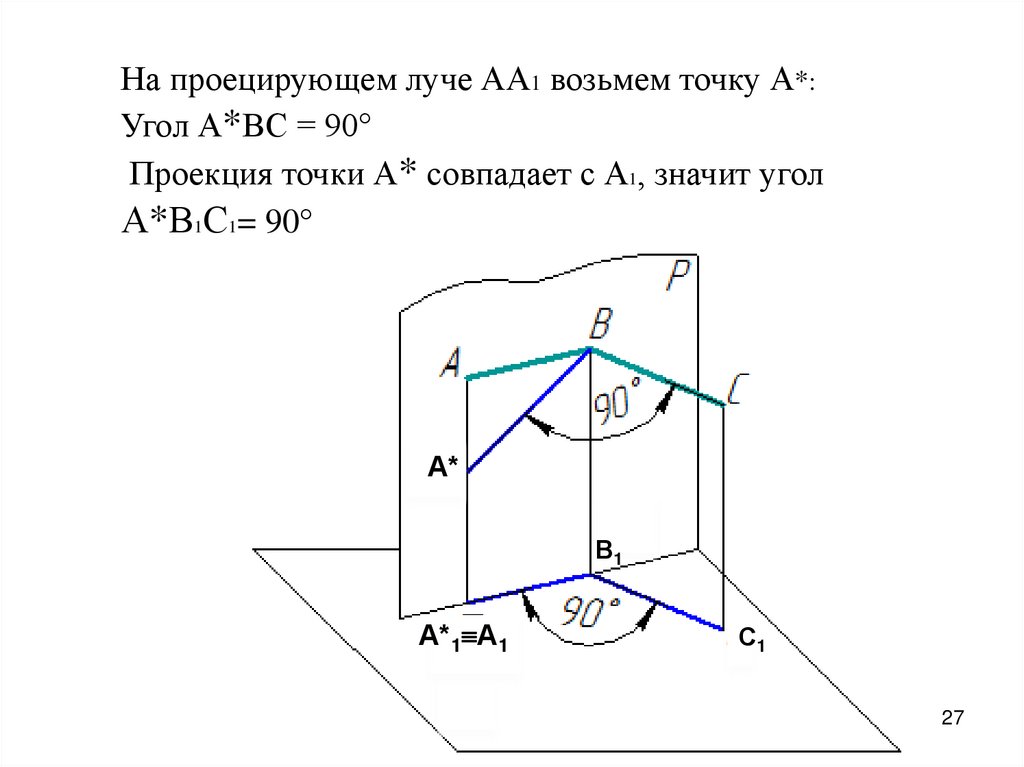
27.

На проецирующем луче АА1 возьмем точку А*:
Угол А*ВС = 90°
Проекция точки А* совпадает с А1, значит угол
А*В1С1= 90°
А*
В1
А*1 А1
С1
27

28. Свойство проекций прямого плоского угла

Если одна сторона прямого плоского
угла параллельна плоскости
проекций, то прямой угол на эту
плоскость проецируется в
натуральную величину
28

29. Спасибо за внимание!

29